将phantomjs制成docker镜像
几个前的一篇文章中介绍了phantomjs+echarts生成图表图片的一种方式,但其部署复杂,制作为docker镜像运行就方便多了。文章参见:https://blog.csdn.net/u011943534/article/details/121524397
1、准备echarts
将上次文章中提到过下载的EchartsConvert 解压,并复制到一个安装docker的服务器。
下载地址:https://gitee.com/saintlee/echartsconvert
2、准备phantomjs
将上次文章中个体到过下载的phantomjs解压,并复制bin目录下的phantomjs文件到上一步和echarts相同的目录
下载地址:https://bitbucket.org/ariya/phantomjs/downloads/
注意下载linux版本的
3、编写dockerfile
FROM debian:stable-slim
RUN apt-get update
RUN apt-get install -y apt-transport-https ca-certificates#mirror
COPY sources.list /etc/apt/sources.list#phantomjs
RUN apt-get update
RUN apt-get install -y libfontconfig1
ENV OPENSSL_CONF /etc/ssl/
COPY phantomjs /usr/local/bin
RUN chmod +x /usr/local/bin/phantomjs
ADD echartsconvert-master /echartsconvert-master
RUN apt-get install -y ttf-wqy-zenhei
RUN apt-get install -y xfonts-intl-chinese wqy*
RUN cp /usr/share/zoneinfo/Asia/Shanghai /etc/localtimeEXPOSE 7777
CMD ["/usr/local/bin/phantomjs", "/echartsconvert-master/echarts-convert.js", "-s", "-p", "7777"]其中sources.list如下:
deb https://mirrors.tencent.com/debian/ bullseye main non-free contrib
deb-src https://mirrors.tencent.com/debian/ bullseye main non-free contrib
deb https://mirrors.tencent.com/debian-security/ bullseye-security main
deb-src https://mirrors.tencent.com/debian-security/ bullseye-security main
deb https://mirrors.tencent.com/debian/ bullseye-updates main non-free contrib
deb-src https://mirrors.tencent.com/debian/ bullseye-updates main non-free contrib
deb https://mirrors.tencent.com/debian/ bullseye-backports main non-free contrib
deb-src https://mirrors.tencent.com/debian/ bullseye-backports main non-free contrib
4、构建镜像
docker build -t phantomjs:0.0.1 .
5、运行镜像
docker run -d --name=phantomjs --restart=always -p 7777:7777 phantomjs:0.0.1
相关文章:

将phantomjs制成docker镜像
几个前的一篇文章中介绍了phantomjsecharts生成图表图片的一种方式,但其部署复杂,制作为docker镜像运行就方便多了。文章参见:https://blog.csdn.net/u011943534/article/details/121524397 1、准备echarts 将上次文章中提到过下载的Echart…...

【LeetCode+JavaGuide打卡】Day20|530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先
学习目标: 530.二叉搜索树的最小绝对差 501.二叉搜索树中的众数 236. 二叉树的最近公共祖先 学习内容: 530.二叉搜索树的最小绝对差 题目链接&&文章讲解 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值…...

【工具类】开源照片管理工具pthtoprism
1. pthtoprism 1. pthtoprism 1.1. 安装1.2. 管理照片方式 1.2.1. 直接管理原始照片目录1.2.2. 导入照片 1.3. 界面功能1.4. 参考资料 1.1. 安装 wget https://dl.photoprism.app/docker/docker-compose.yml # 修改 docker-compose.yml 文件,具体参考下面内容 d…...

[ linux网络 ] 网关服务器搭建,综合应用SNAT、DNAT转换,dhcp分配、dns分离解析,nfs网络共享以及ssh免密登录
实验准备工作: 网关服务器安装:dhcp bind (yum install -y dhcp bind bind-utlis) server1安装:httpd (yum install -y httpd) 没有网络就搭建本地yum仓库或者配置网卡使其能够上网。 ( 1)网关服务器…...

MySQL全量备份
一、实验素材 1.创建student和score表 (1) student表 create database school; use schoolCREATE TABLE student ( id INT(10) NOT NULL UNIQUE PRIMARY KEY , name VARCHAR(20) NOT NULL , sex VARCHAR(4) , birth YEAR, department VARCHAR(20) , address VARCHAR(50) );(…...
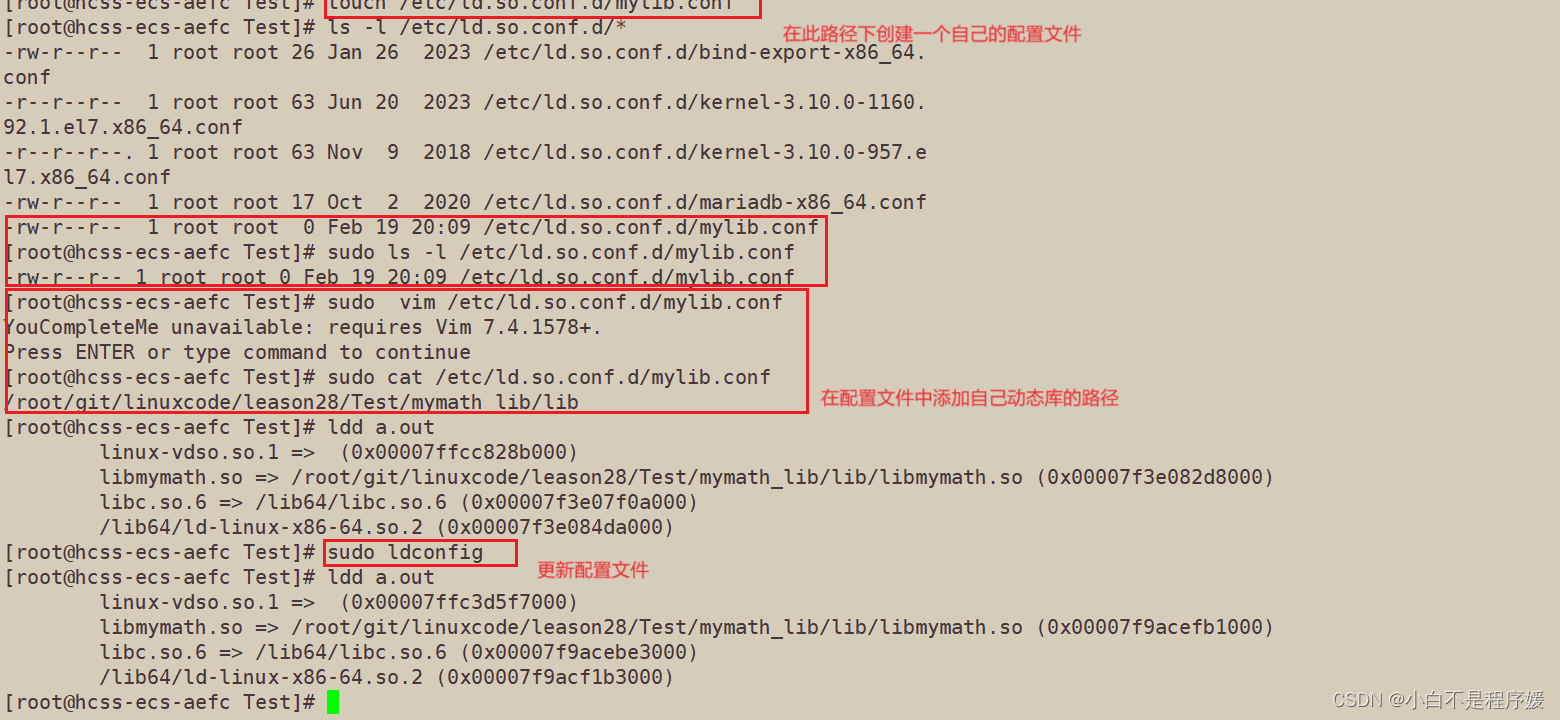
【Linux系统化学习】动静态库 | 软硬链接
目录 硬链接和软链接 硬链接 软链接 动态库和静态库 静态库 静态库的生成 静态库的使用 将库打包和使用 动态库 动态库的生成 动态库的使用 库搜索路径 硬链接和软链接 硬链接 上篇文章我们说到真正找到磁盘上的文件并不是文件名,而是inode。其实在…...

linux-firewalld防火墙端口转发
目的:通过统一地址实现对外同一地址暴露 1.系统配置文件开启 ipv4 端口转发 echo "net.ipv4.ip_forward 1" >> /etc/sysctl.confsysctl -p 2.查看防火墙配置端口转发之前的状态 firewall-cmd --statefirewall-cmd --list-all 3.开启 IP 伪装 firewall-cm…...
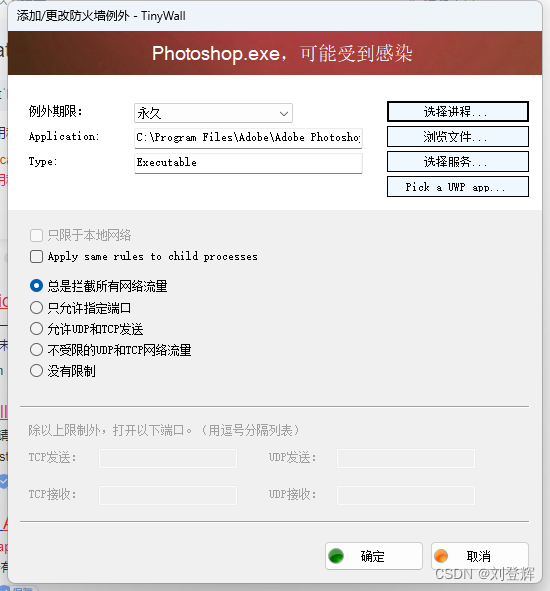
adobe软件提示This non-genuine Adobe app will be disabled soon【软件版本】
因为电脑上级路由器装了小飞机,导致本机电脑ps等adobe的系列软件出现了 This non-genuine Adobe app will be disabled soon,烦人的狠,之前有写过一篇通过更改host的教程,现在已经失效了,今天为大家分享一个用软件来屏…...

python coding with ChatGPT 打卡第20天| 二叉搜索树:搜索、验证、最小绝对差、众数
相关推荐 python coding with ChatGPT 打卡第12天| 二叉树:理论基础 python coding with ChatGPT 打卡第13天| 二叉树的深度优先遍历 python coding with ChatGPT 打卡第14天| 二叉树的广度优先遍历 python coding with ChatGPT 打卡第15天| 二叉树:翻转…...

Stable Diffusion——基础模型、VAE、LORA、Embedding各个模型的介绍与使用方法
前言 Stable Diffusion(稳定扩散)是一种生成模型,基于扩散过程来生成高质量的图像。它通过一个渐进过程,从一个简单的噪声开始,逐步转变成目标图像,生成高保真度的图像。这个模型的基础版本是基于扩散过程…...

Python自动化部署与配置管理:Ansible与Docker
Ansible 和 Docker 是两种常用于自动化部署和配置管理的工具。Ansible 是一个基于 Python 的自动化运维工具,可以配置管理、应用部署、任务自动化等。而 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中&…...

《摔跤吧爸爸》19岁女星突患皮肌炎离世
从确诊到离世仅10天……罕见病“皮肌炎”! 曾凭借在知名电影《摔跤吧!爸爸》中饰演童年时期“小芭比塔”一角而广受喜爱的年轻演员苏哈尼巴特纳格尔不幸离世,年仅19岁。她的突然逝世引发了全球关注,据苏哈妮的家人表示࿰…...

用结构体数组,完成宠物信息登记管理。
管理宠物的名字,品种,年龄。 实现功能如下: 1.插入宠物信息 2.遍历宠物信息 #include <stdio.h> #define N 100 typedef struct chongwu { char name[20]; char pingz[10]; int age; }cw; void intset_cw(cw *ptr,int *pnum) { printf("请…...

频率主义线性回归和贝叶斯线性回归
整体概述 频率主义(Frequentist)线性回归和贝叶斯(Bayesian)线性回归是统计学中用于数据分析和预测的两种主要方法,特别是在建模关于因变量和自变量之间线性关系的上下文中。尽管两种方法都用于线性回归分析ÿ…...
)
【感知算法】Dempster-Shafer理论(下)
尝试DS理论应用到自动驾驶地图众包更新。 地图特征变化判断 a mass function is applied to quantify the evidence of the existence. existence state: existenct、non-existent、tenative、conflict ∃ ∄ Ω ϕ \exist \\ \not\exist \\ \Omega \\ \phi ∃∃Ωϕ ma…...

通过conda安装cudatoolikit和cudnn
通过conda安装cudatoolikit和cudnn 安装cudatoolkit安装cudnn安装cudatoolkit-dev 安装cudatoolkit conda install cudatoolkit11.3 -c https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ 安装cudnn conda install cudnn8.5 -c https://mirrors.tuna.tsinghua.edu.…...

vue中使用jsx语法
请注意,在 Vue 中使用 JSX 时,你仍然需要通过 h 函数(通常是一个别名,对应于 createElement 函数)来创建虚拟 DOM 元素。在下面的例子中,h 函数作为 render 函数的参数传入,但在 JSX 语法中你通…...
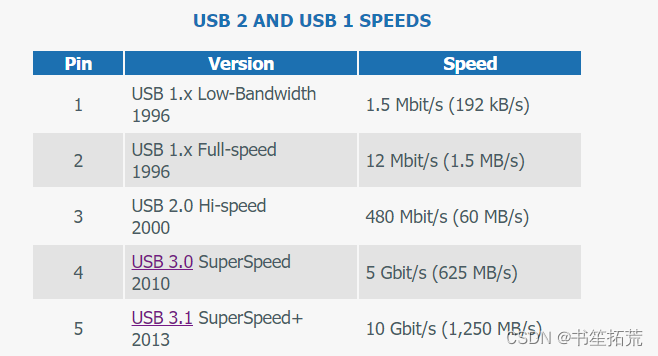
我的NPI项目之Android USB 系列(一) - 遥望和USB的相识
和USB应该是老朋友了,从2011年接触Android开发开始,就天天和USB打交道了。那时候还有不 对称扁头的usb/方口的usb,直到如今使用广泛的防反插USB3.0 type-C。 但是,一直有一个不是很清楚的问题萦绕在心头,那就是。先有…...
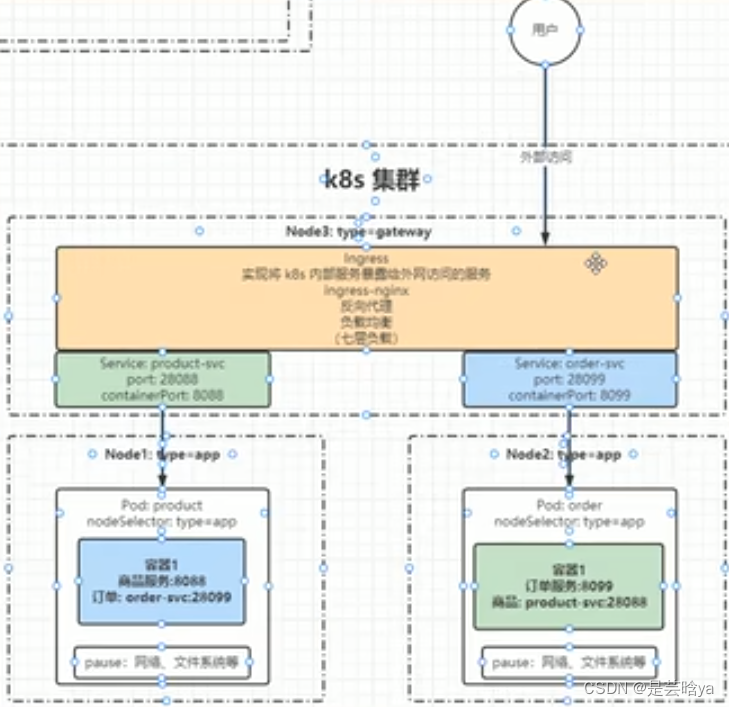
K8s进阶之路-命名空间级-服务发现 :
服务发现: Service(东西流量):集群内网络通信、负载均衡(四层负载)内部跨节点,节点与节点之间的通信,以及pod与pod之间的通信,用Service暴露端口即可实现 Ingress&#…...

智慧公厕管理系统:让城市智慧驿站更加智慧舒适
智慧公厕管理系统是城市智慧驿站中不可或缺的一部分,它通过全方位的信息化解决方案,为公共厕所的使用、运营和管理提供了一种智能化的方式。作为城市智慧驿站的重要组成部分,智慧公厕管理系统发挥着重要的作用,为城市社会民生提供…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
