面试经典150题——单词规律

"Don't wait. The time will never be just right." - Napoleon Hill

1. 题目描述

2.  题目分析与解析

首先还是得把题目先读懂，我们直接来看看示例：

根据上面的示例，我们可以看出pattern其实就是表示单词出现的规律，每一种pattern中的字符表示一个单词。

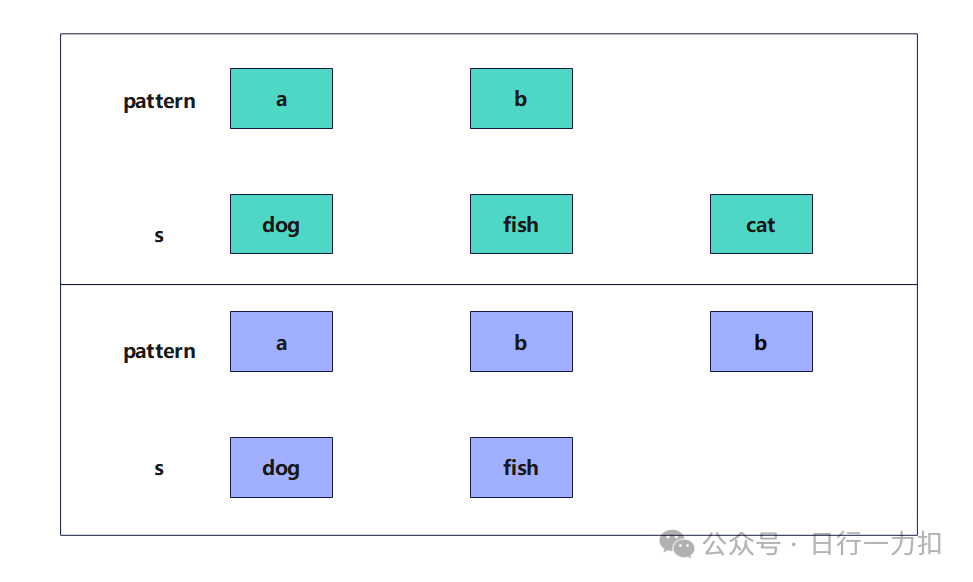
就比如上面的示例一：

pattern="abba"，对应于s，就可以发现 a = dog， b = cat，这样pattern（abba）实际上就是对应了

(a=)dog(b=)cat(b=)cat(a=)dog

而这种映射关系是不可更改的，比如看示例二，开始a对应dog，b对应cat，但是当我们走到pattern的最后一个字符发现a等于 fish，而之前我们已经将 a=dog，所以此时映射失败就返回false。

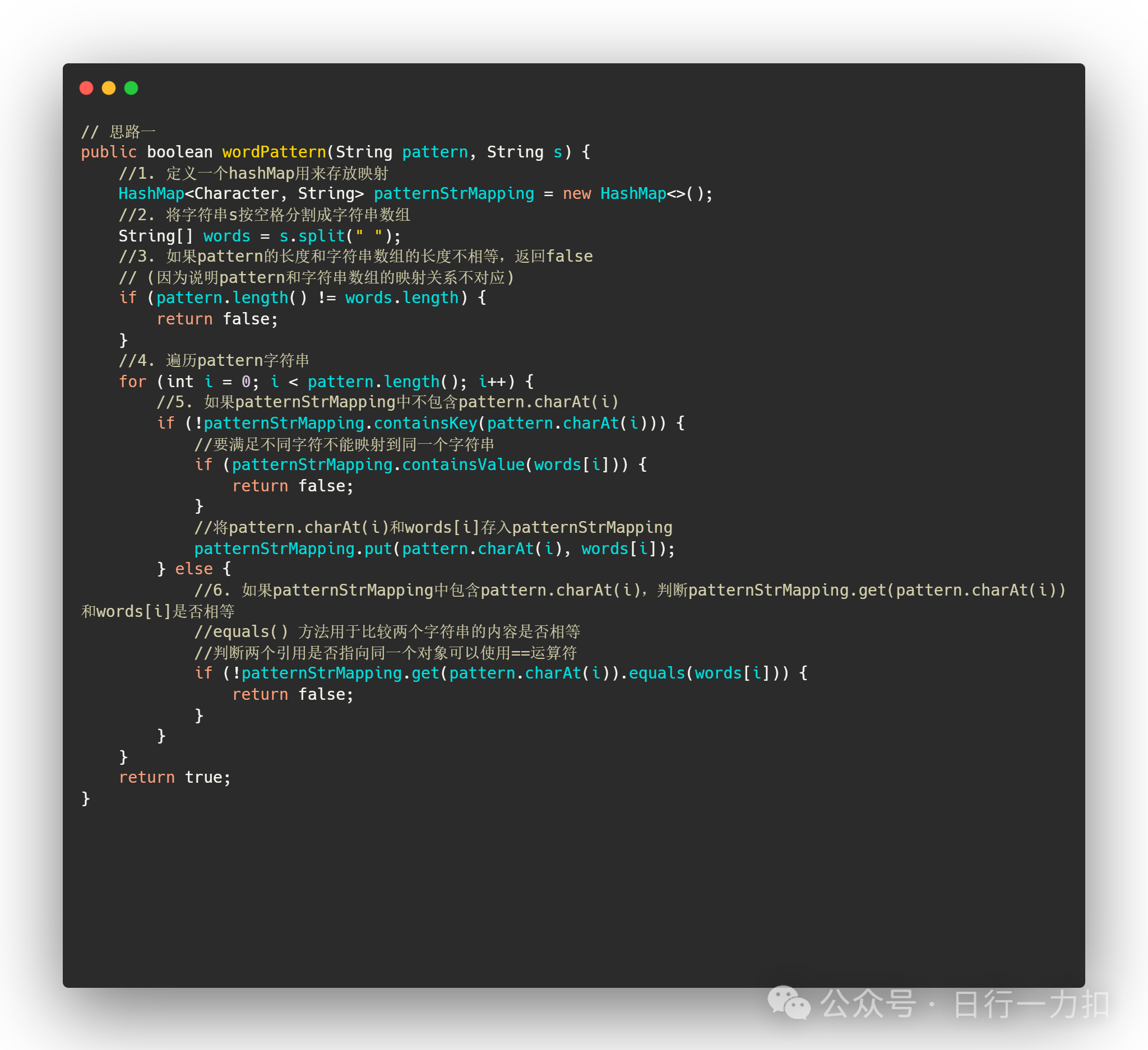
2.1 思路一——hash映射表

根据上面的读题以及上一篇文章，我想大家应该能很快想出来其实还是映射关系，映射怎么办？那就用一个hashMap解决呗。尝试将pattern中的字符不断向映射表中存放，其实和上一篇文章基本数一摸一样，

• 当发现pattern中某一个字符在映射表中不存在，就将该字符作为键，对应的s中的单词作为值，放入映射表。

• 当发现pattern中某一个字符在映射表中存在，查看对应的值是否与s中对应位置的单词匹配，匹配成功继续匹配，匹配失败则返回false。

• 当走完整个pattern，都没返回false，那么就说明映射成功！

• 但是我们需要先把s字符串按照空格切割成单词

  //2. 将字符串s按空格分割成字符串数组String[] words = s.split(" ");

这就造成了大量的额外空间的浪。

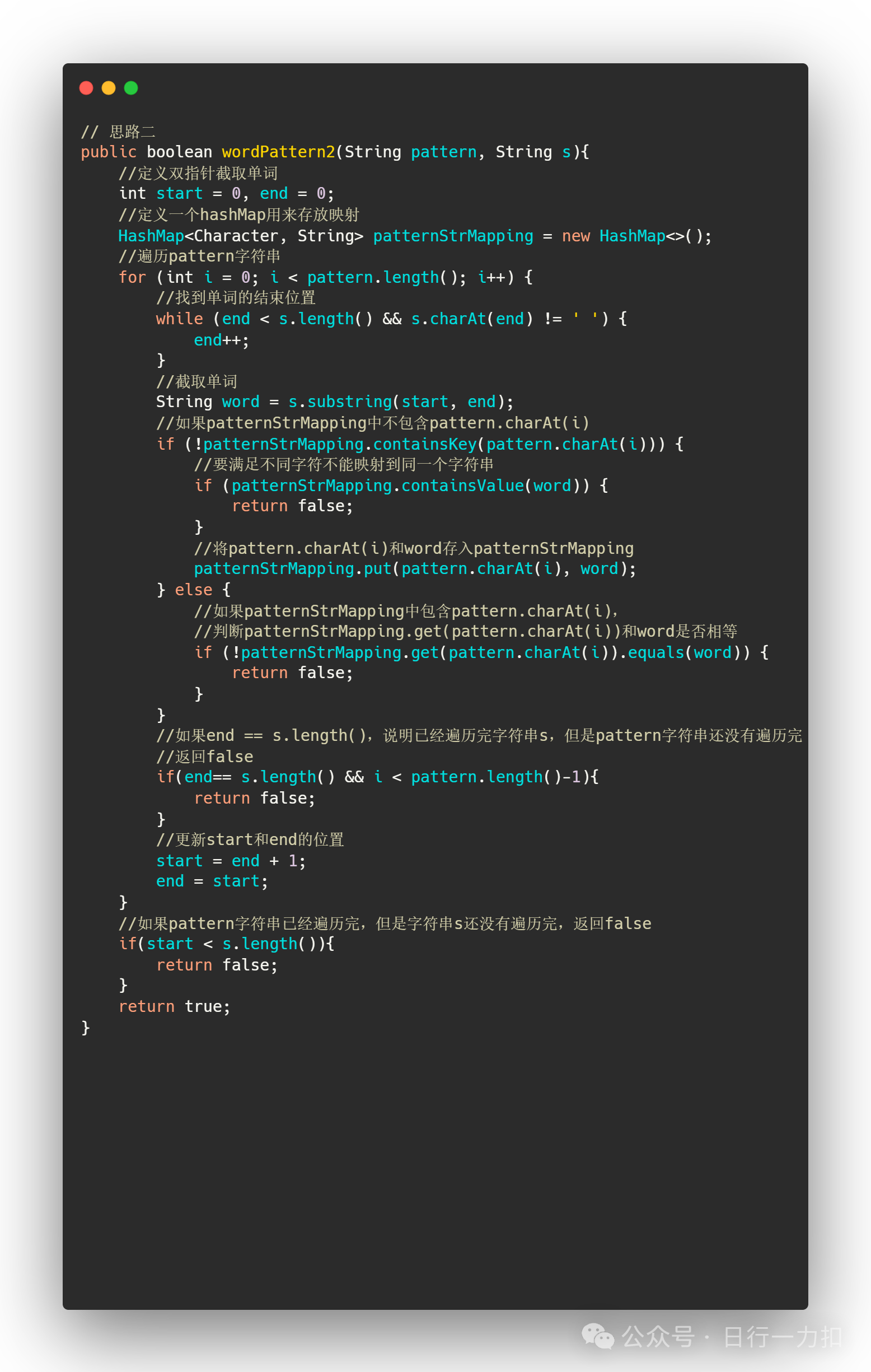
2.2 思路二——优化

由于在思路一将字符串s按空格分割成字符串数组String[] words = s.split(" ");浪费了一个和s接近一样大小的字符串数组，我们想一下怎么把这部分空间优化掉。

我们之所有将s字符串分割，就是因为我们向方便后续根据pattern的第几个字符就可以找到words中对应的第几个单词。

如果不使用额外的数组空间，我们就得想办法找到pattern字符对应的位置的单词。但是注意我要找的单词不是乱序的，是从前往后找的，pattern从第一个字符走到最后一个字符，对应s中的单词也是从第一个单词走到最后一个单词（先不考虑s中单词数量和pattern中字符数不相等的情况，因为如果不相等的话把短的那个遍历结束发现另外一个没遍历完就可以直接返回false）。

而且题目也告诉我们：

• s 中每个单词都被 单个空格 分隔

• s 不包含 任何前导或尾随对空格

所以如果要截取对应的单词，只需要指定两个指针，来截取对应位置的单词就可以了。

所以整体思路同思路一，只不过在使用words[i]时我们使用一个双指针，用来截取单词，减少额外的空间开销。（代码有注释）

但是我们需要注意：

• 我们需要考虑某一个先遍历完的情况，因为任何一个先遍历完（我指的是映射），就需要返回false，比如下图：

• 

3. 代码实现

3.1 思路一——hash映射表

3.2 思路二——优化空间

4. 相关复杂度分析

思路一：使用split方法

• 时间复杂度：

  • 分割字符串s：O(M)，其中M是字符串s的长度。

  • 遍历pattern字符串：O(N)，其中N是pattern的长度（同时也是分割后的单词数组的长度）。

  • 每次迭代中检查映射关系：O(1)平均时间复杂度，但包含对containsValue的调用，这在最坏情况下的时间复杂度为O(k)，k是映射中的元素数量。

  • 综合时间复杂度：O(M + Nk)，这里假设k在最坏情况下与N相等。

• 空间复杂度：

  • 存储单词数组：O(M)，因为需要存储分割后的单词。

  • 使用HashMap存储映射：O(N)，在最坏情况下，每个字符映射一个唯一的单词。

  • 综合空间复杂度：O(M + N)。

思路二：使用双指针法

• 时间复杂度：

  • 直接在s上使用双指针寻找单词，避免了split的使用：O(M)，其中M是字符串s的长度。

  • 遍历pattern：O(N)，其中N是pattern的长度。

  • 检查映射关系的时间复杂度与思路一相同，因此综合时间复杂度为：O(M + Nk)。

• 空间复杂度：

  • 不需要存储单词数组，直接在s上操作：O(1)额外空间（不计入输出结果的空间）。

  • 使用HashMap存储映射：O(N)，在最坏情况下，每个字符映射一个唯一的单词。

  • 综合空间复杂度：O(N)。

总结

第一种方法在空间复杂度上会稍高一些，因为它需要存储分割后的单词数组。

第二种方法在处理大文本时可能更优，因为它直接在原字符串上操作，避免了额外的存储开销。