量子计算:数据安全难题

当今数字技术面临的最大挑战之一是安全系统和数据。为此,人们设计了复杂的算法来加密数据并通过称为对称加密的框架来保护数据。虽然这已被证明是成功的,但量子计算的进步(利用量子力学比传统计算机更快地解决复杂问题)可能会彻底改变数据安全性。
IBM、微软和谷歌已经将注意力转向量子计算,因此商业上可行的量子计算机距离成为现实并不遥远。事实上,2023 年全球量子计算市场规模预计为 8.66 亿美元,预计到 2028 年将达到 43.75 亿美元,2023 年至 2028 年复合年增长率为 38.3%。这引发了人们的担忧:计算机可能会对当前的公钥加密算法构成威胁,并可能暴露敏感数据。因此,数据安全需要领先一步,采用更先进的加密算法来最大限度地减少潜在风险并确保量子计算世界中数据的安全。
我们的数据安全存在漏洞
对抗量子数据安全是一个令人担忧的问题,因为当前的数据保护方法使用传统计算能力需要数年时间才能破解的算法。然而,量子计算处理能力的提高将大大减少这个时间,其解决数学问题和加速某些复杂数学计算的能力可能会导致我们使用的加密算法变得过时。这将带来对企业、大学、政府等不利的风险。
Forrester 的一项研究支持了这一点,该研究预计量子计算机将能够在未来 5 到 30 年内破解所有当前的密码系统,大多数人声称在未来 5 年内发生这种情况的可能性高达 70%。因此,毫不奇怪,Gartner 强调为量子影响做好准备的重要性,鼓励在量子时代的预期中推广隐私增强技术。这是一个有效的建议,因为一些经典的密码算法将无法对抗量子计算的处理能力,并且会屈服于暴力攻击。
然而,虽然量子计算被广泛认为是数据安全的潜在风险,但它也可能成为解决方案的一部分,因为量子网络安全可能为保护关键数据提供更强大和更引人注目的机会。
量子网络安全
IBM表示,量子计算可以帮助提供比当前产品更强大的方式来保护关键数据。特别是,量子机器学习和量子随机数生成被认为可以提供一种可行的解决方案来保护数据,同时能够在量子时代的网络攻击造成损害之前检测并阻止它们。
由于加密通常是数据安全的关键组成部分,因此采用抗量子密码技术对于保护人员和遵守隐私法规至关重要。然而,由于量子计算尚未得到广泛应用,几年内我们不太可能利用量子计算能力来开发量子证明的数据安全方法。因此,在量子计算被广泛采用(最有可能成为量子计算即服务)之前,至关重要的是要领先于潜在威胁并立即开发量子证明解决方案,而不是等待量子计算机出现打破当前的数据加密模型。
数据安全的量子证明方法
为了为量子革命做好准备,公司需要评估其网络安全基础设施并识别量子计算的潜在漏洞。随着量子计算的大规模推广,一些传统形式的数据安全将被淘汰,但人们相信其他形式有能力抵御这种不断发展的技术的潜在威胁。
令牌化使用随机化来替换隐藏该值的令牌的实际值,被认为是针对量子计算的可行数据安全选项。这种随机化是一种强大的数据安全工具,与使用数学公式或证明来确保算法完整性的基于密钥的加密不同,它使用随机但可逆的令牌存储数据,这些令牌无法通过数学解决方案解密。
此外,代币化在整个企业中一致地用代币替代实际价值,这意味着数据可以在受保护的状态下加入,以支持人工智能、机器学习、数据分析计划和其他需要来自多个孤岛的数据来推动业务成果的应用程序。
为量子未来做好准备
量子计算的出现是一把双刃剑。虽然它有望为数据安全带来突破性的可能性,但它带来的风险同样令人担忧。因此,今天就需要为它的到来做好准备,以保证未来数据的安全。这得到了 IBM 的支持,该公司表示,虽然量子计算机尚未商用,但现在启动量子证明网络安全解决方案具有显着的优势。
尤其如此,因为恐怖分子网络可以使用与企业相同的技术。虽然企业可能会使用这些工具来改善客户体验并降低成本,但恶意行为者会利用它们来访问数据以用于其他目的。人们已经相信,威胁行为者正在抓取数据,这意味着他们正在窃取并保留数据,直到量子计算机更容易解密数据为止。为了克服这一挑战,公司现在需要实施量子证明解决方案,以确保数据在未来保持安全。
今天保护数据
尽管量子计算将产生的影响尚不清楚,但我们确实知道,我们不能等到它投入商业使用才实施更严格的安全措施来抵御其计算能力的威胁。因此,当今对数据安全的投资对于保护数据免受新兴威胁(例如量子计算带来的威胁)至关重要。
为了减轻未来的隐私威胁,公司需要重新思考如何确保数据安全。虽然量子计算和数据科学家正在努力开发可能具有量子防护能力的解决方案,但企业将从今天实施的解决方案中受益,这些解决方案被认为可以抵御威胁行为者和量子计算,这是实施多层方法的第一步。面向未来的数据安全。
只有当公司优先考虑数据保护并且不仅仅关注外围时,才能实现这一点。实现这一目标的最佳方式是与专业公司合作,在识别和分类敏感数据以及通过能够抵御量子计算的解决方案保护数据方面拥有丰富的经验,以确保当前和未来的数据安全。
相关文章:

量子计算:数据安全难题
当今数字技术面临的最大挑战之一是安全系统和数据。为此,人们设计了复杂的算法来加密数据并通过称为对称加密的框架来保护数据。虽然这已被证明是成功的,但量子计算的进步(利用量子力学比传统计算机更快地解决复杂问题)可能会彻底…...

CCF-B类SGP‘24 4月10日截稿!速速行动!
会议之眼 快讯 第22届SGP(Eurographics Symposium on Geometry Processing)即欧洲图形学几何处理专题讨论会将于 2024 年 6月24 -日至26日在美国麻省理工学院举行!SGP是传播几何处理新研究想法和尖端成果的首要学术会议。作为该领域的重要学术盛事,SGP会…...

阿里云服务器安装MySQL、Apache、PHP
节日期间突然想要自己搭建一个个人网站,于是在阿里云申请了一个可以免费使用3个月的服务器,申请的云市场产品Wordpress平台( ALinux3 LNMP PHP7.4)。官方教程使用的CentOs系统,和我申请的ALinux3操作有一些差异&#x…...
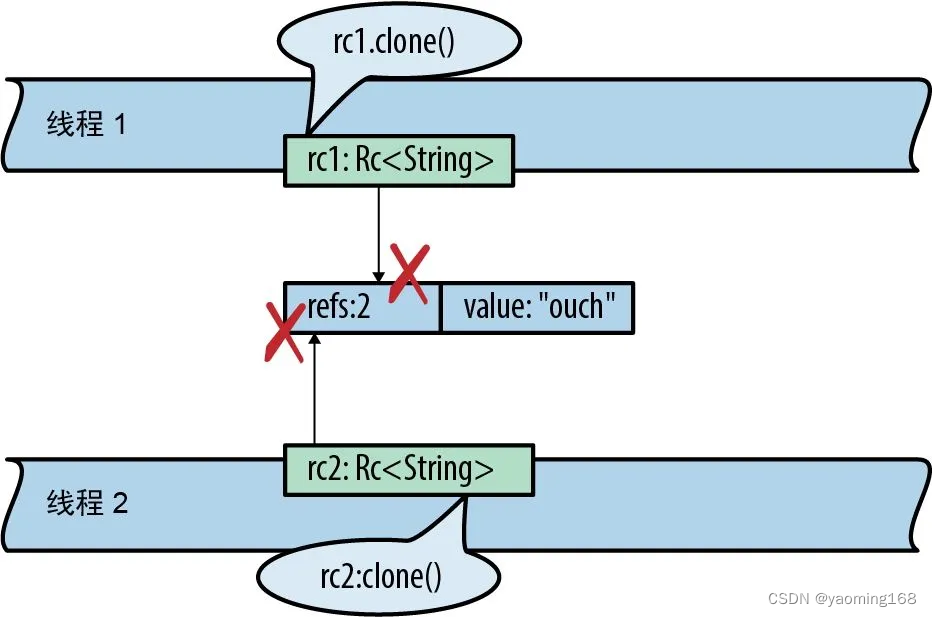
Rust基础拾遗--并发和异步编程
Rust基础拾遗 前言1.并发1.1 分叉与合并并行1.1.1 启动与联结1.1.2 跨线程错误处理1.1.3 跨线程共享不可变数据1.1.4 rayon 1.2 通道1.2.1 发送值1.2.2 接收值1.2.3 运行管道1.2.4 通道的特性与性能1.2.5 线程安全:Send与Sync 1.3 共享可变状态 2.异步编…...
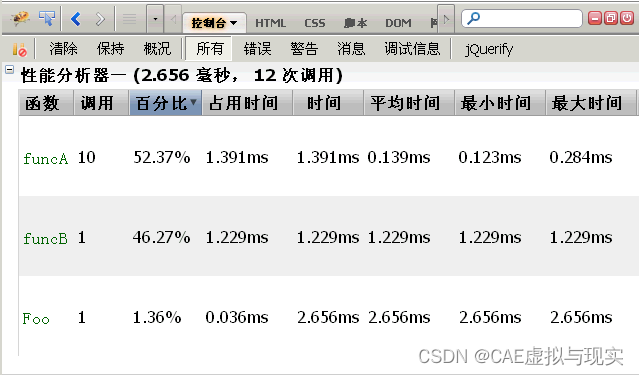
Javascript怎么输出内容?两种常见方式以及控制台介绍
javascript是一种非常重要的编程语言,在许多网页中它被广泛使用,可以实现许多交互效果和动态效果。输出是javascript中最基本的操作之一,下面将介绍两种常见的输出方式。 一、使用console.log()函数输出 console.log()函数是常用的输出函数…...

机器人路径平滑——线性插值
C++代码 //要实现平滑二维曲线的算法,你可以使用贝塞尔曲线或B样条曲线。下面是一个使用B样条曲线的C++算法的示例:#include <iostream> #include <vector> #include <fstream> #include <iomanip>...
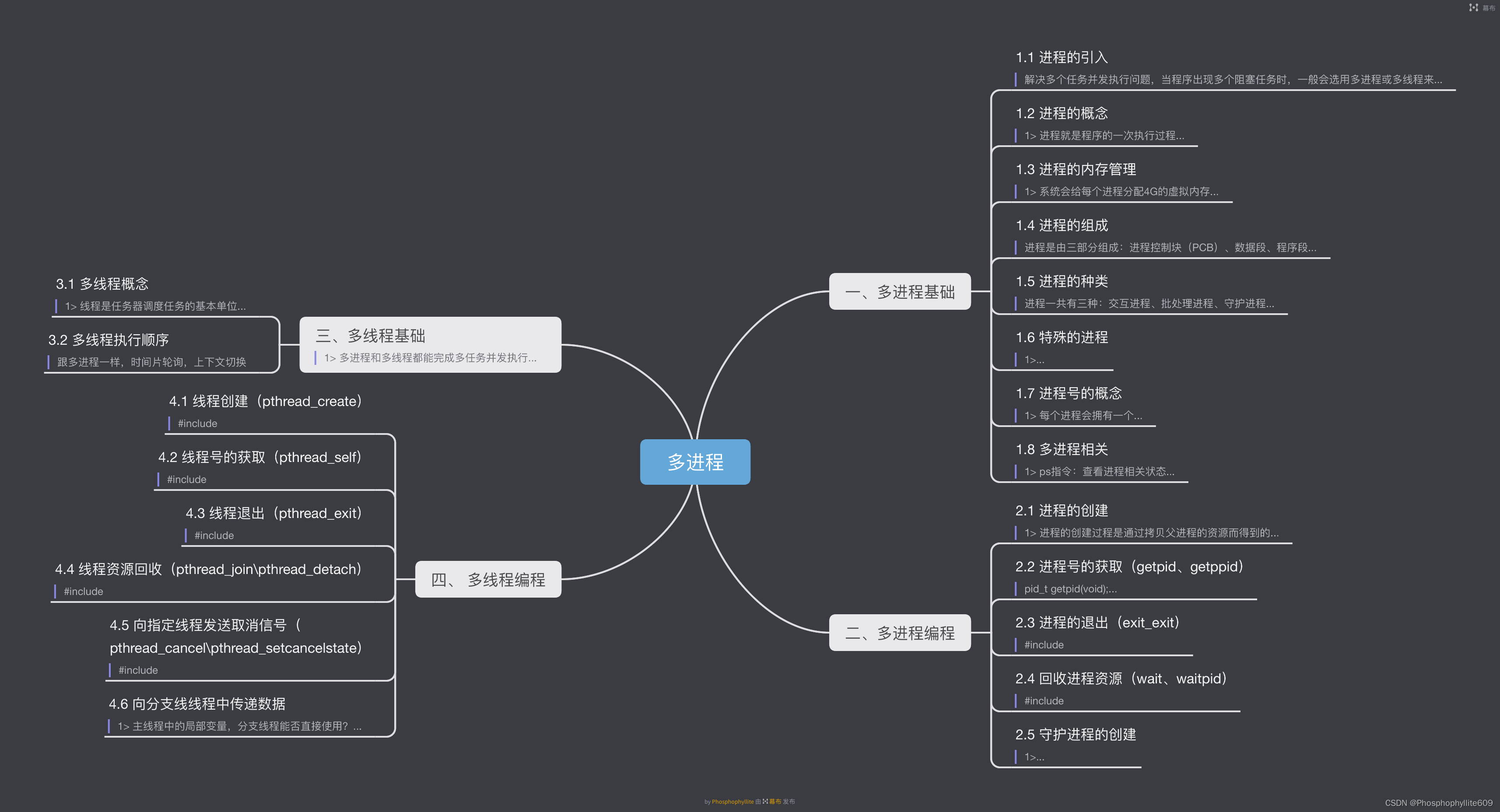
2024-2-21-多线程基础作业
作业: 源代码: #include <myhead.h> #define MAXSIZE 64 //定义要传递的结构体类型 struct Info {const char *src;const char *dest;int len; }; int get_file_len(const char *srcfile, const char *destfile) {//以只读的形式打开源文件int sr…...

MySQL8的ONLY_FULL_GROUP_BY SQL模式兼容问题
文章目录 1. 问题描述2. 解决方法1. 修改查询2. 修改SQL模式3. 使用ANY_VALUE()函数 1. 问题描述 Cause: java.sql.SQLSyntaxErrorException: Expression #1 of SELECT list is not in GROUP BY clause and contains nonaggregated column btc-cloud.t1.id which is not funct…...
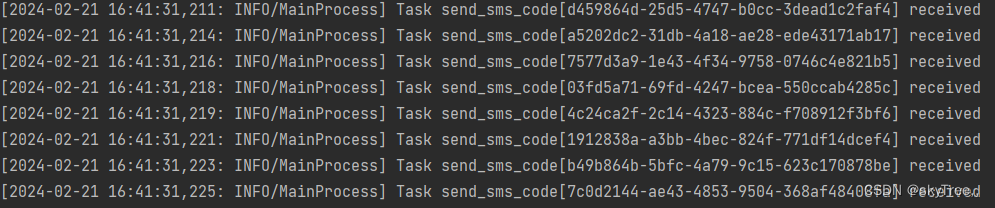
Django使用Celery异步
安装包 pip install celerypip install eventlet 1.在项目文件的根目录下创建目录结果 2. 在main.py文件中 # !/usr/bin/env python # -*-coding:utf-8 -*-""" # Author :skyTree # version :python 3.11 # Description&#…...
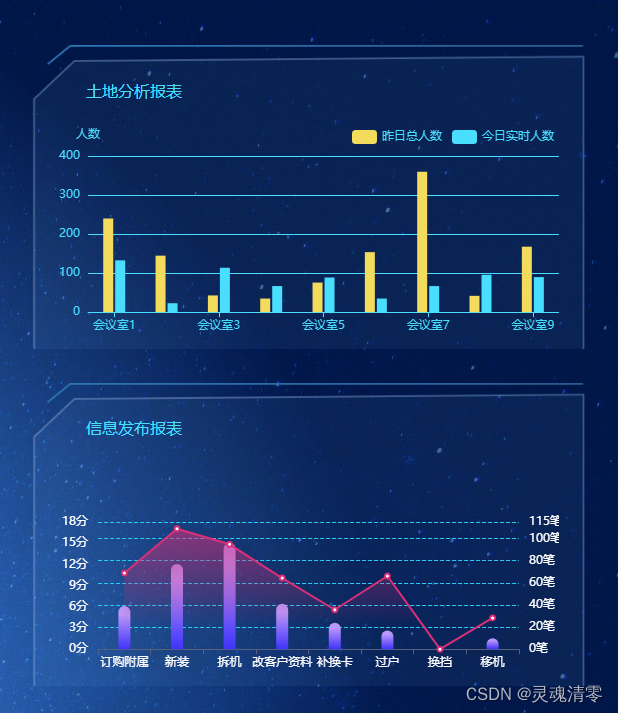
vue3 + ts + echart 实现柱形图表
首先封装Echart一个文件 代码如下 <script setup lang"ts"> import { ECharts, EChartsOption, init } from echarts; import { ref, watch, onMounted, onBeforeUnmount } from vue;// 定义props interface Props {width?: string;height?: string;optio…...
c语言结构体与共用体
前面我们介绍了基本的数据类型 在c语言中 有一种特殊的数据类型 由程序员来定义类型 目录 一结构体 1.1概述 1.2定义结构体 1.3 结构体变量的初始化 1.4 访问结构体的成员 1.5结构体作为函数的参数 1.6指向结构的指针 1.7结构体大小的计算 二共用体 2.1概述 2.2 访…...

vue系列--vue封装拖拽指令v-drag
1.首先将下面的代码引入代码中 export const initVDrag (Vue) > {Vue.directive("drag", (el) > {const oDiv el // 当前元素const minTop oDiv.getAttribute("drag-min-top")const ifMoveSizeArea 20oDiv.onmousedown (e) > {let target …...

devc++ 使用 winsock 实现 UDP 局域网 WIFI 广播
参考链接 使用UDP发送广播报_udp广播 inaddr_broadcast-CSDN博客 UDP接收端收不到广播的消息问题排查_unity upd广播连接不上是什么情况-CSDN博客 如何禁用自己电脑的虚拟网卡-百度经验 (baidu.com) 但是wifi 会屏蔽255.255.255.255 广播地址,所以 255.255.255.2…...
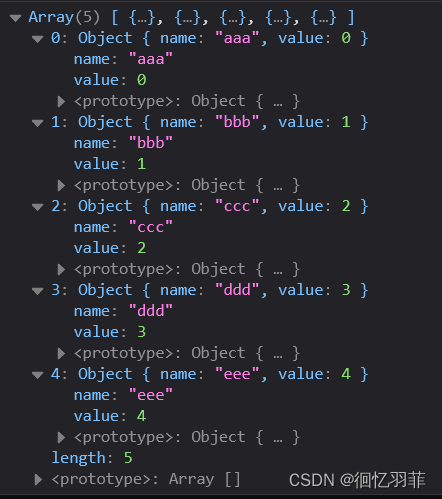
JS实现根据数组对象的某一属性排序
JS实现根据数组对象的某一属性排序 一、冒泡排序(先了解冒泡排序机制)二、根据数组对象的某一属性排序(引用sort方法排序) 一、冒泡排序(先了解冒泡排序机制) 以从小到大排序为例,冒泡排序的原…...

CSP-J 2023 复赛第2题:公路 ← 贪心算法
【题目来源】https://www.luogu.com.cn/problem/P9749https://www.acwing.com/problem/content/5311/【题目描述】 小苞准备开着车沿着公路自驾。 公路上一共有 n 个站点,编号为从 1 到 n。 其中站点 i 与站点 i1 的距离为 vi 公里。 公路上每个站点都可以加油&…...

【LeetCode打卡】Day23|669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
学习目标: 669. 修剪二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树 学习内容: 669. 修剪二叉搜索树 题目链接&&文章讲解 给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪…...
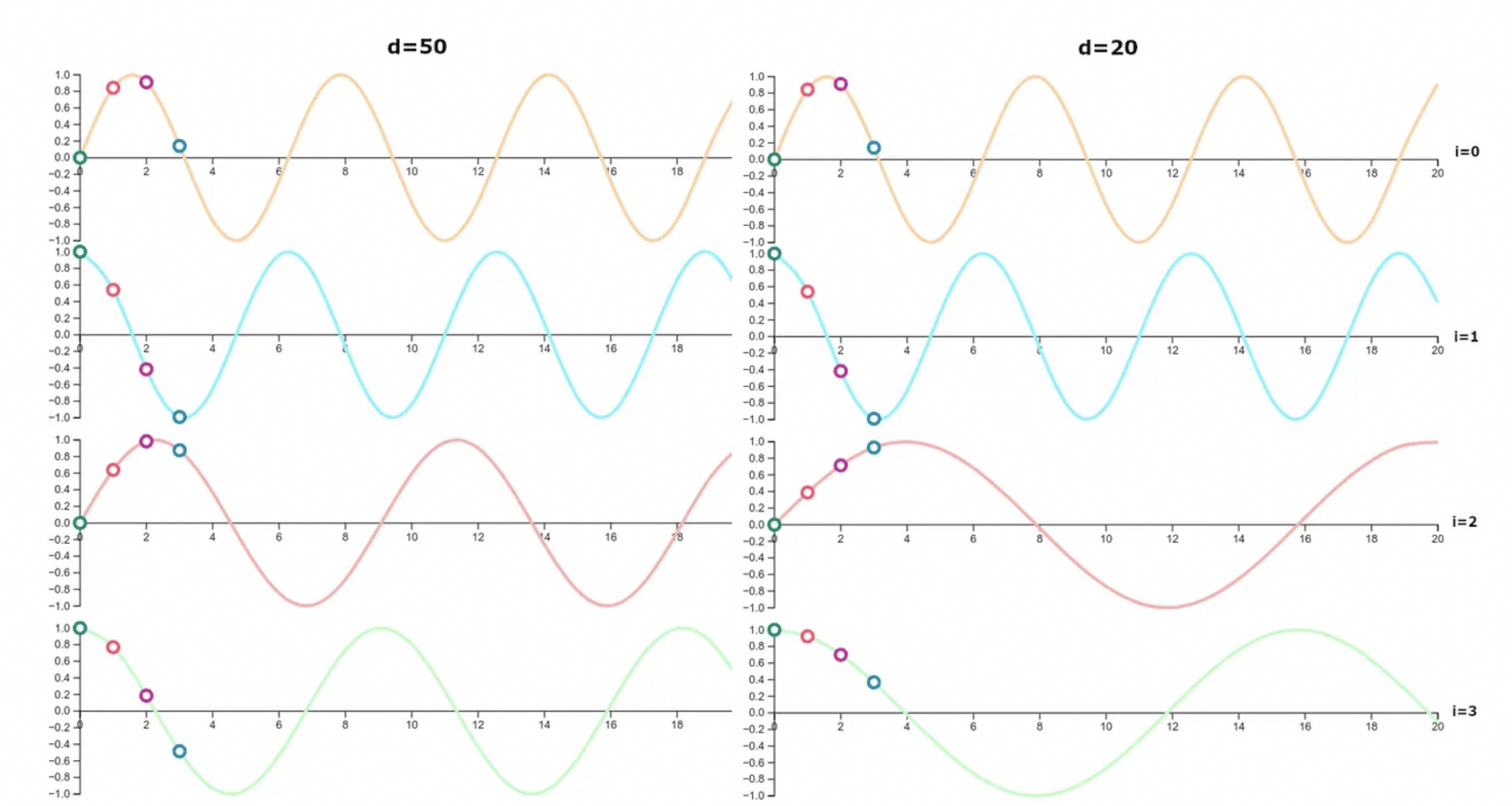
Transformer位置表示(Position Encoding)
为什么需要位置表示 对比CNN、RNN和Self-Attention: CNN处理相邻窗口的内容;RNN天然是序列操作,考虑了位置先后关系;Self-Attention的计算时是无序的,所以需要位置表示来知道Token之间的位置信息。 绝对位置表示 典型如…...

LPDDR6与LPDDR5 State Diagram技术探讨
相对于LPDDR5: 1)去掉DSM 2)idle到per-bank-refresh变成per-2-bank-refresh,LPDDR6下可自由组合任两个bank刷新,以提高性能 3)sref到进入command bus training后可MRR、MRW、CAS、MPC等命令 4)idle power down期间可MRR、MRW、CAS、MPC等命令 5)idle到进入command bus train…...
)
AliLinux的使用Docker初始化服务(详细)
AliLinux的使用Docker初始化服务(详细) AliLinux是基于CentOS的。 1、java 环境 2、mysql环境 3、kafka环境 4、flink环境 5、dinky环境 这些环境,本想直接dnf安装在宿主机上,思来想去,还是用docker方便学习&…...
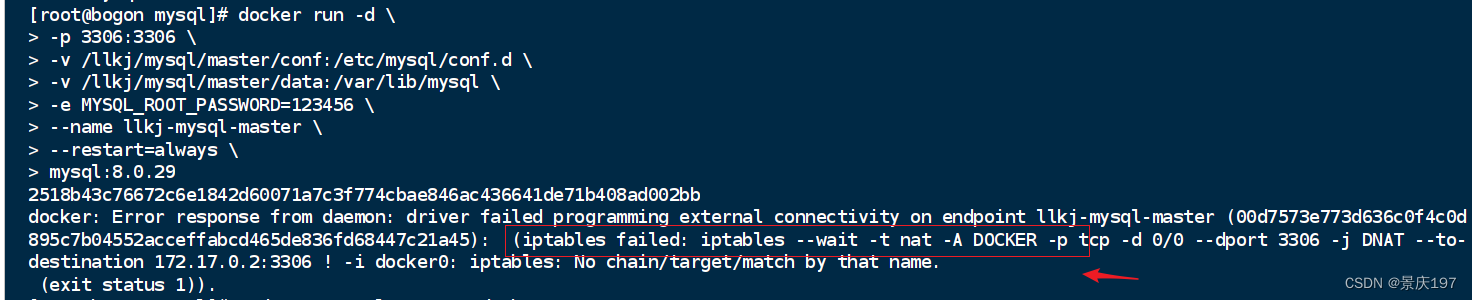
docker环境常用容器安装
目录 1.安装partainer 2.安装myql 3.安装redis 4.安装Minio 5.安装zibkin 6.安装nacos 7.安装RabbitMq 8.安装RocketMq 8.1启动service 8.2修改对应配置 8.3启动broker 8.4启动控制台 9.安装sentinel 10.安装elasticsearch 11.安装Kibana 12.安装logstash/file…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
