机器学习基本概念(李宏毅课程)
目录
- 一、概念:
- 1、机器学习概念:
- 2、深度学习概念:
- 二、深度学习中f(.)的输入和输出:
- 1、输入:
- 2、输出:
- 三、三种机器学习任务:
- 1、Regression回归任务介绍:
- 2、Classification分类任务介绍:
- 3、Structured Learning创造性学习:
- 四、机器学习步骤(模型训练阶段):
- 第一步:定义一个含有未知参数的函数(以线性函数为例):
- 第二步: 定义损失函数:
- 第三步: 寻找最优的w、b使得Loss最小:
- 1.梯度下降:
- 五、线性函数和复杂函数:
- 1、线性函数定义:
- 2、非线性函数定义:
- 3、如何表示出Hard Sigmoid函数:
- 4、对(四)中案例的深入理解(以非线性函数为例):
- 5.多特征预测单变量+非线性函数:
一、概念:
1、机器学习概念:
机器学习 ≈ 训练生成一个函数f(.) ,这个函数相当复杂。
例如:

2、深度学习概念:
机器学习的目的是寻找一个满足需求的函数f(.),但是具体使用什么方式寻找f(.)没有说明。
深度学习为机器学习领域的一个子领域,故深度学习给出了寻找函数的方法,即通过“神经网络”来训练生成一个函数f(.) 。
例如:
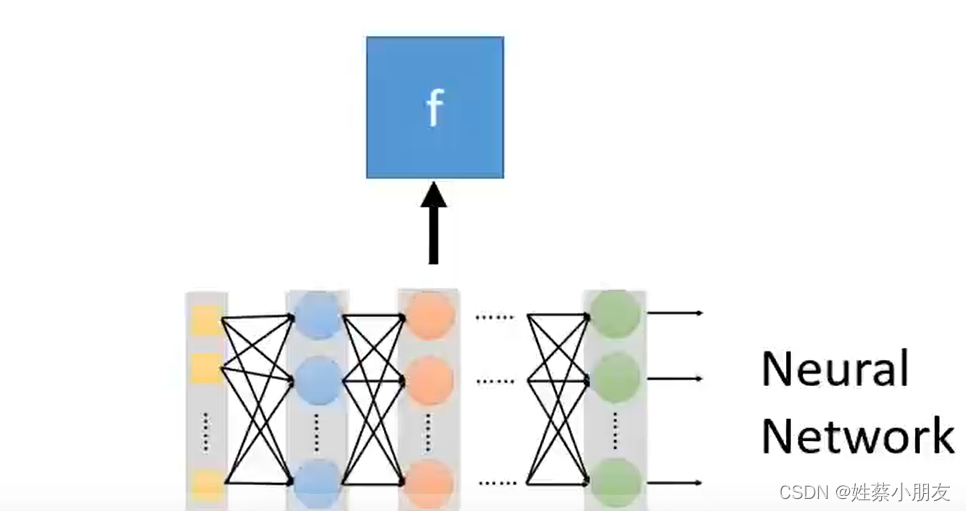
二、深度学习中f(.)的输入和输出:
1、输入:
函数f(.)的输入可以是向量、矩阵、序列,根据不同场景使用不同的输入。
- 向量
- 矩阵:图像识别领域,一张图片可以转换成矩阵表示
- 序列:序列预测、语音辨识、文字翻译领域输入可以转换成序列表示

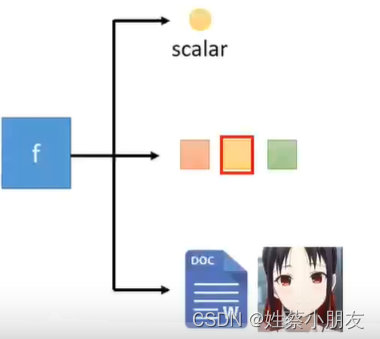
2、输出:
根据不同任务需求f(.)的输出不同。
- 数值
- 类别:分类任务
- 句子、图片:翻译任务、图片生成
三、三种机器学习任务:
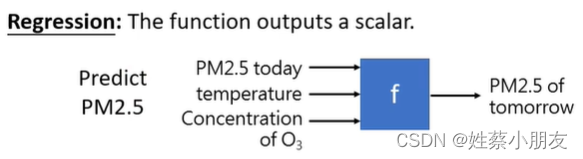
1、Regression回归任务介绍:
函数输入:过往PM2.5数据以及影响PM2.5的特征值
函数输出:预测未来PM2.5的值
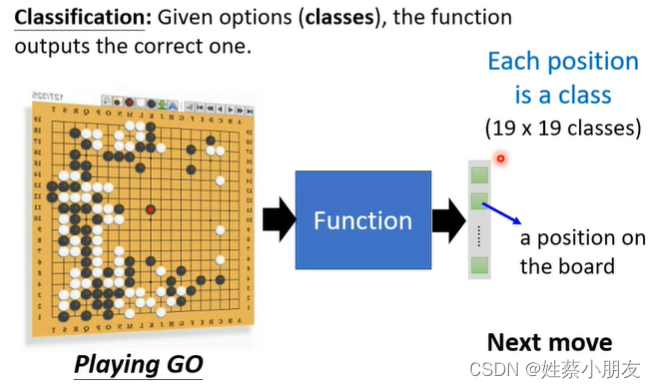
2、Classification分类任务介绍:
函数输入:棋盘中黑子白子位置
函数输出:从19*19个选项中选择下一个落子位置
3、Structured Learning创造性学习:
函数输出:图片、文档等有结构的文件
四、机器学习步骤(模型训练阶段):
这里以回归任务为例:目标是根据2/25日浏览量数据预测2/26日浏览量数据。
第一步:定义一个含有未知参数的函数(以线性函数为例):

以最简单的线性回归函数y=b+Wx为例(当然机器学习的函数基本上不会这么简单):
- 函数y=b+Wx即为平时称呼的模型
- x为函数输入,输入的是2/25日浏览量数据
- y为函数输出,输出的是未来2/26日浏览量数据
- w和b都是超参数,初始为位置数,在模型训练过程中不断更新参数使得函数的输出值不断精确(模型训练阶段的最终目的是:训练集训练+验证集预测过程不断更新w和b),力图训练一个预测效果最优的模型
- 其中w为x的权重,b为偏置值
第二步: 定义损失函数:

损失函数L(b,w)是一个已写好的函数,用于模型训练阶段每次更新超参数w和b时都会在验证集上使用该组w和b计算预测值,然后比较预测值和真实值的差异(损失),从而衡量本组训练得到的超参数w和b是否能使得模型预测效果最优。
- 损失函数的输入为超参数b和w
- Loss越大,即表示当前的一组b和w越差,Loss越小,即表示当前的一组b和w越优秀。
第三步: 寻找最优的w、b使得Loss最小:
1.梯度下降:
使用梯度下降法不断更新w和b,使得每次获得一组新的w和b(wn和bn)。
不断执行第二步和第三步使得获得最优的w和b(w和b)。
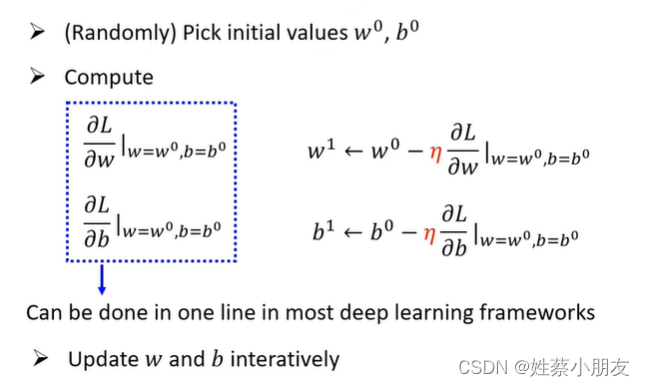
- 其中η为学习率,用来控制梯度下降的快慢程度,也是一个超参数。
五、线性函数和复杂函数:
1、线性函数定义:
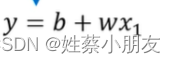
同(五),以最简单的线性回归函数y=b+Wx为例(当然机器学习的函数基本上不会这么简单):
- x为函数输入,输入的是2/25日浏览量数据
- y为函数输出,输出的是未来2/26日浏览量数据
- w和b都是超参数,初始为位置数,在模型训练过程中不断更新参数使得函数的输出值不断精确(模型训练阶段的最终目的是:训练集训练+验证集预测过程不断更新w和b),力图训练一个预测效果最优的模型
- 其中w为x的权重,b为偏置值
2、非线性函数定义:
线性函数y=wx+b不管超参数w和b如何变化,函数始终是一条直线,所以线性函数在处理具有复杂关系的xy时不适用。
- 对于复杂函数,我们可以用简单的蓝色函数(Hard Sigmoid函数)叠加的方式来获得一个复杂函数,如下图所示:
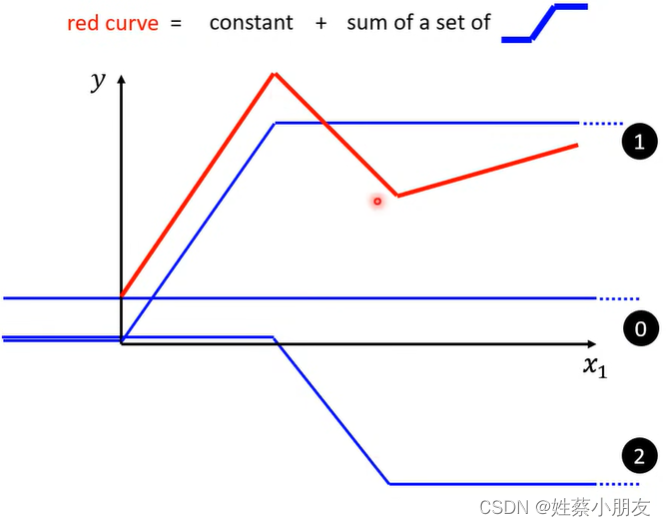
- 对于曲线函数,我们可以对曲线每段取微分,每个微元看做是一个蓝色函数(Hard Sigmoid函数),无数个蓝色函数叠加也可以获得任意的曲线函数。
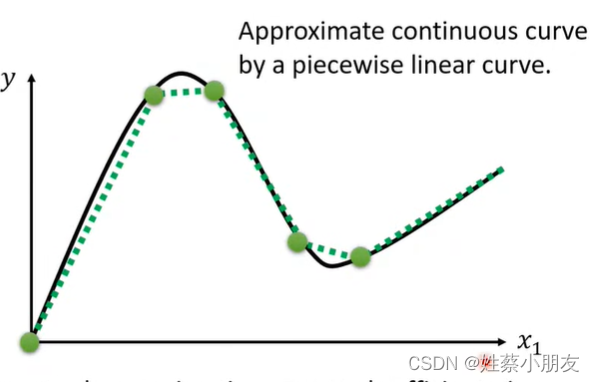
3、如何表示出Hard Sigmoid函数:
各种曲线都可以通过蓝色函数(Hard Sigmoid)的叠加来表示,那么Hard Sigmoid函数又要如何表示?
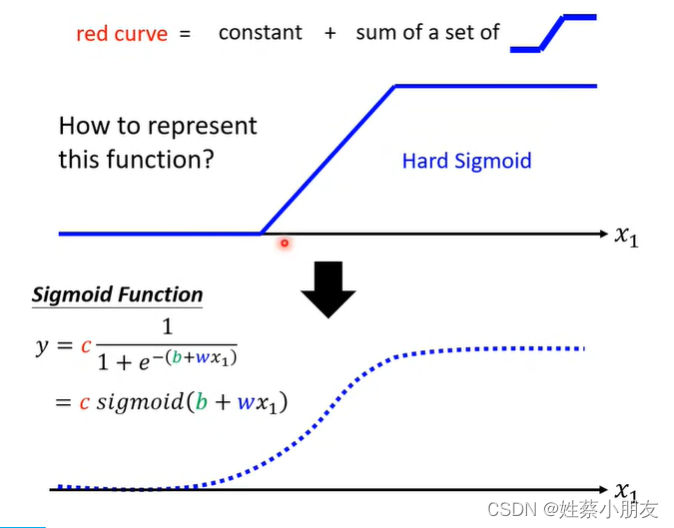
有一种函数叫做sigmoid函数,该函数可以逼近任何的hard sigmoid函数,所以一般使用sigmoid函数来表示hard sigmoid函数。
从sigmoid函数的公式可以看出:
- 通过改变w可以改变函数的斜率
- 通过改变v可以改变函数的位置
- 通过改变c可以改变函数的高度
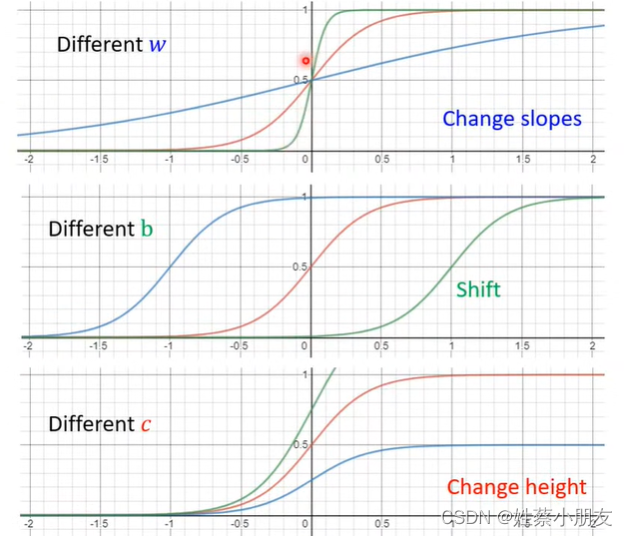
因此,通过不同的sigmoid函数叠加我们可以获得任意的函数曲线。
4、对(四)中案例的深入理解(以非线性函数为例):
(四)中我们以线性函数y=wx+b为例,假设x和y是线性关系。其中x输入为2/25日浏览量数据,y输出为2/26日浏览量数据。而在现实中x和y不可能是简单的线性关系,那么函数应该如何表示?当然是使用我们的sigmoid函数:
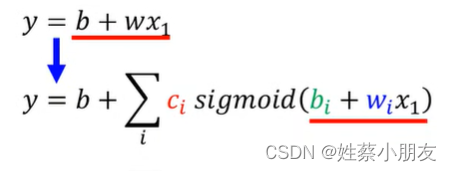
进一步设想,案例中我们用2/25日浏览量数据预测2/26日浏览量数据,属于单特征,此时仅有一个输入x和一个输出y,如果我们输入数据为多特征,即要用2/01~2/25这25天的浏览量预测2/26日浏览量数据,函数应如何表示?很简单,数据中有25个特征,每个特征xi与y之间都有一个权重值wi, 因此多特征预测单变量的线性函数关系和非线性函数关系表示如下:
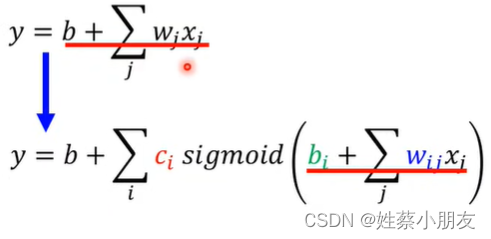
5.多特征预测单变量+非线性函数:
下面我们举个例子来深度理解多特征预测单变量+非线性函数
相关文章:

机器学习基本概念(李宏毅课程)
目录 一、概念:1、机器学习概念:2、深度学习概念: 二、深度学习中f(.)的输入和输出:1、输入:2、输出: 三、三种机器学习任务:1、Regression回归任务介绍:2、Classification分类任务介绍:3、Stru…...
浅谈WPF之利用RichTextBox实现富文本编辑器
在实际应用中,富文本随处可见,如留言板,聊天软件,文档编辑,特定格式内容等,在WPF开发中,如何实现富文本编辑呢?本文以一个简单的小例子,简述如何通过RichTextBox实现富文…...

w29pikachu-ssrf实例
SSRF简介 SSRF是服务器端请求伪造 危害: 1.可以对服务器所在内网、本地进行端口扫描,获取一些服务的信息等 2.目标网站本地敏感数据的读取 3.内外网主机应用程序漏洞的利用 4.内外网web站点漏洞的利用 ssrf常用的相关协议: gopher://: 发…...

使用 openssl 进行哈希计算
版本:OpenSSL 3.0.2 15 Mar 2022 (Library: OpenSSL 3.0.2 15 Mar 2022) SHAx 系列 如果对象完全存储在内存中,可以使用以下函数: #include <openssl/sha.h>unsigned char *SHA1(const unsigned char *data, size_t count, unsigned…...
深度学习基础——SSD目标检测
SSD网络介绍 使用多个特征图作为特征预测层。 SSD (Single Shot MultiBox Detector)于2016年提出。当网络输入为300300大小时,在VOC2007测试集上达到74.3%的mAP;当输入是512512大小时,达到了76.9%的mAP SSD_Backbone部分介绍 不变的部分 特征提取网…...
鸿蒙系统优缺点,能否作为开发者选择
凡是都有对立面,就直接说说鸿蒙的优缺点吧。 鸿蒙的缺点: 鸿蒙是从2019年开始做出来的,那时候是套壳Android大家都知晓。从而导致大家不看鸿蒙系统,套壳Android就是多次一举。现在鸿蒙星河版已经是纯血鸿蒙,但是它的…...
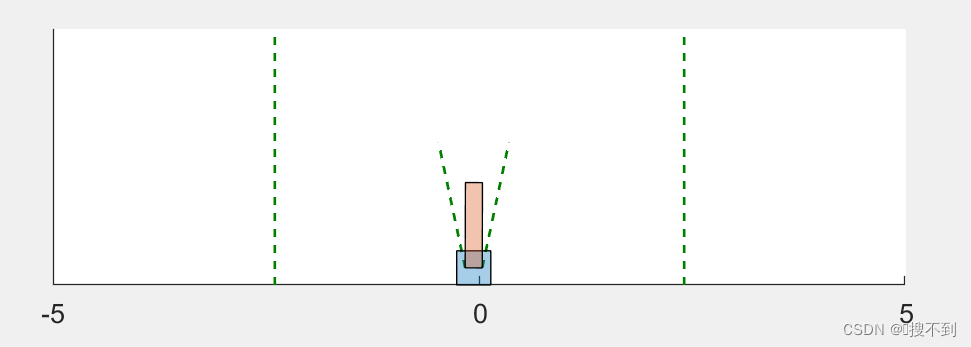
强化学习入门(Matlab2021b)-创建环境【2】
目录 1 前言2 利用step和reset函数创建自定义环境2.1 对象描述2.2 reset函数2.3 step函数2.3 构建自定义环境3 使用匿名函数传递额外的参数4 可视化检查自定义函数的输出参考链接1 前言 本文介绍如何基于MATLAB编写step、reset函数,创建自己的强化学习环境(Environment)。 使…...

OkHttp 相关问题
1、OkHttp请求整体流程是怎么样? Request-》OkHttpClient-》RealCall 同步 -》 在调用线程 执行五大拦截器 异步 -》 使用分发器将任务在线程池执行 五大拦截器 ---首先AsyncCall --加到等待队列readyAsyncCalls--》判断host有没有 已经存在。有,就赋值原来的。(reuseC…...

html的表单标签(上):form标签和input标签
表单标签 表单是让用户输入信息的重要途径。 用表单标签来完成与服务器的一次交互,比如你登录QQ账号时的场景。 表单分成两个部分: 表单域:包含表单元素的区域,用form标签来表示。表单控件:输入框,提交按…...
)
网页数据的解析提取(XPath的使用----lxml库详解)
在提取网页信息时,最基础的方法是使用正则表达式,但过程比较烦琐且容易出错。对于网页节点来说,可以定义id、class或其他属性,而且节点之间还有层次关系,在网页中可以通过XPath或CSS选择器来定位一个或多个节点。那么&…...

dell r740服务器黄灯闪烁维修现场解决
1:首先看一下这款DELL非常主力的PowerEdge R740服务器长啥样,不得不说就外观来说自从IBM抛弃System X系列服务器后,也就戴尔这个外观看的比较顺眼。 图一:是DELL R740前视图(这款是8盘机型) 图二ÿ…...

202426读书笔记|《尼采诗精选》——高蹈于生活之上,提升自己向下观望
202426读书笔记|《尼采诗精选》——高蹈于生活之上,提升自己向下观望 第一辑 早期尼采诗歌选辑(1858—1869年)第二辑 前期尼采遗著中的诗歌选辑(1871—1882年)第五辑 戏谑、狡计与复仇——德语韵律短诗序曲(…...
【PX4学习笔记】13.飞行安全与炸机处理
目录 文章目录 目录使用QGC地面站的安全设置、安全绳安全参数在具体参数中的体现安全绳 无人机炸机处理A:无人机异常时控操作B:无人机炸机现场处理C:无人机炸机后期维护和数据处理D:无人机再次正常飞行测试 无人机飞行法律宣传 使…...
Puppeteer 使用实战:如何将自己的 CSDN 专栏文章导出并用于 Hexo 博客(二)
文章目录 上一篇效果演示Puppeteer 修改浏览器的默认下载位置控制并发数错误重试并发控制 错误重试源码 上一篇 Puppeteer 使用实战:如何将自己的 CSDN 专栏文章导出并用于 Hexo 博客(一) 效果演示 上一篇实现了一些基本功能,…...

[ 2024春节 Flink打卡 ] -- 优化(draft)
2024,游子未归乡。工作需要,flink coding。觉知此事要躬行,未休,特记 资源配置调优内存设置 TaskManager内存模型 https://nightlies.apache.org/flink/flink-docs-release-1.18/docs/deployment/config/ TaskManager 内存模型…...

电脑进水无法开机怎么办 电脑进水开不了机的解决方法
意外总是会不定时打破你的计划,电脑这类电器最怕遇到的除了火还有水,设备进水会导致数据丢失,那么我们遇到电脑进水怎么办?进水之后不正确处理也会引起很多不必要的麻烦. 解决办法 第一步:关机 如果您的电脑是在开…...

【Flutter】底部导航BottomNavigationBar的使用
常用基本属性 属性名含义是否必须items底部导航栏的子项List是currentIndex当前显示索引否onTap底部导航栏的点击事件, Function(int)否type底部导航栏类型,定义 [BottomNavigationBar] 的布局和行为否selectedItemColor选中项图标和label的颜色否unsel…...
Vue封装全局公共方法
有的时候,我们需要在多个组件里调用一个公共方法,这样我们就能将这个方法封装成全局的公共方法。 我们先在src下的assets里新建一个js文件夹,然后建一个common.js的文件,如下图所示: 然后在common.js里写我们的公共方法,比如这里我们写了一个testLink的方法,然后在main…...

雪花算法生成分布式主键ID
直接上代码,复制即可使用 public class SnowflakeIdGenerator {private static final long START_TIMESTAMP 1624000000000L; // 设置起始时间戳,2021-06-18 00:00:00private static final long DATA_CENTER_ID_BITS 5L;private static final long WO…...

第三百五十九回
文章目录 1. 概念介绍2. 使用方法3. 代码与效果3.1 示例代码3.2 运行效果 4. 内容总结 013pickers2.gif 我们在上一章回中介绍了"如何实现Numberpicker"相关的内容,本章回中将介绍wheelChoose组件.闲话休提,让我们一起Talk Flutter吧。 1. 概念…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
