常见的排序算法整理
1.冒泡排序
1.1 冒泡排序普通版
每次冒泡过程都是从数列的第一个元素开始,然后依次和剩余的元素进行比较,若小于相邻元素,则交换两者位置,同时将较大元素作为下一个比较的基准元素,继续将该元素与其相邻的元素进行比较,直到数列的最后一个元素 .(最后的元素最大,也是最先固定)
import java.util.Arrays;public class BubbleSort {public static void main(String[] args) {int[] arr = new int[]{9, 2, 1, 0, 5, 3, 6, 4, 8, 7};System.out.println("排序前:" + Arrays.toString(arr));sort(arr);System.out.println("排序后:" + Arrays.toString(arr));}// 冒泡排序方法public static void sort(int[] arr) {// 第一层for循环,用来控制冒泡的次数for (int i = 1; i < arr.length; i++) {// 第二层for循环,用来控制冒泡一层层到最后for (int j = 0; j < arr.length - 1; j++) {// 如果前一个数比后一个数大,两者调换,意味着泡泡向上走了一层if (arr[j] > arr[j + 1]) {int temp = arr[j]; // 临时变量temp用来交换两个数值arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}
}运行结果:
排序前:[9, 2, 1, 0, 5, 3, 6, 4, 8, 7]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
1.2 冒泡排序升级版
在这个版本中,改动了两点 . 第一点是加入了一个布尔值,判断第二层循环中的调换有没有执行,如果没有进行两两调换,说明后面都已经排好序了,已经不需要再循环了,直接跳出循环,排序结束 ; 第二点是第二层循环不再循环到arr.length - 1,因为外面的i循环递增一次,说明数组最后就多了一个排好序的大泡泡.第二层循环也就不需要到最末尾一位了,可以提前结束循环
/**
-
升级版冒泡排序:
-
加入一个布尔变量,如果内循环没有交换值,说明已经排序完成,提前终止
*/
import java.util.Arrays;public class BubbleSort {public static void main(String[] args) {int[] arr = new int[]{9, 2, 1, 0, 5, 3, 6, 4, 8, 7};System.out.println("排序前:" + Arrays.toString(arr));plusSort(arr);System.out.println("排序后:" + Arrays.toString(arr)); }// 升级版冒泡排序方法public static void plusSort(int[] arr) {if (arr != null && arr.length > 1) {for (int i = 0; i < arr.length - 1; i++) {// 初始化一个布尔值,用于标记此次循环内是否进行了交换操作boolean flag = true;for (int j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换arr[j]与arr[j+1]的值int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;// 改变flag的值,表示进行了交换操作flag = false;}}// 如果flag为true,表示在此次循环中没有进行交换操作,即已经完成了排序,提前终止外层循环if (flag) {break;}}}}
}运行结果:
排序前:[9, 2, 1, 0, 5, 3, 6, 4, 8, 7]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
2.选择排序
选择排序也是一种简单直观的排序算法,实现原理比较直观易懂:首先在未排序数列中找到最小元素,然后将其与数列的首部元素进行交换,然后,在剩余未排序元素中继续找出最小元素,将其与已排序数列的末尾位置元素交换。以此类推,直至所有元素都排序完毕
/**
-
选择排序:
-
每一次从待排序的数据元素中选出最小(或最大)的一个元素,
-
存放在序列的起始位置,直到全部待排序的数据元素排完。
*/
import java.util.Arrays;public class SelectSort {public static void main(String[] args) {int[] arr = new int[] {3, 4, 5, 7, 1, 2, 0, 9, 3, 6, 8}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组selectSort(arr); // 调用选择排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}// 选择排序方法public static void selectSort(int[] arr) {// 外层循环控制当前需要进行比较的元素索引位置for (int i = 0; i < arr.length - 1; i++) {int minIndex = i; // 设定当前循环的起始位置为最小值的位置// 内层循环寻找未排序部分中的最小值的索引for (int j = i + 1; j < arr.length; j++) {if (arr[minIndex] > arr[j]) {minIndex = j; // 如果当前位置的值比起始位置的值小,则更新最小值的索引}}// 如果找到最小值的索引与当前循环位置不同,则交换两个位置的值,将最小值交换至当前位置if (i != minIndex) {int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}}
}运行结果:
排序前:[3, 4, 5, 7, 1, 2, 0, 9, 3, 6, 8]
排序后:[0, 1, 2, 3, 3, 4, 5, 6, 7, 8, 9]
3.插入排序
一次插入排序的操作过程:将待插元素,依次与已排序好的子数列元素从后到前进行比较,如果当前元素值比待插元素值大,则将移位到与其相邻的后一个位置,否则直接将待插元素插入当前元素相邻的后一位置,因为说明已经找到插入点的最终位置(类似于打牌)
/**
-
插入排序:
-
从第一个元素开始,该元素可以认为已经被排序
-
取出下一个元素,在已经排序的元素序列中从后向前扫描
-
如果该元素(已排序)大于新元素,将该元素移到下一位置
-
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
-
将新元素插入到该位置后
-
重复上面步骤
*/
import java.util.Arrays;public class InsertSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组insertSort(arr); // 调用插入排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}// 插入排序方法public static void insertSort(int[] arr) {// 外层循环控制插入的元素索引位置for (int i = 1; i < arr.length; i++) {int temp = arr[i]; // 保存当前需要插入的元素值int j;// 内层循环比较并将元素插入到正确的位置for (j = i - 1; j >= 0 && temp < arr[j]; j--) {arr[j + 1] = arr[j]; // 将元素往后移动}arr[j + 1] = temp; // 将当前元素插入到正确位置}}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
4.快速排序
快速排序算法利用的是一趟快速排序,基本内容是选择一个数作为准基数,然后利用这个准基数将遗传数据分为两个部分,第一部分比这个准基数小,都放在准基数的左边,第二部分都比这个准基数大,放在准基数的右边.
import java.util.Arrays;
/**
-
快速排序:
-
快速排序算法利用的是一趟快速排序,基本内容是选择一个数作为准基数,
-
然后利用这个准基数将遗传数据分为两个部分,第一部分比这个准基数小,
-
都放在准基数的左边,第二部分都比这个准基数大,放在准基数的右边.
*/
public class QuickSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组quickSort(arr, 0, arr.length - 1); // 调用快速排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}/*** 快速排序方法* @param arr 待排序的数组* @param begin 排序起始位置* @param end 排序结束位置*/public static void quickSort(int[] arr, int begin, int end) {// 递归终止条件:起始位置大于等于结束位置if (begin >= end) {return;}int pivot = arr[begin]; // 选择基准元素,默认以第一个元素为基准int left = begin + 1; // 左边起始位置int right = end; // 右边结束位置while (left <= right) {/*** 在左边找到第一个大于基准元素的位置* 注意:这里要先判断left <= right,否则会导致索引越界*/while (left <= right && arr[left] <= pivot) {left++;}/*** 在右边找到第一个小于基准元素的位置* 注意:这里要先判断left <= right,否则会导致索引越界*/while (left <= right && arr[right] >= pivot) {right--;}// 如果左指针仍在右指针左边,则交换左、右指针所指的元素if (left < right) {swap(arr, left, right);}}// 将基准元素交换到正确的位置,即左指针所在位置swap(arr, begin, right);// 对左边部分进行快速排序quickSort(arr, begin, right - 1);// 对右边部分进行快速排序quickSort(arr, right + 1, end);}/*** 交换数组中两个元素的位置* @param arr 数组* @param i 第一个元素的索引* @param j 第二个元素的索引*/public static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
5.归并排序
归并排序,简单的说把一串数,从中平等分为两份,再把两份再细分,直到不能细分为止,这就是分而治之的分的步骤. 再从最小的单元,两两合并,合并的规则是将其按从小到大的顺序放到一个临时数组中,再把这个临时数组替换原数组相应位置
import java.util.Arrays;
/**
-
归并排序:
-
归并操作的工作原理如下:
-
第一步:申请空间,使其大小为两个已经 排序序列之和,该空间用来存放合并后的序列
-
第二步:设定两个 指针,最初位置分别为两个已经排序序列的起始位置
-
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置重复步骤3直到某一指针超出序列尾
-
将另一序列剩下的所有元素直接复制到合并序列尾
*
*/
public class MergeSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组mergeSort(arr, 0, arr.length - 1); // 调用归并排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}/*** 归并排序方法* @param a 待排序的数组* @param s 排序起始位置* @param e 排序结束位置*/public static void mergeSort(int[] a, int s, int e) {if (s < e) {int m = (s + e) / 2; // 找到数组的中间位置mergeSort(a, s, m); // 递归调用对左边部分进行归并排序mergeSort(a, m + 1, e); // 递归调用对右边部分进行归并排序merge(a, s, m, e); // 合并左右两个有序数组}}/*** 合并左右两个有序数组* @param a 原始数组* @param s 左数组起始位置* @param m 左数组结束位置* @param e 右数组结束位置*/private static void merge(int[] a, int s, int m, int e) {int[] temp = new int[e - s + 1]; // 临时数组用来存放合并后的结果int l = s; // 左数组的起始位置int r = m + 1; // 右数组的起始位置int i = 0; // 临时数组的索引// 比较左右两个数组中的元素,将较小的元素放入临时数组中while (l <= m && r <= e) {if (a[l] < a[r]) {temp[i++] = a[l++];} else {temp[i++] = a[r++];}}// 将左数组中剩余的元素放入临时数组中while (l <= m) {temp[i++] = a[l++];}// 将右数组中剩余的元素放入临时数组中while (r <= e) {temp[i++] = a[r++];}// 将临时数组中的元素覆盖原始数组中的元素,完成排序for (int n = 0; n < temp.length; n++) {a[s + n] = temp[n];}}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
6.希尔排序
当数组规模较大时,插入排序的效率较低。希尔排序(Shell Sort)是一种插入排序的改进算法,通过将相隔一定间隔的元素进行分组,对每个分组进行插入排序,逐步缩小间隔,最终完成排序。
具体步骤如下:
1. 首先,选定一个初始的间隔值(称为步长),通常将数组长度的一半作为初始值。
2. 根据选定的步长,将数组分成若干个分组。
3. 对每个分组进行插入排序,即将每个分组中的元素按照插入排序的方式进行排序。
4. 缩小步长,继续第2和第3步操作,直到步长为1。
5. 当步长为1时,进行最后一次插入排序,此时数组已经基本有序,插入排序的效率会很高。
希尔排序的关键在于选定合适的步长和分组方式。常用的步长序列有希尔原始提出的递减系列(n/2, n/4, n/8...),以及Hibbard系列(2^k - 1, 2^(k-1) - 1...),Sedgewick系列等。
希尔排序的时间复杂度与步长序列的选取有关,最好的情况下为O(n^(3/2)),平均情况下为O(nlogn)。希尔排序是一种不稳定的排序算法,即相同元素的相对顺序在排序后可能发生变化。
希尔排序相对于插入排序来说,虽然没有改变算法的基本思想,但通过拆分成多个子序列进行插入排序,大大提高了排序的效率。
import java.util.Arrays;public class ShellSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组shellSort(arr); // 调用希尔排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}/*** 希尔排序方法* @param arr 待排序的数组*/public static void shellSort(int[] arr) {int gap = arr.length / 2; // 初始步长int k = 1; // 记录排序轮数// 根据步长进行分组,对每个分组进行插入排序while (gap > 0) {// 对每个分组进行插入排序for (int i = gap; i < arr.length; i++) {// 对当前分组的元素进行插入排序for (int j = i - gap; j >= 0; j -= gap) {if (arr[j] > arr[j + gap]) {// 如果前一个元素大于后一个元素,则进行交换int temp = arr[j];arr[j] = arr[j + gap];arr[j + gap] = temp;}}}System.out.println("第" + k++ + "轮排序结果:" + Arrays.toString(arr));gap /= 2; // 缩小步长}}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
[5, 1, 0, 7, 4, 9, 3, 2, 8, 6]
[0, 1, 3, 2, 4, 6, 5, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
7.基数排序
基数排序(Radix Sort)是一种非比较性的稳定排序算法,它将整数按照每个位上的数字进行排序,可以根据位数进行排序,依次按个位、十位、百位...从低位到高位进行排序。基数排序适用于排序非负整数或具有相同位数的正整数序列。
具体步骤如下:
1. 找到数组中的最大值,并确定最大值的位数,作为排序的轮数。
2. 从个位开始,根据当前位上的数字将元素分配到对应的桶中。
3. 按照分配的顺序重新排列数组。
4. 继续处理十位、百位...直到处理完最高位,完成排序。
基数排序要求具备一定的稳定性,即在同一位上相同数字的先后顺序不发生改变。
以下是带有详细注释的基数排序的Java代码示例:```java
import java.util.*;public class RadixSort {public static void radixSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}// 获取数组中的最大值int max = Arrays.stream(arr).max().getAsInt();// 计算最大值的位数,决定排序的轮数int exp = 1;while (max / exp > 0) {countingSort(arr, exp);exp *= 10;}}// 对数组按照某一位上的值进行计数排序private static void countingSort(int[] arr, int exp) {int n = arr.length;int[] output = new int[n];int[] count = new int[10];// 统计该位上每个数字的出现次数for (int num : arr) {count[(num / exp) % 10]++;}// 将计数数组转换为位置索引数组for (int i = 1; i < 10; i++) {count[i] += count[i - 1];}// 按照该位上的值将元素放入output数组中for (int i = n - 1; i >= 0; i--) {output[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}// 将排序好的数组赋值给原数组System.arraycopy(output, 0, arr, 0, n);}public static void main(String[] args) {int[] arr = {170, 45, 75, 90, 802, 24, 2, 66};System.out.println("排序前:" + Arrays.toString(arr));radixSort(arr);System.out.println("排序后:" + Arrays.toString(arr));}
}这段代码实现了带有详细注释的基数排序算法。在基数排序过程中,首先找到数组中的最大值,然后逐个按位进行计数排序。最后,将排序好的数组赋值给原数组。基数排序的时间复杂度为O(d*(n+b)),其中d为最大值的位数,n为数组长度,b为基数(这里是10)。基数排序是一种稳定的排序算法,适用于整数排序。
运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
8.堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点
堆排序(Heap Sort)是一种基于完全二叉树数据结构——堆的排序算法,它利用堆的性质进行排序。堆排序首先将待排序的元素构建成一个最大堆(或最小堆),然后将堆顶元素与堆尾元素交换,调整剩余元素重新构建堆,重复这个过程直到所有元素都有序。堆排序的时间复杂度为O(nlogn),具有原址排序的特点,是不稳定排序算法。
具体步骤如下:
1. 构建最大堆(大顶堆):从最后一个非叶子节点开始,向上逐个调整节点,保证父节点的值大于等于子节点的值。
2. 调整堆:交换堆顶元素与最后一个元素,然后将剩余元素重新构建最大堆。
3. 重复步骤2,直到所有元素有序。
4. 如果要实现升序排序,则采用大顶堆;如果要实现降序排序,则采用小顶堆。
以下是带有详细注释的堆排序的Java代码示例:```java
public class HeapSort {public static void heapSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}int n = arr.length;// 构建最大堆for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}// 调整堆结构,交换堆顶元素与末尾元素for (int i = n - 1; i >= 0; i--) {// 交换堆顶元素和末尾元素int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 调整堆heapify(arr, i, 0);}}// 调整堆private static void heapify(int[] arr, int n, int i) {int largest = i; // 最大元素的下标int left = 2 * i + 1; // 左子节点下标int right = 2 * i + 2; // 右子节点下标// 左子节点大于根节点if (left < n && arr[left] > arr[largest]) {largest = left;}// 右子节点大于根节点if (right < n && arr[right] > arr[largest]) {largest = right;}// 如果最大元素不是根节点,交换根节点和最大元素if (largest != i) {int temp = arr[i];arr[i] = arr[largest];arr[largest] = temp;// 继续调整堆heapify(arr, n, largest);}}public static void main(String[] args) {int[] arr = {12, 11, 13, 5, 6, 7};System.out.println("排序前:" + Arrays.toString(arr));heapSort(arr);System.out.println("排序后:" + Arrays.toString(arr));}
}
```
这段代码实现了带有详细注释的堆排序算法。在堆排序过程中,首先构建最大堆,然后将堆顶元素与末尾元素交换,调整剩余元素重新构建最大堆。重复这个过程直到所有元素有序。堆排序的时间复杂度为O(nlogn),是一种高效的排序算法。
运行结果
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
各种算法的比较

归并排序空间复杂度是O(n)
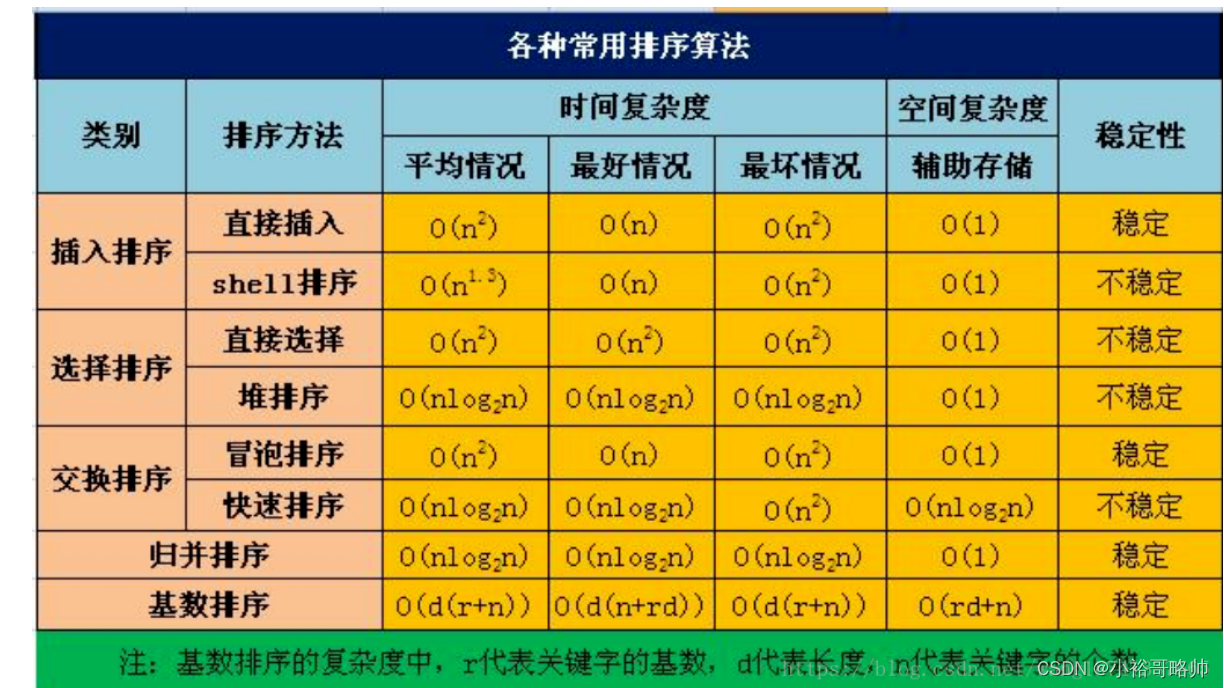
速度: 快速排序>>归并排序>>>>>插入排序>>选择排序>>冒泡排序
并且可以看到,选择排序,冒泡排序在数据量越来越大的情况下,耗时已经呈指数型上涨,而不是倍数上涨
(1)若n较小(如n≤50),可采用直接插入或直接选择排序。
当记录规模较小时,直接插入排序较好;否则因为直接选择移动的记录数少于直接插人,应选直接选择排序为宜。
(2)若文件初始状态基本有序(指正序),则应选用直接插人、冒泡或随机的快速排序为宜;
(3)若n较大,则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序或归并排序。
快速排序是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的。
若要求排序稳定,则可选用归并排序。
相关文章:

常见的排序算法整理
1.冒泡排序 1.1 冒泡排序普通版 每次冒泡过程都是从数列的第一个元素开始,然后依次和剩余的元素进行比较,若小于相邻元素,则交换两者位置,同时将较大元素作为下一个比较的基准元素,继续将该元素与其相邻的元素进行比…...

stm32——hal库学习笔记(定时器)
这里写目录标题 一、定时器概述(了解)1.1,软件定时原理1.2,定时器定时原理1.3,STM32定时器分类1.4,STM32定时器特性表1.5,STM32基本、通用、高级定时器的功能整体区别 二、基本定时器࿰…...

方法鉴权:基于 Spring Aop 的注解鉴权
在Spring框架中,可以使用面向切面编程(AOP)来实现注解鉴权。这通常涉及到定义一个切面(Aspect),该切面会在方法执行前进行拦截,并根据注解value值来决定是否允许执行该方法。 简单思路…...

多模态相关论文笔记
(cilp) Learning Transferable Visual Models From Natural Language Supervision 从自然语言监督中学习可迁移的视觉模型 openAI 2021年2月 48页 PDF CODE CLIP(Contrastive Language-Image Pre-Training)对比语言图像预训练模型 引言 它比ImageNet模型效果更好,…...

maven 打包命令
Maven是基于项目对象模型(POM project object model),可以通过一小段描述信息(配置)来管理项目的构建,报告和文档的软件项目管理工具。 Maven的核心功能便是合理叙述项目间的依赖关系,通俗点讲,就是通过po…...
)
开源模型应用落地-业务优化篇(六)
一、前言 经过线程池优化、请求排队和服务实例水平扩容等措施,整个AI服务链路的性能得到了显著地提升。但是,作为追求卓越的大家,绝不会止步于此。我们的目标是在降低成本和提高效率方面不断努力,追求最佳结果。如果你们在实施AI项目方面有经验,那一定会对GPU服务器的高昂…...

编程笔记 Golang基础 015 数据类型:布尔类型
编程笔记 Golang基础 015 数据类型:布尔类型 在Go语言中,布尔类型(bool)是一种基本数据类型,用于表示逻辑值,即真或假、是或否的情况。它主要用于条件判断和逻辑运算。 定义与取值: Go语言中的布…...
腾讯云OSS文件上传功能
腾讯云COS介绍 腾讯云COS(Cloud Object Storage)是一种基于对象的存储服务,用于存储和管理海量的非结构化数据,如图片、音视频文件、备份数据等。它具有以下特点和优势: 高可靠性:采用分布式存储架构&…...

2023 re:Invent 用 PartyRock 10 分钟构建你的 AI 应用
前言 一年一度的亚马逊云科技的 re:Invent 可谓是全球云计算、科技圈的狂欢,每次都能带来一些最前沿的方向标,这次也不例外。在看完一些 keynote 和介绍之后,我也去亲自体验了一些最近发布的内容。其中让我感受最深刻的无疑是 PartyRock 了。…...
如何使用idea连接服务器上的mysql?
安全组进行开放 具体步骤 关闭防火墙 开放端口号 重启防火墙 firewall-cmd --reload在mysql进行修改配置 update user set host % where user root;flush privileges;使得其他网络也可以连接这个数据库 另外如果想要sqlyog或者其他图形化界面要连接到数据库可以看下面这…...
主流开发语言和开发环境介绍
主流开发语言和开发环境介绍文章目录 ⭐️ 主流开发语言:2024年2月编程语言排行榜(TIOBE前十)⭐️ 主流开发语言开发环境介绍1.Python1.1 **IDLE**1.2 **PyCharm**1.3 **Anaconda**1.4 **Jupyter Notebook**1.5 **Sublime Text** 2.C2.1 **De…...

samber/lo 库的使用方法: 处理 channel
samber/lo 库的使用方法: 处理 channel samber/lo 是一个 Go 语言库,提供了一些常用的集合操作函数,如 Filter、Map 和 FilterMap。汇总目录页面 这个库函数太多,因此我决定按照功能分别介绍,本文介绍的是 samber/lo…...

铌酸锂芯片与精密划片机:科技突破引领半导体制造新潮流
在当今快速发展的半导体行业中,一种结合了铌酸锂芯片与精密划片机的创新技术正在崭露头角。这种技术不仅引领着半导体制造领域的进步,更为其他产业带来了前所未有的变革。 铌酸锂芯片是一种新型的微电子芯片,它使用铌酸锂作为基底材料&#x…...
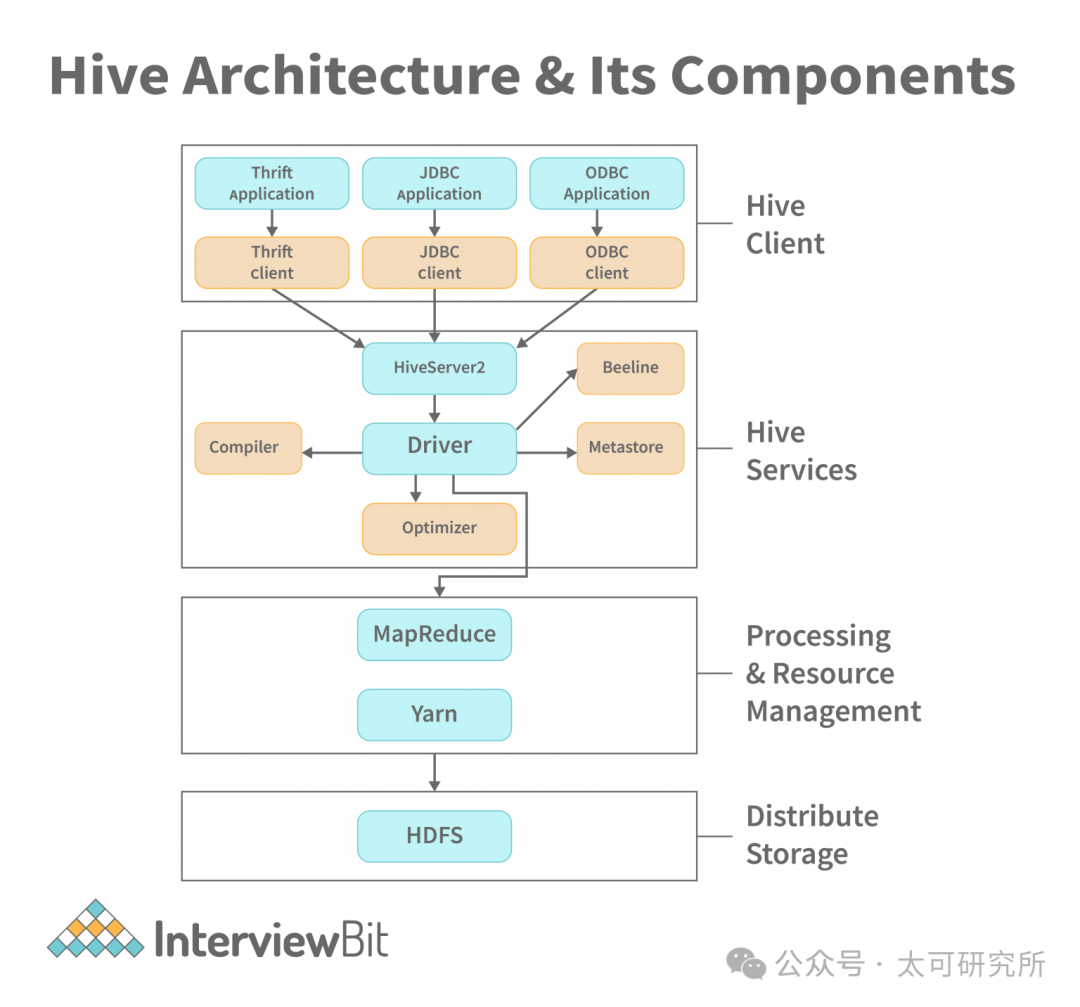
大数据计算技术秘史(上篇)
在之前的文章《2024 年,一个大数据从业者决定……》《存储技术背后的那些事儿》中,我们粗略地回顾了大数据领域的存储技术。在解决了「数据怎么存」之后,下一步就是解决「数据怎么用」的问题。 其实在大数据技术兴起之前,对于用户…...
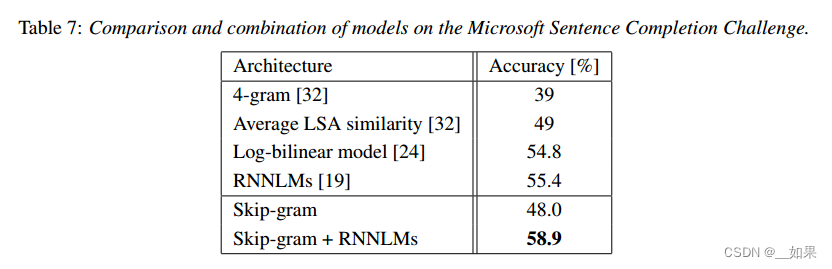
论文精读--word2vec
word2vec从大量文本语料中以无监督方式学习语义知识,是用来生成词向量的工具 把文本分散嵌入到另一个离散空间,称作分布式表示,又称为词嵌入(word embedding)或词向量 Abstract We propose two novel model architec…...

Android13 针对low memory killer内存调优
引入概念 在旧版本的安卓系统中,当触发lmk(low memory killer)的时候一般认为就是内存不足导致,但是随着安卓版本的增加lmk的判断标准已经不仅仅是内存剩余大小,io,cpu同样会做评判,从而保证设备…...
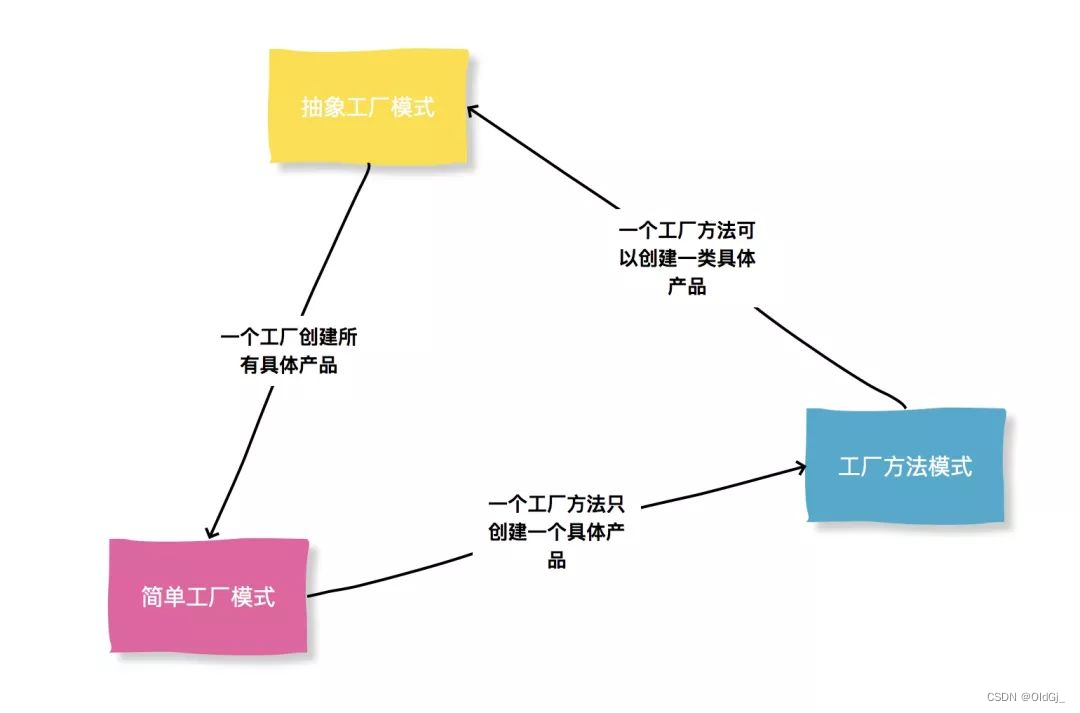
【深入理解设计模式】 工厂设计模式
工厂设计模式 工厂设计模式是一种创建型设计模式,它提供了一种在不指定具体类的情况下创建对象的接口。在工厂设计模式中,我们定义一个创建对象的接口,让子类决定实例化哪一个类。工厂方法使一个类的实例化延迟到其子类。 工厂设计模式的目…...
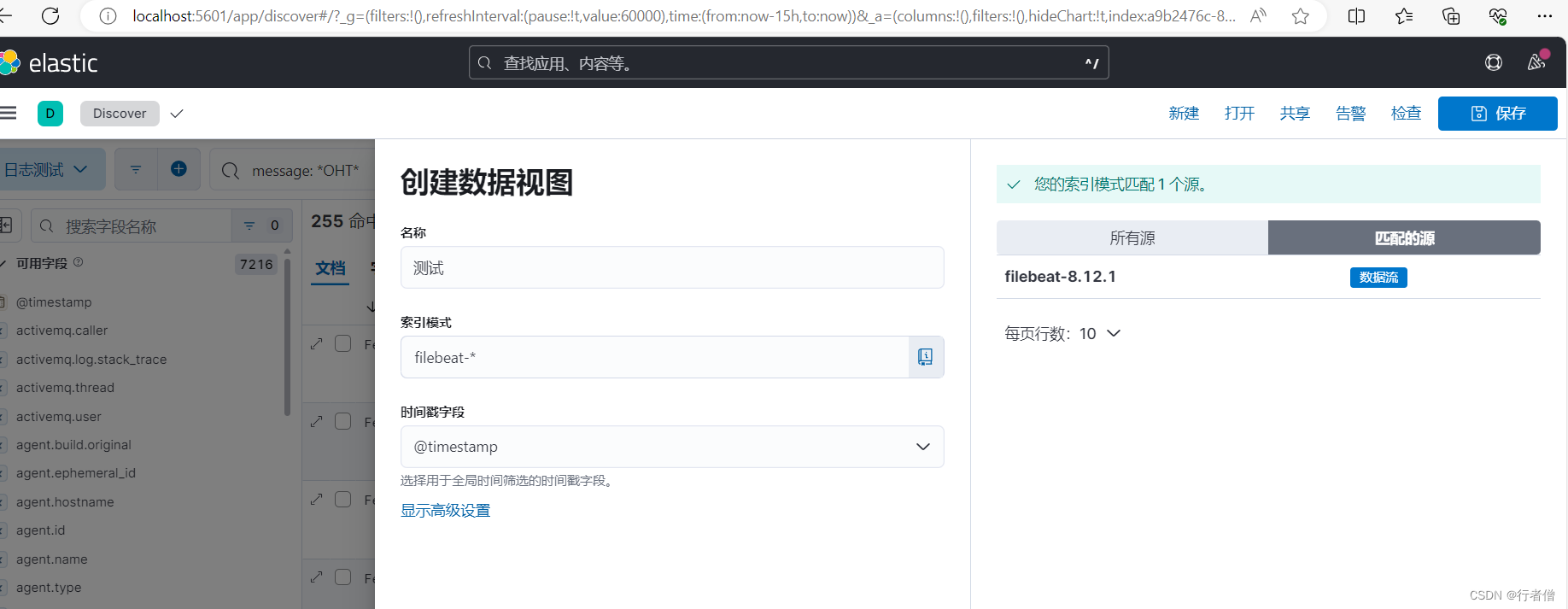
Windows下搭建EFK实例
资源下载 elasticSearch :下载最新版本的就行 kibana filebeat:注意选择压缩包下载 更新elasticsearch.yml,默认端口9200: # Elasticsearch Configuration # # NOTE: Elasticsearch comes with reasonable defaults for most …...
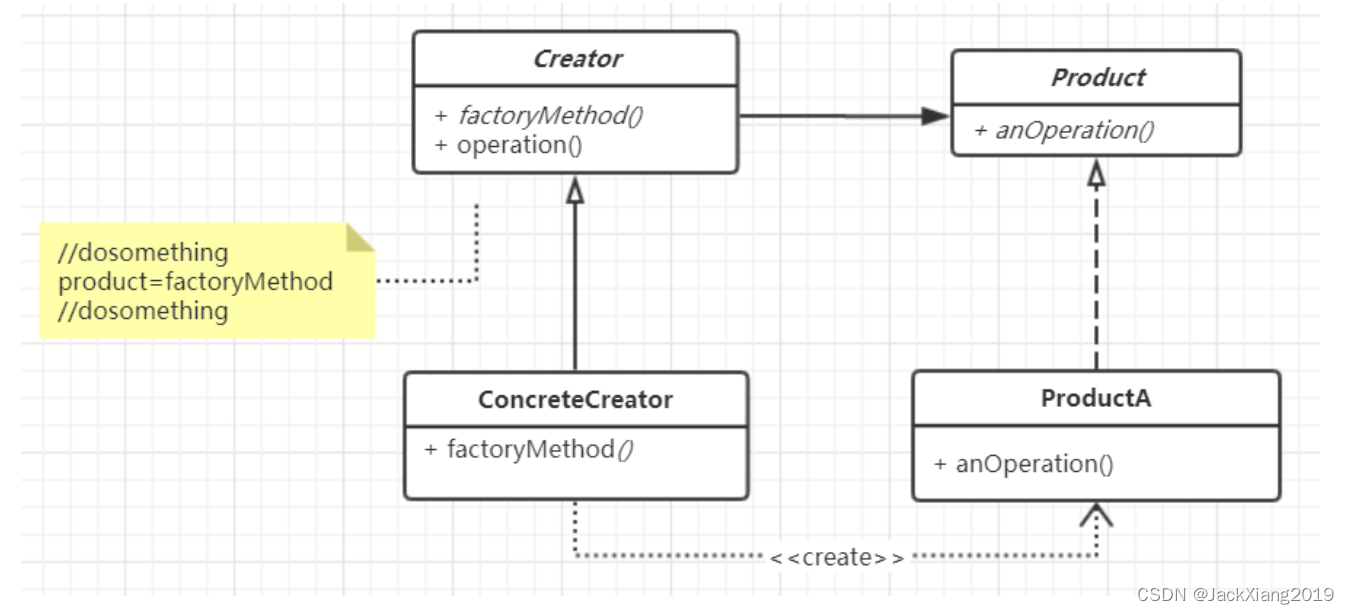
工厂方法模式Factory Method
1.模式定义 定义一个用于创建对象的接口,让子类决定实例化哪一个类。Factory Method 使得一个类的实例化延迟到子类 2.使用场景 1.当你不知道改使用对象的确切类型的时候 2.当你希望为库或框架提供扩展其内部组件的方法时 主要优点: 1.将具体产品和创建…...

Vue的个人笔记
Vue学习小tips ctrl s ----> 运行 alt b <scrip> 链接 <script src"https://cdn.jsdelivr.net/npm/vue2.7.16/dist/vue.js"></script> 插值表达式 指令...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
