备战蓝桥杯---动态规划(应用2(一些十分巧妙的优化dp的手段))
好久不见,甚是想念,最近一直在看过河这道题(感觉最近脑子有点宕机QAQ),现在算是有点懂了,打算记录下这道又爱又恨的题。(如有错误欢迎大佬帮忙指出)
话不多说,直接看题:

类比分组背包,我们可以令f[i][j]表示前i个数能否组成j.
转移方程为:f[i][j]=f[i-1][j-x1^2]||f[i-1][j-x2^2]||....||f[i-1][j-xi^2]
现在我们考虑优化一下:
因为f[i][j]为bool类型,我们可以尝试用bitset优化一下。
我们每一行用bitset,然后用位运算实现(比正常平移优化约32倍)
f[i]=f[i-1]||f[i-1]<<(x[i]^2);(注意bitset最低位在最右边)
下面为AC代码:
#include<bits/stdc++.h>
using namespace std;
int n;
bitset<1000100> f[110];
int main(){cin>>n;f[0][0]=1;for(int i=1;i<=n;i++){int l,r;scanf("%d%d",&l,&r);for(int k=l;k<=r;k++){f[i]|=f[i-1]<<(k*k);}}cout<<f[n].count();
}接题:

类似爬楼梯,我们记f[i]为到i时最少踩的个数。如果,f[i]上有石子,那么f[i]=min(f[i-j])+1(j>=s&&j<=t).然后一看范围,空间与时间都不允许。
我们应该还记得上次背包用map存的情况,这是因为空间上有大量的冗余。
而在这一题上,我们发现相比于桥,石子特别小,也说明他们间的距离非常大.
于是我们进行状态压缩。
从这开始就困了我蛮久(还是自己太菜了QAQ)
首先按照上述过程我们顺利过了30,我们不妨先用自己测试输出一下具体的样子。
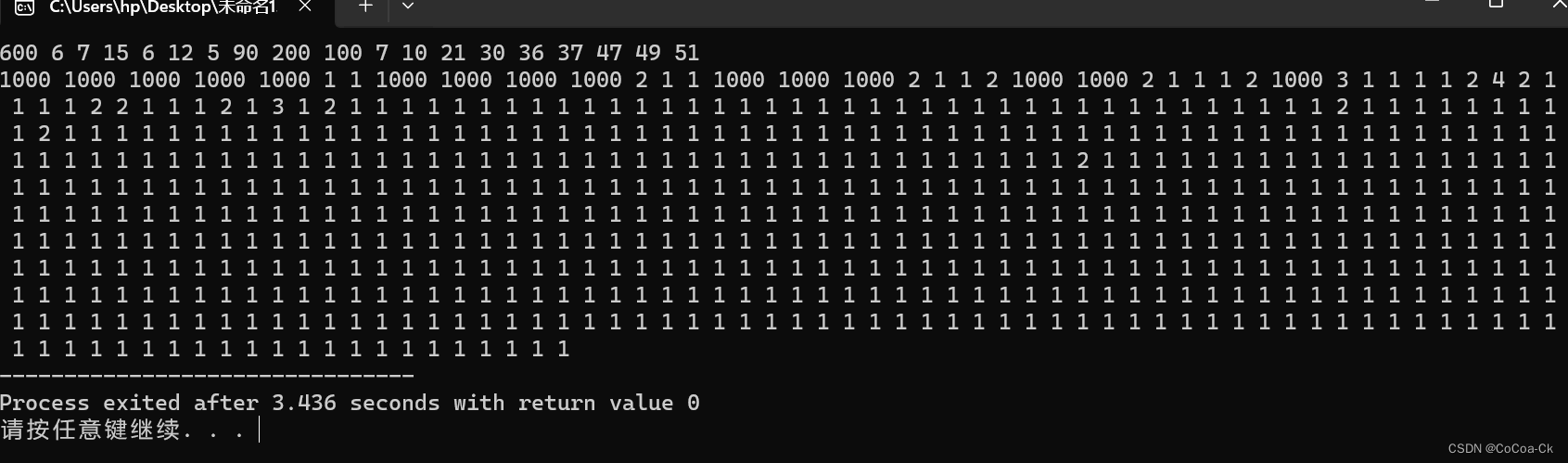
我们发现如果两个石子距离十分大,从某一个位置开始,dp的值都一样。
比赛时,直接压缩成一个不超范围的直接提交(如果是我的话,就直接赋一个2024)
当然,虽然规律很明显,但对于有”强迫症“的我来说还是有点难以接受,于是我们从感性与严格证明的角度来论证正确性。
我们不妨自己先画个数轴,我们以6/7举例。

很显然,越到后面,每一段逐渐重合,然后就连续了,因为没有石子,假设某一段的dp值不同(假设有3个不同的值),那么到了后面,对于每一个点,他的状态势必是在<=3个的不同的值里选min的,而3个不同的值中势必有最小的一个,越到后面,除了最小的其他2个一定会在过程中慢慢被舍弃,最终收敛于最小的值(当然,可能有无法到达的)。
总结一下,当两个石子离得比较远,那在中间的这一段,其实就是在经过上一个石子的更新后去不断地筛选出min然后就不变了,而我们要做的就是把不变的一段删掉)
可能有点抽象,那么我们来严格证一下:
首先,我们得知道一个结论:
在离一点oS(S−1)的位置其每一点都可以到(等会证)
然后请看分析:

因此,我们推出一个结论:
在离一点oS(S−1)的位置其每一点都可以到并且他们的dp值都一样。
接下来,我们就得到了压缩方法:
如果两个石子距离>s(s-1),那么就把他变成s(s-1),这样就可以顺利通过了(注意,虽然这样石子后面的几个位置可能不准确,但是不妨碍求min的正确性,保险一点,可以再多空格,这样子每一个点的dp都是对的了)。
下面是对那个数学结论的证明:
我看网上很多是用Bezout's identity来证,我在这采用比较直观的方法(这里证s^2,比较粗略):

下面给出AC代码(注意s==t的情况):
#include<bits/stdc++.h>
using namespace std;
int l,s,t,m,ck[110],dp[100000],ze[110];
map<int,int> mp;
bool cmp(int a,int b){return a<b;
}
int main(){cin>>l>>s>>t>>m;memset(dp,0x3f,sizeof(dp));for(int i=1;i<=m;i++) scanf("%d",&ck[i]);if(s==t){int cnt=0;for(int i=1;i<=m;i++){if(ck[i]%s==0) cnt++;}cout<<cnt;return 0;}sort(ck+1,ck+m+1,cmp);int mm=s*s+10;ze[0]=0;for(int i=1;i<=m;i++){ze[i]=min(mm,ck[i]-ck[i-1])+ze[i-1];mp[ze[i]]=1;}ze[m+1]=min(mm,l-ck[m])+ze[m];dp[0]=0;for(int i=1;i<=ze[m+1]+t-1;i++){for(int j=s;j<=t;j++){if(i-j>=0){if(mp.count(i)==1) dp[i]=min(dp[i],1+dp[i-j]);else dp[i]=min(dp[i],dp[i-j]);}}}int ans=1000;for(int i=ze[m+1];i<=ze[m+1]+t-1;i++) ans=min(ans,dp[i]);cout<<ans;
}相关文章:

备战蓝桥杯---动态规划(应用2(一些十分巧妙的优化dp的手段))
好久不见,甚是想念,最近一直在看过河这道题(感觉最近脑子有点宕机QAQ),现在算是有点懂了,打算记录下这道又爱又恨的题。(如有错误欢迎大佬帮忙指出) 话不多说,直接看题&…...

从 git 分支中合并特定文件,而不是整个分支的内容
问题 在git 中,我们可以使用 git merge 命令,合并整个分支,覆盖当前分支的内容,但是有时候我们并不想这么做,而是想 merge 某个文件。那么下面提供两种办法。 方法一 使用 git checkout,从别的分支&#x…...
pycharm 远程运行报错 Failed to prepare environment
什么也没动的情况下,远程连接后运行是没问题的,突然在运行时就运行不了了,解决方案 清理缓存: 有时候 PyCharm 的内部缓存可能出现问题,可以尝试清除缓存(File > Invalidate Caches / Restart࿰…...

(十二)【Jmeter】线程(Threads(Users))之setUp 线程组
简述 操作路径如下: 作用:在正式测试开始前执行预加载或预热操作,为测试做准备。配置:设置预加载或预热操作的采样器、循环次数等参数。使用场景:确保在正式测试开始前应用程序已经达到稳定状态,减少测试结果的偏差。优点:提供预加载或预热操作,确保测试的准确性。缺…...

代码随想录算法训练营第二十五天|216.组合总和III,17.电话号码的字母组合
目录 216.组合总和II 17.电话号码的字母组合 216.组合总和II 如果把 组合问题理解了,本题就容易一些了。 题目链接/文章讲解:代码随想录 视频讲解:和组合问题有啥区别?回溯算法如何剪枝?| LeetCode:216.…...
c#创建安装windows服务
背景:最近在做设备数据对接采集时,遇到一些设备不是标准的Service-Client接口,导致采集的数据不够准确;比如设备如果中途开关机后,加工的数量就会从0开始重新计数,因此需要实时监控设备的数据,进行叠加处理;考略到工厂设备比较多,实时监听接口的数据为每秒3次,因此将…...

【JVM】打破双亲委派机制
📝个人主页:五敷有你 🔥系列专栏:JVM ⛺️稳中求进,晒太阳 打破双亲委派机制 打破双亲委派机制三种方法 自定义类加载器 ClassLoader包含了四个核心方法 //由类加载器子类实现,获取二进制数据调用…...

程序员要了解的AI基本知识
一.AI从业人员的三个层次 AI从业人员的层次是不同的,所以需要的知识面也是不同的。下面大致给出了3个层面。 1.学术研究者 他们的工作是从理论上诠释机器学习的各个方面,试图找出“这样设计模型/参数为什么效果更好”,并且为其他从业者提供…...
306_C++_QT_创建多个tag页面,使用QMdiArea容器控件,每个页面都是一个新的表格[或者其他]页面
程序目的是可以打开多个styles文件(int后缀文件),且是tag样式的(就是可以切多个页面出来,并且能够单独关闭);其中读取ini文件,将其插入到表格中的操作,也是比较复杂的,因为需要保持RGB字符串和前面的说明字符串对齐 ini文件举例: [MainMenu] Foreground\Selected=&…...

OpenCV笔记3:级联分类器实现人脸检测+绘制logo
OpenCV 人脸检测绘制logo 检测人脸绘制人脸区域绘制logo 寻找轮廓 二值图阈值 绘制轮廓 """ 绘制logo 1. 检测人脸区域如何检测到人脸眼睛、鼻子、嘴巴、眉毛、下巴等级联的过程OpenCV、Mediapipe、YOLOFace、DBFace等 2. 把logo粘贴在人脸上方 ""…...
)
python---Pixiv排行榜图片获取(2024.2.16)
1.提示: 使用需要安装各种import的包,都是很基础的包,直接安装即可。 自备梯子 。 切记把userid和cookie改为自己账号的参数! userid就是点击pixiv头像,网址后面一串数, cookie是打开排行榜后,…...
QT3作业
1 2. 使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数,将登录按钮使用t5版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin"&#…...

零基础,两个月,如何蓝桥杯备战?
本文约4000字,阅读时长8~12分钟。 首先说明,目前0算法基础,想在两个月后的蓝桥杯拿奖,有一定难度,但也不是完全没可能。在这么短的时间内选择正确的方法,做高性价比的事就尤为重要。 我是蓝桥云课省赛无忧…...
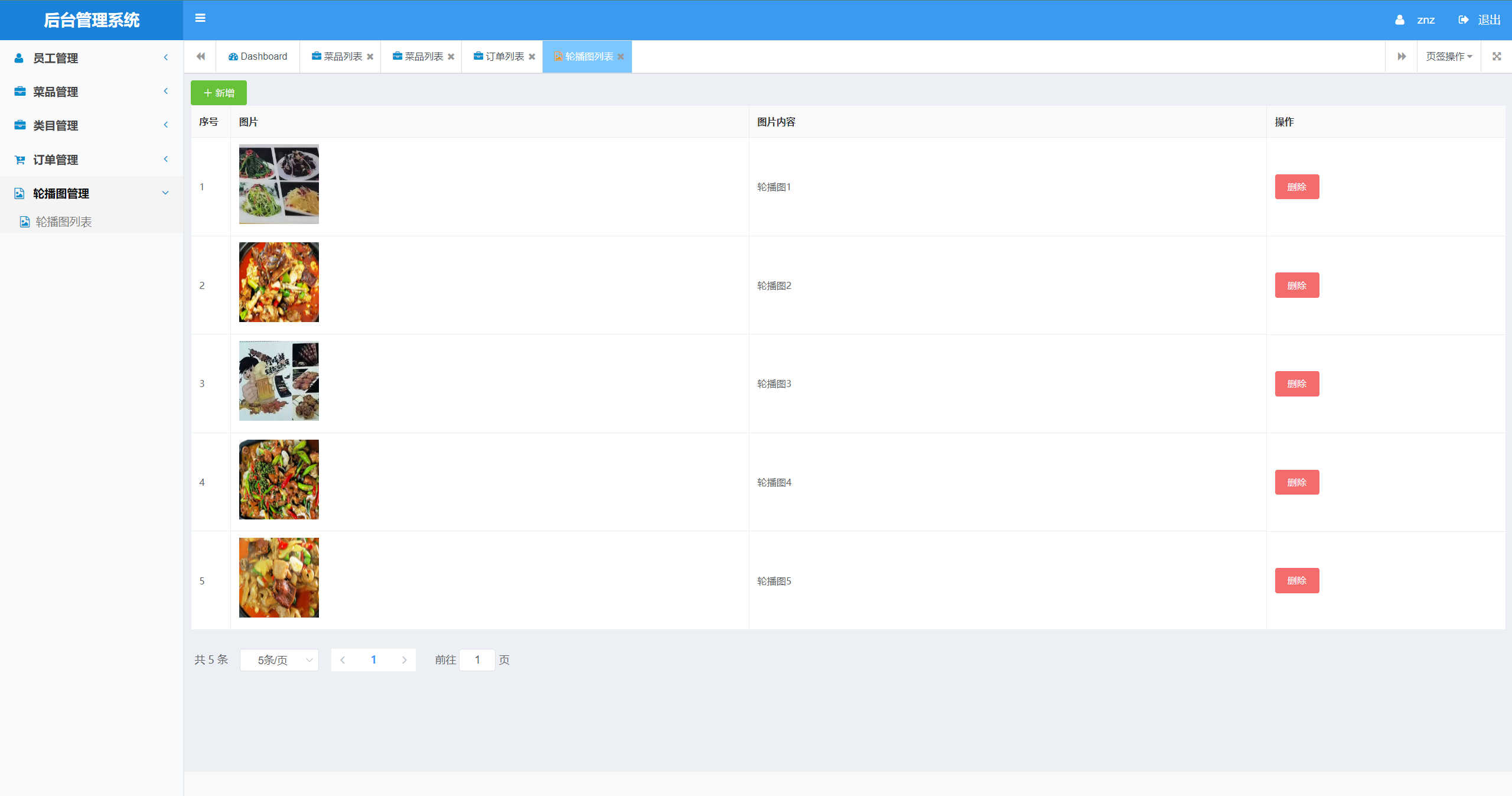
基于Java+小程序点餐系统设计与实现(源码+部署文档)
博主介绍: ✌至今服务客户已经1000、专注于Java技术领域、项目定制、技术答疑、开发工具、毕业项目实战 ✌ 🍅 文末获取源码联系 🍅 👇🏻 精彩专栏 推荐订阅 👇🏻 不然下次找不到 Java项目精品实…...

炫酷3D按钮
一.预览 该样式有一种3D变换的高级感,大家可以合理利用这些样式到自己的按钮上 二.代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice…...

世界顶级名校计算机专业学习使用教材汇总
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-IauYk2cGjEyljid0 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...

通过ffmpeg实现rtsp rtmp rtmps 推流
安卓端推流直接引用 implementation com.arthenica:mobile-ffmpeg-full:4.4 包 记得添加网络权限 <uses-permission android:name"android.permission.INTERNET" /> 基本方法: public static long executionId; Override protected void onCr…...

基于springboot+vue的高校学科竞赛系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...
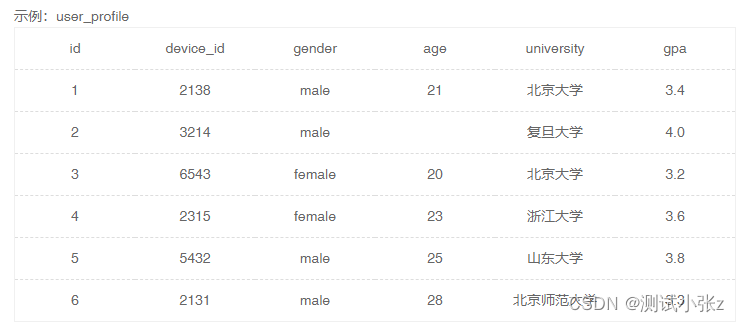
SQL 练习题目(入门级)
今天发现了一个练习SQL的网站--牛客网。里面题目挺多的,按照入门、简单、中等、困难进行了分类,可以直接在线输入SQL语句验证是否正确,并且提供了测试表的创建语句,也可以方便自己拓展练习,感觉还是很不错的一个网站&a…...
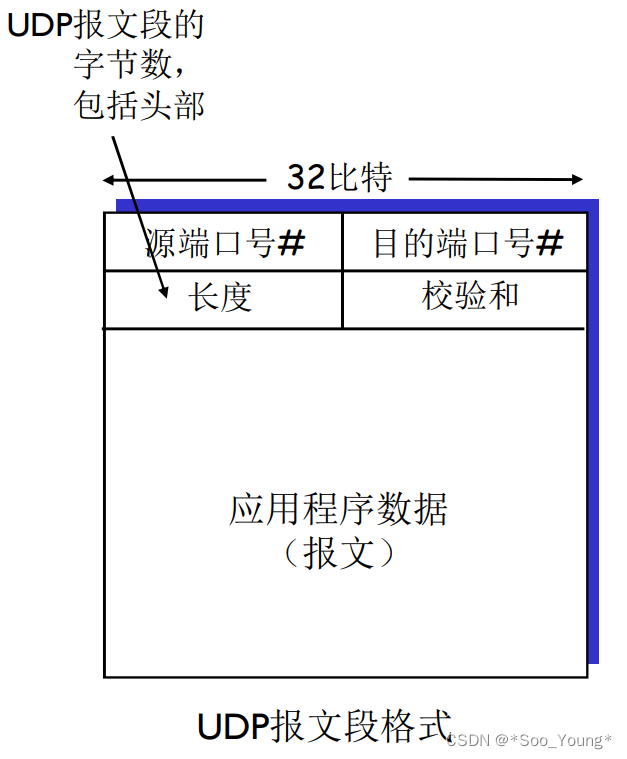
中科大计网学习记录笔记(十四):多路复用与解复用 | 无连接传输:UDP
前言: 学习视频:中科大郑烇、杨坚全套《计算机网络(自顶向下方法 第7版,James F.Kurose,Keith W.Ross)》课程 该视频是B站非常著名的计网学习视频,但相信很多朋友和我一样在听完前面的部分发现信…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
