蒙特卡洛树搜索(MTCS)
一、目标
一种启发式的搜索算法,在搜索空间巨大的场景下比较有效
算法完成后得到一棵树,这棵树可以实现:给定一个游戏状态,直接选择最佳的下一步
二、算法四阶段
1、选择(Selection)
父节点选择UCB值最大的子节点作为当前节点
UCB=Vi‾+c2lnNniUCB=\overline{V_{i}} +c\sqrt{\frac{2lnN}{n_{i}}} UCB=Vi+cni2lnN
其中,c通常取2。
nin_{i}ni代表 iii 节点被选择的次数,NNN代表其父节点被选择的次数。
Vi‾\overline{V_{i}}Vi 代表 iii 节点的平均价值大小(例如 iii 节点 Vi=v,ni=3V_{i}=v,n_{i}=3Vi=v,ni=3,则Vi‾=v/3\overline{V_{i}}=v/3Vi=v/3)。
2、扩展(Expansion)
为当前节点创建一个或多个子节点(子节点代表当前节点下可采取的动作)
3、仿真(Simulation/Rollout)
在某一节点用随机策略进行模拟(rollout)
def Rollout(S_i): # S_i = 当前状态While True: # S_i达到终止条件/状态(下棋中某方获胜或平局)if S_i a terimal state: # 返回结果valuereturn value(S_i) # 还未终止,则# 随机选择一个当前状态下的可用动作A_i = random(available_action(S_i)) # 在当前状态下采取动作,得到新的状态S_i = simulate(A_i, S_i)
4、反向传播(Backpropagation)
得到模拟结果后不断反向更新父节点
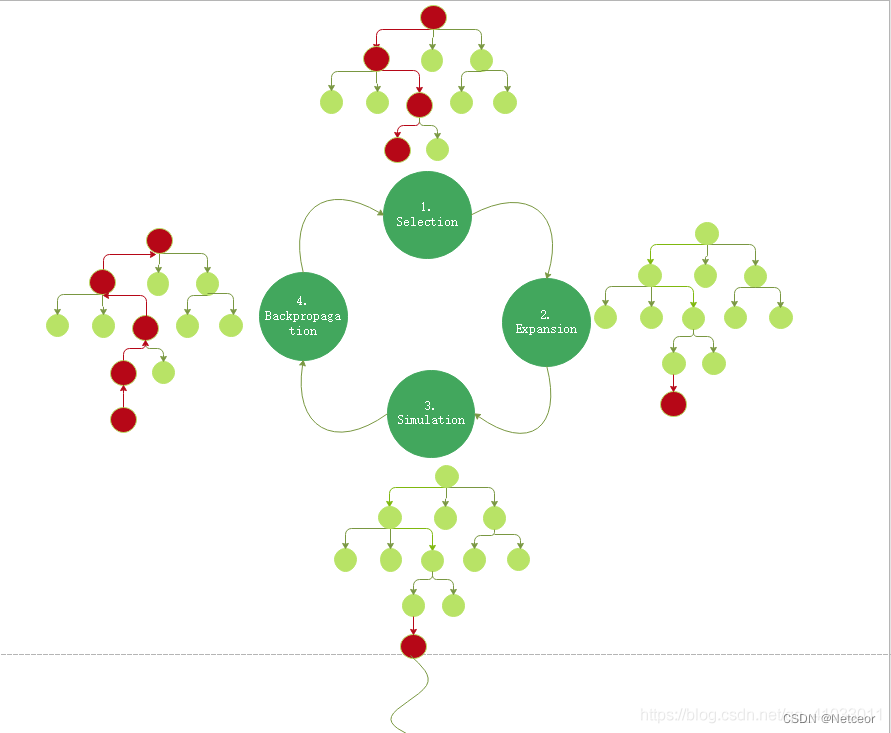
三、运行过程
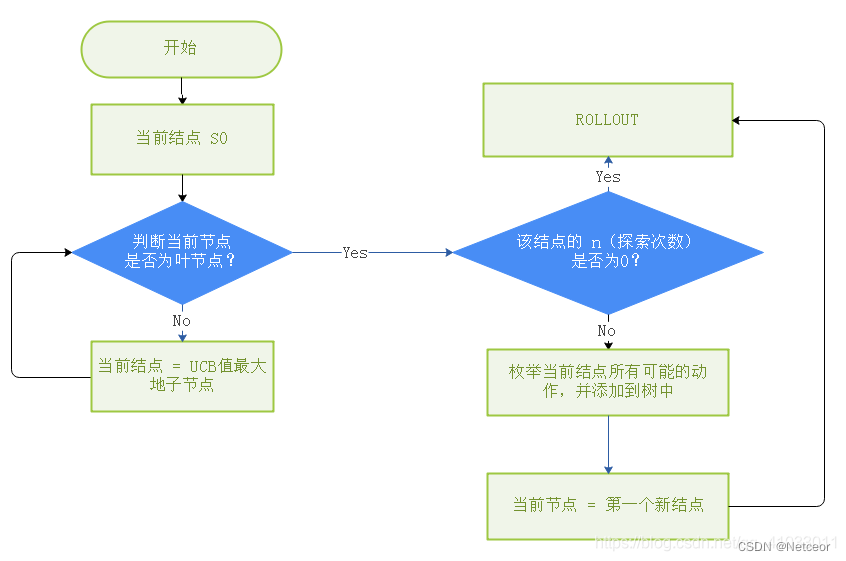
n代表当前节点被探索的次数。
则运行过程如下:
1、选择节点
- 当前节点是叶节点,则选择该节点
- 当前节点有孩子,孩子中UCB值最大的作为选择的节点
2、节点扩展 + 模拟
- 若选择的节点未模拟过(n=0),则进行模拟,得到结果后更新该节点 n=1 , value=结果数值。
- 若选择的节点模拟过(n≠0),则扩展节点。添加在该节点下所有可采取的动作,作为孩子
- 选择第一个孩子作为当前节点,进行模拟
def Rollout(S_i): # S_i = 当前状态While True: # S_i达到终止条件/状态(下棋中某方获胜或平局)if S_i a terimal state: # 返回结果valuereturn value(S_i) # 还未终止,则# 随机选择一个当前状态下的可用动作A_i = random(available_action(S_i)) # 在当前状态下采取动作,得到新的状态S_i = simulate(A_i, S_i)
3、反向传播
- 当孩子得到 Vc=v,nc+=1V_{c}=v,n_{c}+=1Vc=v,nc+=1,反向传播到父节点,父节点 Vp+=v,np+=1V_{p}+=v,n_{p}+=1Vp+=v,np+=1,直至传播到根节点。
三、实例
具体样例可参考博客蒙特卡洛树搜索(MCTS)详解、蒙特卡洛树搜索 MCTS 入门或b站视频AI如何下棋?直观了解蒙特卡洛树搜索MCTS!!!
相关文章:

蒙特卡洛树搜索(MTCS)
一、目标 一种启发式的搜索算法,在搜索空间巨大的场景下比较有效 算法完成后得到一棵树,这棵树可以实现:给定一个游戏状态,直接选择最佳的下一步 二、算法四阶段 1、选择(Selection) 父节点选择UCB值最…...
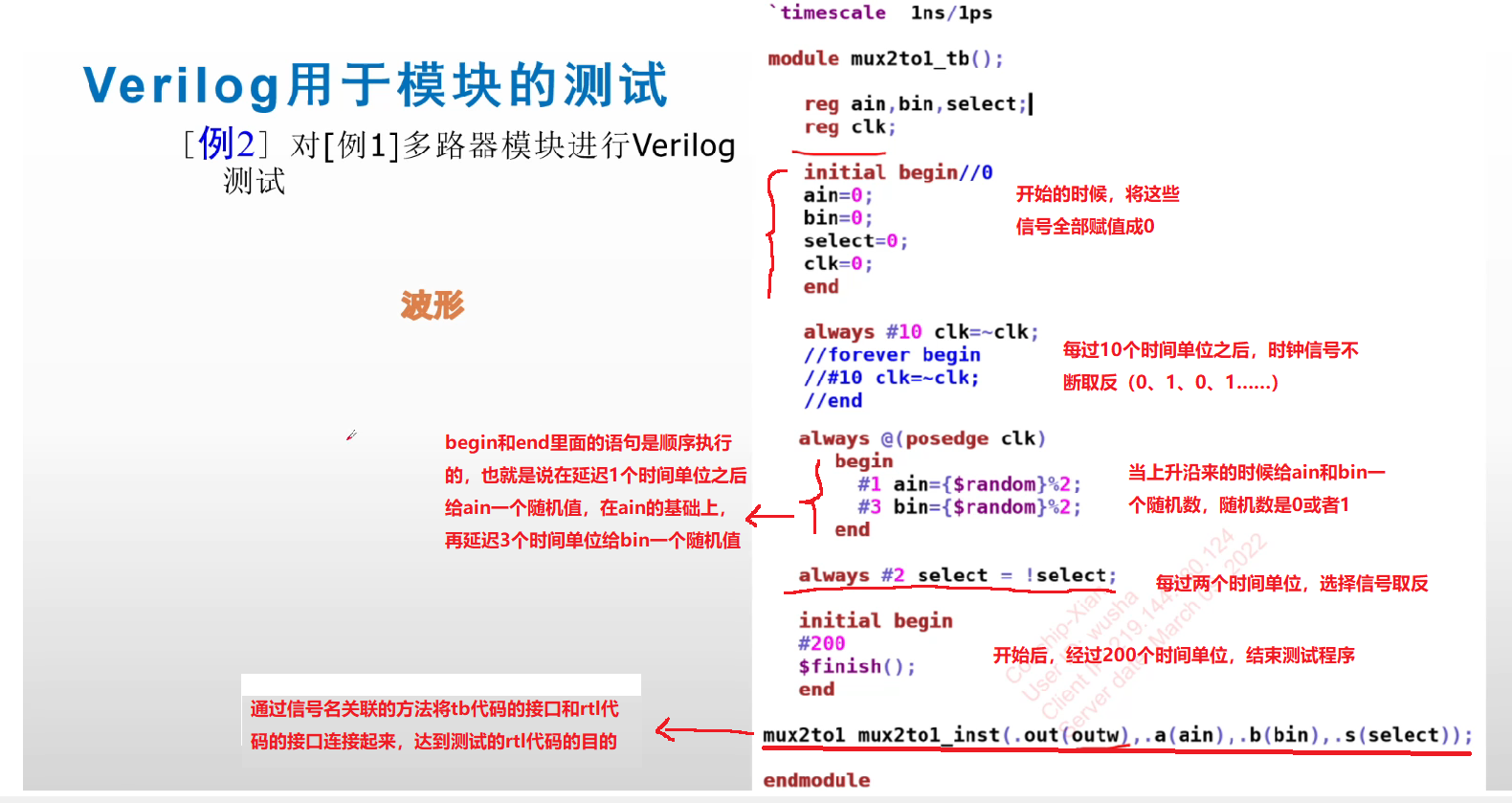
【Verilog】——Verilog简介
目录 1.简介 2.什么是HDL以及HDL的功能 3.Verilog和C语言的比较 4.Verilog的用途 5.数字系统的抽象层次 1.系统级 2.算法级 3.RTL级(寄存器变换级) 6.数字系统抽象层级 7.自顶向下的结构化设计方法 8.Verilog建模 9.Verilog概述 10.Verilog模块的基本…...
【Python从入门到进阶】10、流程控制语句-循环语句(for-while)
接上篇《9、流程控制语句-条件语句(if-else)》 上一篇我们学习了Python的控制流语句的概念,以及其中的条件语句(if/else),本篇我们来学习控制流语句中的循环语句(for/while)。 一、Python中的循环 Python的循环结构就是让程序“杀个回马枪”࿰…...
超全的命令(代码)执行漏洞无回显的姿势总结(附带详细代码和测试分析过程)
目录 漏洞代码 突破方式 重定向 dnslog外部通信 burpsuite burpcollaborator外部通信 日志监听 netcat监听 反弹shell的各种姿势 漏洞代码 <?php shell_exec($_GET[a]); ?>这里使用了无回显的shell执行函数shell_exec,给html目录的权限是777 突破方…...

STM32MP157-Linux音频应用编程-简易语音助手
文章目录前言STM32MP157简易语音助手alsa-lib简介:移植alsa-lib库:libcurl库简介:移植libcurl库:API调用修改asrmain.c文件修改token.c文件录音文件IO打开音频文件硬件控制sysfs文件系统数据解析和控制多线程主循环实现效果及注意…...

Python-OpenCV图像处理:学习图像算术运算,如加减法、图像混合、按位运算,以及如何实现它们
目录 目标 图像添加 图像混合算法 按位运算 目标 学习对图像的几种算术运算,如加法、减法、位运算等。了解这些功能:cv.add()、...
并发编程——ReentrantLock
如果有兴趣了解更多相关内容,欢迎来我的个人网站看看:耶瞳空间 一:基本介绍 从Java 5开始,引入了一个高级的处理并发的java.util.concurrent包,它提供了大量更高级的并发功能,能大大简化多线程程序的编写…...
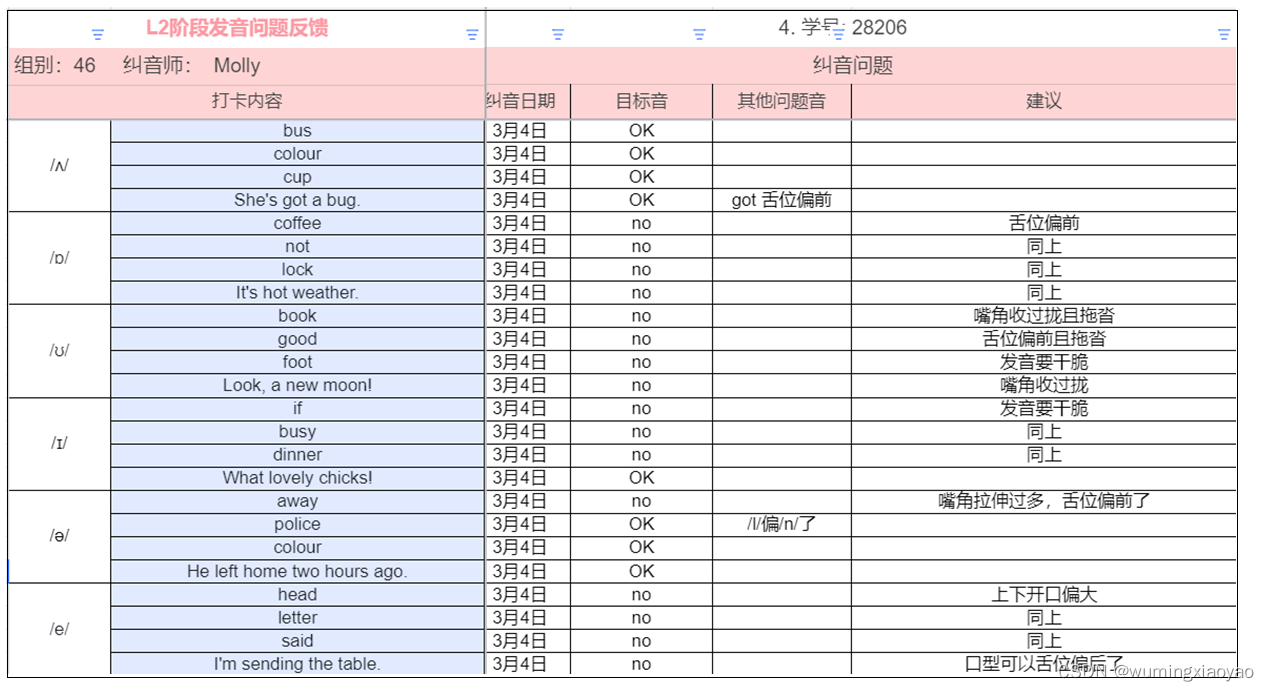
English Learning - L2 第 3 次小组纠音 [ʌ] [ɒ] [ʊ] [ɪ] [ə] [e] 2023.3.4 周六
English Learning - L2 第 3 次小组纠音 [ʌ] [ɒ] [ʊ] [ɪ] [ə] [e] 2023.3.4 周六共性问题小元音 [ʌ]小元音 [ɒ]小元音 [ʊ]小元音 [ɪ]小元音 [ə]小元音 [e]我的发音问题纠音过程共性问题 小元音 [ʌ] 口型容易偏大 解决办法:因为嘴角没有放松,…...
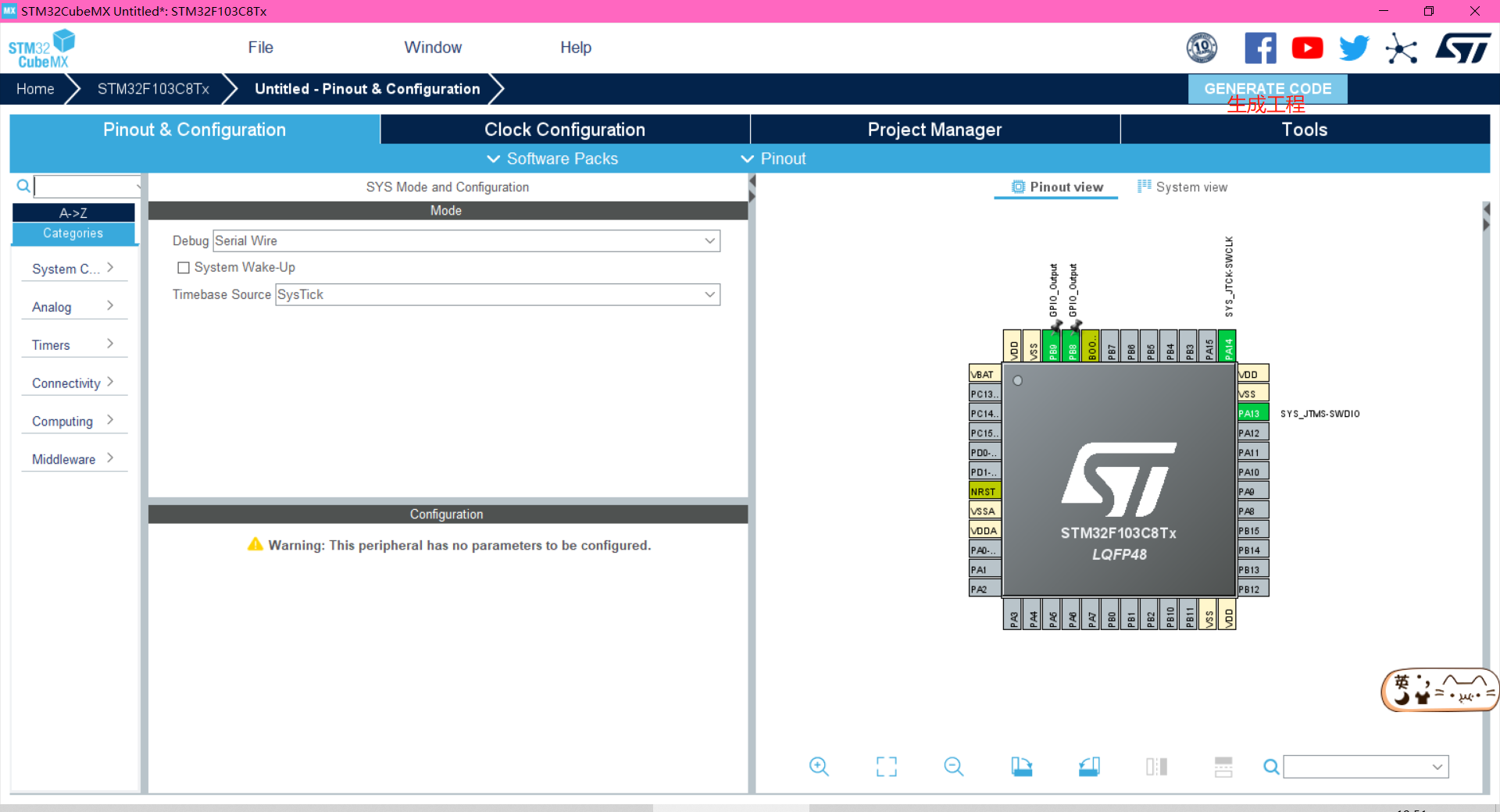
STM32之关门狗
看门狗介绍在由单片机构成的微型计算机系统中,由于单片机的工作常常会受到来自外界电磁场的干扰,造成程序的跑飞,而陷入死循环,程序的正常运行被打断,由单片机控制的系统无法继续工作,会造成整个系统的陷入…...

Apollo控制部分1-- ControlComponent组件介绍
Apollo控制部分1-- ControlComponent组件介绍摘要一、ControlComponent1、启动文件解析2、ControlComponent()组件函数解析1)ControlComponent::ControlComponent() 构造函数2)ControlComponent::Init() 初始化函数(执行一次)3&am…...

0626-0631韩顺平Java Buffered字节处理流 学习笔记
如何去构建字节流package com.hspedu.outputstream_;import java.io.*;/*** author abner* version 1.0*/ public class BufferedCopy02 {public static void main(String[] args) {String srcFilePath "D:\\Users\\Pictures\\Camera Roll\\Pierre-Auguste_Renoir,_Le_Mo…...
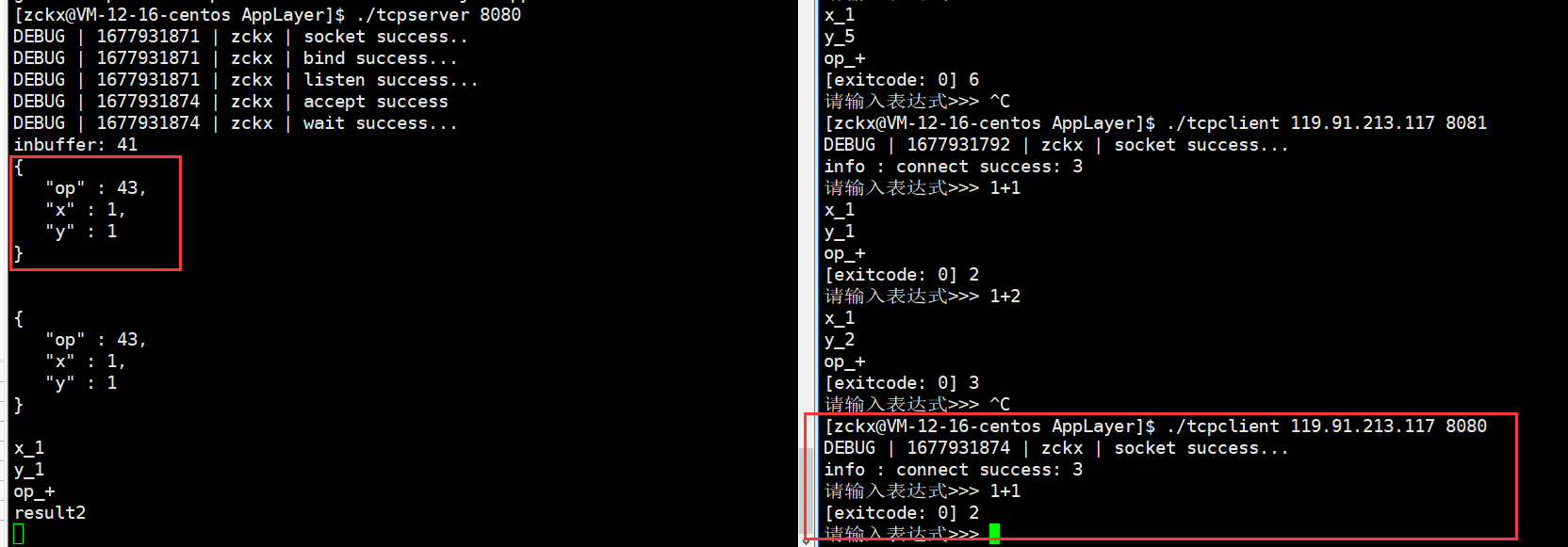
【网络】序列化和反序列化
🥁作者: 华丞臧. 📕专栏:【网络】 各位读者老爷如果觉得博主写的不错,请诸位多多支持(点赞收藏关注)。如果有错误的地方,欢迎在评论区指出。 推荐一款刷题网站 👉 LeetCode刷题网站 文章…...

【代码随想录训练营】【Day32】第八章|贪心算法|122.买卖股票的最佳时机II |55. 跳跃游戏|45.跳跃游戏II
买卖股票的最佳时机II 题目详细:LeetCode.122 买卖股票的最佳时机,怎么都能够想出来个思路,假如我们每天都能预知明天的股票是涨是降,那么贪心策略就是在涨之前买股票,在降的前一天卖掉,这就是买卖股票的…...

constexpr 和 常量表达式
👀👀常量表达式 常量表达式是指值不会改变并且在编译过程就能得到计算结果的表达式。 字面值属于常量表达式,用常量表达式初始化的const对象也是常量表达式。 那么是什么来就决定是不是常量表达式呢?一个对象是不是常量表达式主要…...
Vue响应式原理————Object.defineProperty()和proxy的用法分享
Vue框架一个比较核心的功能就是我们的数据是响应式的,这样我们在修改数据的时候,页面会自动帮我们更新,那么想要实现这个功能就要实现对一个数据的劫持,即在取值和设置值的同时我们能够检测到即数据劫持。vue2响应式的实现原理所依…...

CSDN 编程竞赛三十四期题解
竞赛总览 CSDN 编程竞赛三十四期:比赛详情 (csdn.net) 本期的题目和第三十一期竞赛的题目竟然高度重合,真不知道该写点什么了。 不过,上次那道测试数据有bug的题已经修复了,答题过程挺顺利的,没有遇到新的问题。 竞…...

C#教程06 运算符
文章目录 一、算术运算符加法运算符(+)减法运算符(-)乘法运算符(*)除法运算符(/)二、逻辑运算符与运算符(&&)或运算符(||)非运算符(!)三、比较运算符等于运算符(==)大于运算符(>)小于运算符(<)大于等于运算符(>=)小于等于运算符(<=…...
pytest单元测试)
软测入门(六)pytest单元测试
pytest pytest是python的一种单元测试框架,同自带的unit test测试框架类似,但pytest更简洁高效。 单元测试: 测试 函数、类、方法能不能正常运行测试的结果是否符合我们的预期结果 安装 pip install -U pytest基本使用 通过pytest包使用…...
)
经典分类模型回顾5—DenseNet实现图像分类(matlab)
DenseNet,全称为Densely Connected Convolutional Networks,中文名为密集连接卷积网络,是由李沐等人在2017年提出的一种深度神经网络架构。 DenseNet旨在解决深度神经网络中的梯度消失问题和参数数量过多的问题,通过构建密集连接…...
基于flask+bootstrap+echarts+mysql的鱼村小馆订餐后台管理系统
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
