神经网络基础——激活函数的选择、参数初始化
一、神经网络
1、神经网络
人工神经网络(Artificial Neural Network,即ANN)也简称为神经网络(NN)是一种模仿生物神经网络结构 和功能的计算模型。
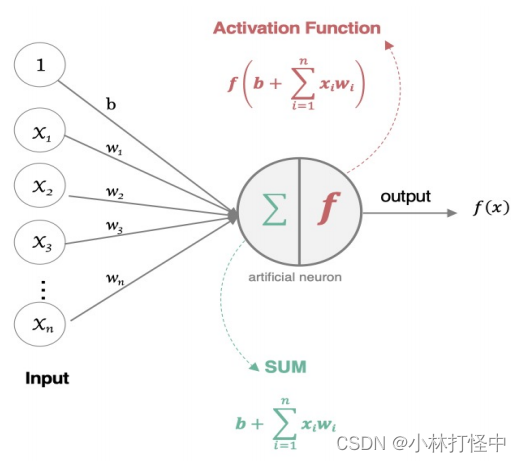
2、基本部分
输入层:输入 x
输出层:输出 y
隐藏层:输入与输出之间所有层
3、特点
同一层的神经元之间没有连接
第 N 层的每个神经元和第 N-1层 的所有神经元相连(full connected),即全连接神经网络
第 N-1层神经元的输出就是第 N 层神经元的输入
每个连接都有一个权重值(w系数和b系数)
二、激活函数
用于对每层的输出数据进行变换,进而为整个网络注入了非线性因素。此时, 神经网络就可以拟合各种曲线
1、sigmoid 激活函数
公式:

求导公式:

绘制函数图像:
import torch
import matplotlib.pyplot as plt# 函数图像
x = torch.linspace(-20,20,1000)
# 输入值x 通过 sigmoid函数 转换成 激活值y
y = torch.sigmoid(x)# 创建画布、坐标轴
plt.plot(x,y)
plt.grid()
plt.show()# 导数图像
x = torch.linspace(-20,20,1000,requires_grad=True)
# 自动微分
torch.sigmoid(x).sum().backward()plt.plot(x.detach(),x.grad)
plt.grid()
plt.show()
sigmoid 函数可以将任意的输入映射到 (0, 1) 之间,当输入的值大致在 <-6 或者 >6 时,意味着输入任何值 得到的激活值都是差不多的,这样会丢失部分信息。比如:输入 100 和输出 10000 经过 sigmoid 的激活值几乎都是等于 1 的,但是输入的数据之间相差 100 倍的信息就丢失了。
对于 sigmoid 函数而言,输入值在 [-6, 6] 之间输出值才会有明显差异,输入值在 [-3, 3] 之间才会有比较好的效果。
2、tanh 激活函数
公式:

求导公式:

函数图像:

3、ReLU 激活函数
公式: f (x) = max (0,x)
求导公式: f '(x) = 0 或 1
函数图像:
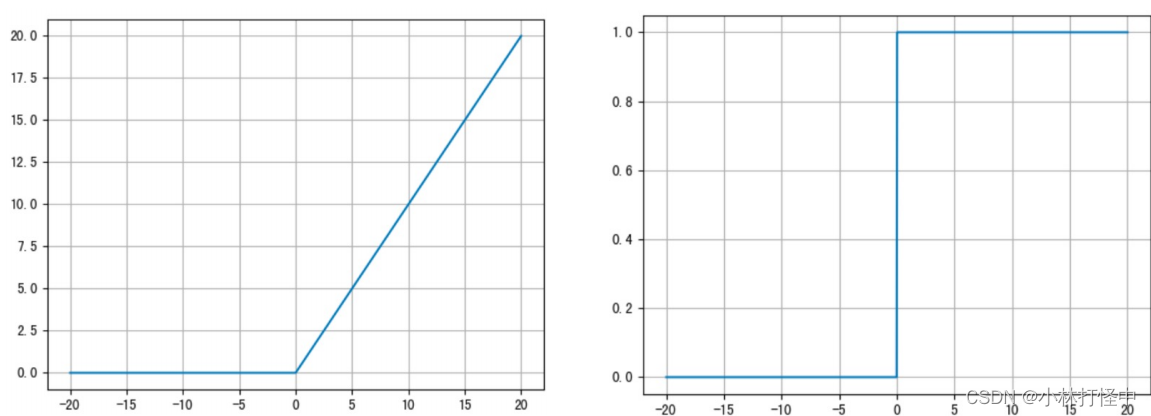
ReLU 激活函数将小于 0 的值映射为 0,而大于 0 的值则保持不变,它更加重视正信号,而忽略负信号,这种激活函数运算更为简单,能够提高模型的训练效率
当x<0时,ReLU导数为0,而当x>0时,则不存在饱和问题。所以,ReLU 能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。然而,随着训练的推进,部分输入会落入小于0区域,导致对应权重无法更新。这种现象被称为“神经元死亡”
ReLU是目前最常用的激活函数。与sigmoid相比,ReLU的优势是:采用sigmoid函数,计算量大(指数运算),反向传播求误差梯度时,计算量相对大,而采用Relu激活函数,整个过程的计算量节省很多。 sigmoid函数反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。 Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
4、SoftMax 激活函数
softmax用于多分类过程中,它是二分类函数sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来,公式如下:

Softmax 就是将网络输出的 logits 通过 softmax 函数,就映射成为(0,1)的值,而这些值的累和 为1(满足概率的性质),那么我们将它理解成概率,选取概率最大(也就是值对应最大的)节点,作为我们的预测目标类别。
scores = torch.tensor([0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75])
probabilities = torch.softmax(scores,dim=0)
print(probabilities)输出结果:
5、其他激活函数

6、选择方法
对于 隐藏层
1. 优先选择 ReLU激活函数
2. 如果ReLu效果不好,那么尝试其他激活,如Leaky ReLu等。
3. 如果使用了ReLU, 需要注意Dead ReLU问题, 避免出现大的梯度从而导致过多的神经元死亡。
4. 少用sigmoid激活函数,可以尝试使用tanh激活函数
对于 输出层
三、参数初始化
1、均匀分布 初始化
权重参数初始化从区间均匀随机取值,即在(,
)均匀分布中生成当前神经元的权重(d为每个神经元的输入数量)
import torch
import torch.nn.functional as F
import torch.nn as nn
# 均匀分布 随机初始化
def test01():linear = nn.Linear(5, 3)# 从 0 ~ 1 均匀分布产生参数nn.init.uniform_(linear.weight)print(linear.weight.data)2、正态分布 初始化
随机初始化从均值为0,标准差为1的高斯分布中取样,使用一些很小的值对参数W进行初始化
# 正态分布随机初始化
def test05():linear = nn.Linear(5, 3)nn.init.normal_(linear.weight, mean=0, std=1)print(linear.weight.data)3、全0 初始化
将神经网络中的所有权重参数初始化为 0
# 全0初始化
def test03():linear = nn.Linear(5, 3)nn.init.zeros_(linear.weight)print(linear.weight.data)4、全1 初始化
将神经网络中的所有权重参数初始化为 1
# 全1初始化
def test04():linear = nn.Linear(5, 3)nn.init.ones_(linear.weight)print(linear.weight.data)5、固定值初始化
将神经网络中的所有权重参数初始化为 某个固定值
# 固定初始化
def test02():linear = nn.Linear(5, 3)nn.init.constant_(linear.weight, 5)print(linear.weight.data)6、kaiming 初始化
正态化的HE初始化:均值为0,stddev(方差)=
均匀分布的HE初始化:从 [ -limit,limit ] 的均匀分布中抽取样本,limit =
input:输入神经元的个数
# kaiming 初始化
def test06():# kaiming 正态分布初始化linear = nn.Linear(5, 3)nn.init.kaiming_normal_(linear.weight)print(linear.weight.data)# kaiming 均匀分布初始化linear = nn.Linear(5, 3)nn.init.kaiming_uniform_(linear.weight)print(linear.weight.data)7、xavier 初始化
正态化的Xavier初始化:均值为0,stddev(方差)=
均匀分布的Xavier初始化:从 [ -limit,limit ] 的均匀分布中抽取样本,limit =
input:输入神经元的个数,output:输出神经元的个数
# xavier 初始化
def test07():# xavier 正态分布初始化linear = nn.Linear(5, 3)nn.init.xavier_normal_(linear.weight)print(linear.weight.data)# xavier 均匀分布初始化linear = nn.Linear(5, 3)nn.init.xavier_uniform_(linear.weight)print(linear.weight.data)四、网络搭建 和 参数计算
在pytorch中定义深度神经网络其实就是层堆叠的过程,继承自nn.Module,实现两个方法:
1. __init__方法中定义网络中的层结构,主要是全连接层,并进行初始化
2. forward方法,在实例化模型的时候,底层会自动调用该函数。该函数中可以定义学习率,
及数据传输方式。
构建如下图所示的神经网络模型:

编码设计如下:
1. 第1个隐藏层:权重采用标准化的 xavier初始化,激活函数 使用 sigmoid
2. 第2个隐藏层:权重采用标准化的 HE初始化,激活函数 用 relu
3. out 输出层:采用 softmax 做数据归一化
import torch
import torch.nn as nn
from torchsummary import summary # 计算模型参数,查看模型结构# 构建神经网络
class model(nn.Module):# 初始化属性值def __init__(self):# 调用父类的初始化属性值super(model,self).__init__()# 创建第一个隐藏层模型, 3个输入特征,3个输出特征self.layer1 = nn.Linear(3,3)# 初始化权重nn.init.xavier_normal_(self.layer1.weight)# 创建第二个隐藏层模型self.layer2 = nn.Linear(3,2)# 初始化权重nn.init.kaiming_normal_(self.layer2.weight)# 创建输出层模型self.out = nn.Linear(2,2)# 创建前向传播方法,自动执行forward()方法def forward(self,x):# 数据经过第一个线性层h1 = self.layer1(x)# 使用sigmoid激活函数h1 = torch.sigmoid(h1)# 数据经过第二个线性层h2 = self.layer2(h1)# 使用relu激活函数h2 = torch.relu(h2)# 数据经过输出层out = self.out(h2)# 使用softmax激活函数out = torch.softmax(out,dim=-1)return outif __name__ == '__main__':# 实例化model对象my_model = model()# 随机产生数据my_data = torch.randn(5,3)print('mydata shape',my_data.shape)# 数据经过 神经网络模型训练output = my_model(my_data)print('output shape',output.shape)# 计算模型参数# 计算每层每个神经元的w和b个数总和summary(my_model,input_size=(3,),batch_size=5)# 查看模型参数for name,parameter in my_model.named_parameters():print(name,parameter)输出结果:
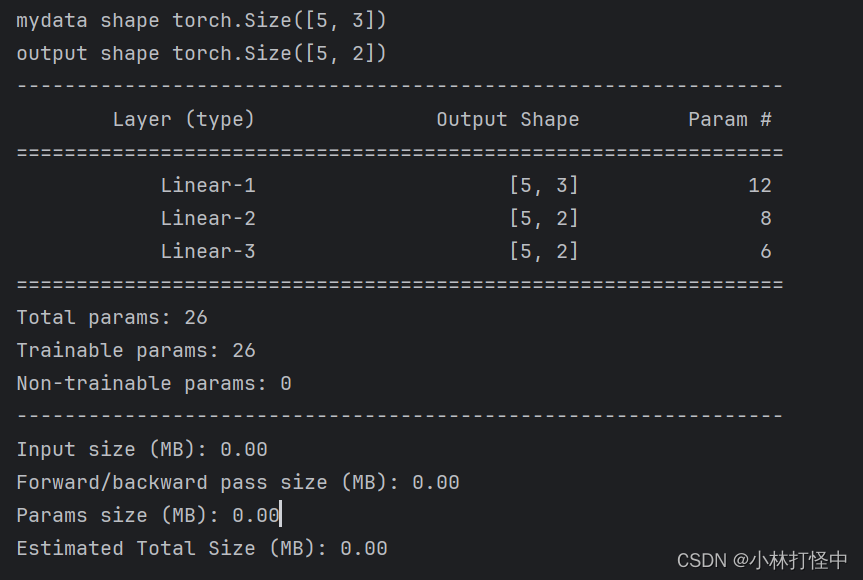
神经网络的优缺点:
优点
1. 精确度高、性能好、效果好
2. 拟合任意非线性的关系
3. 框架多,无需自己造轮子
缺点
1. 黑箱,可解释性差
2. 网络结构复杂,超参数多(超参数需要人工设置)
3. 需要大量的数据进行训练,训练时间长,对算力有较高要求
4. 小数据集容易过拟合
相关文章:

神经网络基础——激活函数的选择、参数初始化
一、神经网络 1、神经网络 人工神经网络(Artificial Neural Network,即ANN)也简称为神经网络(NN)是一种模仿生物神经网络结构 和功能的计算模型。 2、基本部分 输入层:输入 x 输出层:输出 y 隐…...
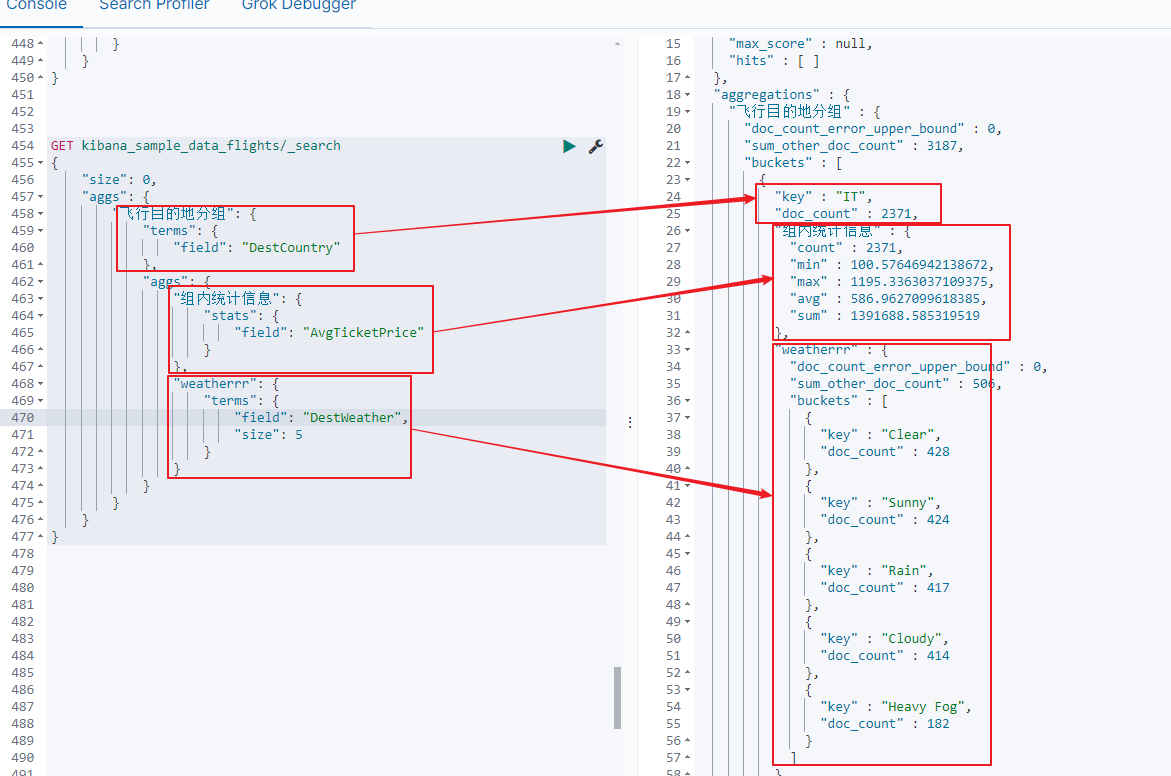
ElasticSearch之聚合aggs
写在前面 本文看下es的聚合相关内容。 1:什么是聚合 即,数据的统计分析。如sum,count,avg,min,max,分组等。 2:支持哪些聚合类型 2.1:bucket aggregation 对满足特…...

Android 系统定位和高德定位
文章目录 Android 系统定位和高德定位系统定位工具类封装LocationManager使用 高德定位封装高德地图使用 Android 系统定位和高德定位 系统定位 工具类 public class LocationUtils {public static final int REQUEST_LOCATION 0xa1;/*** 判断定位服务是否开启*/public sta…...
Day20_网络编程(软件结构,网络编程三要素,UDP网络编程,TCP网络编程)
文章目录 Day20 网络编程学习目标1 软件结构2 网络编程三要素2.1 IP地址和域名1、IP地址2、域名3、InetAddress类 2.2 端口号2.3 网络通信协议1、OSI参考模型和TCP/IP参考模型2、UDP协议3、TCP协议 2.4 Socket编程 3 UDP网络编程3.1 DatagramSocket和DatagramPacket1、Datagram…...
https://registry.npm.taobao.org淘宝npm镜像仓库地址更新
在工作中有遇见获取淘宝的npm镜像存在问题,图示如下的报错: 根据报错的内容是说 https://registry.npm.taobao.org地址访问失败了,然后通过排查发现淘宝的npm镜像仓库地址有更新了。需要使用最新的地址 旧的淘宝镜像仓库:https://…...

离散数学(一) 集合
属于关系 表示 枚举法; 叙述法; 文氏图法 基数 空集 全集 全集是相对唯一的 相等关系 有相同元素看作一个元素 包含关系 幂集 集合运算 并集 交集 补集 差集 对称差集 定理 可数集合与不可数集合 自然数集 等势 如果存在集合A到集合B的双射(又称一一…...

IOS不使用默认的mainStroryboard作为首个controller的方法
步骤1: 删除info.plist文件下的一条配置,如图 步骤2: 编辑AppDelegate.m,参考以下代码 interface AppDelegate () //property (strong, nonatomic) UIWindow * window; property(nonatomic,strong) UIWindow * win; property(…...
面试题 | 精选25项常问)
Qt(C++)面试题 | 精选25项常问
面试是每个求职者都必须经历的一关,而QT面试更是需要面试者有深厚的编程基础和丰富的实战经验。下面我们为大家整理了25道QT面试题,希望能够帮助大家在求职路上获得成功。 Qt 中常用的五大模块是哪些? Qt 中常用的五大模块包括: QtCore:提供了 Qt 的核心功能,例如基本的…...
个人博客系列-环境配置-gitee(2)
注册gitee账户 地址:https://gitee.com/ 此步骤省略 新建仓库 执行以下命令 即可 拉取代码 创建目录 mkdir myCode && cd myCode 登录gitee找到项目,点击克隆,拉取代码 连接远程仓库命令 git remote add origin 仓库地址http…...
DevOps 周期的 6 个 C
中型到大型软件开发项目涉及许多人员、多个团队、资源、工具和开发阶段。它们都需要以某种方式进行管理和简化,不仅可以获得所需的产品,而且还要确保将来在不断变化的环境下易于管理和维护。组织通常遵循许多项目管理模型和技术。DevOps 是其中之一&…...

九、计算机视觉-形态学基础概念
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、形态学的基本概念1.1 定义1.2 结构元素1.3 形态学操作 二、形态学的应用总结 前言 现在开始后面几课将介绍计算机视觉中的形态学理论和技术,包…...
杰发科技AC7801——SRAM 错误检测纠正
0.概述 7801暂时无错误注入,无法直接进中断看错误情况,具体效果后续看7840的带错误注入的测试情况。 1.简介 2.特性 3.功能 4.调试 可以看到在库文件里面有ecc_sram的库。 在官方GPIO代码里面写了点测试代码 成功打开2bit中断 因为没有错误注入&#x…...
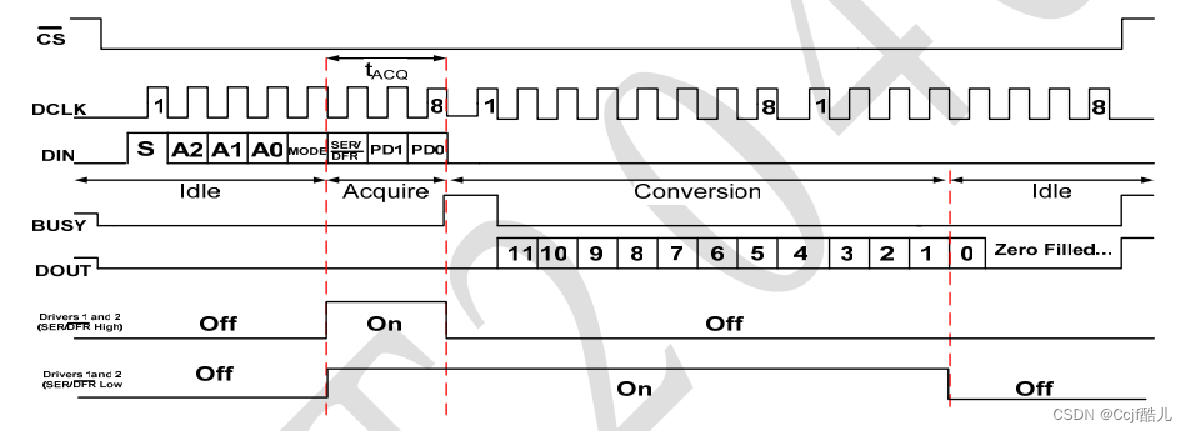
普中51单片机学习(AD转换)
AD转换 分辨率 ADC的分辨率是指使输出数字量变化一个相邻数码所需输入模拟电压的变化量。常用二进制的位数表示。例如12位ADC的分辨率就是12位,或者说分辨率为满刻度的1/(2^12)。 一个10V满刻度的12位ADC能分辨输入电压变化最小值是10V1/(2^12 )2.4mV。 量化误差 …...

YoloV8改进策略:主干网络改进|MogaNet——高效的多阶门控聚合网络
文章目录 摘要1、简介2、相关工作2.1、视觉Transformers2.2、ViT时代的卷积网络3、从多阶博弈论交互的角度看表示瓶颈4、方法论4.1、MogaNet概述4.2、多阶门控聚合4.3、通过通道聚合进行多阶特征重新分配4.4、实现细节5、实验5.1、ImageNet分类5.2、密集预测任务5.3、消融实验和…...

Sora:OpenAI引领创新浪潮的AI视频模型
Sora:OpenAI引领创新浪潮的AI视频模型 OpenAI作为人工智能领域的佼佼者,接下来,让我们一起深入了解Sora的技术特点、应用场景以及它对未来创作方式的潜在影响。 首先,让我们来探讨Sora的技术特点。Sora是一种基于深度学习的视频生…...

torch报错:[winerror 126] 找不到指定的模块torch_python.dll“ or one of its dependencies.
[winerror 126] 找不到指定的模块。 error loading "d:\miniconda\envs\action_env\lib\site-packages\torch\lib\torch_python.dll" or one of its dependencies. 在使用这个yolov5模块的时候发现了这个错误,错误原因是因为python版本和torch版本冲突。…...
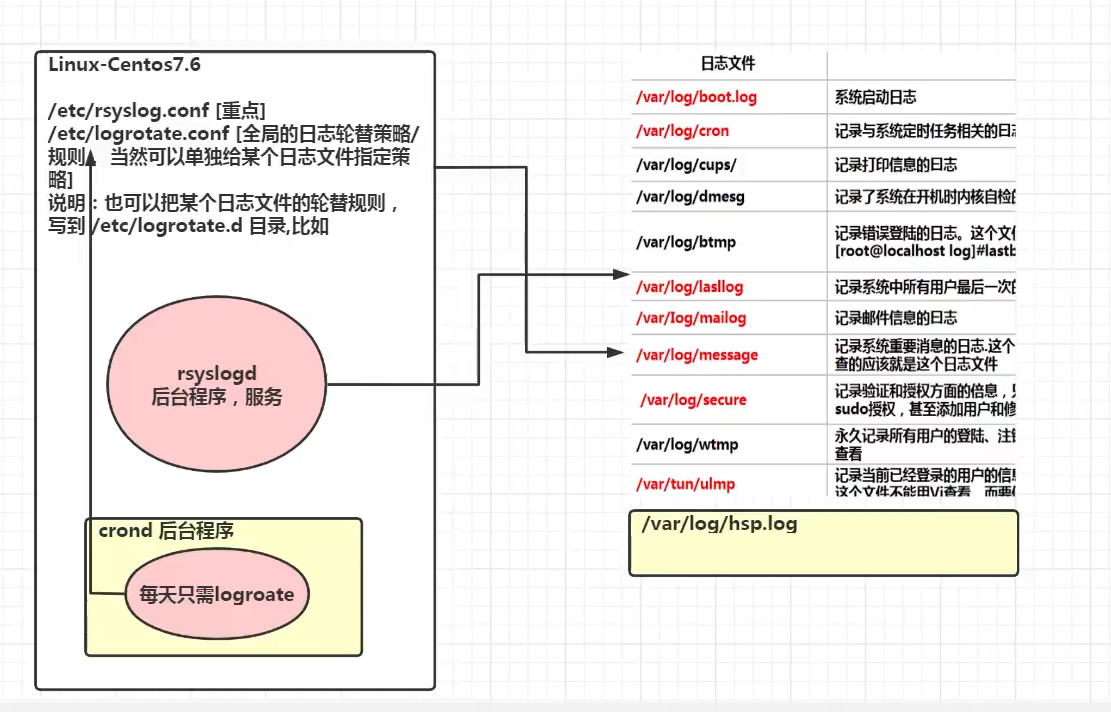
Linux日志轮替
文章目录 1. 基本介绍2. 日志轮替文件命名3. logrotate 配置文件4. 把自己的日志加入日志轮替5. 日志轮替机制原理6. 查看内存日志 1. 基本介绍 日志轮替就是把旧的日志文件移动并改名,同时建立新的空日志文件,当旧日志文件超出保存的范围之后ÿ…...

Docker Container(容器)
"在哪里走散,你都会找到我~" Docker 容器 什么是容器? 通俗来讲,容器是镜像运行的实体。我们对于镜像的认知是,“存储在磁盘上的只读文件”。当我们启动一个容器的本质,就是启动一个进程,即容器…...

week04day03(爬虫 beautifulsoup4、)
一. 使用bs4解析网页 下载bs4 - pip install beautifulsoup4 使用的时候 import bs4专门用于解析网页的第三方库 在使用bs4的时候往往会依赖另一个库lxml pip install lxml 网页代码 <!DOCTYPE html> <html><head><meta charset"utf-8"><…...
04 动力云客之登录后获取用户信息+JWT存进Redis+Filter验证Token + token续期
1. 登录后获取用户信息 非常好实现. 只要新建一个controller, 并调用SS提供的Authentication对象即可 package com.sunsplanter.controller;RestController public class UserController {GetMapping(value "api/login/info")public R loginInfo(Authentication a…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
