(done) Positive Semidefinite Matrices 什么是半正定矩阵?如何证明一个矩阵是半正定矩阵? 可以使用特征值
参考视频:https://www.bilibili.com/video/BV1Vg41197ew/?vd_source=7a1a0bc74158c6993c7355c5490fc600
参考资料(半正定矩阵的定义):https://baike.baidu.com/item/%E5%8D%8A%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/2152711?fr=ge_ala
看看半正定矩阵的定义:

正定矩阵是 > 0,半正定矩阵是 >= 0
根据定义来看,半正定矩阵也有 “实对称矩阵” 的前提条件
或许我们可以考虑 半正定矩阵性质 和 “特征值特性” 之间的关系,证明方法可以参考之前 “正定矩阵的特征值特性” 的证明方法
首先大胆假设:半正定矩阵 <=> 特征值都 >= 0
那么,设 半正定矩阵 A
先试着证明 半正定矩阵 => 特征值都 >= 0:
- 对于非零任意特征向量 x, x’ A x = x’ (lamda) x = (lamda) x’x >= 0
- 由于特征向量 x 是非零向量,所以 (lamda) >= 0 (可以为 0)
- 这个方向证明完毕
再试着证明 特征值都 >= 0 ===> 半正定矩阵
- 对于任意一个非零向量 x,x’ A x = x’ Q’ (hat) Q x (这是正交相似对角化) (其中 (hat) 是对角矩阵,由于 A 的特征值组成)
- x’ A x = x’ Q’ (hat) Q x = (Qx)’ (hat) (Qx) (其中 (hat) 是对角矩阵,由 A 的特征值组成)
- 由于 x 是非零向量,Q是正交矩阵,所以 (Qx) 是非零向量
- 其中 (hat) 是对角矩阵,对角线上元素由 A 的特征值 (lamda) 组成,(lamda) >= 0,因此 (hat) 也是半正定矩阵
- 于是, (Qx)’ (hat) (Qx) >= 0
- 所以 x’ A x >= 0
- 因此,矩阵 A 是半正定矩阵
- 证明完毕
up主给的笔记有误,勘误如下:
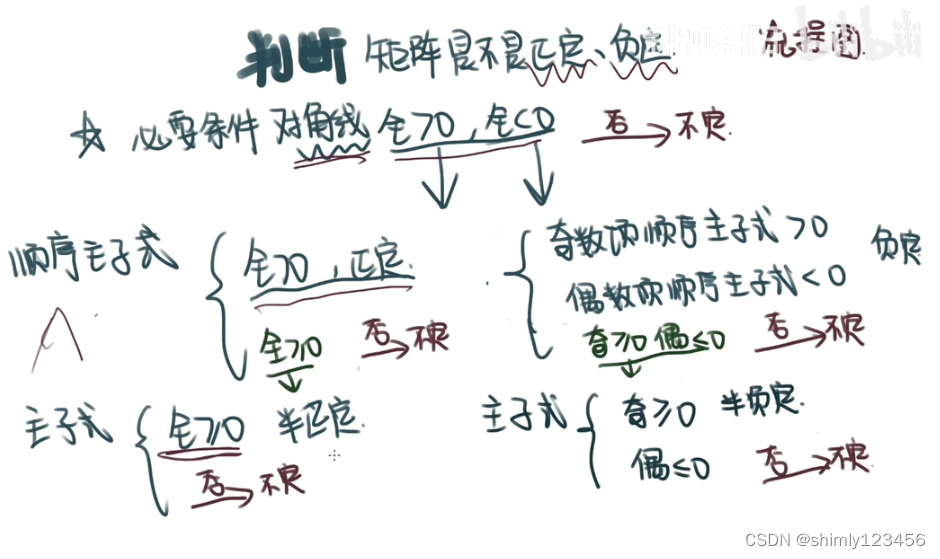
如下图是判断正定负定、半正定半负定的方法
不对!不对! up 主错了!!!
对角线上的元素有 0 元素,依然可以是半正定矩阵
我们在后面看个例子
栗子在这里:

相关文章:

(done) Positive Semidefinite Matrices 什么是半正定矩阵?如何证明一个矩阵是半正定矩阵? 可以使用特征值
参考视频:https://www.bilibili.com/video/BV1Vg41197ew/?vd_source7a1a0bc74158c6993c7355c5490fc600 参考资料(半正定矩阵的定义):https://baike.baidu.com/item/%E5%8D%8A%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/2152711?frge_ala 看看半正定矩阵的…...

七、矩阵的初等变换
目录 -1. 介绍 0、增广矩阵: 1、初等变换的性质: 编辑2、矩阵初等变换的分类: 2.1 普通的行阶梯矩阵: 2.2 、行最简形矩阵: 2.3、标准形矩阵: 3、初等变换的定理: 4、初等变换的应用&…...

CSS background-size
background-size 菜鸟教程 CSS3 background-size 属性 MDN Web 开发技术>CSS:层叠样式表>background-size CSS的background 背景图片自动适应元素大小,实现img的默认效果 background-size:100% 100%; 在CSS中,background-size属性用…...

【机器学习】特征工程之特征选择
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...

Java中PDF文件传输有哪些方法?
专栏集锦,大佬们可以收藏以备不时之需: Spring Cloud 专栏:http://t.csdnimg.cn/WDmJ9 Python 专栏:http://t.csdnimg.cn/hMwPR Redis 专栏:http://t.csdnimg.cn/Qq0Xc TensorFlow 专栏:http://t.csdni…...
前后端分离Vue+ElementUI+nodejs蛋糕甜品商城购物网站95m4l
本文主要介绍了一种基于windows平台实现的蛋糕购物商城网站。该系统为用户找到蛋糕购物商城网站提供了更安全、更高效、更便捷的途径。本系统有二个角色:管理员和用户,要求具备以下功能: (1)用户可以修改个人信息&…...

Pytorch 复习总结 3
Pytorch 复习总结,仅供笔者使用,参考教材: 《动手学深度学习》Stanford University: Practical Machine Learning 本文主要内容为:Pytorch 多层感知机。 本文先介绍了多层感知机的用法,再就训练过程中经常出现的过拟…...

2024年危险化学品经营单位主要负责人证考试题库及危险化学品经营单位主要负责人试题解析
题库来源:安全生产模拟考试一点通公众号小程序 2024年危险化学品经营单位主要负责人证考试题库及危险化学品经营单位主要负责人试题解析是安全生产模拟考试一点通结合(安监局)特种作业人员操作证考试大纲和(质检局)特…...

go使用trpc案例
1.go下载trpc go install trpc.group/trpc-go/trpc-cmdline/trpclatest 有报错的话尝试配置一些代理(选一个) go env -w GOPROXYhttps://goproxy.cn,direct go env -w GOPROXYhttps://goproxy.io,direct go env -w GOPROXYhttps://goproxy.baidu.com/…...
nodejs+vue+ElementUi废品废弃资源回收系统
系统主要是以后台管理员管理为主。管理员需要先登录系统然后才可以使用本系统,管理员可以对系统用户管理、用户信息管理、回收站点管理、站点分类管理、站点分类管理、留言板管理、系统管理进行添加、查询、修改、删除,以保障废弃资源回收系统系统的正常…...

【Java程序设计】【C00277】基于Springboot的招生管理系统(有论文)
基于Springboot的招生管理系统(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的招生管理系统 本系统分为系统功能模块、管理员功能模块以及学生功能模块。 系统功能模块:在系统首页可以查看首页、专业…...

汇编语言与接口技术实践——秒表
1. 设计要求 基于 51 开发板,利用键盘作为按键输入,将数码管作为显示输出,实现电子秒表。 功能要求: (1)计时精度达到百分之一秒; (2)能按键记录下5次时间并通过按键回看 (3)设置时间,实现倒计时,时间到,数码管闪烁 10 次,并激发蜂鸣器,可通过按键解除。 2. 设计思…...

【数据结构与算法】(19)高级数据结构与算法设计之 图 拓扑排序 最短路径 最小生成树 不相交集合(并查集合)代码示例
目录 6) 拓扑排序KahnDFS 7) 最短路径DijkstraBellman-FordFloyd-Warshall 8) 最小生成树PrimKruskal 9) 不相交集合(并查集合)基础路径压缩Union By Size 图-相关题目 6) 拓扑排序 #mermaid-svg-MQhLsXiMwnlUL3q4 {font-family:"trebuchet ms"…...

OSCP靶场--Nickel
OSCP靶场–Nickel 考点(1.POST方法请求信息 2.ftp,ssh密码复用 3.pdf文件密码爆破) 1.nmap扫描 ┌──(root㉿kali)-[~/Desktop] └─# nmap 192.168.237.99 -sV -sC -p- --min-rate 5000 Starting Nmap 7.92 ( https://nmap.org ) at 2024-02-22 04:06 EST Nm…...

新建工程——库函数版
新建工程——库函数版 s t e p I : 新建工程文件夹 \bf{stepI:新建工程文件夹} stepI:新建工程文件夹 s t e p I I : K e i l 5 新建工程 \bf{stepII:Keil5新建工程} stepII:Keil5新建工程 s t e p I I I : 最终得到工程文件 \bf{stepIII:最终得到工程文件} stepIII:最终得到工…...
java 数据结构栈和队列
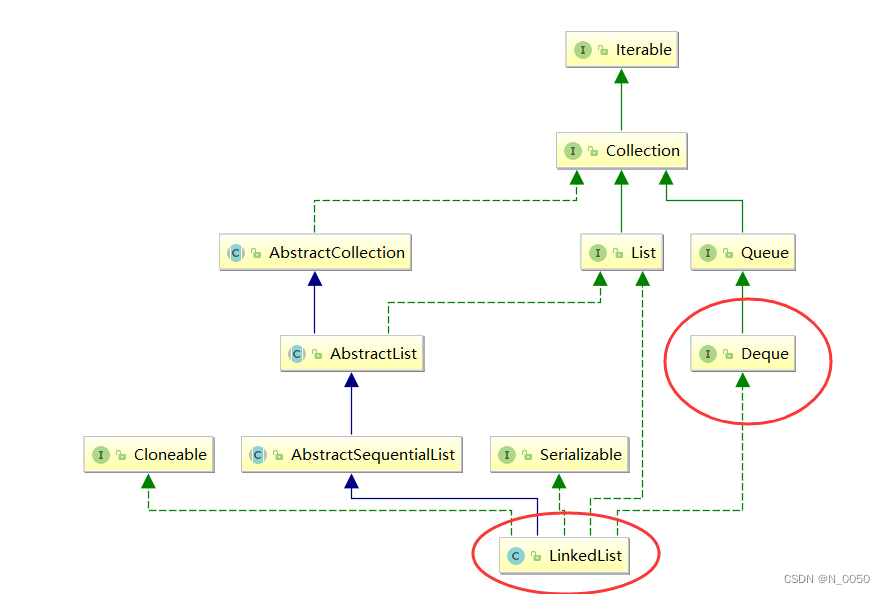
目录 栈(Stack) 栈的使用 栈的模拟实现 栈的应用场景 队列(Queue) 队列的使用 队列模拟实现 循环队列 双端队列 用队列实现栈 用栈实现队列 栈(Stack) 什么是栈? 栈 :一种特殊的线性表,其 只允许在固定的一端进行插入和删除元素操…...

#LLM入门|Prompt#1.8_聊天机器人_Chatbot
聊天机器人设计 以会话形式进行交互,接受一系列消息作为输入,并返回模型生成的消息作为输出。原本设计用于简便多轮对话,但同样适用于单轮任务。 设计思路 个性化特性:通过定制模型的训练数据和参数,使机器人拥有特…...
LeetCode 2476.二叉搜索树最近节点查询:中序遍历 + 二分查找
【LetMeFly】2476.二叉搜索树最近节点查询:中序遍历 二分查找 力扣题目链接:https://leetcode.cn/problems/closest-nodes-queries-in-a-binary-search-tree/ 给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 qu…...

选座位 - 华为OD统一考试(C卷)
OD统一考试(C卷) 分值: 200分 题解: Java / Python / C 题目描述 疫情期间,需要大家保证一定的社交距离,公司组织开交流会议,座位有一排共N个座位,编号分别为[0…N-1],要…...
【微服务】mybatis typehandler使用详解
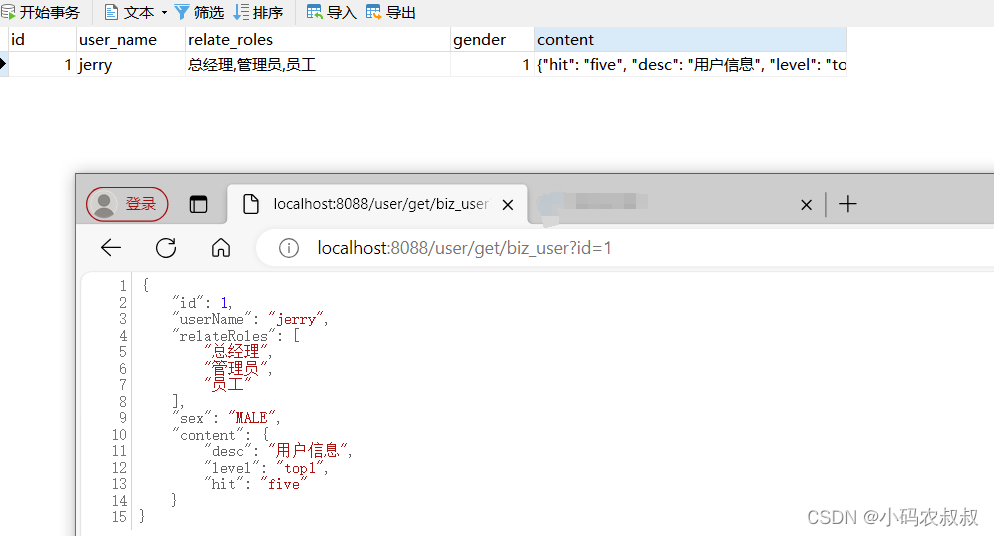
目录 一、前言 二、TypeHandler简介 2.1 什么是TypeHandler 2.1.1 TypeHandler特点 2.2 TypeHandler原理 2.3 mybatis自带的TypeHandler 三、环境准备 3.1 准备一张数据表 3.2 搭建一个springboot工程 3.2.1 基础依赖如下 3.2.2 核心配置文件 3.2.3 测试接口 四、T…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
