牛客周赛 Round 34 解题报告 | 珂学家 | 构造思维 + 置换环
前言
整体评价
好绝望的牛客周赛,彻底暴露了CF菜菜的本质,F题没思路,G题用置换环骗了50%, 这大概是唯一的亮点了。
A. 小红的字符串生成
思路: 枚举
a,b两字符在相等情况下比较特殊
a, b = input().split()
if a == b:print (2)print (a)print (a + a)
else:print (4)print (a)print (b)print (a + b)print (b + a)
B. 小红的非排列构造
思路: 脑筋急转弯
如果合法,就是0
如果不合法,就把第1项改为n+1(排列外的数)
n = int(input())
arr = list(map(int, input().split()))si = set()
for v in arr:if 1 <= v <= n:si.add(v)
if len(si) != n:print (0)
else:print (1)print (1, n + 1)
C. 小红的数字拆解
思路: 贪心
从高位到低位贪心即可
s = input()arr = []i = 0
while i < len(s):j = iwhile j < len(s):p = ord(s[j]) - ord('0')if p % 2 == 0:breakj += 1arr.append(s[i:j+1])i = j + 1arr.sort(key=lambda x: (len(x), x))print (*arr, sep='\n')
D. 小红的陡峭值
思路: 构造
这题是限制性很强的题, 绝对差值总和为1
对于不满足条件数组,可以立马返回 -1.
难点在于
如何构造合法数组 如何构造合法数组 如何构造合法数组
假定0元素(左右两侧都存在非0值),和左侧元素保持一致(反证法使得该假设一定成立)
那就剩下一侧有非0值的0值,如何讨论呢?
- 如果绝对差值总和为1
- 那就和左侧/右侧的那个非0值,保持一致
- 如果绝对差值总和为0
- 那就选一边构造一个比左侧/右侧刚好大1的数
n = int(input())
arr = list(map(int, input().split()))if arr == [0 for _ in range(n)]:if len(arr) == 1:print (-1)else:print (*([1] + [2] * (n - 1)), sep=' ')
else:# 计算当前的差值综合brr = [v for v in arr if v > 0]diff = 0for i in range(len(brr) - 1):diff += abs(brr[i] - brr[i+1])if diff > 1:print (-1)else:first, last = -1, -1for i in range(n):if arr[i] != 0:if first == -1:first = ilast = i # 填充中间的值pre = arr[first]for i in range(first + 1, last):if arr[i] == 0:arr[i] = preelse:pre = arr[i]# 填充两端的值if diff == 1:# 需要两端保持绝对值差值为0for i in range(first):arr[i] = arr[first]for i in range(last + 1, n):arr[i] = arr[last]print (*arr, sep=' ')else:# 需要两端构建出一个绝对值差值1if first > 0:for i in range(first):arr[i] = arr[first] + 1for i in range(last + 1, n):arr[i] = arr[last]print (*arr, sep=' ')elif last + 1 < n:for i in range(last + 1, n):arr[i] = arr[last] + 1print (*arr, sep=' ')else:print (-1)
E. 小红的树形 dp
思路: BFS + 验证
属于诈骗题,因为题目一直再诱导你往树形DP上去靠
其实从bfs出发,进行交叉染色
然后对边上两点进行验证,如果存在同色,即不合法
n = int(input())
s = input()
ss = list(s)g = [[] for _ in range(n)]for _ in range(n - 1):u, v = list(map(int, input().split()))u -= 1v -= 1g[u].append(v)g[v].append(u)from collections import dequedeq = deque()
for i in range(n):if ss[i] != '?':deq.append((i, ss[i]))# 需要补充这种特殊情况
if len(deq) == 0:ss[0] = 'd'deq.append((0, ss[0]))# BFS流程
while len(deq) > 0:idx, ch = deq.popleft()for v in g[idx]:if ss[v] == '?':ss[v] = 'd' if ch == 'p' else 'p'deq.append((v, ss[v]))# 验证逻辑
ok = True
for i in range(n):ch = ss[i]if ch == '?':ok = Falsebreakfor v in g[i]:if ch == 'd' and ss[v] != 'p':ok = Falsebreakif ch == 'p' and ss[v] != 'd':ok = Falsebreakif not ok:print (-1)
else:print (''.join(ss))
F. 小红的矩阵构造
思路: 异或特性
贴一下皮神的代码
代码即是说服力
n, m, x = map(int, input().split())res = [[0] * m for _ in range(n)]if x % 4 == 0:res[0][0] = res[0][1] = res[1][0] = res[1][1] = x // 4for ls in res:print(*ls)
elif x == 2:print(-1)
else:res[2][0] = res[2][1] = 1res[1][0] = res[1][2] = 1res[0][1] = res[0][2] = 1for i in [0, -1]:for j in [0, -1]:res[i][j] += (x - 6) // 4for ls in res:print(*ls)
G. 小红的元素交换
思路: 置换环 + 找规律
假如这题没有交换颜色的限制,那这题就是裸的置换环
但是实际上,这题的核心框架依旧是
置换环 置换环 置换环
具体情况需要分类讨论
-
同一置换环(a个元素)中存在两种颜色, 则交换一定为a-1
-
同一置换环(a个元素)中只存在1种颜色, 则需要借助外部的非同色,这样为a-1+2=a+1
但是这样做,只能对大致50%+
为啥呢?
因为对于纯色R的置换环,和纯色W的置换环,其实可以互相借调,因此这一组合,可以减少2次不必要的交换。
因此在原先的基础上,需要优化减掉
m i n ( 纯色 R 的群数,纯色 W 的群数 ) ∗ 2 min(纯色R的群数,纯色W的群数) * 2 min(纯色R的群数,纯色W的群数)∗2
n = int(input())
arr = list(map(int, input().split()))
s = input()from collections import Counterif [i + 1 for i in range(n)] != arr and len(Counter(s)) == 1:print(-1)
else:res = 0white, red = 0, 0for i in range(n):if arr[i] == i + 1:continueelse:# 置换环核心逻辑state = 0tmp = 0while arr[i] != i + 1:p1, p2 = i, arr[i] - 1arr[p1], arr[p2] = arr[p2], arr[p1]tmp += 1state |= 2 if s[p1] == 'R' else 1state |= 2 if s[p2] == 'R' else 1# 分类讨论置换环的纯色情况if state == 3:res += tmpelse:# 纯色,需要借调外部力量res += tmp + 2if state == 1:white += 1else:red += 1print(res - min(white, red) * 2)
写在最后

相关文章:

牛客周赛 Round 34 解题报告 | 珂学家 | 构造思维 + 置换环
前言 整体评价 好绝望的牛客周赛,彻底暴露了CF菜菜的本质,F题没思路,G题用置换环骗了50%, 这大概是唯一的亮点了。 A. 小红的字符串生成 思路: 枚举 a,b两字符在相等情况下比较特殊 a, b input().split() if a b:print (2)print (a)pri…...

LeetCode13 罗马数字转整数
题目 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例如&…...
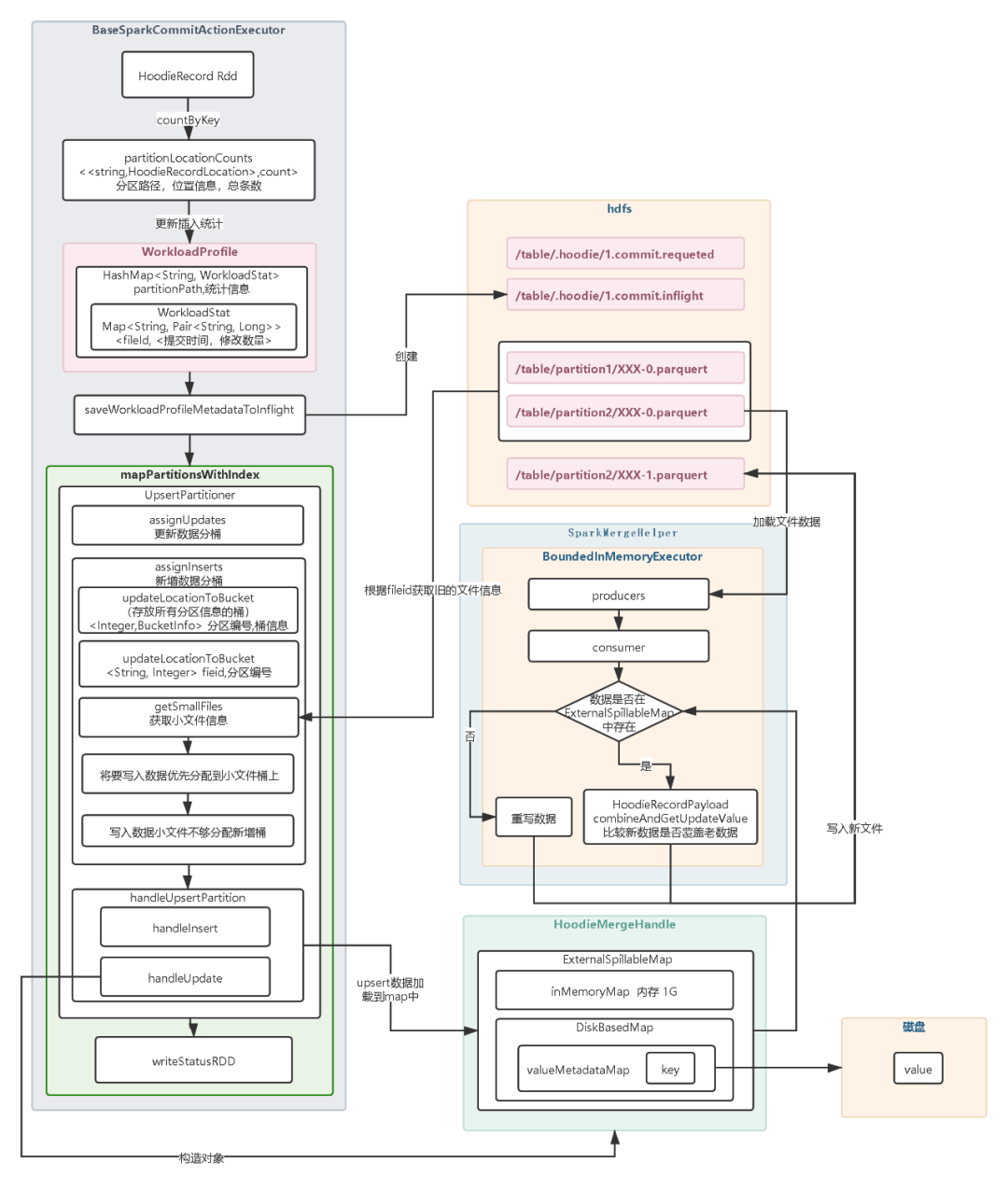
【Hudi】Upsert原理
17张图带你彻底理解Hudi Upsert原理 1.开始提交:判断上次任务是否失败,如果失败会触发回滚操作。然后会根据当前时间生成一个事务开始的请求标识元数据。2.构造HoodieRecord Rdd对象:Hudi 会根据元数据信息构造HoodieRecord Rdd 对象…...

信息系统服务:演绎数字时代的征程
信息系统服务作为数字化时代的基石,已经在人类社会的各个领域发挥着重要作用。本文将从信息系统服务的起源、发展和演化过程,通过生动的例子和准确客观的历史事实,探讨信息系统服务对人类社会的影响与变革。 1. 起源:信息处理的初…...

rust连接postgresql数据库
引入crate: postgres "0.19.7" use postgres::{Client, NoTls, error::Error};fn main() -> Result<(), Error> {let mut client Client::connect("hostlocalhost port5432 dbnamexxxxdb userpostgres passwordxxxxxx", NoTls).un…...

[面试] 什么是死锁? 如何解决死锁?
什么是死锁 死锁,简单来说就是两个或者多个的线程在执行的过程中,争夺同一个共享资源造成的相互等待的现象。如果没有外部干预线程会一直阻塞下去. 导致死锁的原因 互斥条件,共享资源 X 和 Y 只能被一个线程占用; 请求和保持条件…...
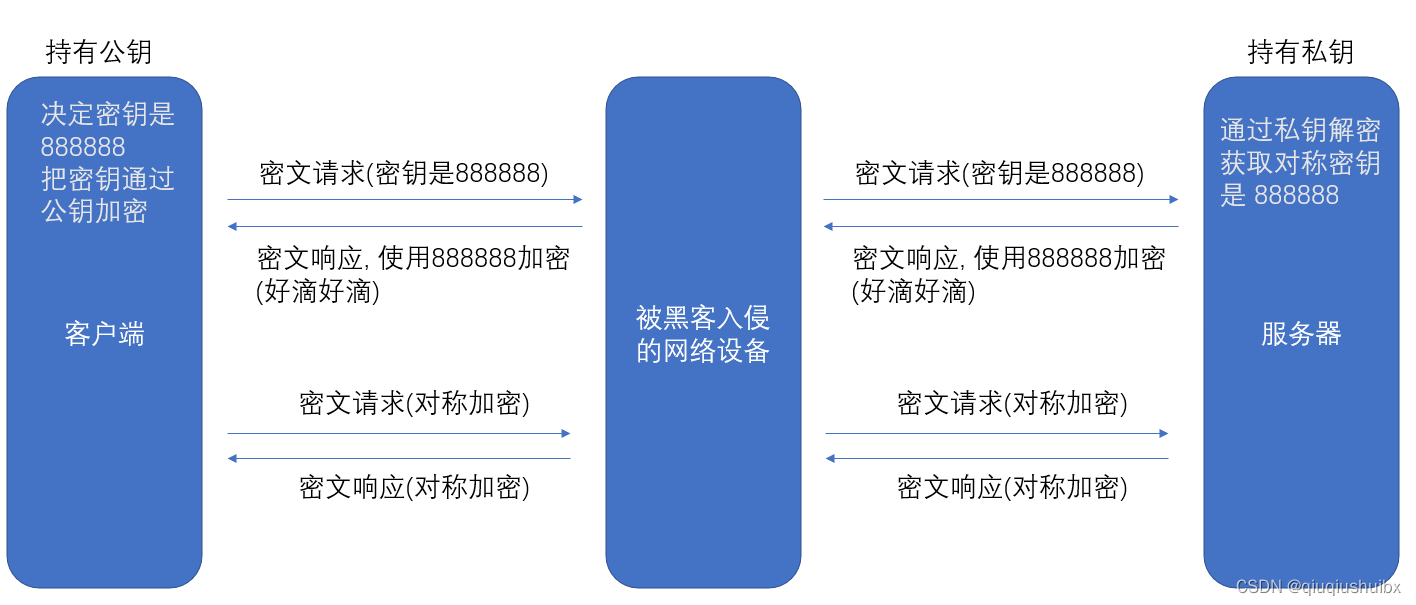
网络原理 HTTP _ HTTPS
回顾 我们前面介绍了HTTP协议的请求和响应的基本结构 请求报文是由首行请求头空行正文来组成的 响应报文是由首行形影头空行响应正文组成的 我们也介绍了一定的请求头之中的键值对的属性 Host,Content-type,Content-length,User-agent,Referer,Cookie HTTP协议中的状态码 我们先…...

软件实际应用实例,茶楼收银软件管理系统操作流程,茶室计时计费会员管理系统软件试用版教程
软件实际应用实例,茶楼收银软件管理系统操作流程,茶室计时计费会员管理系统软件试用版教程 一、前言 以下软件以 佳易王茶社计时计费管理系统软件V17.9为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 1、计时计费&…...
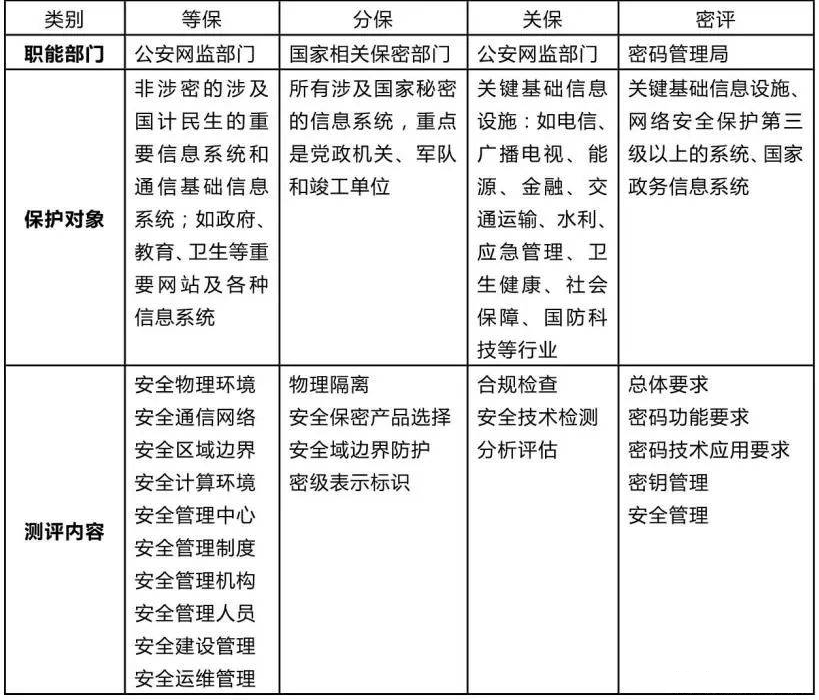
网络安全“三保一评”深度解析
“没有网络安全就没有国家安全”。近几年,我国法律法规陆续发布实施,为承载我国国计民生的重要网络信息系统的安全提供了法律保障,正在实施的“3保1评”为我国重要网络信息系统的安全构筑了四道防线。 什么是“3保1评”? 等保、分…...
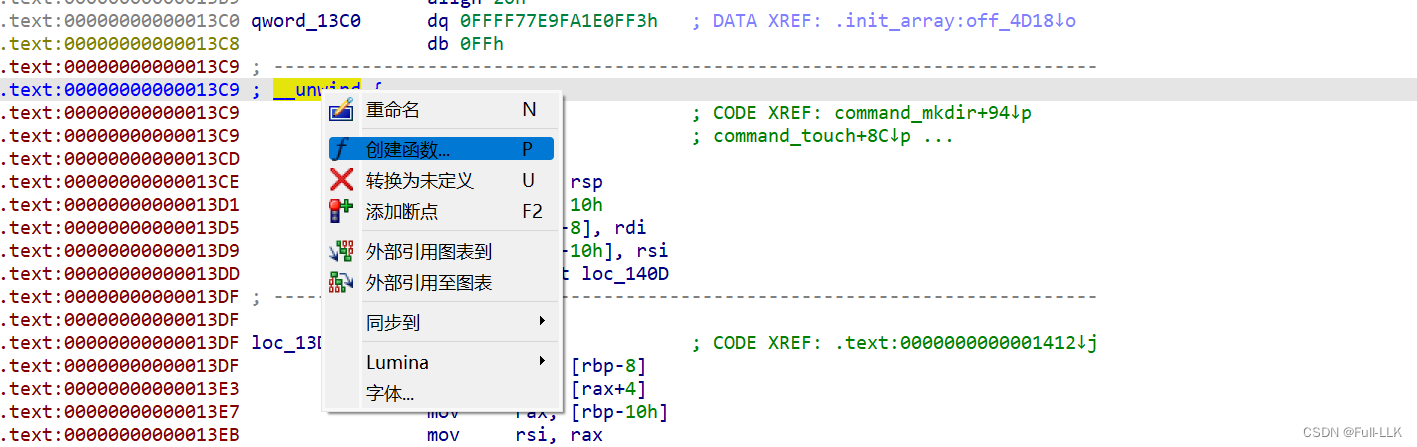
IDA使用-2023CICSN华中赛区pwn题逆向为例
文章目录 相关字节标识导入函数和导出函数找程序入口函数选项设置重命名CISCN2023华中赛区分区赛AWDIDA源码main 构造结构体sub_141B() 打开局部变量类型的视图增加变量类型重新定义变量类型再次设置变量类型并重新定义再次设置变量类型并重新定义再次设置变量类型并重新定义 设…...

安装虚拟机出现的一些问题
1、在重新打开软件之后出现闪退 解决:[WSL] 解决nsenter: cannot open /proc/320/ns/time: No such file or directory 问题 小白向-CSDN博客2、重新启动xrdp服务命令 解决: sudo systemctl restart xrdp3、将端口从3389改为3390,因为此前…...

Git+py+ipynb Usage
0.default config ssh-keygen -t rsa #之后一路回车,当前目录.ssh/下产生公私钥 cat ~/.ssh/id_rsa.pub #复制公钥到账号 git config --global user.email account_email git config --global user.name account_namebug of ipynb TqdmWarning: IProgress not found. Please …...

eBPF实践篇之环境搭建
文章目录 前言实验环境前置知识配置开发环境最后 前言 你好,我是醉墨居士,本次我们学习一下eBPF,我们基于libbpf-bootstrap来进行我们的eBPF程序开发🤗 实验环境 一台Debian12操作系统的计算机,我使用的是Debian12.…...

机器学习科普及学习路线
机器学习是一种让计算机系统通过从数据中学习来改进性能的方法。它的学习方法主要包括监督学习、无监督学习和强化学习。下面我将详细解释机器学习的概念、学习方法和学习路线。 1. 机器学习概念: 机器学习是一种人工智能的分支,旨在使计算机系统能够从…...
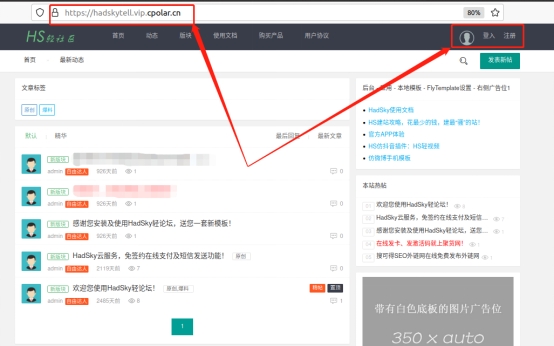
如何在本地电脑部署HadSky论坛并发布至公网可远程访问【内网穿透】
文章目录 前言1. 网站搭建1.1 网页下载和安装1.2 网页测试1.3 cpolar的安装和注册 2. 本地网页发布2.1 Cpolar临时数据隧道2.2 Cpolar稳定隧道(云端设置)2.3 Cpolar稳定隧道(本地设置)2.4 公网访问测试 总结 前言 经过多年的基础…...

Spring Boot 笔记 025 主界面
1.1 路由搭建 1.1.1 安装vue router npm install vue-router4 1.1.2 在src/router/index.js中创建路由器,并导出 import { createRouter, createWebHistory } from vue-router//导入组件 import LoginVue from /views/Login.vue import LayoutVue from /views/La…...

(done) Positive Semidefinite Matrices 什么是半正定矩阵?如何证明一个矩阵是半正定矩阵? 可以使用特征值
参考视频:https://www.bilibili.com/video/BV1Vg41197ew/?vd_source7a1a0bc74158c6993c7355c5490fc600 参考资料(半正定矩阵的定义):https://baike.baidu.com/item/%E5%8D%8A%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/2152711?frge_ala 看看半正定矩阵的…...

七、矩阵的初等变换
目录 -1. 介绍 0、增广矩阵: 1、初等变换的性质: 编辑2、矩阵初等变换的分类: 2.1 普通的行阶梯矩阵: 2.2 、行最简形矩阵: 2.3、标准形矩阵: 3、初等变换的定理: 4、初等变换的应用&…...

CSS background-size
background-size 菜鸟教程 CSS3 background-size 属性 MDN Web 开发技术>CSS:层叠样式表>background-size CSS的background 背景图片自动适应元素大小,实现img的默认效果 background-size:100% 100%; 在CSS中,background-size属性用…...

【机器学习】特征工程之特征选择
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...
