医疗器械之模糊算法(嵌入式部分)
模糊控制
所谓模糊控制,就是对难以用已有规律描述的复杂系统,采用自然语言(如大,中,小)加以描述,借助定性的,不精确的以及模糊的条件语句来表达,模糊控制是一种基于语言的智能控制。
传统的自动控制器的综合设计都要建立在被控对象准确的数学模型(即传递函数模型或状态空间模型)的基础上,但是实际上,很多系统的影响因素很多,通常找出精确的数学模型,这种情况下,模糊控制的诞生就显得意义重大,因为模糊控制不需要建立数学模型,不需要预先知道过程精确的数学模型。模糊控制与传统的PID控制,具有如下优点:
(1)无需知道被控对象的数学模型
(2)反映人类智慧思维的智能控制
(3)易被人们所接受,是一种语言变量控制器
(4)构造容易,从属于智能控制的范畴,尤其适用于非线性,时变,滞后系统的控制
(5)抗干扰能力强,响应速度快,并对系统参数的变化有较强的鲁棒性
1. 工作原理
把各种传感器测出的精确量转换为适用于模糊运算的模糊量,然后将这些量在模糊控制器中加以运算,最后再将运算结果中的模糊量转换为精确量,以便对各执行器进行具体的操作控制,这就说明在模糊控制中,存在着一个模糊量与精确量之间相互转化的问题,如下图所示:
模糊控制原理图如下图所示:
2. 模糊语言集
模糊语言集用表示,一般有={负大,负中,负小,零,正小,正中,正大},用模糊语言变量E来描述偏差,或者用符号表示:
负大:Negative Big,简称NB
负中:Negative Medium,简称NM
负小:Negative Small,简称NS
零:Zero,简称ZE
正小:Positive Small,简称PS
正中:Positive Medium,简称PM
正大:Positive Big,简称PB
3. 隶属函数
各参数相对应子集的隶属函数分别由不同的函数族决定,参数的相应子集指该参数被人为地划分成的等级所构成的一组模糊集合,相应子集的多少,由控制精度决定,例如,参数“温差”的相应子集可以是“正大,正中,负小,负大”,也可以是“正大,正中,正小,负小,负中,负大”,后者比前者模糊子集多,所以控制精度更高(在其他相同条件的情况下)。
常用的隶属函数如下所示。
(1)z型隶属度函数zmf
(2)S型隶属度函数smf
(3)三角形隶属度函数trimf
3.1 模糊控制数学基础
3.1.1 模糊控制集合的代数运算

3.1.2 模糊关系
(1)普通关系:两个集合中的元素之间是否有关联。
(2)模糊关系:两个模糊集合中的元素之间关联程度的多少。

3.1.3 模糊关系的合成

3.1.4 模糊推理

3.1.5 模糊决策
模糊决策(模糊判决,解模糊,清晰化):由模糊推理得到的结论或者操作是一个模糊向量,转化为确定值的过程。
(1)最大隶属度法
(2)加权平均判决法
(3)中位数法
3.1.6 模糊推理的运用

3.1.7 模糊控制系统的组成
与一般的计算机控制系统不同的是,模糊控制系统的控制器是模糊控制器,模糊控制器是基于模糊条件语句描述的语言控制规则,又称为模糊语言控制器。
输入输出变量
(1)模糊控制的输入变量通常取E或E,EC或E,EC,ER,分别构成所谓的一维,二维,三维模糊控制器,一般选择控制量的增量作为模糊控制器的输出变量。
(2)描述模糊控制器的输入,输出变量状态:负大(NB),负中(NM),负小(NS),零(O),正小(PS),正中(PM),正大(PB)。
(3)描述误差变量的词集一般取为:负大(NB),负中(NM),负小(NS),负零(NO),正零(PO),正小(PS),正中(PM),正大(PB)。
模糊变量E的赋值表
模糊控制规则
(1)条件语句的基本类型为:if A or B and C or D then E
例如水温控制规则之一为:若水温高或偏高,且温度上升快或较快,则加大冷水流量。
用条件语句表达为:if E=NB or NM and EC=NB or NM then U=PB
3.1.8 模糊控制算法的工程实现
在大型的模糊控制系统中常采用软件模糊推理法,模糊关系,模糊推理以及模糊判决的运算可以离线进行,最后得到模糊控制器输入量的量化等级E,EC与输出量即系统控制量的量化等级U之间的确定关系,这种关系通常称为控制表。
3.2 水位控制系统
3.2.1 控制目标
控制模型如下图所示,控制进水阀S1和出水阀S2,使水箱水位保持在目标水位O处。
3.2.2 控制规则
(1)若当前水位高于目标水位,则向外排水,差值越大,排水越快
(2)若当前水位低于目标水位,则向内注水,差值越大,注水越快
(3)若当前水位和目标水位相差很小,则保持排水速度和注水速度相等
注:建立模糊控制规则的基本思想:当误差大或较大时,选择控制量应该以尽快消除误差为主,而当误差较小时,选择控制量要防止超调,以系统的稳定性为主要出发点。
3.2.3 控制步骤
(1)我们选择目标水位和当前水位的差值e作为观察量,选取阀门开度u为控制量。
(2)将偏差e划分为5个模糊集,负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB),e为负表示当前水位低于目标水位,e为正表示当前水位高于目标水位。设定e的取值范围为[-3,3]。
此时偏差e对应的模糊表如下表所示。
-3 -2 -1 0 1 2 3
PB 0 0 0 0 0 0.5 1
PS 0 0 0 0.5 1 0.5 0
ZO 0 0 0.5 1 0.5 0 0
NS 0 0.5 1 0.5 0 0 0
NB 1 0.5 0 0 0 0 0
(3)将控制量u划分为5个模糊集,负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB),u为负表示增大进水阀门S1的开度(同时减小出水阀门S2的开度),u为正表示减小进水阀门S1的开度(同时增大出水阀门S2的开度)。设定u的取值范围为[-4,4],隶属度函数如下。
此时控制量u对应的模糊表如下表所示。
-4 -3 -2 -1 0 1 2 3 4
PB 0 0 0 0 0 0 0 0.5 1
PS 0 0 0 0 0 0.5 1 0.5 0
ZO 0 0 0 0.5 1 0.5 0 0 0
NS 0 0.5 1 0.5 0 0 0 0 0
NB 1 0.5 0 0 0 0 0 0 0
(4)制定模糊规则:模糊规则的制定是模糊控制的核心内容,控制性能的好坏很大程度上由模糊规则决定,目前主要是根据经验来制定相应的规则
若e负大,则u负大
若e负小,则u负小
若e为零,则u为零
若e正小,则u正小
若e正大,则u正大
(6)进行模糊决策:最终需要的控制量u即为模糊控制的输出,u可由偏差矩阵e和模糊关系矩阵R合成得到
(7)控制量的反模糊化
我们模糊决策得到的控制量u是一个矩阵,并不能直接应用在工程上,因此需要将u解释为实际中的特定行为,即反模糊化操作。目前常用的反模糊化方法有以下几种:
最大隶属度法:应用于计算简单控制要求不高场合
重心法:可以使得输出更平滑
加权平均法:工业上应用最广泛
3.3 模糊控制算法实现
3.3.1 MATLAB代码
clc
clear%创建模糊控制器
a = newfis(‘fuzzy tank’);%输入变量
a = addvar(a,‘input’,‘e’,[-3,3]); %设置变量e为输入且定义域[-3,3]
a = addmf(a,‘input’,1,‘NB’,‘zmf’,[-3,-1]); %Z型隶属度函数
a =addmf(a,‘input’,1,‘NS’,‘trimf’,[-3,-1,1]); %三角形隶属度函数
a =addmf(a,‘input’,1,‘ZO’,‘trimf’,[-2,0,2]); %三角形隶属度函数
a =addmf(a,‘input’,1,‘PS’,‘trimf’,[-1,1,3]); %三角形隶属度函数
a = addmf(a,‘input’,1,‘PB’,‘smf’,[1,3]); %S型隶属度函数%输出变量
a = addvar(a,‘output’,‘u’,[-4,4]); %设置变量u为输出且定义域[-4,4]
a = addmf(a,‘output’,1,‘NB’,‘zmf’,[-4,-2]); %Z型隶属度函数
a =addmf(a,‘output’,1,‘NS’,‘trimf’,[-4,-2,0]); %三角形隶属度函数
a =addmf(a,‘output’,1,‘ZO’,‘trimf’,[-2,0,2]); %三角形隶属度函数
a =addmf(a,‘output’,1,‘PS’,‘trimf’,[0,2,4]); %三角形隶属度函数
a = addmf(a,‘output’,1,‘PB’,‘smf’,[2,4]); %S型隶属度函数%建立模糊规则
rulelist=[1 1 1 1;
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];
a = addrule(a,rulelist);%设置反模糊化算法
a1 = setfis(a,‘DefuzzMethod’,‘mom’); %采用最大隶属度平均法进行反模糊化
writefis(a1,‘tank’); %保存tank文件
a2 = readfis(‘tank’); %读取tank文件%绘制图像figure(1); plotfis(a2); %绘制模糊控制器结构figure(2); plotmf(a,‘input’,1); %绘制输入隶属度函数图像figure(3); plotmf(a,‘output’,1); %绘制输出隶属度函数图像%打开模糊调试器
showrule(a);
ruleview(‘tank’);
MATLAB仿真结果如下图所示。
3.3.2 C语言代码
#include #include #include #define N 7 //定义量化论域模糊子集的个数//模糊语言定义#define NB -3#define NM -2#define NS -1#define ZO 0#define PS 1#define PM 2#define PB 3struct
{
//规则表
int rule[ N ][ N ] ; //模糊规则表
//隶属度函数
char f_type_e ; //e的隶属度函数类型
char f_type_de ; //de的隶属度函数类型
char f_type_u ; //u的隶属度函数类型
float paras_e[ 3N ] ; //e的隶属度函数的参数
float paras_de[ 3N ] ; //de的隶属度函数的参数
float paras_u[ 3N ] ; //u的隶属度函数的参数
//模糊运算参数
float Ke ; //Ke=n/emax,量化论域为[-3,-2,-1,0,1,2,3]
float Kde ; //Ke=n/demax,量化论域为[-3,-2,-1,0,1,2,3]
float Ku ; //Ke=umax/n,量¢化论域为[-3,-2,-1,0,1,2,3]
float umax ; //输出的上限
float emax ; //误差基本论域上限
float demax ; //误差变化率基本论域的上限
//控制目标参数
float target ; //控制目标
float actual ; //实际值
float e ; //误差
float e_pre ; //上一次的误差
float de ; //误差的变化率
}fuzzy;/*******************************************************
Name :trimf
Function :三角隶属度函数
Parameter :
x:自变量
(a,b,c):定义域
Return :结果
/float trimf( float x, float a, float b, float c ){
float u ;
if( ( x>=a )&&( x<=b ) )
u = ( x-a )/( b-a ) ;
else if( ( x>b )&&( x<=c ) )
u = ( c-x )/( c-b ) ;
else
u = 0 ;
return u ;
}/
Name :gaussmf
Function :正态隶属度函数
Parameter :
x:自变量
ave:均值
sigma:方差
Return :结果
/float gaussmf( float x, float ave, float sigma ){
float u ;
if( sigma<0 )
printf(“方差不允许小于0\n”);
else
u = exp( -pow( ( ( x-ave )/sigma ), 2 ) ) ;
return u ;
}/
Name :trapmf
Function :梯形隶属度函数
Parameter :
x:自变量
(a,b,c,d):定义域
Return :结果
*******************************************************/float trapmf( float x, float a, float b, float c, float d ){
float u ;
if( ( x>=a )&&( xelse if( ( x>=b )&&( x
**
相关文章:

医疗器械之模糊算法(嵌入式部分)
模糊控制 所谓模糊控制,就是对难以用已有规律描述的复杂系统,采用自然语言(如大,中,小)加以描述,借助定性的,不精确的以及模糊的条件语句来表达,模糊控制是一种基于语言的…...
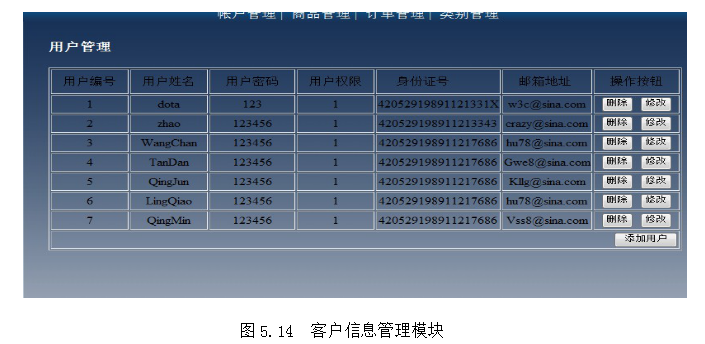
网上销售笔记本系统
技术:Java、JSP等摘要:本文讲述了基于B/S模式的笔记本电脑在线销售系统的设计与实现。所谓的笔记本电脑在线销售系统是通过网站推广互联企业的笔记本电脑和技术服务,并使客户随时可以了解企业和企业的产品,为客户提供在线服务和订…...
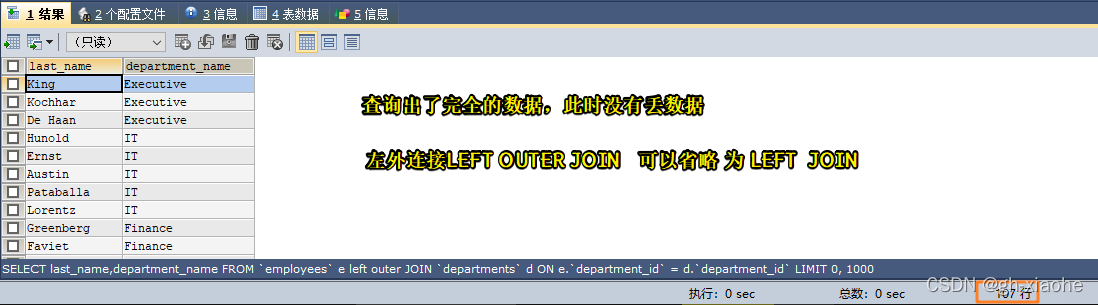
MySQL基础查询操作
文章目录🚏 Select语句🚀 一、SQL底层执行原理🚬 (一)、查询的结构🚬 (二)、SQL语句的执行过程🚭 1、WHERE 为什么不包含聚合函数的过滤条件?(面试…...

English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三
English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [ʌ]&…...
Condition 源码解读
一、Condition 在并发情况下进行线程间的协调,如果是使用的 synchronized 锁,我们可以使用 wait/notify 进行唤醒,如果是使用的 Lock 锁的方式,则可以使用 Condition 进行针对性的阻塞和唤醒,相较于 wait/notify 使用…...
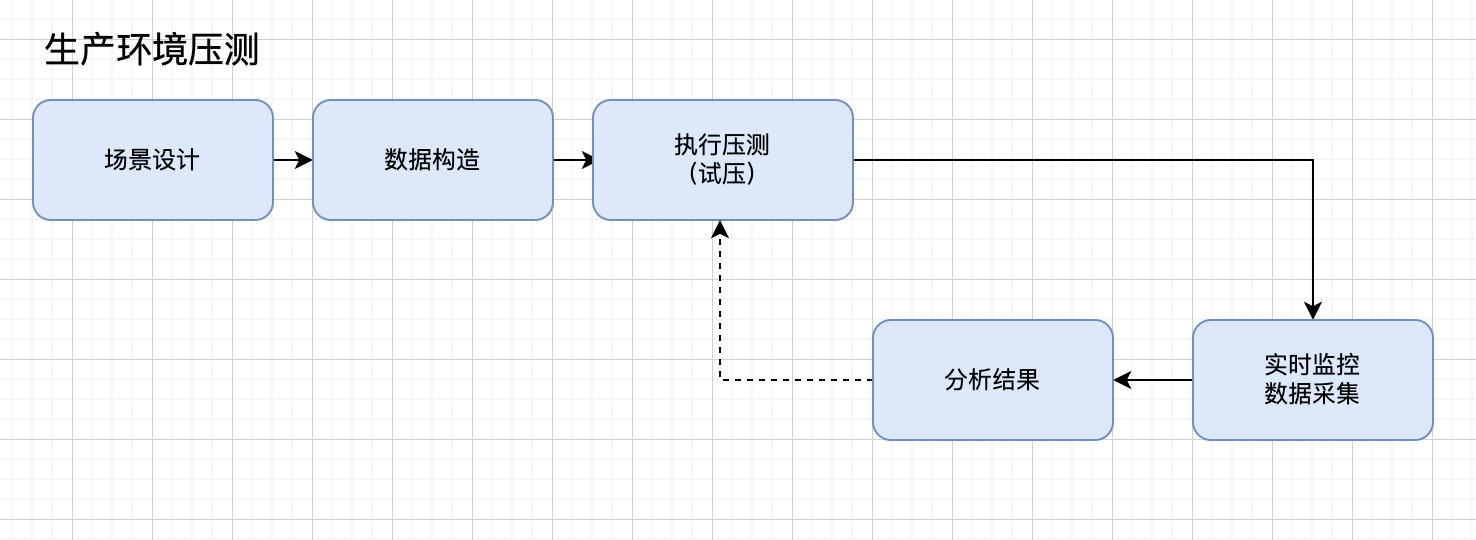
看完这篇入门性能测试
大家好,我是洋子。最近组内在进行服务端高并发接口的性能压测工作,起因是2023年2月2日,针对胡某宇事件进行新闻发布会直播,几十万人同时进入某媒体直播间,造成流量激增 从监控上可以看出,QPS到达某峰值后&…...

推导部分和——带权并查集
题解: 带权并查集 引言: 带权并查集是一种进阶的并查集,通常,结点i的权值等于结点i到根节点的距离,对于带权并查集,有两种操作需要掌握——Merge与Find,涉及到路径压缩与维护权值等技巧。 带…...
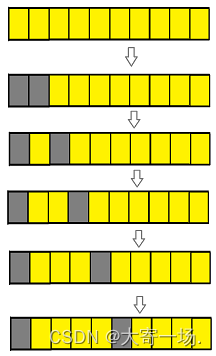
费解的开关/翻硬币
🌱博客主页:大寄一场. 🌱系列专栏: 算法 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 题目:费解的开关 你玩过“拉灯”游戏吗? 25盏灯排成一个 55 的方形。 每一个灯都有一个开关&…...
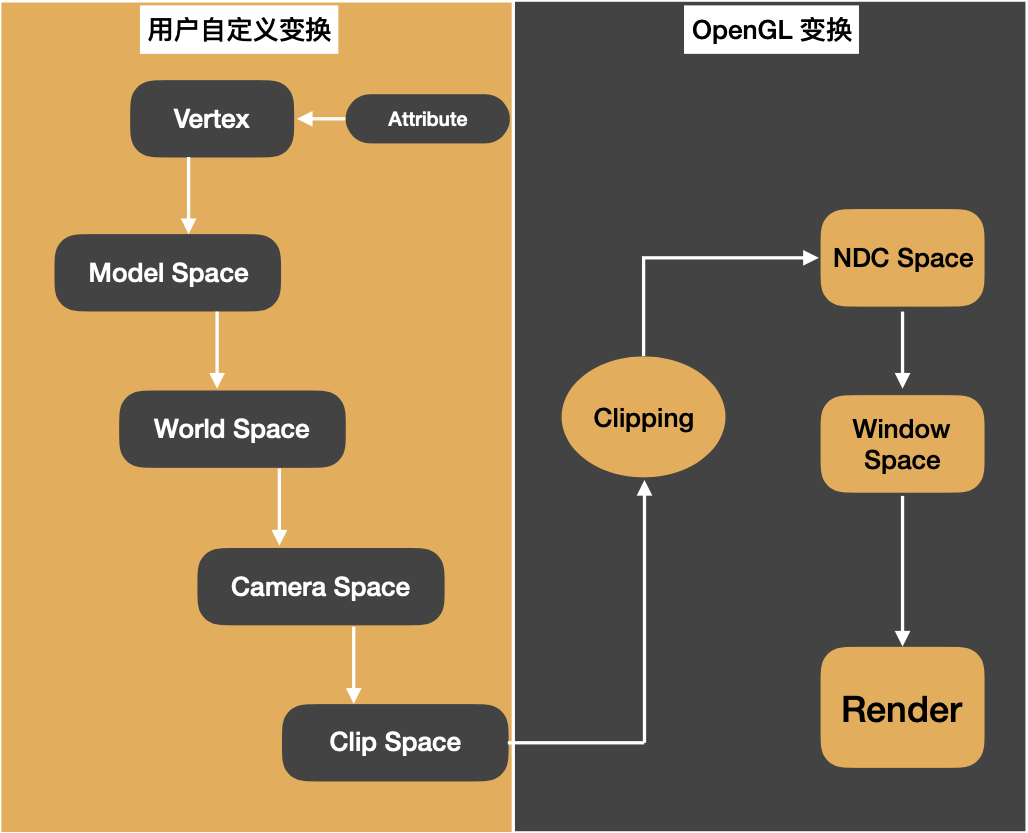
OpenGL中的坐标系
1、2D笛卡尔坐标系2D笛卡尔坐标系跟我们高中的时候学习的坐标系一样,是由x、y决定的。2、3D笛卡尔坐标系3D笛卡尔坐标系坐标由x、y、z决定,满足右手定则。3、视口glViewport(GLint x,GLint y,GLsizei width,GLsizei height)窗口和视口大小可以相同&#…...

Spring——Spring介绍和IOC相关概念
Spring是以Spring Framework为核心,其余的例如Spring MVC, Spring Cloud,Spring Data,Spring Security SpringBoot的基础都是Spring Framework。 Spring Boot可以在简化开发的基础上加速开发。 Spring Cloud分布式开发 Spring有…...

A+B Problem
AB Problem 题目描述 输入两个整数 a,ba, ba,b,输出它们的和(∣a∣,∣b∣≤109|a|,|b| \le {10}^9∣a∣,∣b∣≤109)。 注意 Pascal 使用 integer 会爆掉哦!有负数哦!C/C 的 main 函数必须是 int 类型,…...
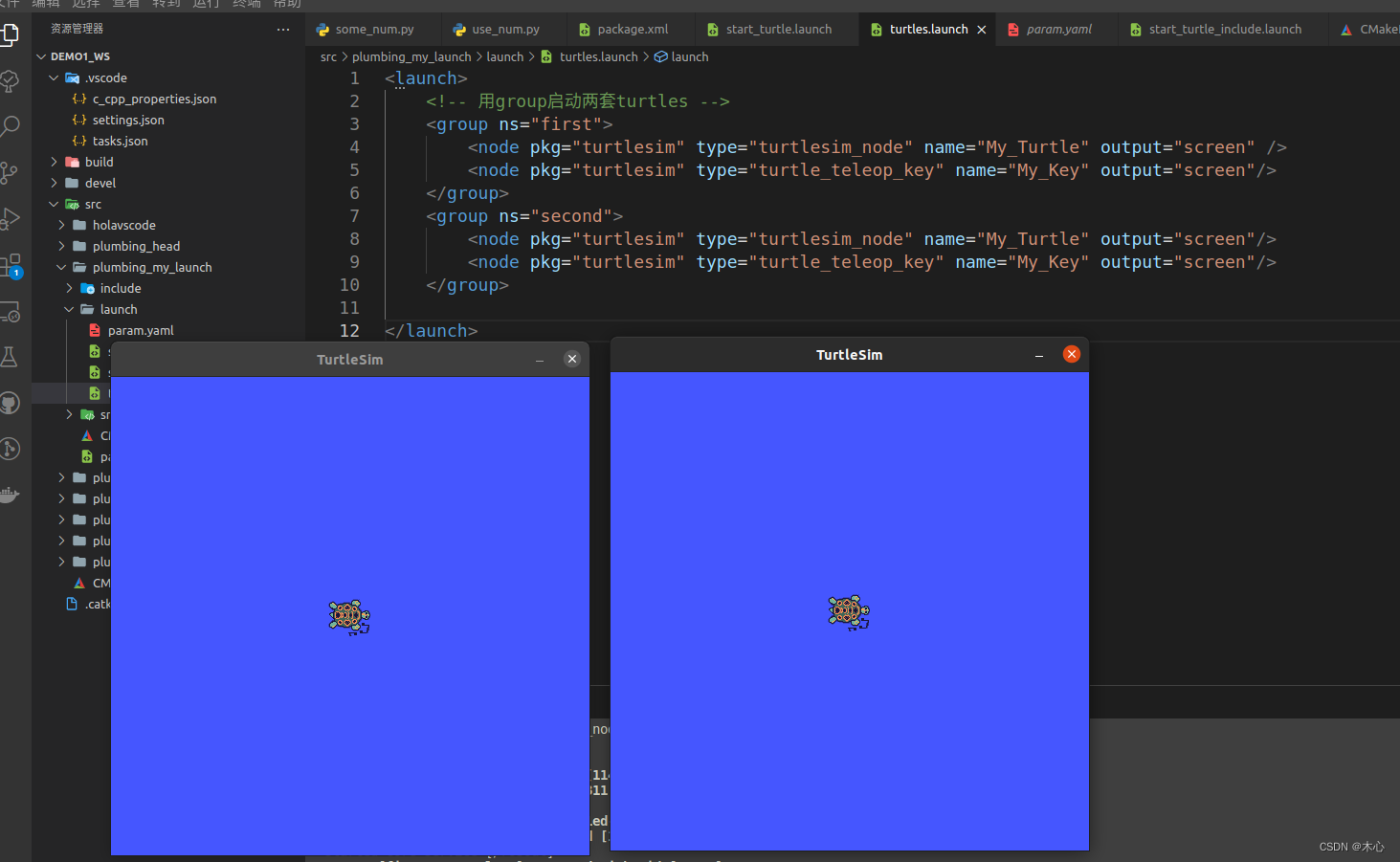
【ROS学习笔记11】ROS元功能包与launch文件的使用
【ROS学习笔记11】ROS元功能包与launch文件的使用 文章目录【ROS学习笔记11】ROS元功能包与launch文件的使用前言一、ROS元功能包二、ROS节点运行管理launch文件2.1 launch文件标签之launch2.2 launch文件标签之node2.3 launch文件标签之include2.4 launch文件标签之remap2.5 l…...

【python】
print函数 同时输出多行变量 print(a, b, sep\n) (23条消息) python3 中print函数参数详解,print(*values, sep , end\n, filesys.stdout, flushFalse)中参数介绍_sep,_phantom-dapeng的博客-CSDN博客 input() 输入浮点数,不能用int(input()) int()…...
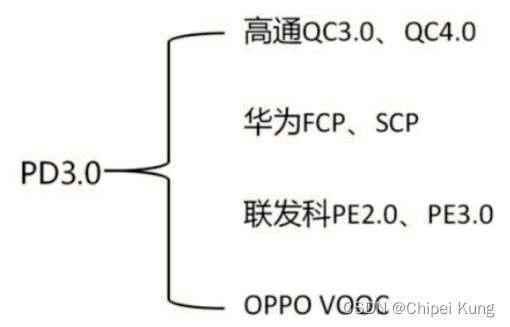
充电协议: 快充协议,如何选充电宝?
快充协议(存在两种:电压; 电流) 目前市面上的快充技术大多遵循2个技术方向: 以高通QC、联发科PEP、华为FCP为首的高压低电流快充技术; 另一种就是以OPPO的VOOC以及华为SCP为首的低电压大电流快充技术。 目前常见的快充标准还有三星AFC、联发…...
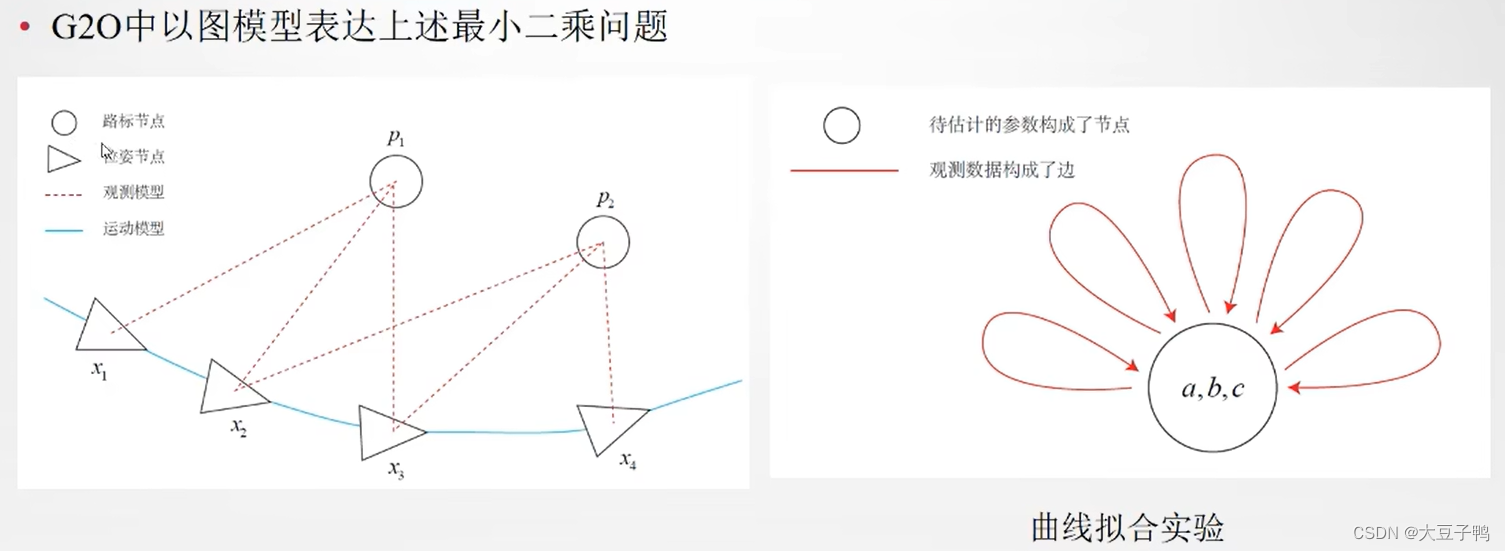
视觉SLAM十四讲ch6 非线性优化笔记
视觉SLAM十四讲ch6 非线性优化笔记本讲目标上讲回顾状态估计问题非线性最小二乘Gauss-Newton:高斯牛顿Levenburg-Marquadt:列文伯格-马夸尔特小结实践:CERES实践:G2O本讲目标 理解最小二乘法的含义和处理方式。 理解Gauss-Newton…...

Nikto工具使用指南
NiktoNikto是一款开源网站服务器扫描器,使用Perl开发,可以对服务器进行全面扫描,包括6400多个潜在危险的文件/cgi(通用网关接口(Common Gateway Interface)),废话不多说,直接上命令:基本测试&am…...
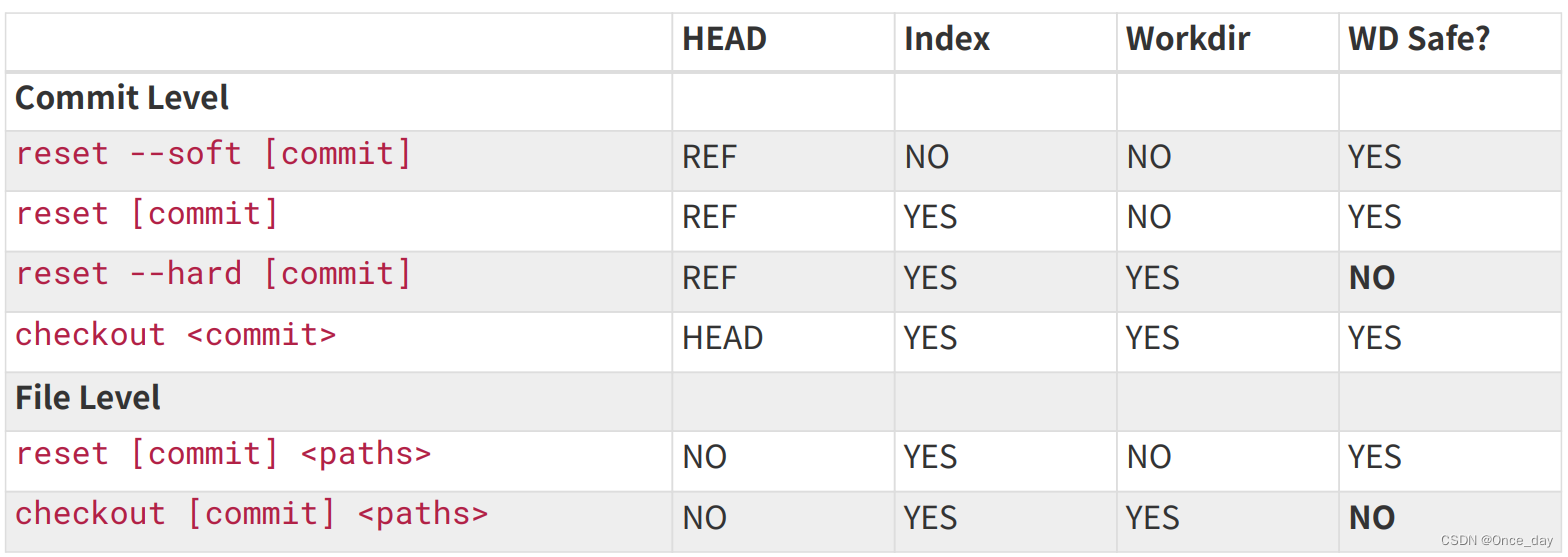
Git(4)之基本工具
Git基础之基本工具 Author:onceday date:2023年3月5日 满满长路有人对你微笑过嘛… windows安装可参考文章:git简易配置_onceday_CSDN博客 參考文档: 《progit2.pdf》,Progit2 Github。《git-book.pdf》 文章目录…...

好书推荐。
个人喜欢看传记,散文,历史等 二战名人传记,苏联列宁,朱可夫,斯大林等 英国首相丘吉尔,美国富兰克林,中国毛泽东等 创业:比尔盖,扎克伯格,苹果公司创始人乔…...

[Pytorch]DataSet和DataLoader逐句详解
将自己的数据集引入Pytorch是搭建属于自己的神经网络的重要一步,这里我设计了一个简单的实验,结合这个实验代码,我将逐句教会大家如何将数据引入DataLoader。 这里以目标检测为例,一个batch中包含图片文件、先验框的框体坐标、目标…...
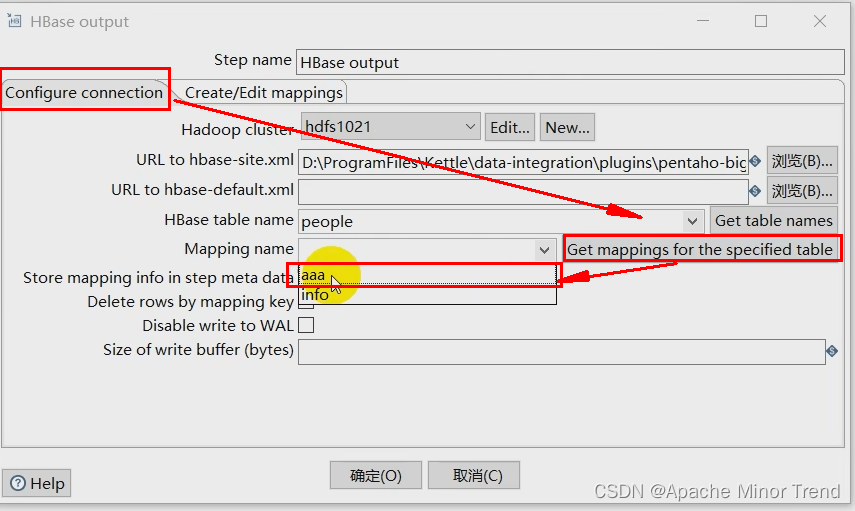
【Kettle-佛系总结】
Kettle-佛系总结Kettle-佛系总结1.kettle介绍2.kettle安装3.kettle目录介绍4.kettle核心概念1.转换2.步骤3.跳(Hop)4.元数据5.数据类型6.并行7.作业5.kettle转换1.输入控件1.csv文件输入2.文本文件输入3.Excel输入4.XML输入5.JSON输入6.表输入2.输出控件…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
