C++/数据结构:AVL树
目录
一、AVL树的概念
二、AVL树的实现
2.1节点定义
2.2节点插入
三、AVL树的旋转
3.1新节点插入较高左子树的左侧:右单旋
3.2新节点插入较高右子树的右侧:左单旋
3.3新节点插入较高左子树的右侧---左右:先左单旋再右单旋
3.4新节点插入较高右子树的左侧---右左:先右单旋再左单旋
四、AVL树的性能
一、AVL树的概念
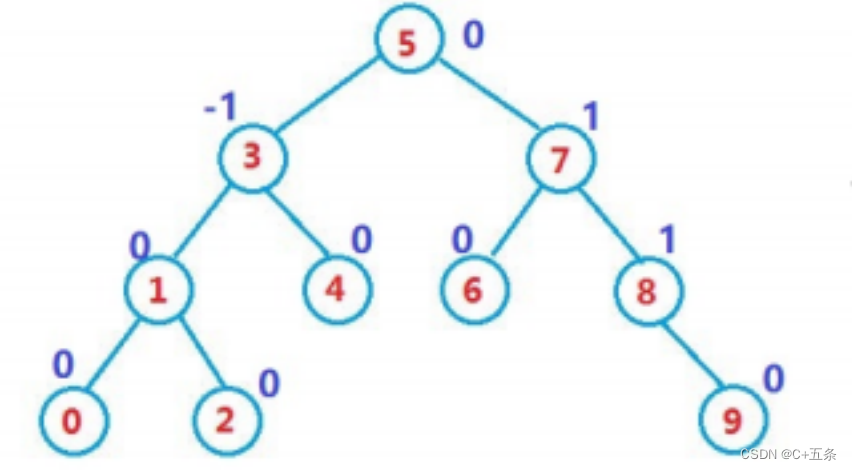
二、AVL树的实现
2.1节点定义
template <class K,class V>
class AVLtreeNode
{AVLtreeNode<K, V>* _left;AVLtreeNode<K, V>* _right;AVLtreeNode<K, V>* _parent;pair<K, V> _kv;int bf;AVLtreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), bf(0){}
};2.2节点插入
bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;} }cur = new Node(kv);if (parent->_kv.first>cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;} cur->_parent = parent;//调整avl树的结构,处理parent的平衡因子while (parent){if (parent->left == cur){parent->bf--;}else if (parent->right == cur){parent->bf++;}//不断向上更改avl树中的bf平衡因子if (parent->_bf == 1 || parent->_bf == -1){//更新去上面的父节点的bfparent = parent->_parent;cur = cur->parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转处理//单旋if (parent->_bf == 2 && cur->_bf == 1)//右边高 {RotateL(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == -1)//左边高{RotateR(parent);//右单旋}//双旋处理else if (parent->_bf==-2&&cur->_bf==1)//左边高的右边高,先左旋再右旋{RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent)//右边高的左边高,先右旋再左旋}else{assert(false);}break;}else{assert(false);}}return true;}三、AVL树的旋转
3.1新节点插入较高左子树的左侧:右单旋
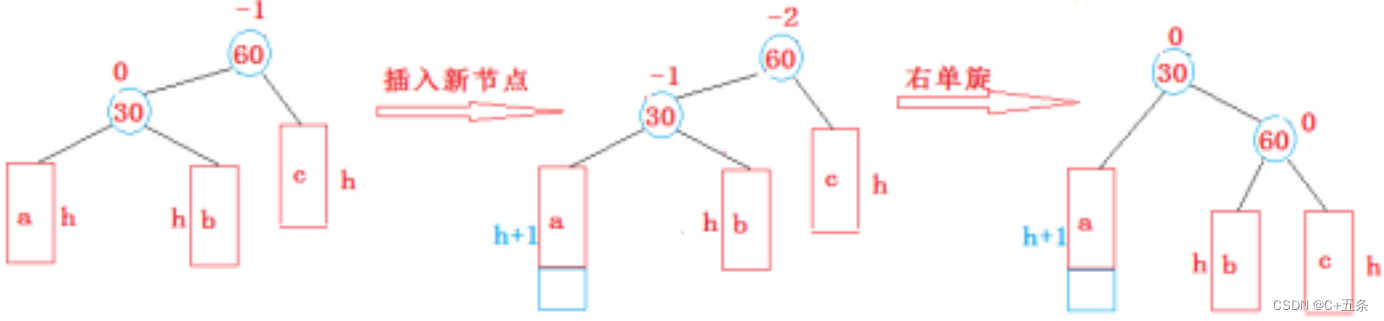
void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;Node* pparent = parent->_parent;parent->_left = subLR;if (subLR) subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left == subL;}else{pparent->_right == subL;}subL->_parent = pparent;}subL->_bf = parent->_bf = 0;return true;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent); if (bf == 1)//左边高的右边高,新增节点在右{parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == -1)//新增节点在左{parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0 ;}else if (bf == 0)//本身就是新增节点直接导致出现左边高的右边高{parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}}3.2新节点插入较高右子树的右侧:左单旋
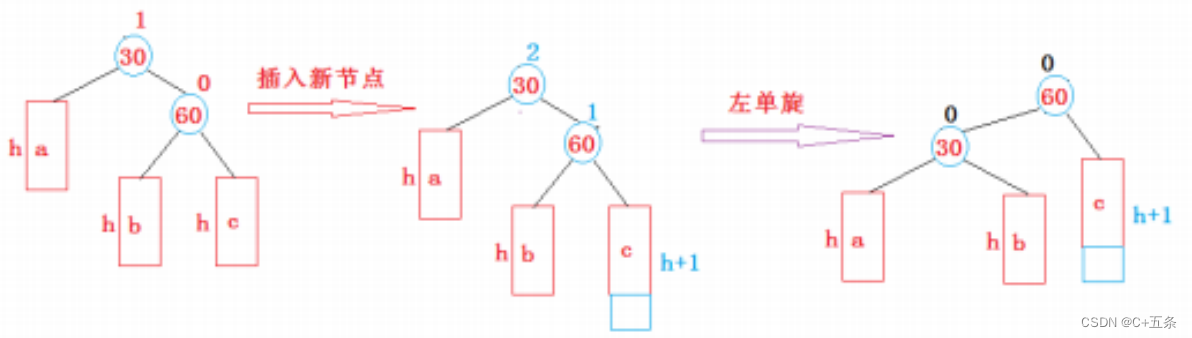
和右单旋的思路以及实现方式大相径庭。只需略微改动。
void RotateL(Node* parent)//左单旋{Node* subR = parent->right;Node* subRL = subR->left;Node* pparent = parent->_parent;parent->right = subRL;if(subRL)subRL->_parent = parent;subR->left = parent;parent->_parent = subR;if (pparent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}parent->_bf = subR->_bf = 0;}3.3新节点插入较高左子树的右侧---左右:先左单旋再右单旋
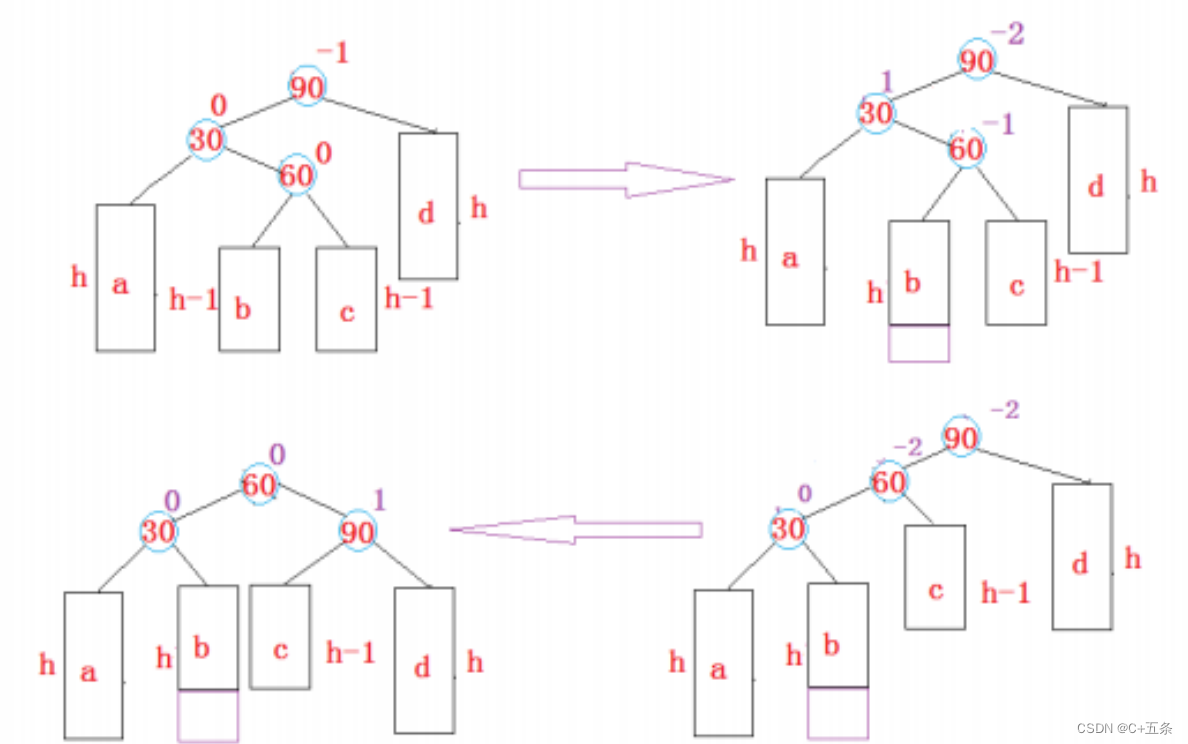
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent); if (bf == 1)//左边高的右边高,新增节点在右{parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == -1)//新增节点在左{parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0 ;}else if (bf == 0)//本身就是新增节点直接导致出现左边高的右边高{parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}}3.4新节点插入较高右子树的左侧---右左:先右单旋再左单旋
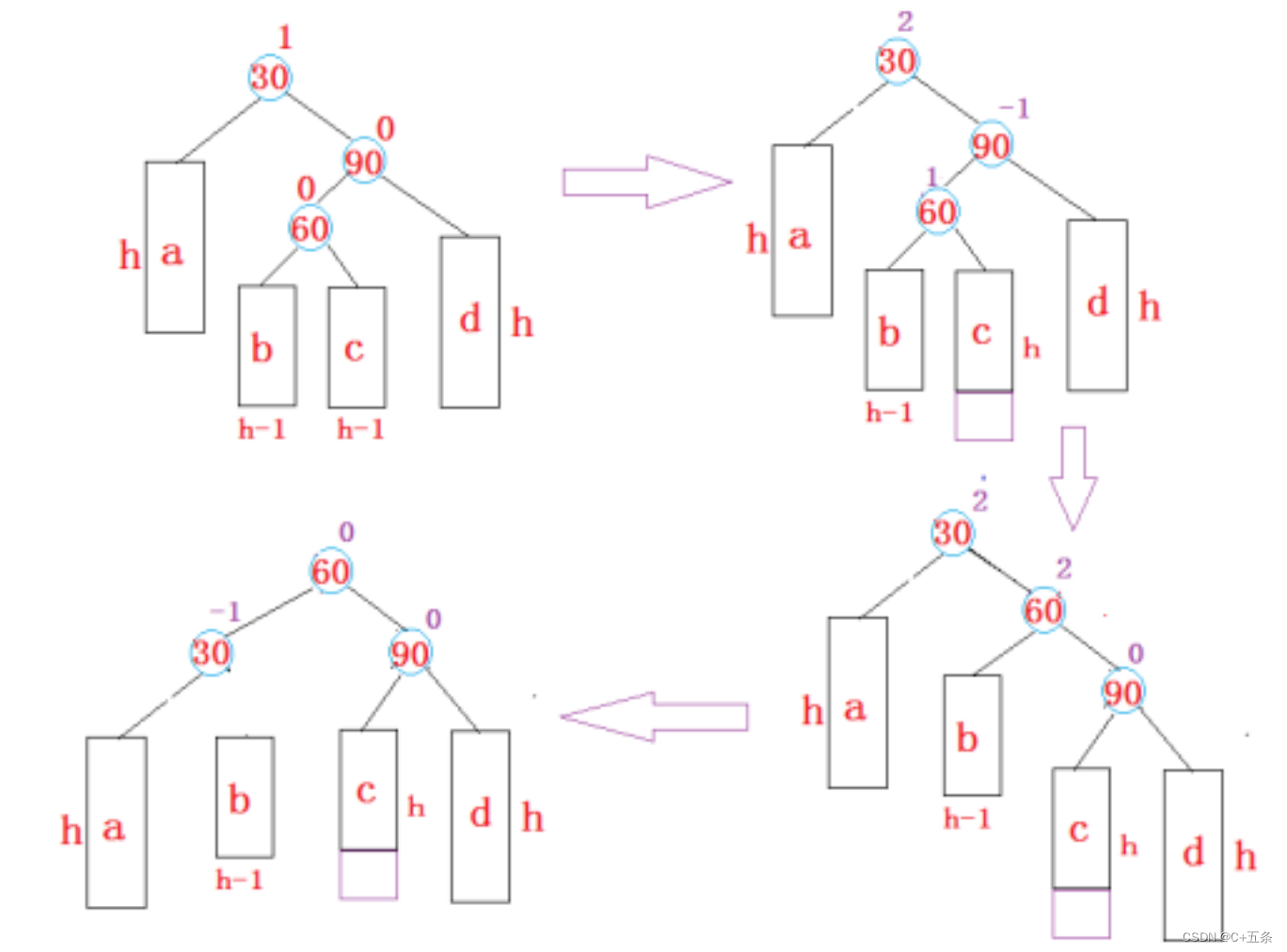
参考右左双旋
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL =subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else if (bf == -1){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}else if (bf == 0){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 0;}else{assert(false);}}四、AVL树的性能
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不 错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这 样可以保证查询时高效的时间复杂度,即$log_2 (N)$。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时, 有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数 据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:

C++/数据结构:AVL树
目录 一、AVL树的概念 二、AVL树的实现 2.1节点定义 2.2节点插入 三、AVL树的旋转 3.1新节点插入较高左子树的左侧:右单旋 3.2新节点插入较高右子树的右侧:左单旋 3.3新节点插入较高左子树的右侧---左右:先左单旋再右单旋 3.4新节点插…...

Mysql数据库_max_allowed_packet参数详解
本文目录 参数含义查看max_allowed_packet参数值修改max_allowed_packet参数值修改配置文件方式(需要重启)直接修改配置方式(不需要重启)注意事项 出现场景 参数含义 max_allowed_packet参数指的是MySQL服务端或者客户端接收一次…...

【数仓】Hadoop集群配置常用参数说明
Hadoop集群中,需要配置的文件主要包括四个 配置核心Hadoop参数: 编辑core-site.xml文件,设置Hadoop集群的基本参数,如文件系统、Hadoop临时目录等。 配置HDFS参数: 编辑hdfs-site.xml文件,设置HDFS的相关参…...
【go从入门到精通】什么是go?为什么要选择go?
go的出生: go语言(或Golang)是Google开发的开源编程语言,诞生于2006年1月2日下午15点4分5秒,于2009年11月开源,2012年发布go稳定版。Go语言在多核并发上拥有原生的设计优势,Go语言从底层原生支持…...

MySQL篇—执行计划介绍(第二篇,总共三篇)
☘️博主介绍☘️: ✨又是一天没白过,我是奈斯,DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux,也在积极的扩展IT方向的其他知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章,并且也会默默的点赞收藏加关注❣…...
nest.js使用nest-winston日志一
nest-winston文档 nest-winston - npm 参考:nestjs中winston日志模块使用 - 浮的blog - SegmentFault 思否 安装 cnpm install --save nest-winston winstoncnpm install winston-daily-rotate-file 在main.ts中 import { NestFactory } from nestjs/core; im…...
)
LeetCode刷题笔记之二叉树(四)
一、二叉搜索树的应用 1. 700【二叉搜索树中的搜索】 题目: 给定二叉搜索树(BST)的根节点 root 和一个整数值 val。你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。代码&a…...
【MATLAB源码-第150期】基于matlab的开普勒优化算法(KOA)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 开普勒优化算法(Kepler Optimization Algorithm, KOA)是一个虚构的、灵感来自天文学的优化算法,它借鉴了开普勒行星运动定律的概念来设计。在这个构想中,算法模仿行星围绕太阳的…...
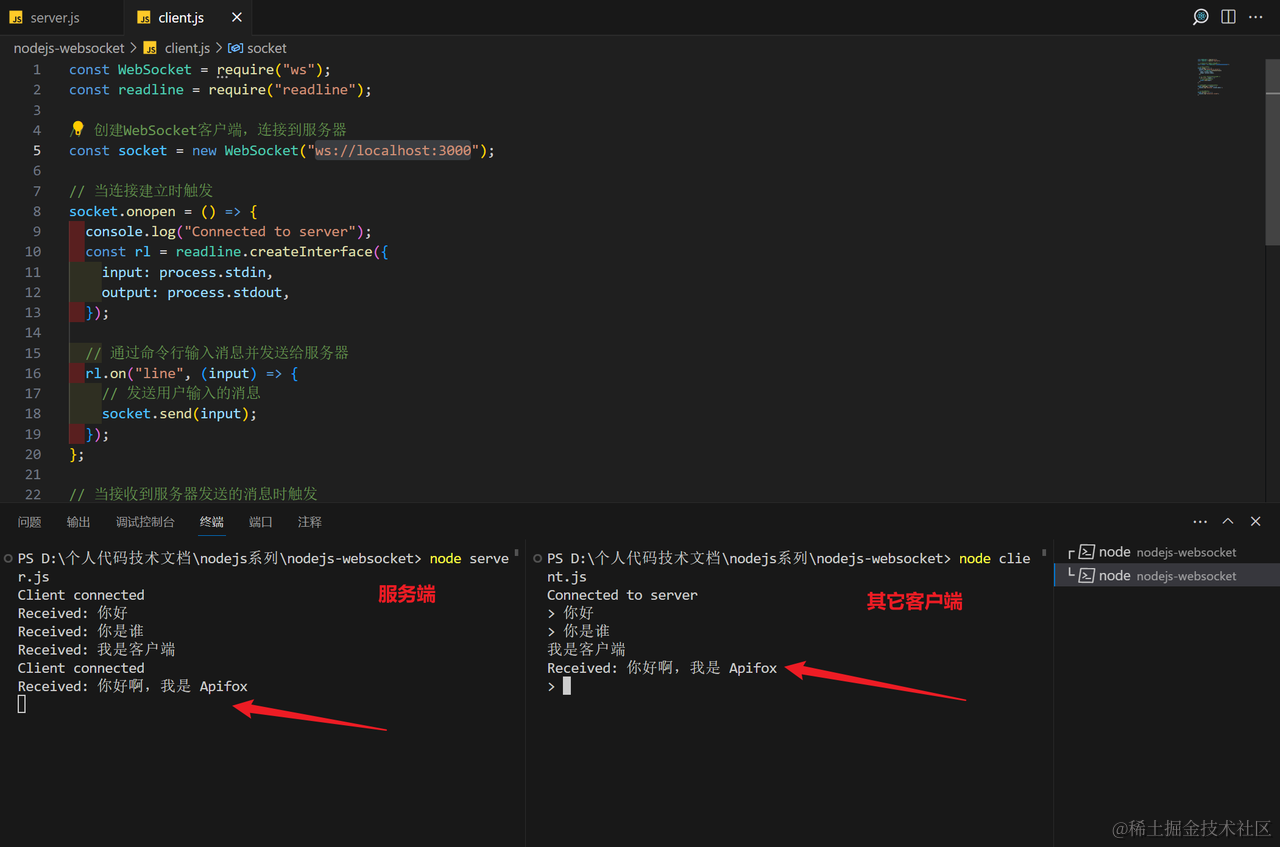
最佳实践:Websocket 长连接状态如何保持
WebSocket 是一种支持通过单个 TCP 连接进行全双工通信的协议,相较于传统的 HTTP 协议,它更适合需要实时交互的应用场景。此协议在现代 Web 应用中扮演着至关重要的角色,尤其是在需要实时更新和通信的场合下维持持久连接。本文将探讨 WebSock…...

Unity AStar寻路算法与导航
在游戏开发中,寻路算法是一个非常重要的部分,它决定了游戏中角色的移动路径。Unity作为一款流行的游戏开发引擎,提供了许多内置的寻路算法,其中最常用的就是AStar算法。AStar算法是一种基于图的搜索算法,通过启发式搜索…...

JavaScript最新实现城市级联操作,json格式的数据
前置知识: <button onclick"doSelect()">操作下拉列表</button><hr>学历:<select id"degree"><option value"0">--请选择学历--</option><option value"1">专科<…...

SD NAND:为车载显示器注入智能与安全的心脏
SD NAND 在车载显示器的应用 在车载显示器上,SD NAND(Secure Digital NAND)可以有多种应用,其中一些可能包括: 导航数据存储: SD NAND 可以用于存储地图数据、导航软件以及车载系统的相关信息。这有助于提…...

矩阵的对角化
概述 对角化矩阵是线性代数中的一个重要概念,它涉及将一个方阵转换成一个对角阵,这个对角阵与原矩阵相似,其主要对角线上的元素为原矩阵的特征值。这样的转换简化了很多数学问题,特别是线性动力系统的求解和矩阵的幂运算。下面是…...

React编写组件时,如何省略.tsx后缀
省略.tsx后缀 当tsconfig.json配置了,需要重启后才会生效 {"compilerOptions": {"allowJs": true,"jsx": "react-jsx",} }当进行以上配置后,导入组件时添加后缀,Eslint报错如下: An im…...

移动端的React项目中如何配置自适应和px转rem
创建项目 create-react-app project-name 启动项目 npm start 下载自适应和px转rem的插件 自适应的: npm install lib-flexible --save px转rem的:npm install postcss-pxtorem5.1.1 --save-dev 创建craco.config.js配置文件 在package.json中…...

TypeScript 结合 React 开发时候 , React.FunctionComponent 解释
在 TypeScript 结合 React 开发时,React.FC(或 React.FunctionComponent)是一个泛型类型,它用于定义函数组件的类型。这个类型定义了函数组件的结构和预期行为,并且提供了泛型支持,以便你可以指定组件 prop…...
#困难,想不到)
2280. 最优标号(最小割,位运算)#困难,想不到
活动 - AcWing 给定一个无向图 G(V,E),每个顶点都有一个标号,它是一个 [0,2^31−1] 内的整数。 不同的顶点可能会有相同的标号。 对每条边 (u,v),我们定义其费用 cost(u,v) 为 u 的标号与 v 的标号的异或值。 现在我们知道一些顶点的标号…...
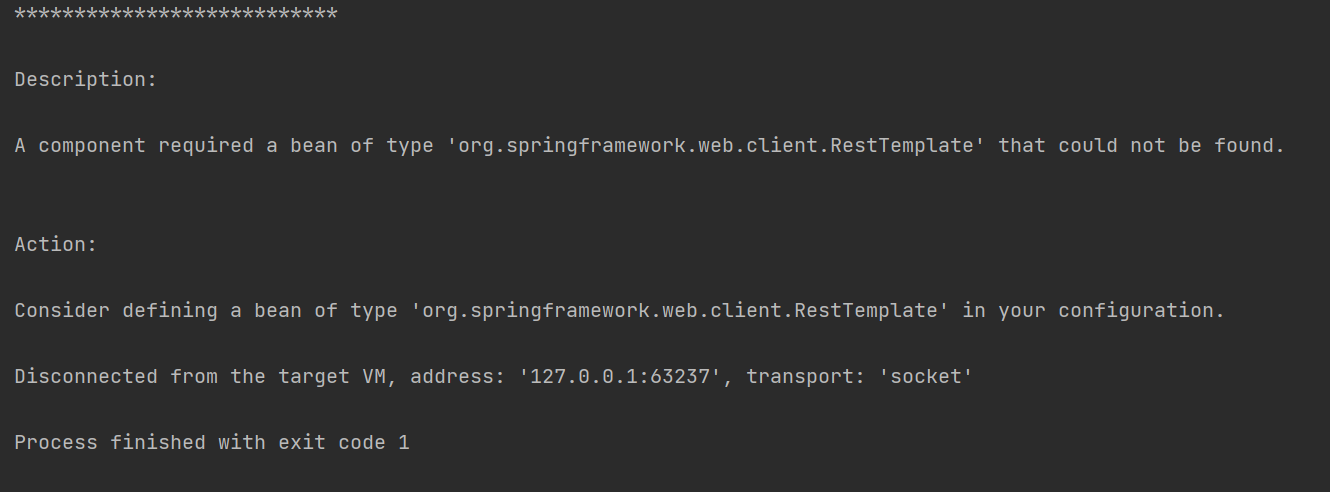
RestTemplate启动问题解决
⭐ 作者简介:码上言 ⭐ 代表教程:Spring Boot vue-element 开发个人博客项目实战教程 ⭐专栏内容:个人博客系统 ⭐我的文档网站:http://xyhwh-nav.cn/ RestTemplate启动问题解决 问题:在SpringCloud架构项目中配…...

Docker部署前后端服务示例
使用Docker部署js前端 1.创建Dockerfile 在项目跟目录下创建Dockerfile文件: # 使用nginx作为基础镜像 FROM nginx:1.19.1# 指定工作空间 WORKDIR /data/web# 将 yarn build 打包后的build文件夹添加到工作空间 ADD build build# 将项目必要文件添加到工作空间&a…...
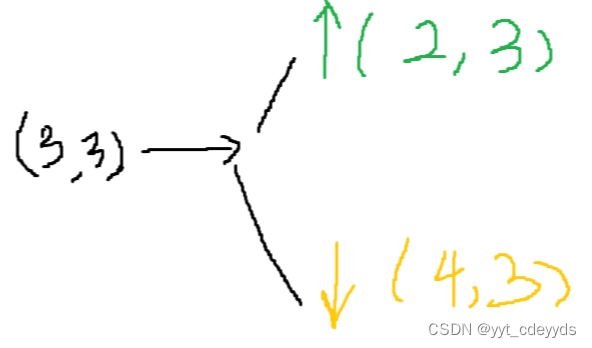
方格分割644--2017蓝桥杯
1.用dfs解决,首先这题的方格图形就很像一个走迷宫的类型,迷宫想到dfs,最中心点视为起点,起点有两个小人在这个方格里面对称行动,直到走出迷宫(一个人走出来了另一个人就也走出来了,而走过的点会…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
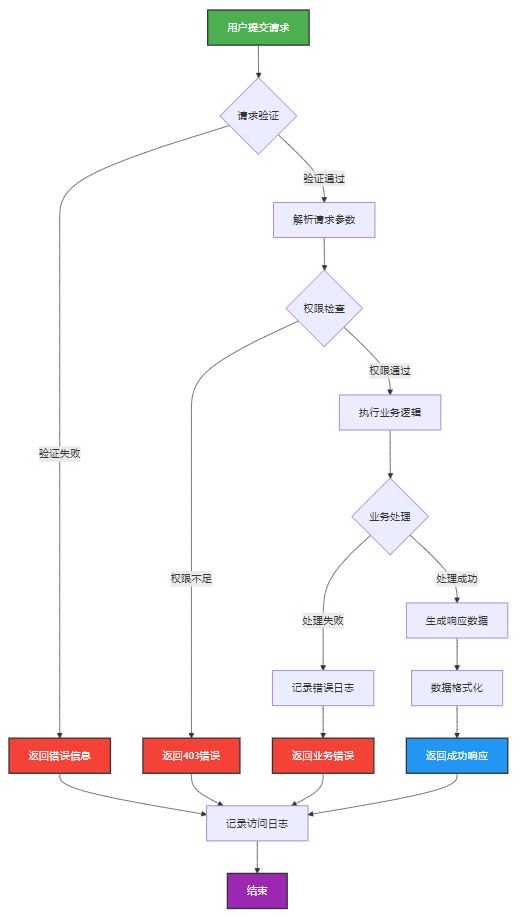
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...
