曲线生成 | 图解Dubins曲线生成原理(附ROS C++/Python/Matlab仿真)
目录
- 0 专栏介绍
- 1 什么是Dubins曲线?
- 2 Dubins曲线原理
- 2.1 坐标变换
- 2.2 单步运动公式
- 2.3 曲线模式
- 3 Dubins曲线生成算法
- 4 仿真实现
- 4.1 ROS C++实现
- 4.2 Python实现
- 4.3 Matlab实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 什么是Dubins曲线?
Dubins曲线是指由美国数学家 Lester Dubins 在20世纪50年代提出的一种特殊类型的最短路径曲线。这种曲线通常用于描述在给定转弯半径下的无人机、汽车或船只等载具的最短路径,其特点是起始点和终点处的切线方向和曲率都是已知的。

Dubins曲线包括直线段和最大转弯半径下的圆弧组成,通过合适的组合可以实现从一个姿态到另一个姿态的最短路径规划。这种曲线在航空、航海、自动驾驶等领域具有广泛的应用,能够有效地规划航行路径,减少能量消耗并提高效率。
2 Dubins曲线原理
2.1 坐标变换
如图所示,在全局坐标系 x O y xOy xOy中,设机器人起始位姿、终止位姿、最小转弯半径分别为 ( x s , y s , α ) \left( x_s,y_s,\alpha \right) (xs,ys,α)、 ( x g , y g , β ) \left( x_g,y_g,\beta \right) (xg,yg,β)与 R R R,则以 p s = ( x s , y s ) \boldsymbol{p}_s=\left( x_s,y_s \right) ps=(xs,ys)为新坐标系原点, p s \boldsymbol{p}_s ps指向 p g = ( x g , y g ) \boldsymbol{p}_g=\left( x_g,y_g \right) pg=(xg,yg)方向为 x ′ x' x′轴,垂直方向为 y ′ y' y′轴建立新坐标系 x ′ O ′ y ′ x'O'y' x′O′y′。
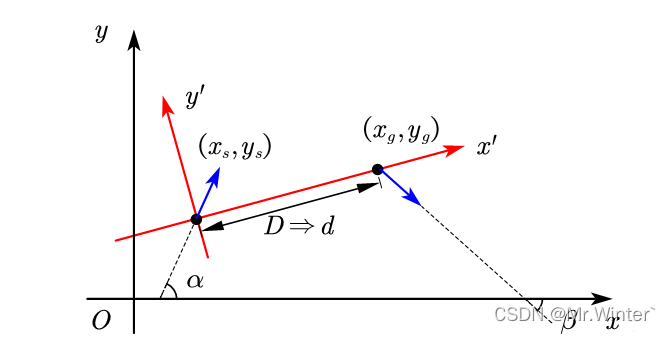
根据比例关系 d / D = r / R {{d}/{D}}={{r}/{R}} d/D=r/R,其中 D = ∥ p s − p g ∥ 2 D=\left\| \boldsymbol{p}_s-\boldsymbol{p}_g \right\| _2 D= ps−pg 2。为了便于后续推导,不妨归一化最小转弯半径,即令 r = 1 r=1 r=1。所以在坐标系 x ′ O ′ y ′ x'O'y' x′O′y′中,通常取起点、终点间距为 d = D / R d={{D}/{R}} d=D/R,从而起始位姿、终止位姿、最小转弯半径分别转换为
s t a r t = [ 0 0 α − θ ] T , g o a l = [ d 0 β − θ ] T , r = 1 \mathrm{start}=\left[ \begin{matrix} 0& 0& \alpha -\theta\\\end{matrix} \right] ^T, \mathrm{goal}=\left[ \begin{matrix} d& 0& \beta -\theta\\\end{matrix} \right] ^T, r=1 start=[00α−θ]T,goal=[d0β−θ]T,r=1
其中 θ = a r c tan ( ( y g − y s ) / ( x g − x s ) ) \theta =\mathrm{arc}\tan \left( {{\left( y_g-y_s \right)}/{\left( x_g-x_s \right)}} \right) θ=arctan((yg−ys)/(xg−xs)),接下来的推导均基于转换坐标系 x ′ O ′ y ′ x'O'y' x′O′y′。
2.2 单步运动公式
对于直行运动,设沿直线行进距离为 l l l,则
[ x ∗ y ∗ ϕ ∗ ] T = [ x + l cos ϕ y + l sin ϕ ϕ ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x+l\cos \phi& y+l\sin \phi& \phi\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x+lcosϕy+lsinϕϕ]T
对于转弯运动,假设转向角为 ψ \psi ψ,则由弧长公式可得
l = ψ r = r = 1 ψ l=\psi r\xlongequal{r=1}\psi l=ψrr=1ψ
因此设沿圆弧行进距离为 l l l,以左转为例,由几何关系易得
[ x ∗ y ∗ ϕ ∗ ] T = [ x + r sin ( ϕ + ψ ) − r sin ( ϕ ) y + r cos ( ϕ + ψ ) + r cos ( ϕ ) ϕ + ψ ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x+r\sin \left( \phi +\psi \right) -r\sin \left( \phi \right)& y+r\cos \left( \phi +\psi \right) +r\cos \left( \phi \right)& \phi +\psi\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x+rsin(ϕ+ψ)−rsin(ϕ)y+rcos(ϕ+ψ)+rcos(ϕ)ϕ+ψ]T
代入 r = 1 r=1 r=1、 ψ = l \psi=l ψ=l可得
[ x ∗ y ∗ ϕ ∗ ] T = [ x + sin ( ϕ + l ) − sin ( ϕ ) y + cos ( ϕ + l ) + cos ( ϕ ) ϕ + l ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x+\sin \left( \phi +l \right) -\sin \left( \phi \right)& y+\cos \left( \phi +l \right) +\cos \left( \phi \right)& \phi +l\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x+sin(ϕ+l)−sin(ϕ)y+cos(ϕ+l)+cos(ϕ)ϕ+l]T
同理,对于右转而言,有
[ x ∗ y ∗ ϕ ∗ ] T = [ x − sin ( ϕ − l ) + sin ( ϕ ) y + cos ( ϕ + l ) − cos ( ϕ ) ϕ − l ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x-\sin \left( \phi -l \right) +\sin \left( \phi \right)& y+\cos \left( \phi +l \right) -\cos \left( \phi \right)& \phi -l\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x−sin(ϕ−l)+sin(ϕ)y+cos(ϕ+l)−cos(ϕ)ϕ−l]T
综上所述,可得单步运动映射
{ L l + ( x , y , ϕ ) = [ x + sin ( ϕ + l ) − sin ( ϕ ) y − cos ( ϕ + l ) + cos ( ϕ ) ϕ + l ] T R l + ( x , y , ϕ ) = [ x − sin ( ϕ − l ) + sin ( ϕ ) y + cos ( ϕ − l ) − cos ( ϕ ) ϕ − l ] T S l + ( x , y , ϕ ) = [ x + l cos ϕ y + l sin ϕ ϕ ] T \begin{cases} L_{l}^{+}\left( x,y,\phi \right) =\left[ \begin{matrix} x+\sin \left( \phi +l \right) -\sin \left( \phi \right)& y-\cos \left( \phi +l \right) +\cos \left( \phi \right)& \phi +l\\\end{matrix} \right] ^T\\ R_{l}^{+}\left( x,y,\phi \right) =\left[ \begin{matrix} x-\sin \left( \phi -l \right) +\sin \left( \phi \right)& y+\cos \left( \phi -l \right) -\cos \left( \phi \right)& \phi -l\\\end{matrix} \right] ^T\\ S_{l}^{+}\left( x,y,\phi \right) =\left[ \begin{matrix} x+l\cos \phi& y+l\sin \phi& \phi\\\end{matrix} \right] ^T\\\end{cases} ⎩ ⎨ ⎧Ll+(x,y,ϕ)=[x+sin(ϕ+l)−sin(ϕ)y−cos(ϕ+l)+cos(ϕ)ϕ+l]TRl+(x,y,ϕ)=[x−sin(ϕ−l)+sin(ϕ)y+cos(ϕ−l)−cos(ϕ)ϕ−l]TSl+(x,y,ϕ)=[x+lcosϕy+lsinϕϕ]T
2.3 曲线模式
Dubins曲线假设物体只能向前,通过组合左转、右转、直行可得六种运动模式
{ L S L , R S R , R S L , L S R , R L R , L R L } \left\{ LSL, RSR, RSL, LSR, RLR, LRL \right\} {LSL,RSR,RSL,LSR,RLR,LRL}
可以总结这六种运动模式的解析解为


3 Dubins曲线生成算法
Dubins曲线路径生成算法流程如表所示

4 仿真实现
4.1 ROS C++实现
核心代码如下所示
Points2d Dubins::generation(Pose2d start, Pose2d goal)
{Points2d path;double sx, sy, syaw;double gx, gy, gyaw;std::tie(sx, sy, syaw) = start;std::tie(gx, gy, gyaw) = goal;// coordinate transformationgx -= sx;gy -= sy;double theta = helper::mod2pi(atan2(gy, gx));double dist = hypot(gx, gy) * max_curv_;double alpha = helper::mod2pi(syaw - theta);double beta = helper::mod2pi(gyaw - theta);// select the best motionDubinsMode best_mode;double best_cost = DUBINS_MAX;DubinsLength length;DubinsLength best_length = { DUBINS_NONE, DUBINS_NONE, DUBINS_NONE };DubinsMode mode;for (const auto solver : dubins_solvers){(this->*solver)(alpha, beta, dist, length, mode);_update(length, mode, best_length, best_mode, best_cost);}if (best_cost == DUBINS_MAX)return path;// interpolation...// coordinate transformationEigen::AngleAxisd r_vec(theta, Eigen::Vector3d(0, 0, 1));Eigen::Matrix3d R = r_vec.toRotationMatrix();Eigen::MatrixXd P = Eigen::MatrixXd::Ones(3, path_x.size());for (size_t i = 0; i < path_x.size(); i++){P(0, i) = path_x[i];P(1, i) = path_y[i];}P = R * P;for (size_t i = 0; i < path_x.size(); i++)path.push_back({ P(0, i) + sx, P(1, i) + sy });return path;
}
4.2 Python实现
核心代码如下所示
def generation(self, start_pose: tuple, goal_pose: tuple):sx, sy, syaw = start_posegx, gy, gyaw = goal_pose# coordinate transformationgx, gy = gx - sx, gy - sytheta = self.mod2pi(math.atan2(gy, gx))dist = math.hypot(gx, gy) * self.max_curvalpha = self.mod2pi(syaw - theta)beta = self.mod2pi(gyaw - theta)# select the best motionplanners = [self.LSL, self.RSR, self.LSR, self.RSL, self.RLR, self.LRL]best_t, best_p, best_q, best_mode, best_cost = None, None, None, None, float("inf")for planner in planners:t, p, q, mode = planner(alpha, beta, dist)if t is None:continuecost = (abs(t) + abs(p) + abs(q))if best_cost > cost:best_t, best_p, best_q, best_mode, best_cost = t, p, q, mode, cost# interpolation...# coordinate transformationrot = Rot.from_euler('z', theta).as_matrix()[0:2, 0:2]converted_xy = rot @ np.stack([x_list, y_list])x_list = converted_xy[0, :] + sxy_list = converted_xy[1, :] + syyaw_list = [self.pi2pi(i_yaw + theta) for i_yaw in yaw_list]return best_cost, best_mode, x_list, y_list, yaw_list
4.3 Matlab实现
核心代码如下所示
function [x_list, y_list, yaw_list] = generation(start_pose, goal_pose, param)sx = start_pose(1); sy = start_pose(2); syaw = start_pose(3);gx = goal_pose(1); gy = goal_pose(2); gyaw = goal_pose(3);% coordinate transformationgx = gx - sx; gy = gy - sy;theta = mod2pi(atan2(gy, gx));dist = hypot(gx, gy) * param.max_curv;alpha = mod2pi(syaw - theta);beta = mod2pi(gyaw - theta);% select the best motionplanners = ["LSL", "RSR", "LSR", "RSL", "RLR", "LRL"];best_cost = inf;best_segs = [];best_mode = [];for i=1:length(planners)planner = str2func(planners(i));[segs, mode] = planner(alpha, beta, dist);if isempty(segs)continueendcost = (abs(segs(1)) + abs(segs(2)) + abs(segs(3)));if best_cost > costbest_segs = segs;best_mode = mode;best_cost = cost;endend% interpolation...% coordinate transformationrot = [cos(theta), -sin(theta); sin(theta), cos(theta)];converted_xy = rot * [x_list; y_list];x_list = converted_xy(1, :) + sx;y_list = converted_xy(2, :) + sy;for j=1:length(yaw_list)yaw_list(j) = pi2pi(yaw_list(j) + theta);end
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

曲线生成 | 图解Dubins曲线生成原理(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 什么是Dubins曲线?2 Dubins曲线原理2.1 坐标变换2.2 单步运动公式2.3 曲线模式 3 Dubins曲线生成算法4 仿真实现4.1 ROS C实现4.2 Python实现4.3 Matlab实现 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、…...

「Vue3系列」Vue3 组件
文章目录 一、Vue3 组件二、Vue3 组件实例三、Vue3 官方组件四、Vue3 常用组件五、相关链接 一、Vue3 组件 Vue3 是 Vue.js 的最新版本,它引入了许多新的特性和改进。在 Vue3 中,组件是构建应用程序的核心部分,它们可以重用、组合和嵌套。Vu…...
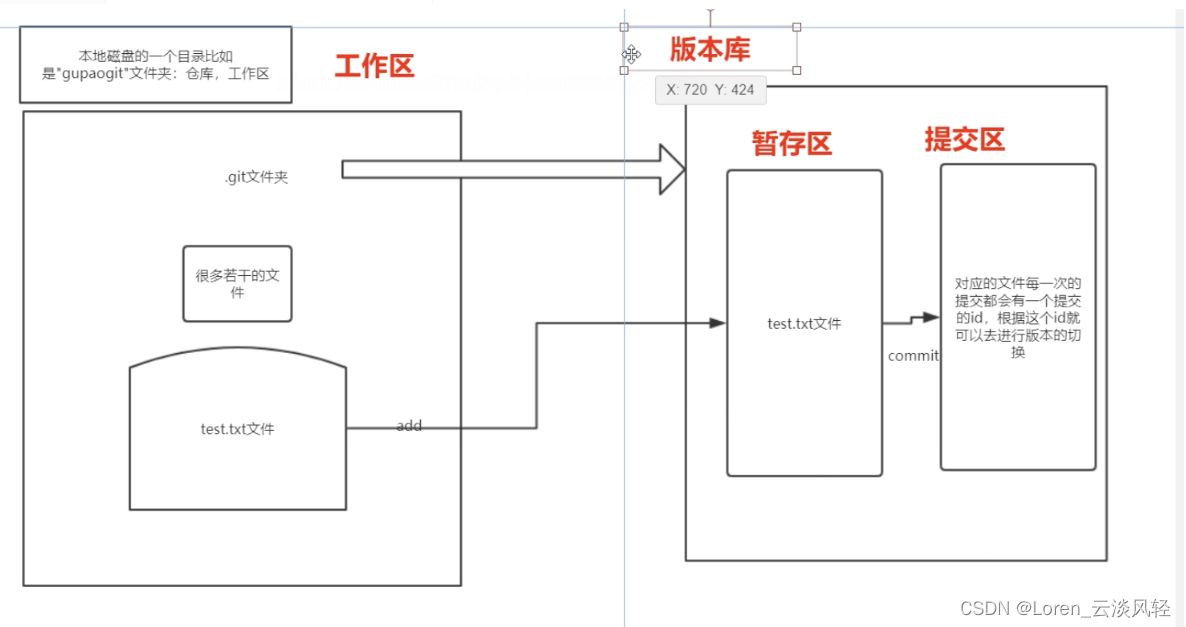
Git实战(2)
git work flow ------------------------------------------------------- ---------------------------------------------------------------- 场景问题及处理 问题1:最近提交了 a,b,c,d记录,想把b记录删掉其他提交记录保留: git reset …...
Java ElasticSearch-Linux面试题
Java ElasticSearch-Linux面试题 前言1、守护线程的作用?2、链路追踪Skywalking用过吗?3、你对G1收集器了解吗?4、你们项目用的什么垃圾收集器?5、内存溢出和内存泄露的区别?6、什么是Spring Cloud Bus?7、…...

微信小程序通过服务器控制ESP8266
声明 本文实现了ESP8266、微信小程序、个人服务器三者互相通信,并且小程序能发消息给微信用户 本文所有代码和步骤均为亲测有效 以下代码均为从网上搜索到后本人加以改动的,并非完全原创,若作者希望删除可联系我 ESP8266与个人服务器通信 ESP8266配置 通过串口通信使用…...

题目 1434: 蓝桥杯历届试题-回文数字
题目描述: 观察数字:12321,123321 都有一个共同的特征,无论从左到右读还是从右向左读,都是相同的。这样的数字叫做:回文数字。 本题要求你找到一些5位或6位的十进制数字。满足如下要求: 该数字的各个数位…...

访问修饰符、Object(方法,使用、equals)、查看equals底层、final--学习JavaEE的day15
day15 一、访问修饰符 含义: 修饰类、方法、属性,定义使用的范围 理解:给类、方法、属性定义访问权限的关键字 注意: 1.修饰类只能使用public和默认的访问权限 2.修饰方法和属性可以使用所有的访问权限 访问修饰符本类本包…...
的性能(来自OpenAI DevDay 会议))
『大模型笔记』最大化大语言模型(LLM)的性能(来自OpenAI DevDay 会议)
最大化大语言模型(LLM)的性能(来自OpenAI DevDay 会议) 文章目录 一. 内容介绍1.1. 优化的两个方向(上下文优化和LLM优化)1.2. 提示工程:从哪里开始1.3. 检索增强生成:拓展知识边界1.4. 微调:专属定制二. 参考文献一. 内容介绍 简述如何以可扩展的方式把大语言模型(LLMs)…...

深度学习:开启你的AI探索之旅
在这个信息爆炸的时代,人工智能(AI)已经渗透到我们生活的方方面面,从智能语音助手到自动驾驶汽车,从智能推荐系统到医疗影像诊断,AI的身影无处不在。而深度学习,作为AI领域的一大核心技术,更是引领着这场科技革命的浪潮。那么,如何入门深度学习,踏上这趟充满挑战与机…...
第十四届蓝桥杯大赛B组 JAVA 蜗牛 (递归剪枝)
题目描述: 这天,一只蜗牛来到了二维坐标系的原点。 在 x 轴上长有 n 根竹竿。它们平行于 y 轴,底部纵坐标为 0,横坐标分别为 x1, x2, …, xn。竹竿的高度均为无限高,宽度可忽略。蜗牛想要从原点走到第 n 个竹竿的底部也…...

基于React低代码平台开发:构建高效、灵活的应用新范式
文章目录 一、React与低代码平台的结合优势二、基于React的低代码平台开发挑战三、基于React的低代码平台开发实践四、未来展望《低代码平台开发实践:基于React》编辑推荐内容简介作者简介目录前言为什么要写这本书 读者对象如何阅读本书 随着数字化转型的深入&…...
)
在Linux部署Docker并上传静态资源(快速教程)
Nginx快速上手 安装必要的软件包 yum install -y yum-utils device-mapper-persistent-data lvm2设置Docker仓库 通过以下命令添加Docker的官方仓库到yum源中: yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo安装Dock…...

【场景测试用例】带有广告图案的纸杯
从以下几个纬度出发考虑: 功能 是否可以承载液体,热水,温水,冰水是否可以承载非液体类的物品容量,空杯,半杯,满杯 UI 广告图案设计是否合理 性能 最大承受的容量内不漏水(负载测试)最大承受的温…...
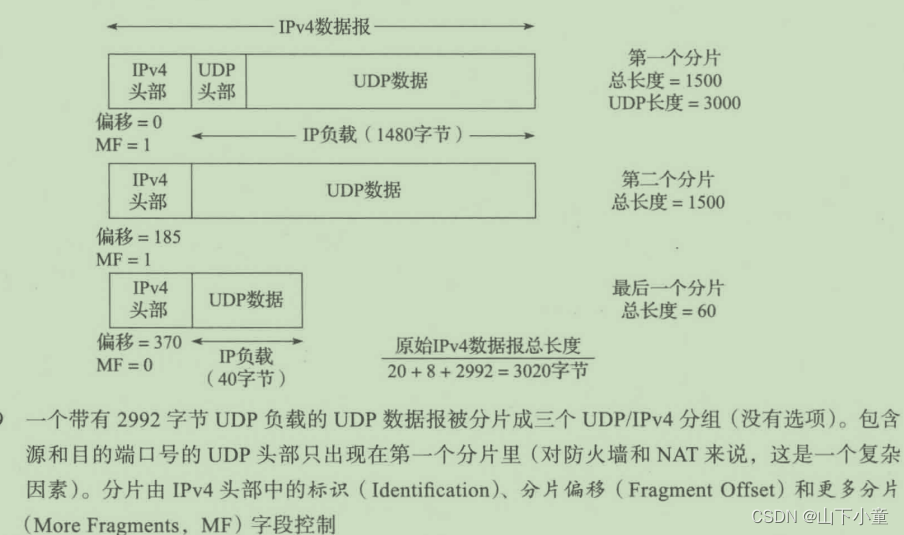
《TCP/IP详解 卷一》第10章 UDP 和 IP 分片
目录 10.1 引言 10.2 UDP 头部 10.3 UDP校验和 10.4 例子 10.5 UDP 和 IPv6 10.6 UDP-Lite 10.7 IP分片 10.7.1 例子:IPV4 UDP分片 10.7.2 重组超时 10.8 采用UDP的路径MTU发现 10.9 IP分片和ARP/ND之间的交互 10.10 最大UDP数据报长度 10.11 UDP服务器…...
MyBatisPlus(SpringBoot版)的分页插件
目录 一、前置工作: 1.整体项目目录结构 2.创建普通javamaven项目。 3.导入依赖,改造成springboot项目 4.配置启动类 5.创建service接口及其实现类 6.创建接口Mapper 7.配置数据源 8.创建数据库表 二、使用MP(mybatisplus)的分页插件 二、使…...
【小沐学QT】QT学习之信号槽使用
文章目录 1、简介2、代码实现2.1 界面菜单“转到槽”方法2.2 界面信号槽编辑器方法2.3 QT4.0的绑定方法2.4 QT5.0之后的绑定方法2.5 C11的方法2.6 lamda表达式方法2.7 QSignalMapper方法 结语 1、简介 在GUI编程中,当我们更改一个小部件时,我们通常希望…...

SpringMVC总结
SpringMVC SpringMVC是隶属于Spring框架的一部分,主要是用来进行Web开发,是对Servlet进行了封装。 对于SpringMVC我们主要学习如下内容: SpringMVC简介 请求与响应 REST风格 SSM整合(注解版) 拦截器 SpringMVC是处理Web层/表现层的框架ÿ…...

JS一些重要函数
防抖函数 避免短时间内的函数多次调用影响性能 function debounce(func , wait){let timer;return (...args) > {clearTimeout(timer);timer setTimeout(() > {return func(args)} , wait)} } 函数柯里化 将多参函数以单参的形式传递 function curry(fn){return func…...

基于视觉识别的自动采摘机器人设计与实现
一、前言 1.1 项目介绍 【1】项目功能介绍 随着科技的进步和农业现代化的发展,农业生产效率与质量的提升成为重要的研究对象。其中,果蔬采摘环节在很大程度上影响着整个产业链的效益。传统的手工采摘方式不仅劳动强度大、效率低下,而且在劳…...

算法D32 | 贪心算法2 | 122.买卖股票的最佳时机II 55. 跳跃游戏 45.跳跃游戏II
122.买卖股票的最佳时机II 本题解法很巧妙,大家可以看题思考一下,在看题解。 代码随想录P 只收集每天的正利润,利润可以每天分解。 Python: class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices)<2: retur…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
