经典的算法面试题(1)
题目:
给定一个整数数组 nums,编写一个算法将所有的0移到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
注意:必须在原数组上操作,不能拷贝额外的数组。尽量减少操作次数。
这个问题考察候选人处理数组的能力,以及他们编写高效、优雅代码的能力。在解决问题时,请考虑如何避免不必要的元素移动。
思路:
1、双指针法:
使用两个指针,一个用来遍历数组(遍历指针),另一个指向最新发现的非零元素应当存放的位置(非零指针)。
当遍历指针指向的值不为0时,将其与非零指针指向的值交换,然后非零指针前移。
通过整个数组的遍历,所有非零元素都被推向数组的开头,而0都被留在了数组的末尾。
2、计数零元素法:
首先遍历一次数组,统计出0的个数。
在第二次遍历期间,使用一个新的索引(比如 insertPos),它基于0的计数从数组开头开始移动。
如果遍历到非零元素,就将它放到insertPos的位置,并将insertPos向前移动。
遍历完成后,按照统计出的0的个数,在数组末尾补上0。
3、移动非零元素法:
遍历数组,一旦遇到非0数,就将其移到数组最前方现有非0数的后面。
记录最后一个非0数的位置。
在数组剩余的部分填充0。
每种方法都有其特点,但双指针法在空间和操作复杂度上通常是最优的。这个方法只需要( O(n) )的时间复杂度和( O(1) )的额外空间复杂度。
时间复杂度
1. **双指针法**:时间复杂度为 ( O(n) ),因为只需要遍历一遍数组,n 为数组长度。
2. **计数零元素法**:时间复杂度为 ( O(n) ),即便需要两次遍历(一次计数0的个数,一次移动非零元素),但两次遍历的时间复杂度都是线性的。
3. **移动非零元素法**:时间复杂度也为 ( O(n) ),一次线性遍历即可完成所有非零元素的移动和0的填充。
值得注意的是,尽管所有方法的时间复杂度都是线性的,但实际执行时间可能会因为常数因子和元素实际移动次数的差异而有所不同。在决定使用哪一种方法时,这也是需要考虑的因素之一。
实现代码
1、双指针法
#include <stdio.h>
void moveZeroes(int* nums, int numsSize) {int j = 0; // 指向当前非0元素应该插入的位置for (int i = 0; i < numsSize; ++i) {if (nums[i] != 0) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;j++;}}
}2、计数零元素法:
#include <stdio.h>
void moveZeroes(int* nums, int numsSize) {int zeroCount = 0; // 计算数组中0的个数for (int i = 0; i < numsSize; i++) {if (nums[i] == 0) {zeroCount++;}}int index = 0;for (int i = 0; i < numsSize; i++) {if (nums[i] != 0) {nums[index++] = nums[i];}}for (int i = index; i < numsSize; i++) {nums[i] = 0;}
}3、移动非零元素法:
#include <stdio.h>
void moveZeroes(int* nums, int numsSize) {int insertPos = 0; // 指向当前已处理数组的末尾for (int i = 0; i < numsSize; i++) {if (nums[i] != 0) {nums[insertPos++] = nums[i];}}while (insertPos < numsSize) {nums[insertPos++] = 0;}
}相关文章:

经典的算法面试题(1)
题目: 给定一个整数数组 nums,编写一个算法将所有的0移到数组的末尾,同时保持非零元素的相对顺序。 示例: 输入: [0,1,0,3,12] 输出: [1,3,12,0,0] 注意:必须在原数组上操作,不能拷贝额外的数组。尽量减少操作次数。 这…...

微信小程序 --- mobx-miniprogram miniprogram-computed
1.1 mobx-miniprogram 介绍 目前已经学习了 6 种小程序页面、组件间的数据通信方案,分别是: 数据绑定:properties获取组件实例:this.selectComponent()事件绑定:this.triggerEvent()获取应用实例:getApp(…...
【HTML】HTML基础2(一些常用标签)
目录 例子 首先是网页图标 然后是一些常用标签 插入图片 例子 <!DOCTYPE html> <html><head><link rel"icon" href"img/银河护卫队-星爵.png" type"image/x-icon"><meta charset"utf-8"><title>…...
Jmeter 安装
JMeter是Java的框架,因此在安装Jmeter前需要先安装JDK,此处安装以Windows版为例 1. 安装jdk:Java Downloads | Oracle 安装完成后设置环境变量 将环境变量JAVA_HOME设置为 C:\Program Files\Java\jdk1.7.0_25 在系统变量Path中添加 C:\Pro…...

控制液压比例插装阀放大器
比例阀放大器接收来自控制器的低功率电信号,并将其转换为足以驱动比例阀的高功率信号。与传统的开关型电磁铁不同,比例电磁铁可以实现连续控制,允许阀门在开和关之间进行无级调节,从而实现更精细的流量和压力控制。一个完整的电液…...
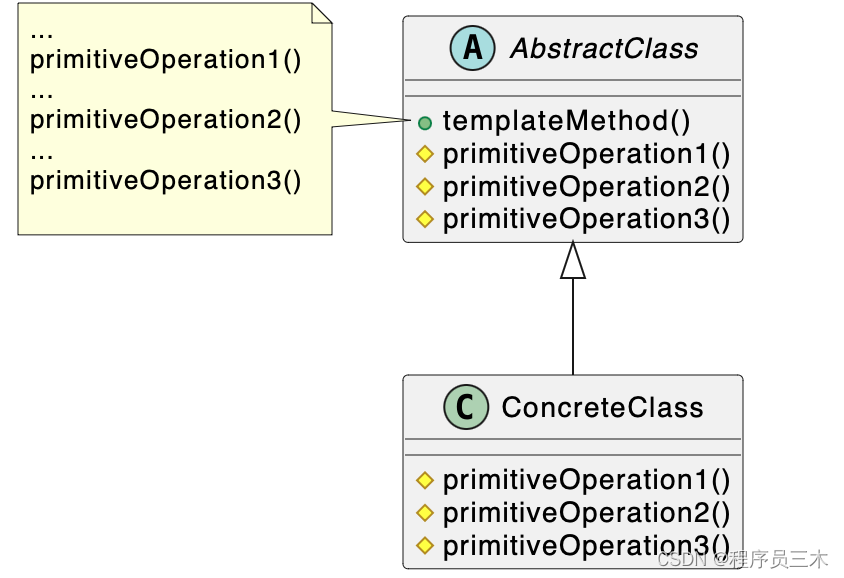
[设计模式Java实现附plantuml源码~行为型]定义算法的框架——模板方法模式
前言: 为什么之前写过Golang 版的设计模式,还在重新写Java 版? 答:因为对于我而言,当然也希望对正在学习的大伙有帮助。Java作为一门纯面向对象的语言,更适合用于学习设计模式。 为什么类图要附上uml 因为很…...

nftables 测试一拒绝所有流量
要配置 nftables 先拒绝所有流量,然后再添加允许的规则,您可以按照以下步骤操作: 创建一个空的 nftables 配置文件(例如 /etc/nftables.conf)并添加如下内容: flush rulesettable inet filter {chain input…...

练习 3 Web [ACTF2020 新生赛]Upload
[ACTF2020 新生赛]Upload1 中间有上传文件的地方,试一下一句话木马 txt 不让传txt 另存为tlyjpg,木马文件上传成功 给出了存放目录: Upload Success! Look here~ ./uplo4d/06a9d80f64fded1e542a95e6d530c70a.jpg 下一步尝试改木马文件后缀…...

Linux中docker项目提示No such file or directory
本来以为是文件权限问题,后来发现是个非常蠢的问题 文件没有映射到容器中 docker文件映射语法 Docker 使用 -v 或 --volume 参数来指定文件映射。 增加在运行命令后 -v <宿主机目录>:<容器目录> 其中,宿主机目录 是指要映射的宿主机上的…...

PyTorch 中的 apply
Abstract nn.Module[List].apply(callable)Tensor.apply_(callable) → TensorFunction.apply(Tensor...) nn.Module[List].apply()? 源码: def apply(self: T, fn: Callable[[Module], None]) -> T:"""Typical use includes initializing the paramete…...
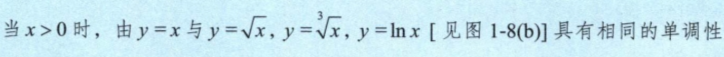
张宇30讲学习笔记
初等数学 x \sqrt{x} x 是算数平方根,一定≥0; x 2 \sqrt{x^2} x2 |x| x2|x2||x|2 x3≠|x3||x|3 不等式 a>0,b>0,则ab≥2 a b \sqrt{ab} ab 对数 ln a b \frac{a}{b} balna-lnb 高等数学 单调性 线性代数...
SpringBoot接口防抖(防重复提交)的一些实现方案
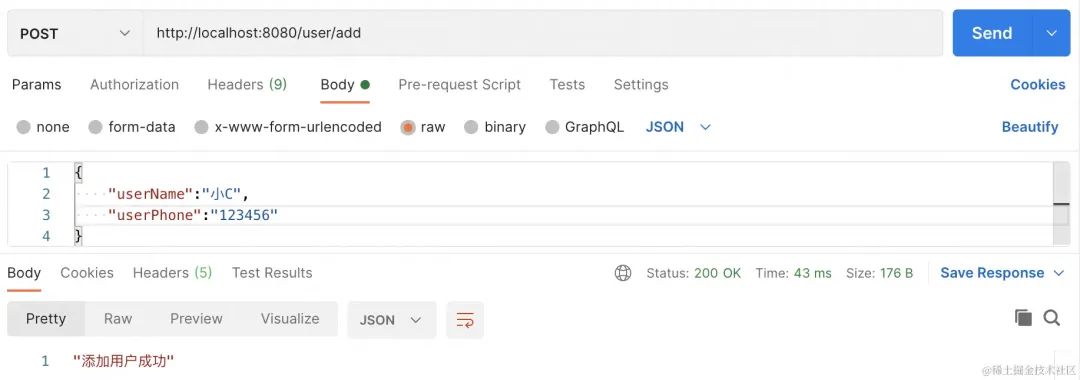
前言 啥是防抖 思路解析 分布式部署下如何做接口防抖? 具体实现 请求锁 唯一key生成 重复提交判断 前言 作为一名老码农,在开发后端Java业务系统,包括各种管理后台和小程序等。在这些项目中,我设计过单/多租户体系系统&a…...

Qt/C++音视频开发67-保存裸流加入sps/pps信息/支持264/265裸流/转码保存/拉流推流
一、前言 音视频组件除了支持保存MP4文件外,同时还支持保存裸流即264/265文件,以及解码后最原始的yuv文件。在实际使用过程中,会发现部分视频文件保存的裸流文件,并不能直接用播放器播放,查阅资料得知原来是缺少sps/p…...

【Web】速谈FastJson反序列化中TemplatesImpl的利用
目录 简要原理分析 exp 前文:【Web】关于FastJson反序列化开始前的那些前置知识 简要原理分析 众所周知TemplatesImpl的利用链是这样的: TemplatesImpl#getOutputProperties() -> TemplatesImpl#newTransformer() -> TemplatesImpl#getTransl…...

RK3568 RK809电源管理 RTC功能使能 定时唤醒
概述 RK809 是一款高性能 PMIC,RK809 集成 5 个大电流 DCDC、9 个 LDO、2 个 开关SWITCH、 1个 RTC、1个 高性能CODEC、可调上电时序等功能。 系统中各路电源总体分为两种:DCDC 和 LDO。两种电源的总体特性如下(详细资料请自行搜索): DCDC:输入输出压差大时,效率高,但…...
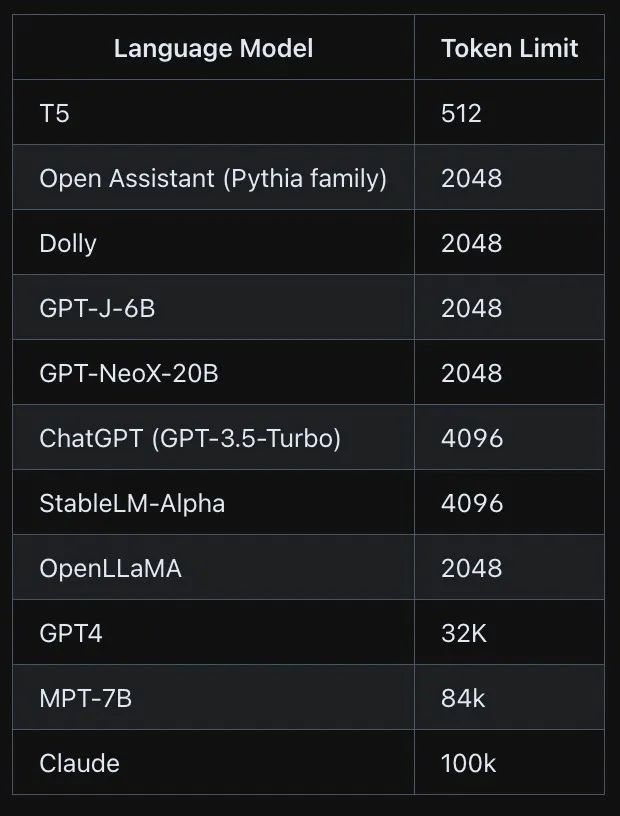
大模型(LLM)的token学习记录-I
文章目录 基本概念什么是token?如何理解token的长度?使用openai tokenizer 观察token的相关信息open ai的模型 token的特点token如何映射到数值?token级操作:精确地操作文本token 设计的局限性 tokenizationtoken 数量对LLM 的影响训练模型参…...
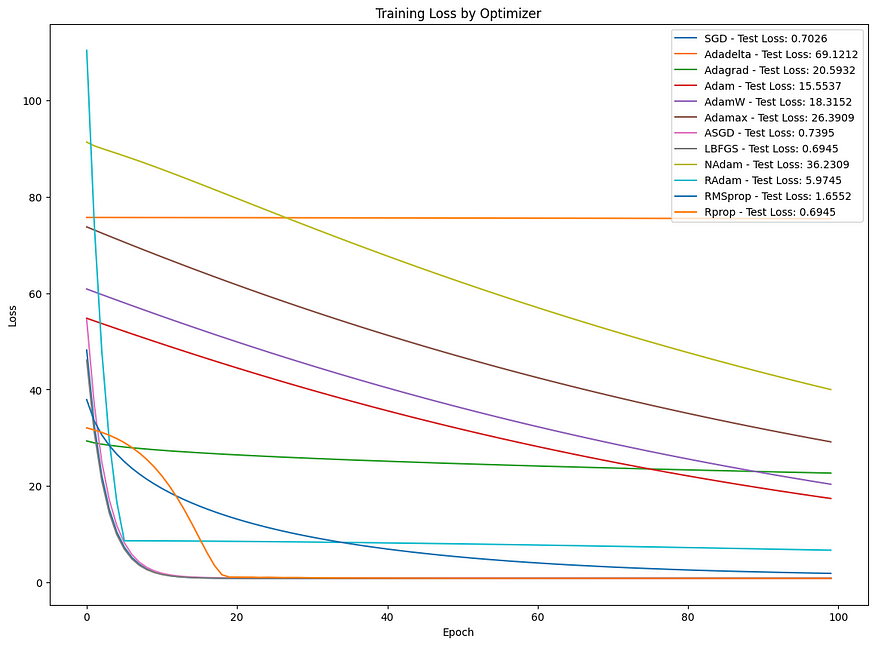
探索前景:机器学习中常见优化算法的比较分析
目录 一、介绍 二、技术背景 三、相关代码 四、结论 一、介绍 优化算法在机器学习和深度学习中至关重要,可以最小化损失函数,从而改善模型的预测。每个优化器都有其独特的方法来导航损失函数的复杂环境以找到最小值。本文探讨了一些最常见的优化算法&…...

基于MRI的阿尔兹海默症病情预测
《阿尔兹海默症病情预测系统:老年痴呆患者的福音》 引言项目背景和意义数据介绍与分析模型介绍模型训练与评估模型应用与展望 引言 阿尔兹海默症(Alzheimer’s Disease)是一种常见的老年疾病,给患者及其家庭带来了巨大的困扰和负…...

高维中介数据: 联合显着性(JS)检验法
摘要 中介分析在流行病学和临床试验中越来越受到关注。在现有的中介分析方法中,流行的联合显着性(JS)检验会产生过于保守的 I 类错误率,因此功效较低。但是,如果在使用 JS 测试高维中介假设时,可以准确控制…...

冒泡排序 和 qsort排序
目录 冒泡排序 冒泡排序部分 输出函数部分 主函数部分 总代码 控制台输出显示 总代码解释 冒泡排序优化 冒泡排序 主函数 总代码 代码优化解释 qsort 排序 qsort 的介绍 使用qsort排序整型数据 使用qsort排序结构数据 冒泡排序 首先,我先介绍我的冒泡…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
