292.【华为OD机试】跳马问题(广度优先搜索(BFS)JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~
本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握!文章目录
- 一. 题目
- 二.解题思路
- 三.题解代码
- Python题解代码
- JAVA题解代码
- C/C++题解代码
- JS题解代码
- 四.代码讲解(Java&Python&C++&JS分别讲解)
相关文章:
JavaPythonC++JS实现))
292.【华为OD机试】跳马问题(广度优先搜索(BFS)JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目二.解题思路三.题解代码Python题解代码JAVA题解…...

Qt 中Qwidget相关属性
文章目录 1. QWidget 核心属性1.1 enabled1.2 geometry1.2.1 window frame 的影响 1.3 windowTitle1.4 windowIcon1.4.1 qrc的使用 1.5 windowOpacity1.6 cursor1.7 focusPolicy1.8 styleSheet 1. QWidget 核心属性 在 Qt 中, 使⽤ QWidget 类表⽰ “控件”. 像按钮, 视图, 输…...
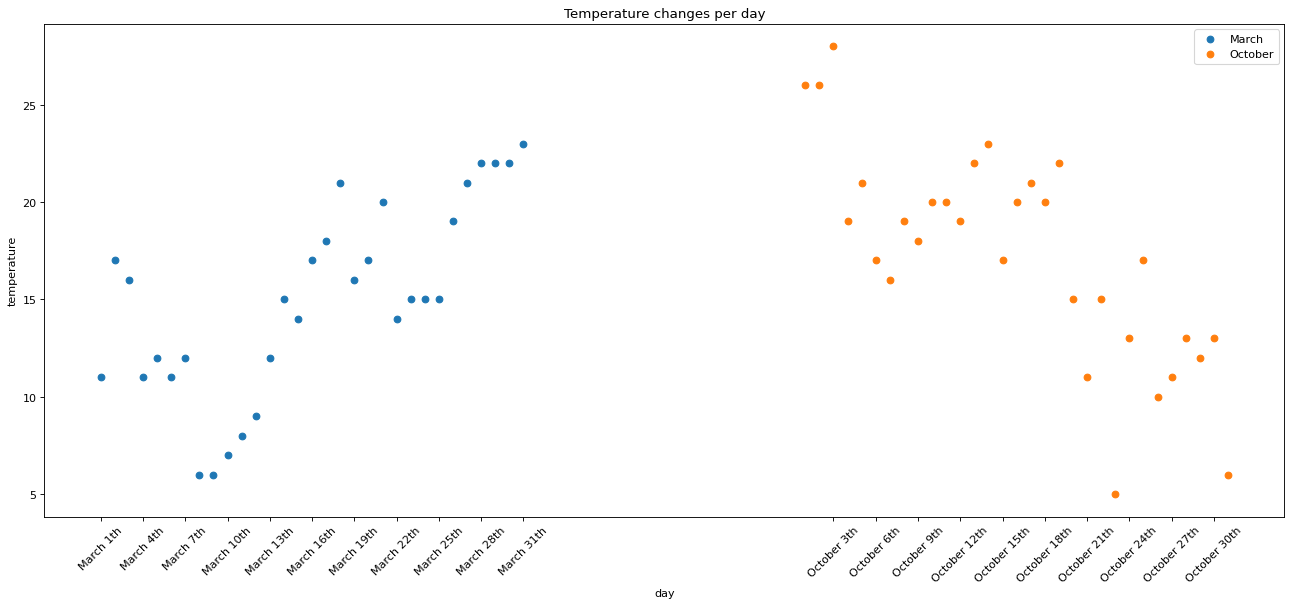
matplotlib散点图
matplotlib散点图 假设通过爬虫你获取到了北京2016年3, 10月份每天白天的最高气温(分别位于列表a, b), 那么此时如何寻找出气温和随时间(天)变化的某种规律? from matplotlib import pyplot as pltx_3 range(1, 32) x_10 range(51, 82)y_3 [11,17,16,11,12,11,12,6,6,7,8…...
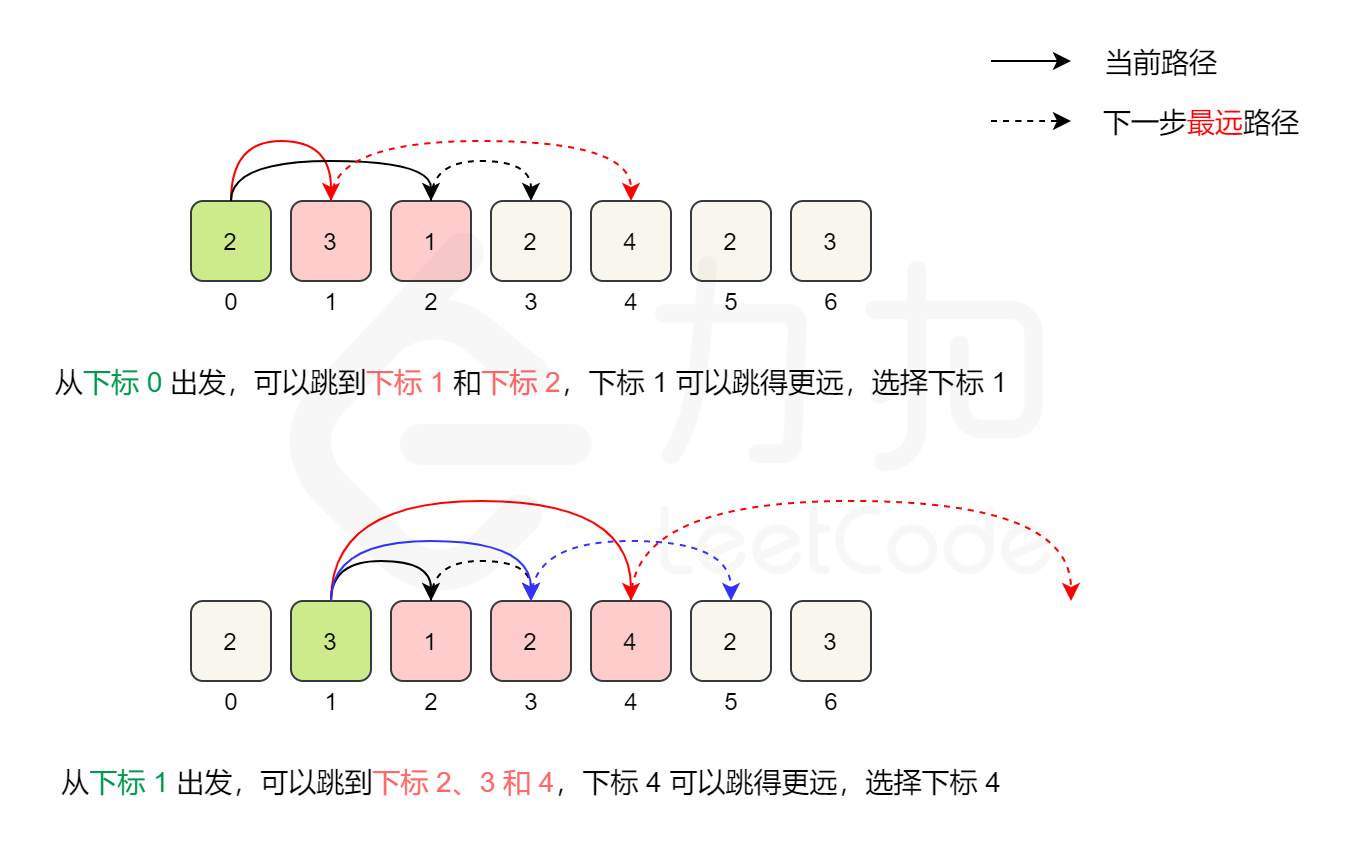
day32贪心算法 part02
贪心系列的时候,题目和题目之间貌似没有什么联系,是真的就是没什么联系,因为贪心无套路,没有个整体的贪心框架解决一系列问题,只能是接触各种类型的题目锻炼自己的贪心思维。贪心只是一类题的统称,并没有什么固定套路。 122. 买卖…...

判断docker 镜像启动成功 shell脚本
要编写一个Shell脚本来判断Docker镜像是否启动成功,你可以使用docker ps命令来检查容器是否在运行状态。以下是一个简单的Shell脚本示例,用于判断Docker镜像是否成功启动: #!/bin/bash# 指定要检查的容器名称或ID CONTAINER_NAME"your_c…...

Android AppCompatActivity 方法详解
在 Android 开发中,AppCompatActivity 是一个常用的类,它提供了对新版 Android 特性在旧版 Android 上的兼容支持。作为 Android 支持库的一部分,它通常被用作活动(Activity)的基类。下面我们将介绍 AppCompatActivity…...

[FastDDS] 基于eProsima FastDDS的移动机器人数据中间件——介绍与准备工作
[FastDDS] 基于eProsima FastDDS的移动机器人数据中间件——介绍与准备工作 注明:无 本栏目主要讲述,基于eProsima FastDDS的移动机器人数据中间件的实现、使用、性能测试。 What is [ FastDDS ]: eProsima Fast DDS是DDS(数据分发服务&…...
4. 编写app组件
1. 代码 main.ts // 引入createApp用于创建应用 import {createApp} from "vue"// 引入App根组件 import App from ./App.vue createApp(App).mount(#app) App.vue <!-- vue文件可以写三种标签1. template标签,写html结构2. script 脚本标签&…...

经典的算法面试题(1)
题目: 给定一个整数数组 nums,编写一个算法将所有的0移到数组的末尾,同时保持非零元素的相对顺序。 示例: 输入: [0,1,0,3,12] 输出: [1,3,12,0,0] 注意:必须在原数组上操作,不能拷贝额外的数组。尽量减少操作次数。 这…...

微信小程序 --- mobx-miniprogram miniprogram-computed
1.1 mobx-miniprogram 介绍 目前已经学习了 6 种小程序页面、组件间的数据通信方案,分别是: 数据绑定:properties获取组件实例:this.selectComponent()事件绑定:this.triggerEvent()获取应用实例:getApp(…...
【HTML】HTML基础2(一些常用标签)
目录 例子 首先是网页图标 然后是一些常用标签 插入图片 例子 <!DOCTYPE html> <html><head><link rel"icon" href"img/银河护卫队-星爵.png" type"image/x-icon"><meta charset"utf-8"><title>…...
Jmeter 安装
JMeter是Java的框架,因此在安装Jmeter前需要先安装JDK,此处安装以Windows版为例 1. 安装jdk:Java Downloads | Oracle 安装完成后设置环境变量 将环境变量JAVA_HOME设置为 C:\Program Files\Java\jdk1.7.0_25 在系统变量Path中添加 C:\Pro…...

控制液压比例插装阀放大器
比例阀放大器接收来自控制器的低功率电信号,并将其转换为足以驱动比例阀的高功率信号。与传统的开关型电磁铁不同,比例电磁铁可以实现连续控制,允许阀门在开和关之间进行无级调节,从而实现更精细的流量和压力控制。一个完整的电液…...
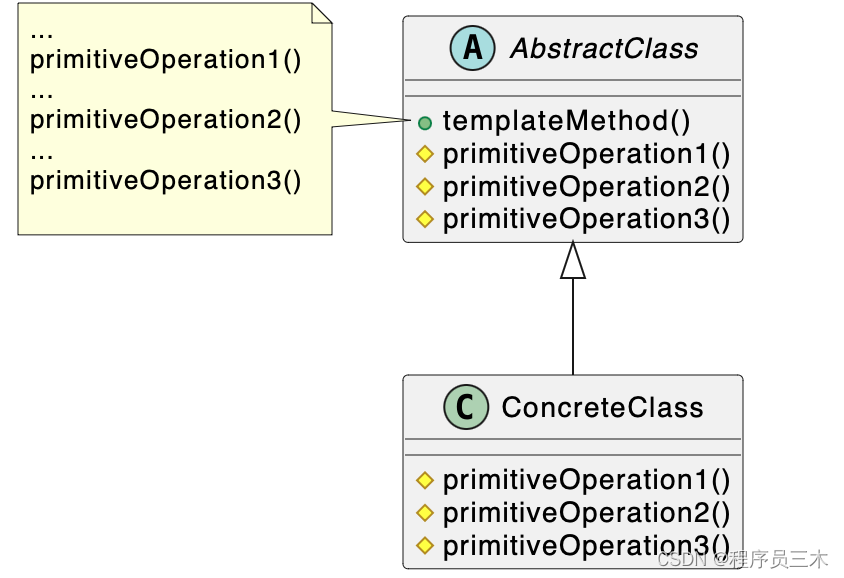
[设计模式Java实现附plantuml源码~行为型]定义算法的框架——模板方法模式
前言: 为什么之前写过Golang 版的设计模式,还在重新写Java 版? 答:因为对于我而言,当然也希望对正在学习的大伙有帮助。Java作为一门纯面向对象的语言,更适合用于学习设计模式。 为什么类图要附上uml 因为很…...

nftables 测试一拒绝所有流量
要配置 nftables 先拒绝所有流量,然后再添加允许的规则,您可以按照以下步骤操作: 创建一个空的 nftables 配置文件(例如 /etc/nftables.conf)并添加如下内容: flush rulesettable inet filter {chain input…...

练习 3 Web [ACTF2020 新生赛]Upload
[ACTF2020 新生赛]Upload1 中间有上传文件的地方,试一下一句话木马 txt 不让传txt 另存为tlyjpg,木马文件上传成功 给出了存放目录: Upload Success! Look here~ ./uplo4d/06a9d80f64fded1e542a95e6d530c70a.jpg 下一步尝试改木马文件后缀…...

Linux中docker项目提示No such file or directory
本来以为是文件权限问题,后来发现是个非常蠢的问题 文件没有映射到容器中 docker文件映射语法 Docker 使用 -v 或 --volume 参数来指定文件映射。 增加在运行命令后 -v <宿主机目录>:<容器目录> 其中,宿主机目录 是指要映射的宿主机上的…...

PyTorch 中的 apply
Abstract nn.Module[List].apply(callable)Tensor.apply_(callable) → TensorFunction.apply(Tensor...) nn.Module[List].apply()? 源码: def apply(self: T, fn: Callable[[Module], None]) -> T:"""Typical use includes initializing the paramete…...
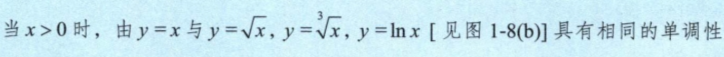
张宇30讲学习笔记
初等数学 x \sqrt{x} x 是算数平方根,一定≥0; x 2 \sqrt{x^2} x2 |x| x2|x2||x|2 x3≠|x3||x|3 不等式 a>0,b>0,则ab≥2 a b \sqrt{ab} ab 对数 ln a b \frac{a}{b} balna-lnb 高等数学 单调性 线性代数...
SpringBoot接口防抖(防重复提交)的一些实现方案
前言 啥是防抖 思路解析 分布式部署下如何做接口防抖? 具体实现 请求锁 唯一key生成 重复提交判断 前言 作为一名老码农,在开发后端Java业务系统,包括各种管理后台和小程序等。在这些项目中,我设计过单/多租户体系系统&a…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
