LeetCode每日一题【c++版】- 用队列实现栈与用栈实现队列
用队列实现栈
题目描述
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false] 解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False
解题思路
栈是一种后进先出的数据结构,元素从顶端入栈,然后从顶端出栈。
队列是一种先进先出的数据结构,元素从后端入队,然后从前端出队。
为了满足栈的特性,即最后入栈的元素最先出栈,在使用队列实现栈时,应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作,其中queue1用于存储栈内的元素,queue2作为入栈操作的辅助队列。
入栈操作时,首先将元素入队到 queue2,然后将 queue1的全部元素依次出队并入队到 queue2,此时 queue2的前端的元素即为新入栈的元素,再将 queue1和 queue2互换,则 queue1的元素即为栈内的元素,queue1的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保 queue1的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除 queue1的前端元素并返回即可,获得栈顶元素操作只需要获得 queue1的前端元素并返回即可(不移除元素)。
由于 queue1用于存储栈内的元素,判断栈是否为空时,只需要判断 queue1是否为空即可。
复杂度分析
时间复杂度:入栈操作O(n),其余操作都是O(1),n是栈内的元素个数
空间复杂度:O(n),需要使用两个队列存储站内的元素
代码
#include <queue>
#include <array>
#include <iostream>
using namespace std;
class MyStack
{
public:queue<int> queue1;queue<int> queue2;/** 初始化栈. */MyStack(){}/** 向栈内添加元素. */void push(int x){queue2.push(x);while (!queue1.empty()){queue2.push(queue1.front());queue1.pop();}swap(queue1, queue2);}/** 移除栈顶元素 */int pop(){int r = queue1.front();queue1.pop();return r;}/** 返回栈顶元素. */int top(){int r = queue1.front();return r;}/** 返回栈是否为空. */bool empty(){return queue1.empty();}
};
int main()
{MyStack myStack;myStack.push(1);myStack.push(2);cout << myStack.top() << endl; // 返回 2cout << myStack.pop() << endl;; // 返回 2cout << myStack.empty() << endl; // 返回 False
}用栈实现队列
题目描述
链接:简单232.用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾代码int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
解题思路
将一个栈当作输入栈,用于压入 push传入的数据;另一个栈当作输出栈,用于 pop和 peek操作。每次 pop或 peek时,若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。
复杂度分析
时间复杂度:push和 emptyO(1),pop和 peek为均摊 O(1)。对于每个元素,至多入栈和出栈各两次,故均摊复杂度为 O(1)。
空间复杂度:O(n)。其中 n是操作总数。对于有 n次 push操作的情况,队列中会有 n个元素,故空间复杂度为 O(n)。
代码
#include <stack>
#include <iostream>
using namespace std;
class MyQueue
{
public:MyQueue(){}void push(int x){// 1.把s1所有元素弹出后依次放入s2while (!s1.empty()){s2.push(s1.top());s1.pop();}// 2.新元素加入到s2顶部s2.push(x);// 3.把s2所有元素弹出后依次放入s1while (!s2.empty()){s1.push(s2.top());s2.pop();}}int pop(){int ret = s1.top();s1.pop();return ret;}int peek(){return s1.top();}bool empty(){return s1.empty();}private:stack<int> s1;stack<int> s2;
};
int main()
{MyQueue myQueue;myQueue.push(1); // queue is: [1]myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)cout << myQueue.peek() << endl; // return 1cout << myQueue.pop() << endl; // return 1, queue is [2]cout << myQueue.empty() <<endl; // return false
}相关文章:

LeetCode每日一题【c++版】- 用队列实现栈与用栈实现队列
用队列实现栈 题目描述 请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。 实现 MyStack 类: void push(int x) 将元素 x 压入栈顶。int pop() 移除…...

深入理解快速排序算法:从原理到实现
目录 1. 引言 2. 快速排序算法原理 3. 快速排序的时间复杂度分析 4. 快速排序的应用场景 5. 快速排序的优缺点分析 5.1 优点: 5.2 缺点: 6. Java、JavaScript 和 Python 实现快速排序算法 6.1 Java 实现: 6.2 JavaScript 实现&#…...
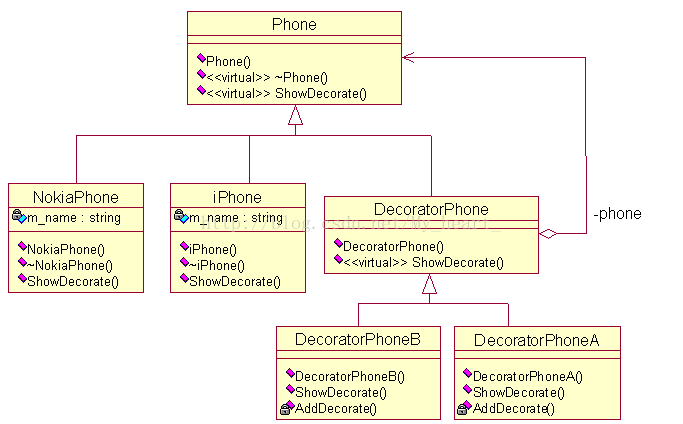
设计模式----装饰器模式
在软件开发过程中,有时想用一些现存的组件。这些组件可能只是完成了一些核心功能。但在不改变其结构的情况下,可以动态地扩展其功能。所有这些都可以釆用装饰器模式来实现。 装饰器模式 允许向一个现有的对象添加新的功能,同时又不改变他的…...
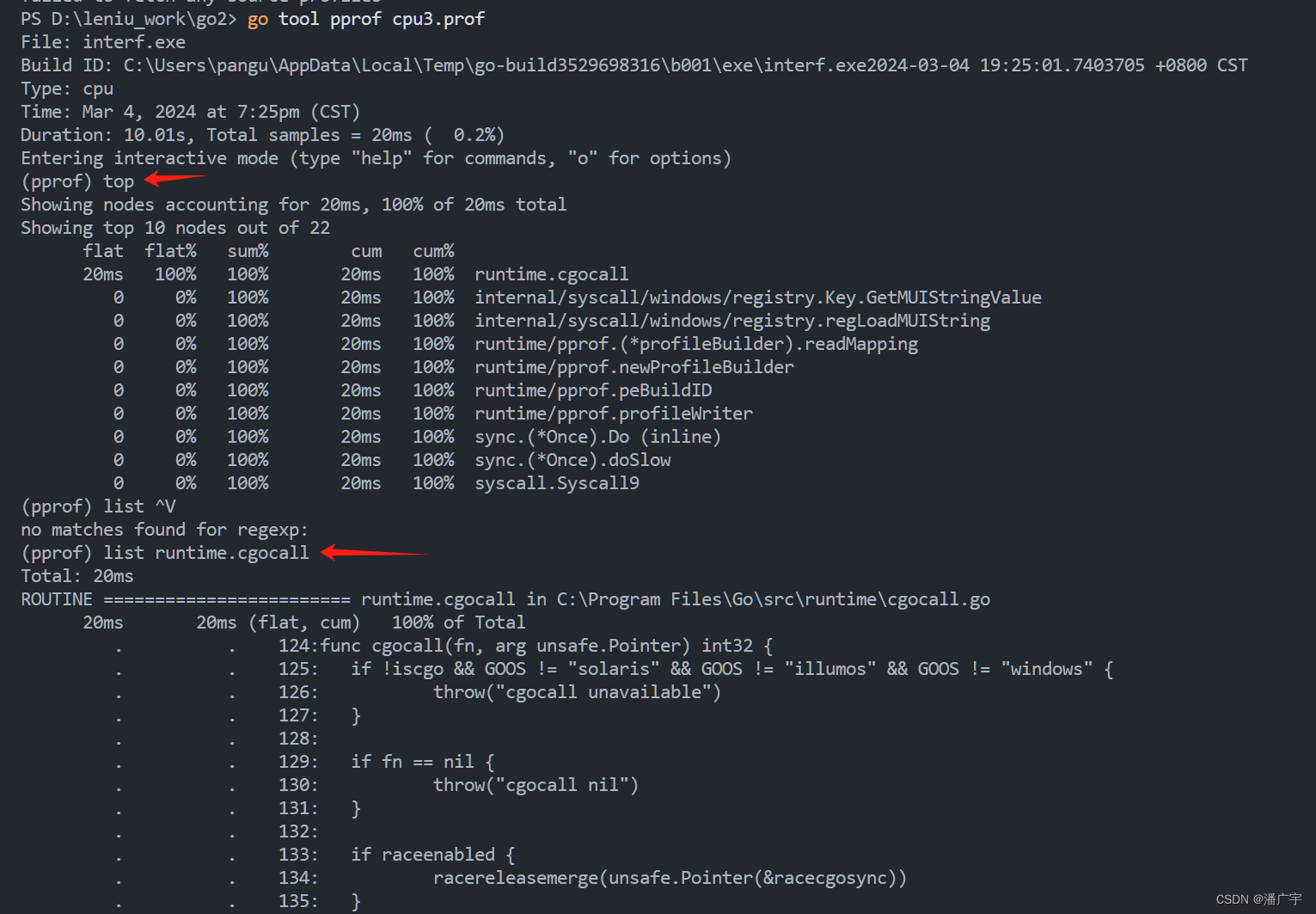
Golang pprof 分析程序的使用内存和执行时间
一、分析程序执行的内存情况 package mainimport ("os""runtime/pprof" )func main() {// ... 你的程序逻辑 ...// 将 HeapProfile 写入文件f, err : os.Create("heap.prof")if err ! nil {panic(err)}defer f.Close()pprof.WriteHeapProfile(f…...
C/C++平方和问题(蓝桥杯)
题目描述: 小明对数位中含有2、0、1、9 的数字很感兴趣,在1 到40 中这样的数包 括1、2、9、10 至32、39 和40,共28 个,他们的和是574,平方和是14362。 注意,平方和是指将每个数分别平方后求和。 请问&#…...

(libusb) usb口自动刷新
文章目录 libusb自动刷新程序Code目录结构Code项目文件usb包code包 效果描述重置reset热拔插使用 END libusb 在操作USB相关内容时,有一个比较著名的库就是libusb。 官方网址:libusb 下载: 下载源码官方编好的库github:Release…...
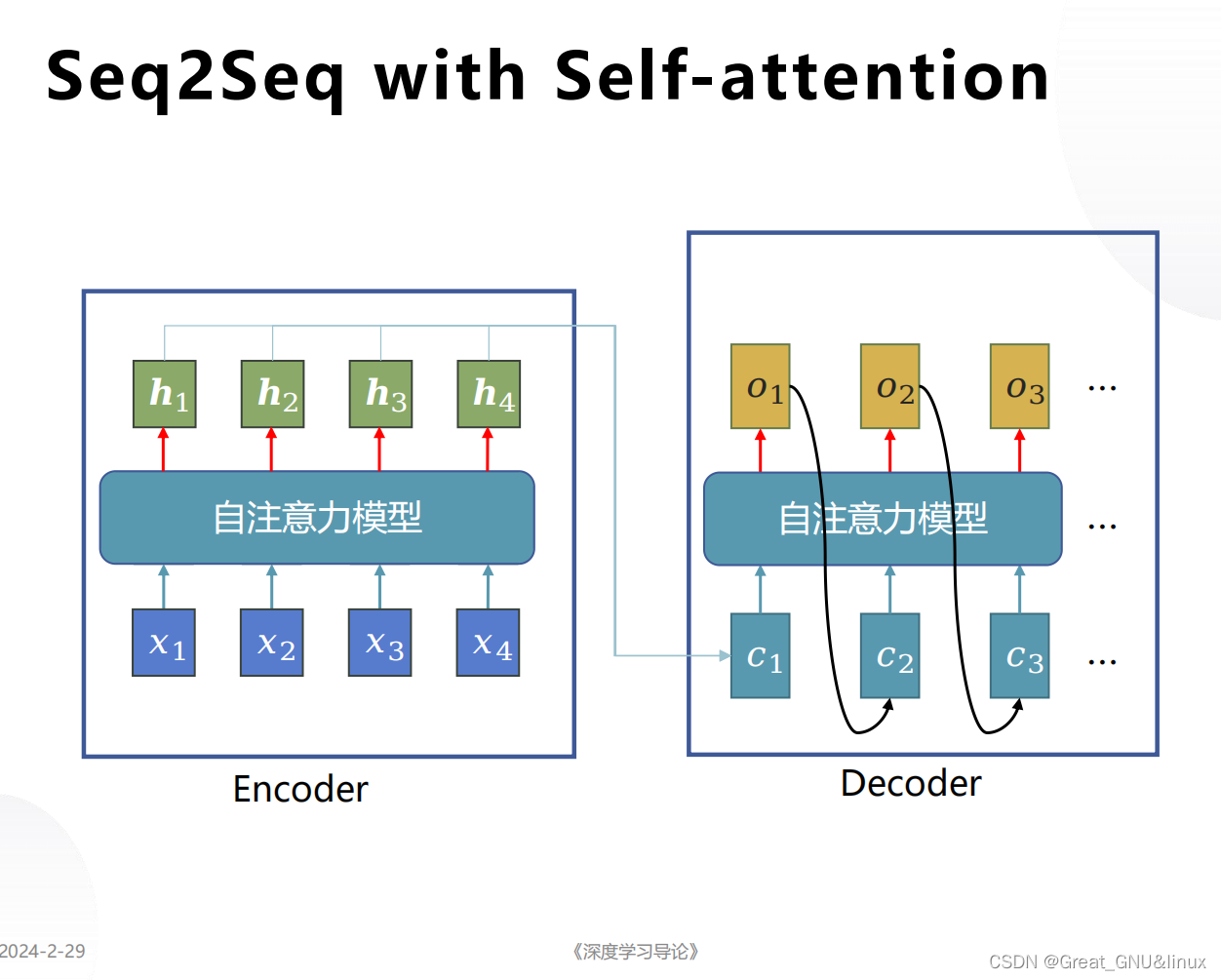
NLP(一)——概述
参考书: 《speech and language processing》《统计自然语言处理》 宗成庆 语言是思维的载体,自然语言处理相比其他信号较为特别 word2vec用到c语言 Question 预训练语言模型和其他模型的区别? 预训练模型是指在大规模数据上进行预训练的模型,通常…...

智慧公厕:打造智慧城市的环卫明珠
在城市建设中,公共卫生设施的完善和智能化一直是重要环节。而智慧公厕作为智慧城市建设的重要组成部分,发挥着不可替代的作用。本文以智慧公厕源头实力厂家广州中期科技有限公司,大量精品案例现场实景实图,解读智慧公厕如何助力打…...
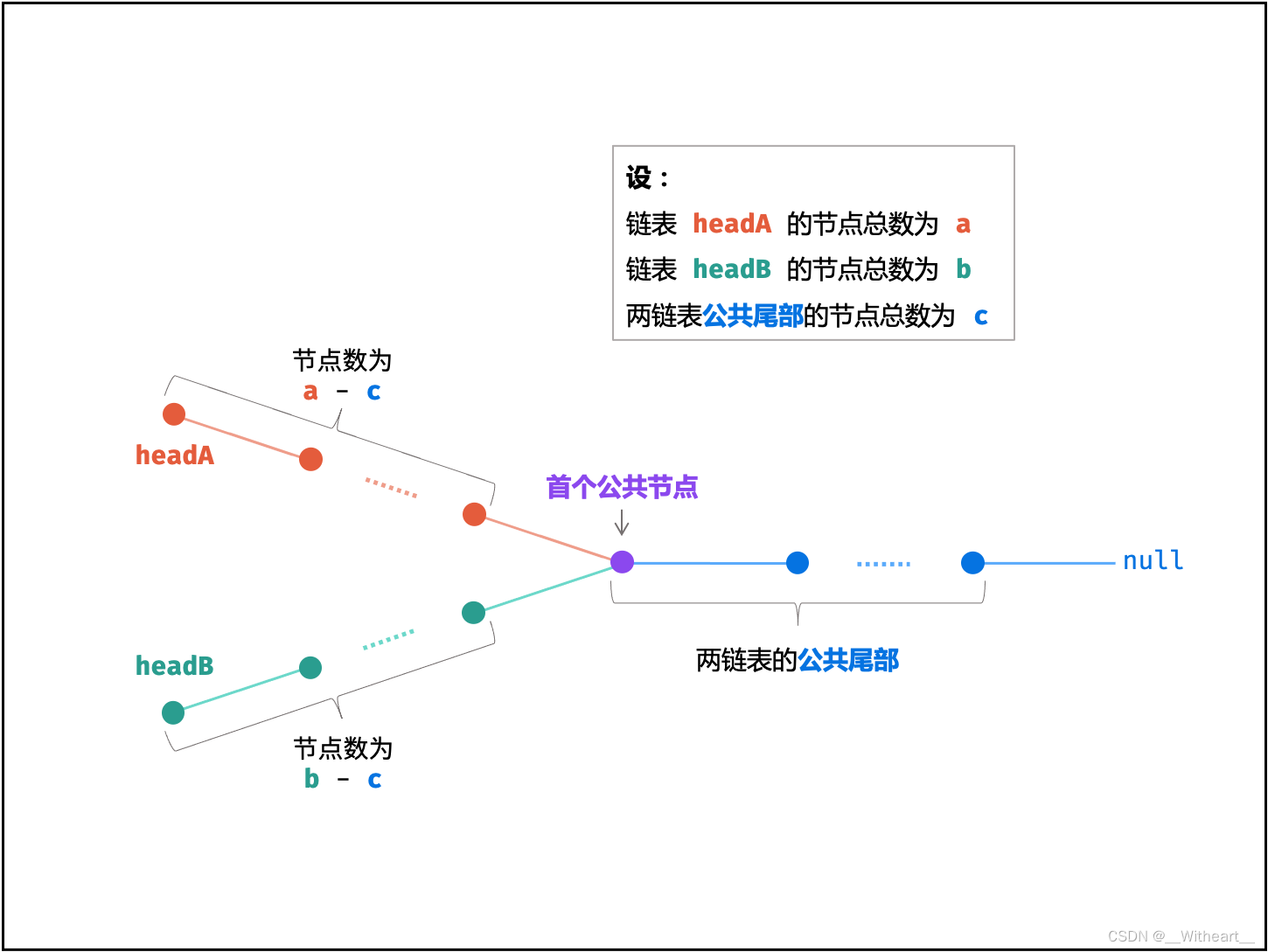
[LeetBook]【学习日记】寻找链表相交节点
来源于「Krahets」的《图解算法数据结构》 https://leetcode.cn/leetbook/detail/illustration-of-algorithm/ 本题与主站 160 题相同:https://leetcode-cn.com/problems/intersection-of-two-linked-lists/ 训练计划 V 某教练同时带教两位学员,分别以…...
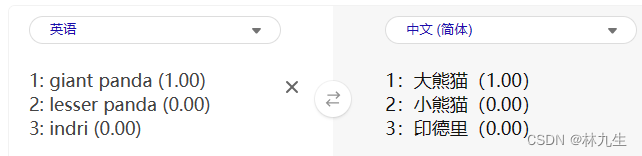
【Python】OpenCV-使用ResNet50进行图像分类
使用ResNet50进行图像分类 如何使用ResNet50模型对图像进行分类。 import os import cv2 import numpy as np from tensorflow.keras.applications.resnet50 import ResNet50, preprocess_input, decode_predictions from tensorflow.keras.preprocessing import image# 设置…...

TypeError: `dumps_kwargs` keyword arguments are no longer supported
TypeError: dumps_kwargs keyword arguments are no longer supported 1. 问题描述2. 解决方法 1. 问题描述 使用 FastChat 启动私有大语言模型,通过一些 UI 工具进行访问时,报以下错误。 略 2024-02-29 09:26:14 | ERROR | stderr | yield f"…...

设计模式学习笔记 - 设计原则 - 3.里氏替换原则,它和多态的区别是什么?
前言 今天来学习 SOLID 中的 L:里氏替换原则。它的英文翻译是 Liskov Substitution Principle,缩写为 LSP。 英文原话是: Functions that use points of references of base classes must be able to use objects of derived classes withou…...
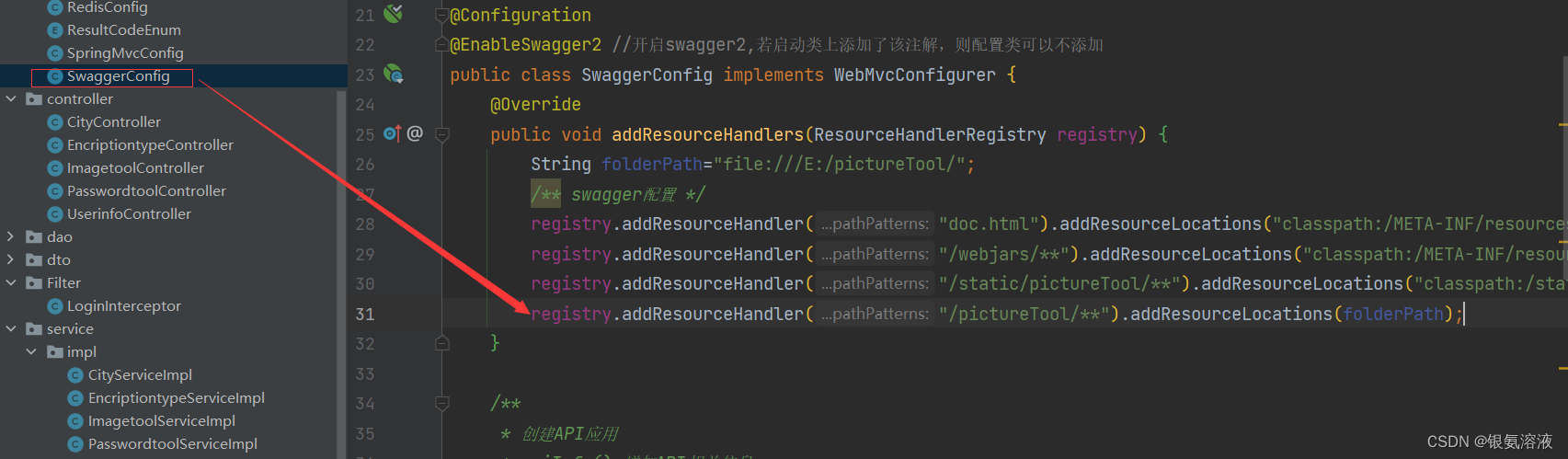
java实现图片转pdf,并通过流的方式进行下载(前后端分离)
首先需要导入相关依赖,由于具体依赖本人也不是记得很清楚了,所以简短的说一下。 iText:PDF 操作库,用于创建和操作 PDF 文件。可通过 Maven 或 Gradle 引入 iText 依赖。 MultipartFile:Spring 框架中处理文件上传的类…...

如何系统的学习Python——Python的基本语法
学习Python的基本语法是入门的第一步,以下是一些常见的基本语法概念: 注释: 用#符号来添加单行注释,或使用三引号(或""")来添加多行注释。 # 这是一个单行注释 这是 多行 注释 变量和数据类型: 变量用…...

相机,棱镜和光场
一、成像方法 Imaging Synthesis Capture 1.Synthesis(图形学上)合成:比如之前学过的光线追踪或者光栅化 2.Capture(捕捉):把真实世界存在的东西捕捉成为照片 二、相机 1.小孔成像 利用小孔成像的相…...
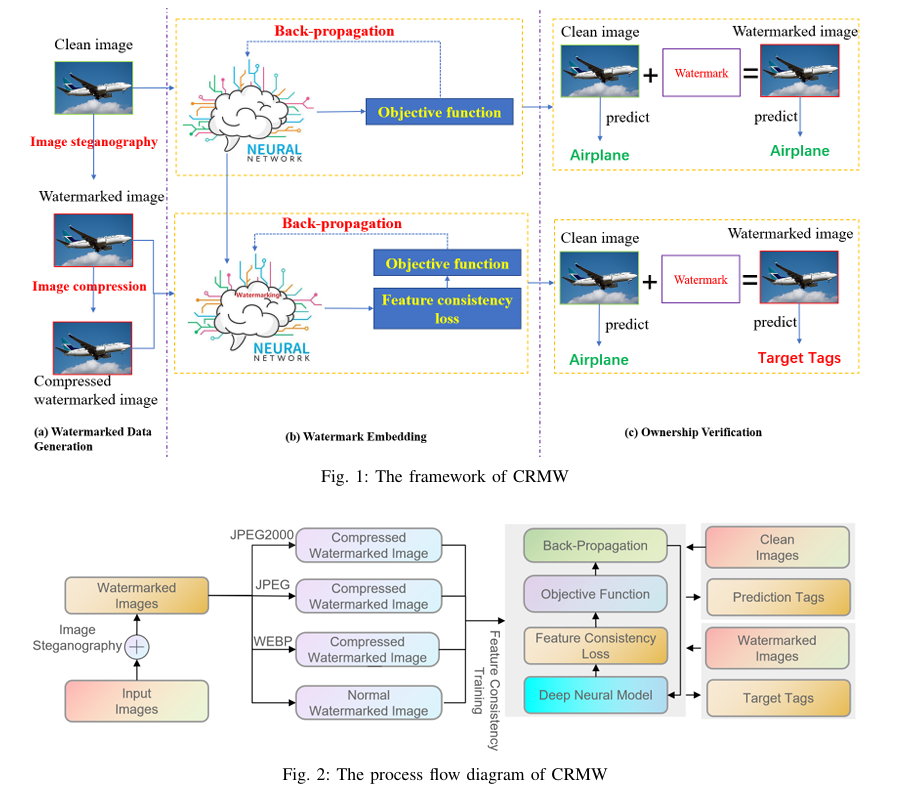
【图像版权】论文阅读:CRMW 图像隐写术+压缩算法
不可见水印 前言背景介绍ai大模型水印生成产物不可见水印CRMW 在保护深度神经网络模型知识产权方面与现有防御机制有何不同?使用图像隐写术和压缩算法为神经网络模型生成水印数据集有哪些优势?特征一致性训练如何发挥作用,将水印数据集嵌入到…...

代码随想录算法训练营第31天—贪心算法05 | ● 435. 无重叠区间 ● *763.划分字母区间 ● *56. 合并区间
435. 无重叠区间 https://programmercarl.com/0435.%E6%97%A0%E9%87%8D%E5%8F%A0%E5%8C%BA%E9%97%B4.html 考点 贪心算法重叠区间 我的思路 先按照区间左坐标进行排序,方便后续处理进行for循环,循环范围是0到倒数第二个元素如果当前区间和下一区间重叠…...

2024《》
vue-cli到哪做了那些事 vue-cli是vue.js的脚手架,用于自动生成vue.jswebpack的项目模板,快速搭建Vue.js项目。 vue cli内置了webpack的一些功能,这些是用webpack打包时需要我们自己配置的,例如: 1.ES6代码转换成ES5代…...

【Web】Java反序列化之从CC3看TemplatesImpl的利用
目录 关于TemplatesImpl 关于TemplatesImpl加载字节码 CC3链分析 纯CC3demo 根据CC3改CC6 关于TemplatesImpl TemplatesImpl 是 Java 中的一个类,通常与 Java 反序列化漏洞相关的攻击中被使用。该类位于 Java 标准库中的 javax.xml.transform 包下。 在 Java…...

【Elasticsearch索引】Recovery恢复索引
文章目录 索引恢复恢复列表获取恢复信息响应详细信息正在进行的恢复响应解析高级设置 本地分片恢复事务日志 索引恢复 索引恢复提供了对正在进行的索引分片恢复的洞察。恢复状态可以针对特定的索引报告,也可以在集群范围内报告。 恢复列表 recovery命令是索引分片…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
