支持向量机 SVM | 线性可分:硬间隔模型公式推导
目录
- 一. SVM的优越性
- 二. SVM算法推导
- 小节
- 概念
在开始讲述SVM算法之前,我们先来看一段定义:
'''
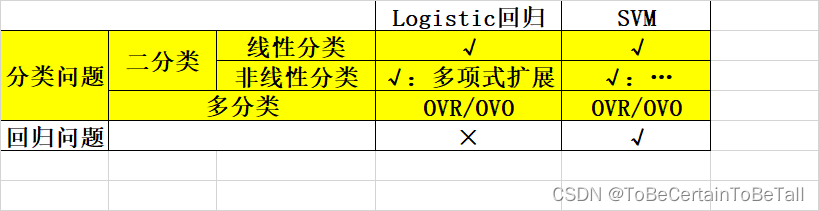
支持向量机(Support VecorMachine, SVM)本身是一个二元分类算法,支持线性分类和非线性分类的分类应用,同时通过OvR或者OvO的方式可以应用在多元分类领域中能够直接将SVM应用于回归应用中
在不考虑集成学习算法或者特定的数据集时,SVM在分类算法中可以说是一种特别优秀的算法
'''
一. SVM的优越性
在Logistic回归算法中:
我们追求是寻找一条决策边界,即找到一条能够正确划分所有训练样本的边界;
当所有样本正确划分时,损失函数已降至最低,模型不再优化
在SVM算法中:
我们追求是寻找一条最优决策边界
那什么是最优呢?SVM提出的基本思想是,寻找一条决策边界,使得该边界到两边最近的点间隔最大这样做得目的在于:相比于其他边界,svm寻找到的边界对于样本的局部扰动容忍性最好,对新进样本更容易判断正确;也就是说,此时决策边界具有最好的鲁棒性

二. SVM算法推导
注意:下面讲述的是线性分类
这里我们换一种思路寻找最佳决策边界:
首先假设决策边界为
y = ω → ⋅ x → + b y= \overrightarrow{\omega }\cdot \overrightarrow{x} +b y=ω⋅x+b
公式解释1:
为什么要这么设方程呢?我们希望通过向量点乘来确定距离
换句话说,希望通过向量点乘来确定正负样本的边界
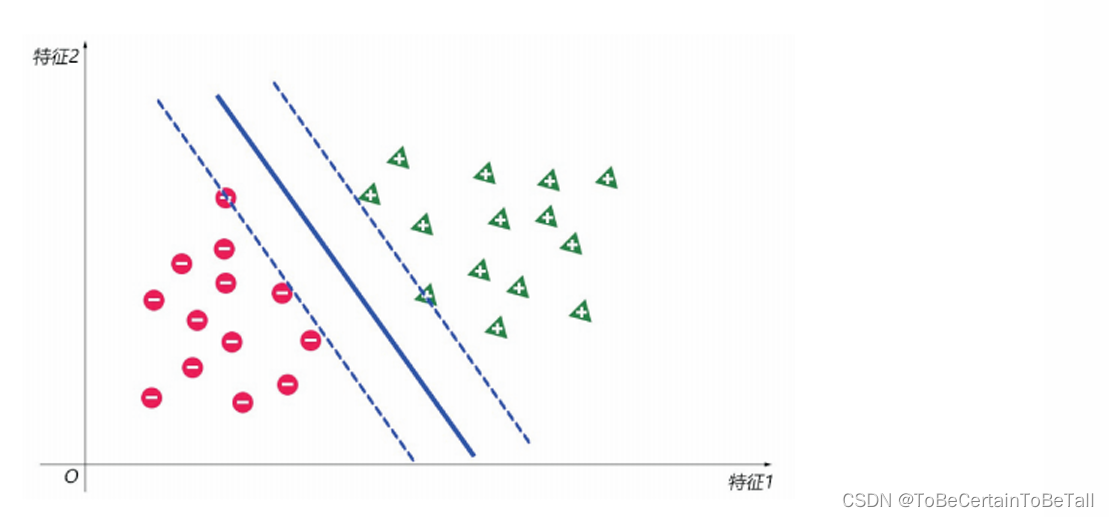
为了寻找最佳决策边界,我们可以:
以上述决策边界为中心线,向两边做平行线,让这两条平行线过两边最近的样本点;此时会形成一条“街道”,最佳决策边界就是使这条街道最宽的那个决策边界。
补充一点:
在Logistic回归算法中,我们人为的将数据集设为1,0
在SVM算法中,我们人为的将数据集设为1,-1
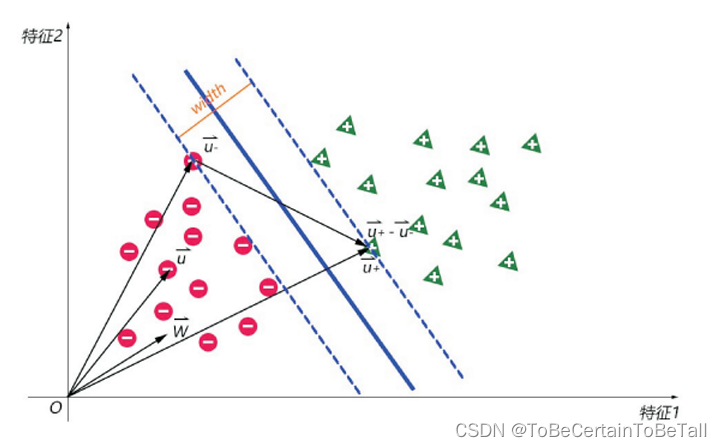
参数说明:width:街宽
ω → \overrightarrow{\omega } ω:决策边界的法向量
u − → \overrightarrow{u_{-} } u−:街边上的负样本向量
u + → \overrightarrow{u_{+} } u+:街边上的正样本向量
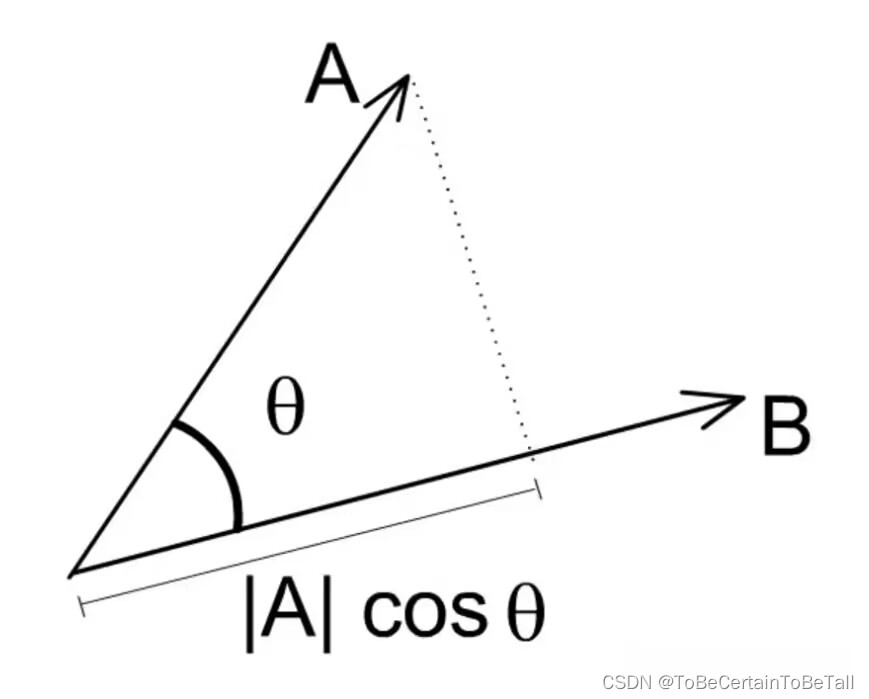
单位向量: a → ∥ a ∥ \frac{\overrightarrow{a}}{\left \| a \right \| } ∥a∥a向量点乘几何的意义:
a → ⋅ b → = ∣ a → ∣ ∣ b → ∣ cos θ \overrightarrow{a}\cdot \overrightarrow{b} =\left | \overrightarrow{a} \right| |\overrightarrow{b} | \cos \theta a⋅b= a ∣b∣cosθ
可以理解为 a → \overrightarrow{a} a 在 b → \overrightarrow{b} b上的投影长度乘以 ∣ b → ∣ |\overrightarrow{b}| ∣b∣的模长
对于训练集中的任何一个数据,我们总会取到一个合适长度的 ω → \overrightarrow{\omega } ω,以及一个适合的常数b,得到:
{ ω → ⋅ u + → + b ≥ 1 ω → ⋅ u − → + b ≤ − 1 \left\{\begin{matrix}\overrightarrow{\omega }\cdot \overrightarrow{u_{+} } +b\ge 1 \\\overrightarrow{\omega }\cdot \overrightarrow{u_{-} } +b\le -1 \end{matrix}\right. {ω⋅u++b≥1ω⋅u−+b≤−1
即可以合并为: y i ( ω → ⋅ u i → + b ) ≥ 1 y_{i} (\overrightarrow{\omega }\cdot \overrightarrow{u_{i} } +b)\ge1 yi(ω⋅ui+b)≥1
而对于街边点而言,满足
y i ( ω → ⋅ u i → + b ) = 1 y_{i} (\overrightarrow{\omega }\cdot \overrightarrow{u_{i} } +b)=1 yi(ω⋅ui+b)=1
注意:这些街边点对于决定决策边界取决定性作用,因此被称为支持向量
这样,我们就可以用数学方式将上述街宽抽象出来:
w i d t h = ( u + → − u − → ) ⋅ w → ∥ w ∥ width = (\overrightarrow{u_{+}}-\overrightarrow{u_{-}} )\cdot \frac{\overrightarrow{w}}{\left \| w \right \| } width=(u+−u−)⋅∥w∥w
推导式子,就可以进一步得到:
w i d t h = ( u + → − u − → ) ⋅ w → ∥ w ∥ width = (\overrightarrow{u_{+}}-\overrightarrow{u_{-}} )\cdot \frac{\overrightarrow{w}}{\left \| w \right \| } width=(u+−u−)⋅∥w∥w
= u + → ⋅ ω → ∥ ω → ∥ − u − → ⋅ ω → ∥ ω → ∥ =\frac{\overrightarrow{u_{+}}\cdot\overrightarrow{\omega _{}} }{\left \| \overrightarrow{\omega\mathrm{} } \right \| }-\frac{\overrightarrow{u_{-}}\cdot\overrightarrow{\omega _{}} }{\left \| \overrightarrow{\omega\mathrm{} } \right \| } =∥ω∥u+⋅ω−∥ω∥u−⋅ω
= 1 − b ∥ w → ∥ − − 1 − b ∥ w → ∥ =\frac{1-b}{\left \| \overrightarrow{w} \right \| } -\frac{-1-b}{\left \| \overrightarrow{w} \right \| } =∥w∥1−b−∥w∥−1−b
= 2 ∥ w → ∥ =\frac{2}{\left \| \overrightarrow{w} \right \| } =∥w∥2
此时,我们要求街宽最大,即是求 m i n ( ∥ w → ∥ ) min({\left \| \overrightarrow{w} \right \| }) min( w ),这里为了后续求导方便,将值写成 m i n ( 1 2 ∥ w → ∥ 2 ) min(\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2} ) min(21 w 2)
需要明确,"街边"最大值的条件是基于支持向量的,而支持向量是属于数据集的,因此我们的问题就变成了:
{ m i n ( 1 2 ∥ w → ∥ 2 ) s . t . y i ( ω → ⋅ x → + b ) − 1 ≥ 0 \left\{\begin{matrix}min(\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2} ) \\s.t. y_{i} (\overrightarrow{\omega }\cdot \overrightarrow{x } +b)-1\ge0 \end{matrix}\right. {min(21 w 2)s.t.yi(ω⋅x+b)−1≥0
这是一个典型的条件极值问题,我们用拉格朗日乘数法,得到拉格朗日函数为:
L = 1 2 ∥ w → ∥ 2 − ∑ i = 1 m β i [ y i ( ω → ⋅ x → + b ) − 1 ] , ( β i ≥ 0 ) L = \frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2} -\sum_{i=1}^{m} \beta _{i}[ y_{i} (\overrightarrow{\omega }\cdot \overrightarrow{x } +b)-1] ,(\beta _{i}\ge 0) L=21 w 2−i=1∑mβi[yi(ω⋅x+b)−1],(βi≥0)
这里的约束是不等式约束,所以要使用KKT条件(KKT是拉格朗日乘数法的一种泛化形式,此时 β i ≥ 0 \beta _{i}\ge0 βi≥0),而KKT条件的计算方式为: max β ≥ 0 min w , b L ( w , b , β ) \max_{\beta \ge 0} \min_{w,b}L(w,b,\beta ) β≥0maxw,bminL(w,b,β)
∂ L ∂ w = w − ∑ i = 1 m β i x ( i ) y ( i ) = 0 ⇒ w = ∑ i = 1 m β i x ( i ) y ( i ) \frac{\partial L}{\partial w} =w-\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)}=0\Rightarrow w=\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} ∂w∂L=w−i=1∑mβix(i)y(i)=0⇒w=i=1∑mβix(i)y(i)
∂ L ∂ b = − ∑ i = 1 m β i y ( i ) = 0 ⇒ 0 = ∑ i = 1 m β i y ( i ) \frac{\partial L}{\partial b} =-\sum_{i=1}^{m} \beta _{i}y^{(i)}=0\Rightarrow 0=\sum_{i=1}^{m} \beta _{i} y^{(i)} ∂b∂L=−i=1∑mβiy(i)=0⇒0=i=1∑mβiy(i)
公式解释:
β \beta β是每个样本对应的拉格朗日乘子对于非支持向量而言, β = 0 \beta=0 β=0,即对非支持向量无约束
则: y ( i ) ∗ 0 = 0 y^{(i)}*0=0 y(i)∗0=0
对于支持向量而言, β > 0 \beta>0 β>0,即对支持向量有约束
则: 正样本支持向量 ∗ 1 + 负样本支持向量 ∗ ( − 1 ) = 0 正样本支持向量\ast 1+负样本支持向量\ast (-1)=0 正样本支持向量∗1+负样本支持向量∗(−1)=0
此时 L ( β ) L(\beta) L(β)为:
L ( β ) = 1 2 ∥ w → ∥ 2 − ∑ i = 1 m β i [ y ( i ) ( ω T ⋅ x ( i ) + b ) − 1 ] L(\beta)=\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2} -\sum_{i=1}^{m} \beta _{i}[y^{(i)} (\omega ^{T} \cdot x^{(i)} +b)-1] L(β)=21 w 2−∑i=1mβi[y(i)(ωT⋅x(i)+b)−1]
= 1 2 ω T ω − ∑ i = 1 m β i y ( i ) ω T ⋅ x ( i ) − b ∑ i = 1 m β i y ( i ) + ∑ i = 1 m β i =\frac{1}{2}\omega ^{T}\omega -\sum_{i=1}^{m} \beta _{i}y^{(i)}\omega ^{T} \cdot x^{(i)}-b\sum_{i=1}^{m} \beta _{i}y^{(i)}+\sum_{i=1}^{m} \beta _{i} =21ωTω−∑i=1mβiy(i)ωT⋅x(i)−b∑i=1mβiy(i)+∑i=1mβi
= 1 2 ω T ∑ i = 1 m β i x ( i ) y ( i ) − ∑ i = 1 m β i y ( i ) ω T x ( i ) + ∑ i = 1 m β i =\frac{1}{2}\omega ^{T}\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} -\sum_{i=1}^{m} \beta _{i}y^{(i)}\omega ^{T}x^{(i)}+\sum_{i=1}^{m} \beta _{i} =21ωT∑i=1mβix(i)y(i)−∑i=1mβiy(i)ωTx(i)+∑i=1mβi
= − 1 2 ω T ∑ i = 1 m β i x ( i ) y ( i ) + ∑ i = 1 m β i =-\frac{1}{2}\omega ^{T}\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} +\sum_{i=1}^{m} \beta _{i} =−21ωT∑i=1mβix(i)y(i)+∑i=1mβi
= − 1 2 ( ∑ j = 1 m β j x ( j ) y ( j ) ) T ( ∑ i = 1 m β i x ( i ) y ( i ) ) + ∑ i = 1 m β i =-\frac{1}{2}(\sum_{j=1}^{m} \beta _{j} x^{(j)}y^{(j)})^{T}(\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} )+\sum_{i=1}^{m} \beta _{i} =−21(∑j=1mβjx(j)y(j))T(∑i=1mβix(i)y(i))+∑i=1mβi
= − 1 2 ∑ j = 1 m β j x ( j ) T y ( j ) ∑ i = 1 m β i x ( i ) y ( i ) + ∑ i = 1 m β i =-\frac{1}{2}\sum_{j=1}^{m} \beta _{j} x^{(j)^{T}}y^{(j)}\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} +\sum_{i=1}^{m} \beta _{i} =−21∑j=1mβjx(j)Ty(j)∑i=1mβix(i)y(i)+∑i=1mβi
= ∑ i = 1 m β i − 1 2 ∑ i = 1 m ∑ j = 1 m β i β j y ( i ) y ( j ) x ( j ) T x ( i ) =\sum_{i=1}^{m} \beta _{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}x^{(j)^{T}} x^{(i)} =∑i=1mβi−21∑i=1m∑j=1mβiβjy(i)y(j)x(j)Tx(i)
即: { L ( β ) = ∑ i = 1 m β i − 1 2 ∑ i = 1 m ∑ j = 1 m β i β j y ( i ) y ( j ) x ( j ) T x ( i ) s . t : ∑ i = 1 m β i y ( i ) = 0 \left\{\begin{matrix}L(\beta)=\sum_{i=1}^{m} \beta _{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}x^{(j)^{T}} x^{(i)} \\s.t:\sum_{i=1}^{m} \beta _{i} y^{(i)}=0 \end{matrix}\right. {L(β)=∑i=1mβi−21∑i=1m∑j=1mβiβjy(i)y(j)x(j)Tx(i)s.t:∑i=1mβiy(i)=0
解到这一步,我们发现L函数只与 β \beta β有关,所以此时可以直接极大化我们的优化函数,且
max β ≥ 0 l ( β ) ⟶ min β ≥ 0 − l ( β ) \max_{\beta \ge 0}l(\beta ) \longrightarrow \min_{\beta \ge 0}-l(\beta ) β≥0maxl(β)⟶β≥0min−l(β)
因此,求解 β \beta β就变成了
{ min β ≥ 0 1 2 ∑ i = 1 m ∑ j = 1 m β i β j y ( i ) y ( j ) x ( j ) T x ( i ) − ∑ i = 1 m β i s . t : ∑ i = 1 m β i y ( i ) = 0 \left\{\begin{matrix}\min_{\beta \ge 0}\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}x^{(j)^{T}} x^{(i)}-\sum_{i=1}^{m} \beta _{i} \\s.t:\sum_{i=1}^{m} \beta _{i} y^{(i)}=0 \end{matrix}\right. {minβ≥021∑i=1m∑j=1mβiβjy(i)y(j)x(j)Tx(i)−∑i=1mβis.t:∑i=1mβiy(i)=0
但是对于 β \beta β,可以使用SMO算法求得;对于SMO算法,我们先放一放
这里,假设我们用SMO求得了 β \beta β的最优解,那么我们可以分别计算得到对应的:
w = ∑ i = 1 m β i x ( i ) y ( i ) w=\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} w=∑i=1mβix(i)y(i)
b:一般使用所有支持向量的计算均值作为实际值
怎么得到支持向量呢?
β = 0 \beta=0 β=0,该样本不是支持向量
β > 1 \beta>1 β>1,该样本是支持向量
小节
对于线性可分的m个样本(x1,y1),(x2,y2)… :
x为n维的特征向量y为二元输出,即+1,-1
SVM的输出为w,b,分类决策函数
通过构造约束问题:
{ min β ≥ 0 1 2 ∑ i = 1 m ∑ j = 1 m β i β j y ( i ) y ( j ) x ( j ) T x ( i ) − ∑ i = 1 m β i s . t : ∑ i = 1 m β i y ( i ) = 0 \left\{\begin{matrix}\min_{\beta \ge 0}\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}x^{(j)^{T}} x^{(i)}-\sum_{i=1}^{m} \beta _{i} \\s.t:\sum_{i=1}^{m} \beta _{i} y^{(i)}=0 \end{matrix}\right. {minβ≥021∑i=1m∑j=1mβiβjy(i)y(j)x(j)Tx(i)−∑i=1mβis.t:∑i=1mβiy(i)=0
使用SMO算法求出上述最优解 β \beta β
找到所有支持向量集合:
S = ( x ( i ) , y ( i ) ) ( β > 0 , i = 1 , 2 , . . . , m ) S = (x^{(i)}, y^{(i)}) (\beta > 0,i=1,2,...,m) S=(x(i),y(i))(β>0,i=1,2,...,m)
从而更新w,b
w = ∑ i = 1 m β i x ( i ) y ( i ) w=\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} w=∑i=1mβix(i)y(i)
b = 1 S ∑ i = 1 S ( y s − ∑ i = 1 m β i x ( i ) T y ( i ) x s ) b=\frac{1}{S} \sum_{i=1}^{S}(y^{s}- \sum_{i=1}^{m} \beta _{i} x^{(i)^{T}}y^{(i)}x^{s} ) b=S1∑i=1S(ys−∑i=1mβix(i)Ty(i)xs)
构造最终的分类器,为:
f ( x ) = s i g n ( w ∗ x + b ) f(x)=sign(w\ast x+b) f(x)=sign(w∗x+b)
x<0时,y=-1x=0时,y=0x>0时,y=1注意:假设,不会出现0若出现,正负样本随意输出一个,即+0.00000001或-0.00000001都可以
概念
最后,我们定义具体概念:
分割超平面(Separating Hyperplane):将数据集分割开来的直线、平面叫分割超平面
支持向量(Support Vector):离分割超平面最近的那些点叫做支持向量
间隔(Margin):支持向量数据点到分割超平面的距离称为间隔;任何一个支持向量到分割超平面的距离都是相等的
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
本文相关代码存放位置
祝愉快🌟!
相关文章:
支持向量机 SVM | 线性可分:硬间隔模型公式推导
目录 一. SVM的优越性二. SVM算法推导小节概念 在开始讲述SVM算法之前,我们先来看一段定义: 支持向量机(Support VecorMachine, SVM)本身是一个二元分类算法,支持线性分类和非线性分类的分类应用,同时通过OvR或者OvO的方式可以应用…...
【Unity实战】UGUI和Z轴排序那点事儿
如果读者是从Unity 4.x时代过来的,可能都用过NGUI这个插件(后来也是土匪成了正规军),NGUI一大特点是可以靠transform位移的Z值进行遮挡排序,然而这个事情在UGUI成了难题(Sorting Layer、Inspector顺序等因素…...

Vue/React 前端高频面试
说一说vue钩子函数 钩子函数是Vue实例创建和销毁过程中自动执行的函数。按照组件生命周期的过程分为:挂载阶段 -> 更新阶段 -> 销毁阶段。 每个阶段对应的钩子函数分别为:挂载阶段(beforeCreate,created,befor…...
[技巧]Arcgis之图斑四至范围批量计算
ArcGIS图层(点、线、面三类图形)四至范围计算 例外一篇介绍:[技巧]Arcgis之图斑四至点批量计算 说明:如下图画出来的框(范围标记不是很准) ,图斑的x最大和x最小,y最大,…...
C/C++工程师面试题(STL篇)
STL 中有哪些常见的容器 STL 中容器分为顺序容器、关联式容器、容器适配器三种类型,三种类型容器特性分别如下: 1. 顺序容器 容器并非排序的,元素的插入位置同元素的值无关,包含 vector、deque、list vector:动态数组…...

Effective Programming 学习笔记
1 基本语句 1.1 断言 在南溪看来,断言可以用来有效地确定编程中当前代码运行的前置条件,尤其是以下情况: 第三方工具库对输入数据的依赖,例如:minitouch库对Android版本的要求...
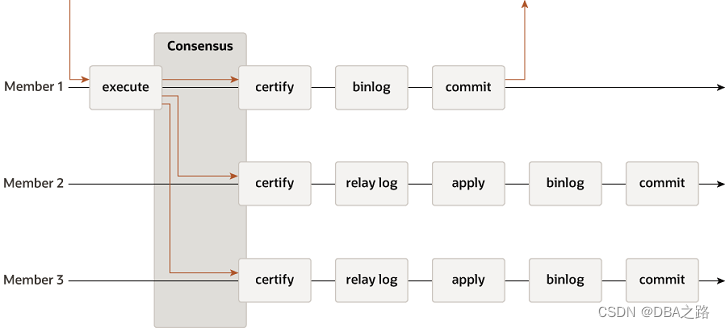
【MGR】MySQL Group Replication 背景
目录 17.1 Group Replication Background 17.1.1 Replication Technologies 17.1.1.1 Primary-Secondary Replication 17.1.1.2 Group Replication 17.1.2 Group Replication Use Cases 17.1.2.1 Examples of Use Case Scenarios 17.1.3 Group Replication Details 17.1…...

300分钟吃透分布式缓存-17讲:如何理解、选择并使用Redis的核心数据类型?
Redis 数据类型 首先,来看一下 Redis 的核心数据类型。Redis 有 8 种核心数据类型,分别是 : & string 字符串类型; & list 列表类型; & set 集合类型; & sorted set 有序集合类型&…...

思科网络设备监控
思科是 IT 行业的先驱之一,提供从交换机到刀片服务器的各种设备,以满足中小企业和企业的各种 IT 管理需求。管理充满思科的 IT 车间涉及许多管理挑战,例如监控可用性和性能、管理配置更改、存档防火墙日志、排除带宽问题等等,这需…...

深入剖析k8s-控制器思想
引言 本文是《深入剖析Kubernetes》学习笔记——《深入剖析Kubernetes》 正文 控制器都遵循K8s的项目中一个通用的编排模式——控制循环 for {实际状态 : 获取集群中对象X的实际状态期望状态 : 获取集群中对象X的期望状态if 实际状态 期望状态 {// do nothing} else {执行…...
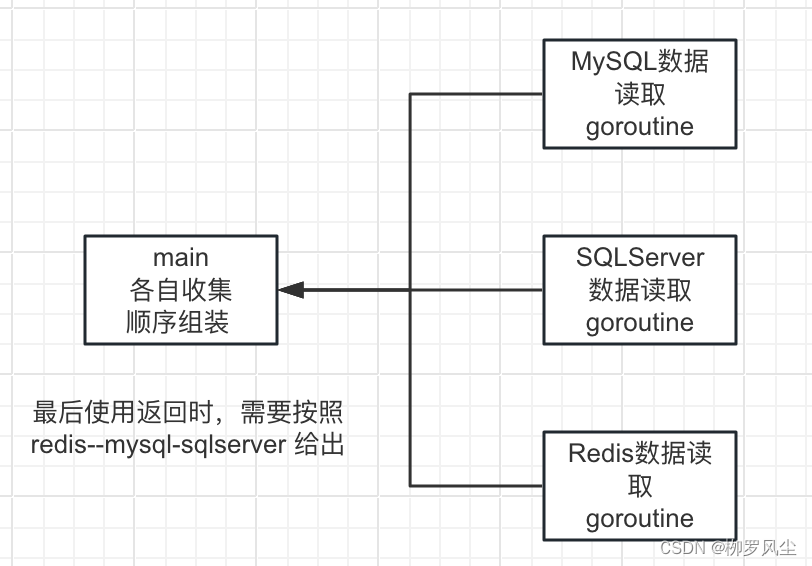
go并发模式之----使用时顺序模式
常见模式之二:使用时顺序模式 定义 顾名思义,起初goroutine不管是怎么个先后顺序,等到要使用的时候,需要按照一定的顺序来,也被称为未来使用模式 使用场景 每个goroutine函数都比较独立,不可通过参数循环…...
[动态规划]---part1
前言 作者:小蜗牛向前冲 专栏:小蜗牛算法之路 专栏介绍:"蜗牛之道,攀登大厂高峰,让我们携手学习算法。在这个专栏中,将涵盖动态规划、贪心算法、回溯等高阶技巧,不定期为你奉上基础数据结构…...
)
java 关于 Object 类中的 wait 和 notify 方法。(生产者和消费者模式!)
4、关于 Object 类中的 wait 和 notify 方法。(生产者和消费者模式!) 第一:wait 和 notify 方法不是线程对象的方法,是 java 中任何一个 java 对象都有的方法,因为这两个方法是 Object 类中自带的。 wait 方…...
YOLOv8姿态估计实战:训练自己的数据集
课程链接:https://edu.csdn.net/course/detail/39355 YOLOv8 基于先前 YOLO 版本的成功,引入了新功能和改进,进一步提升性能和灵活性。YOLOv8 同时支持目标检测和姿态估计任务。 本课程以熊猫姿态估计为例,将手把手地教大家使用C…...
【海贼王的数据航海:利用数据结构成为数据海洋的霸主】链表—双向链表
目录 往期 1 -> 带头双向循环链表(双链表) 1.1 -> 接口声明 1.2 -> 接口实现 1.2.1 -> 双向链表初始化 1.2.2 -> 动态申请一个结点 1.2.3 -> 双向链表销毁 1.2.4 -> 双向链表打印 1.2.5 -> 双向链表判空 1.2.6 -> 双向链表尾插 1.2.7 -&…...

做测试还是测试开发,选职业要慎重!
【软件测试面试突击班】2024吃透软件测试面试最全八股文攻略教程,一周学完让你面试通过率提高90%!(自动化测试) 突然发现好像挺多人想投测开和测试的,很多人面试的时候也会被问到这几个职位的区别,然后有测…...

Java面试题总结200道(二)
26、简述Spring中Bean的生命周期? 在原生的java环境中,一个新的对象的产生是我们用new()的方式产生出来的。在Spring的IOC容器中,将这一部分的工作帮我们完成了(Bean对象的管理)。既然是对象,就存在生命周期,也就是作用…...
面试数据库篇(mysql)- 03MYSQL支持的存储引擎有哪些, 有什么区别
存储引擎就是存储数据、建立索引、更新/查询数据等技术的实现方式 。存储引擎是基于表的,而不是基于库的,所以存储引擎也可被称为表类型。 MySQL体系结构 连接层服务层引擎层存储层 存储引擎特点 InnoDB MYSQL支持的存储引擎有哪些, 有什么区别 ? my…...

MySQL深入——25
Join语句如何优化? Join语句的两种算法,分别为Index Nested-Loop Join和Block Nested-Loop Join NLJ在大表Join当中还不错,但BNL在大表join时性能就差很多,很耗CPU资源。 如何优化这两个算法 创建t1,t2算法,在t1中…...

Docker运行时安全之道: 保障容器环境的安全性
引言 Docker作为容器化技术的领军者,为应用部署提供了灵活性和便捷性。然而,在享受这些优势的同时,必须重视Docker运行时的安全性。本文将深入研究一些关键的Docker运行时安全策略,以确保你的容器环境在生产中得到有效的保护。 1. 使用最小特权原则 保持容器以最小权限运…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
