Python线性代数数字图像和小波分析之二
要点
- 数学方程:数字信号和傅里叶分析,离散时间滤波器,小波分析
- Python代码实现及应用变换过程:
- 读取音频和处理音频波,使用Karplus-强算法制作吉他音频
- 离散傅里叶计算功能和绘制图示结果
- 计算波形傅里叶系数
- 正向和反向(逆)快速傅里叶FFT 实现和使用
- 位反转函数
- 正向和反向(逆)离散余弦变换
- 离散时间滤波器结果绘图
- 一维、二维和三维正向和反向(逆)离散小波变换
- 张量积将小波应用于图像,二维和三维张量积实现
离散傅里叶分析数字声音
数字声音
数字声音是一个序列 x = { x i } i = 0 N − 1 \boldsymbol{x}=\left\{x_i\right\}_{i=0}^{N-1} x={xi}i=0N−1,对应于记录的 a a a连续声音 f f f的测量值以每秒 f s f_s fs 测量的固定速率,即
x k = f ( k / f s ) , 对于 k = 0 , 1 , … , N − 1 . x_k=f\left(k / f_s\right), \quad \text { 对于 } k=0,1, \ldots, N-1 \text {. } xk=f(k/fs), 对于 k=0,1,…,N−1.
f s f_s fs 称为采样频率或采样率。数字声音中的组成部分称为样本,连续样本之间的时间称为采样周期,通常表示为 T s T_s Ts。测量声音也称为对声音进行采样。
数字声音的质量通常通过比特率(每秒的位数)来衡量,即采样率与用于存储每个样本的位数(二进制数字)的乘积。 采样率和数字格式都会影响最终声音的质量。 这些被封装在数字声音格式中。
观察Python合成声音
首先,合成是使用各种方法创建声音的行为。 我将重点关注加法合成,即通过将不同信号相加的方式进行合成。
我将使用的库是 Numpy 和 Scipy。 Numpy 是一个用于数值计算的库,而 Scipy 是一个我将用于信号处理并将数据转换为声音文件的库。 我还将安装 matplotlib 来绘制声音信号。 Pydub 是一个用于播放音频的库。 为了安装这些包,我将使用 pip 并创建一个虚拟环境。我使用的是 Python 3.10,因此请调整您的 Python 安装说明。 在终端中,我们首先创建一个目录,然后创建一个 virtualenv 并安装必需的软件包。
请创建一个名为 sound.py 的新文件并在文本编辑器中打开它。这将是我用来合成声音的主文件。现在让我首先添加需要的导入。
import numpy as np
from scipy.io.wavfile import write
from scipy import signal
import matplotlib.pyplot as plt
让我们来回顾一下什么是声音。 声音是空气穿过空间的压力波。 它是一种称为纵波的波,意味着它垂直于传播方向移动。
声音可以表示为信号。 信号是一组随时间变化的数字,通常用方括号表示,例如 x [ n ] x[n] x[n]。 我们可以将信号设置为始终等于 1,例如 x [ n ] x[n] x[n]=1,或者创建一个像 x [ n ] x[n] x[n] = n n n 这样变化的线性信号。 出于我们的目的,我们将处理像正弦这样的周期性信号。 它们的形式为 x [ n ] x[n] x[n] = A s i n ( 2 π f n ) A sin(2πfn) Asin(2πfn),其中 A A A 是振幅, f f f 是频率。 信号的 y y y 轴是幅度或音量, x x x 轴是当前时间。
让我们尝试使用以下方程生成正弦波。
y [ n ] = A sin ( 2 π f t [ n ] ) y[n]=A \sin (2 \pi f t[n]) y[n]=Asin(2πft[n])
A 是幅度,f 是信号的频率。 频率是每秒的样本数。 它决定了声音的音调,较低的频率有更多的低音,较高的频率有更多的高音。 为该声音生成波形文件的代码如下所示。
AUDIO_RATE = 44100
freq = 440
length = 1# create time values
t = np.linspace(0, length, length * AUDIO_RATE, dtype=np.float32)
# generate y values for signal
y = np.sin(2 * np.pi * freq * t)
# save to wave file
write("sine.wav", AUDIO_RATE, y)
我们首先有音频速率常数,也称为采样率,它是声卡从麦克风或其他音频输入源采样音频的速率。 在本例中,频率将为 44,100Hz。 赫兹 (Hz) 是频率的标准度量,是大多数声卡上每秒的样本数。 其原因是人类听觉的限制和奈奎斯特采样定理。 其中指出,要播放频率最多为 f 的声音,我们至少需要 2f 个样本。 人的听觉通常敏感度为20,000Hz,这意味着采样率需要在40,000Hz以上。
这意味着我们需要在几秒内生成相当于音频剪辑长度 44,100 倍的样本数量。 在本例中,我们需要 1 秒的音频剪辑,因此需要将音频速率乘以 1。这将使我们能够生成跨越人类听觉范围的声音。
我们使用 linspace 生成时间值,范围从 0 到 1,样本数为 1 * AUDIO_RATE,即 44100 个样本。 然后使用每个时间值的 sin 计算信号。 频率为440Hz,即中A。然后我们可以使用Scipy中的write函数和相应的AUDIO_RATE将声音写入波形文件。
如果您听 sine.wav,您会听到短促的一秒正弦波声音。 这听起来像是扬声器发出蜂鸣声,如果您听不到它,请检查以确保代码正确并且您的音频设置也正确。 您的音频格式可能需要在设置中设置为 44,100Hz。
让我们使用 matplotlib 中的绘图函数绘制信号。
def plot(ts, ys, title, num_samples):plt.xlabel("t")plt.ylabel("y")plt.title(title)plt.plot(ys[:num_samples])plt.show()plot(t, y, "Sine Signal", 512)
如果我们绘制前 512 个样本,这就是我们得到的图。
方波类似,但我们使用方形而不是正弦曲线。这使用阶跃函数代替正弦函数来计算。我们可以使用正弦函数和 Heaviside 阶跃函数来实现这一点。
y = np.heaviside(np.sin(2 * np.pi * freq * t), 1.0)
我们可以使用 Scipy 的 signal.square 函数实现同样的效果。
t = np.linspace(0, length, length * AUDIO_RATE, dtype=np.float32)# generate y values for signal
y = signal.square(2 * np.pi * freq * t)
# save to wave file
write("square.wav", AUDIO_RATE, y)plot(t, y, "Square Signal", 512)
方波会产生比正弦波更刺耳的嗡嗡声。这是因为方波比只有一种音调的正弦波有更多的泛音。
离散傅里叶分析
在离散傅里叶分析中,向量 x = ( x 0 , … , x N − 1 ) \boldsymbol{x}=\left(x_0, \ldots, x_{N-1}\right) x=(x0,…,xN−1) 表示为 N N N 个向量的线性组合
ϕ n = 1 N ( 1 , e 2 π i n / N , e 2 π i 2 n / N , … , e 2 π i k n / N , … , e 2 π i n ( N − 1 ) / N ) \phi_n=\frac{1}{\sqrt{N}}\left(1, e^{2 \pi i n / N}, e^{2 \pi i 2 n / N}, \ldots, e^{2 \pi i k n / N}, \ldots, e^{2 \pi i n(N-1) / N}\right) ϕn=N1(1,e2πin/N,e2πi2n/N,…,e2πikn/N,…,e2πin(N−1)/N)
这些向量称为归一化复指数,或 N N N 阶纯数字音调。 n n n也称为频率指数。整个集合 F N = { ϕ n } n = 0 N − 1 \mathcal{F}_N=\left\{\phi_n\right\}_{n=0}^{N-1} FN={ϕn}n=0N−1称为 N N N点傅里叶基。
请注意,纯数字音可以被视为纯音的样本,在一个周期内均匀采集: f ( t ) = e 2 π i n t / T / N f(t)=e^{2 \pi i n t / T} / \sqrt{N} f(t)=e2πint/T/N 是具有频率的纯音 n / T n / T n/T,其样本为
f ( k T / N ) = e 2 π i n ( k T / N ) / T N = e 2 π i n k / N N , f(k T / N)=\frac{e^{2 \pi i n(k T / N) / T}}{\sqrt{N}}=\frac{e^{2 \pi i n k / N}}{\sqrt{N}}, f(kT/N)=Ne2πin(kT/N)/T=Ne2πink/N,
将纯音映射到数字纯音时,索引 n n n 对应于频率 ν = n / T \nu=n / T ν=n/T, N N N 对应于一个周期内采集的样本数。由于 T f s = N T f_s=N Tfs=N,其中 f s f_s fs是采样频率,因此我们在频率和频率指数之间有以下联系:
ν = n f s N and n = ν N f s \nu=\frac{n f_s}{N} \text { and } n=\frac{\nu N}{f_s} ν=Nnfs and n=fsνN
以下引理表明傅立叶基是正交的,因此它确实是一个基。
离散傅里叶变换
我们用 F N F_N FN来表示坐标矩阵,从标准基 R N \mathbb{R}^N RN到傅里叶基 F N \mathcal{F}_N FN的变化。我们也将其称为( N N N点)傅立叶矩阵。
矩阵 N F N \sqrt{N} F_N NFN 也称为( N N N点)离散傅里叶变换,或 DFT。如果 x \boldsymbol{x} x是 R N R^N RN中的向量,则 y = \boldsymbol{y}= y= DFT x \boldsymbol{x} x称为 x \boldsymbol{x} x的DFT系数。 (因此,DFT 系数是 F N \mathcal{F}_N FN 中的坐标,用 N \sqrt{N} N 缩放)。 DFT x \boldsymbol{x} x 有时写为 x ^ \hat{\boldsymbol{x}} x^。
请注意,我们将傅立叶矩阵和 DFT 定义为两个不同的矩阵,一个是另一个的缩放版本。究其原因,在于不同领域有不同的传统。在纯数学中,主要使用傅立叶矩阵,因为正如我们将看到的,它是酉矩阵。在信号处理中,主要使用 DFT 提供的缩放版本。我们通常将 R N \mathbb{R}^N RN中的给定向量写为 x \boldsymbol{x} x,并为其DFT写为 y \boldsymbol{y} y。在应用领域中,傅里叶基向量也称为合成向量,因为它们可以用来“合成”向量 x \boldsymbol{x} x,其权重由傅里叶基中的坐标提供,即
x = y 0 ϕ 0 + y 1 ϕ 1 + ⋯ + y N − 1 ϕ N − 1 . \boldsymbol{x}=y_0 \phi_0+y_1 \phi_1+\cdots+y_{N-1} \phi_{N-1} \text {. } x=y0ϕ0+y1ϕ1+⋯+yN−1ϕN−1.
此方程也称为合成方程。
Python离散傅里叶变换计算并绘制振幅谱
离散傅里叶变换可以将均匀间隔的信号序列变换为需要求和为时域信号的所有正弦波的频率信息。它定义为:
X k = ∑ n = 0 N − 1 x n ⋅ e − i 2 π k n / N = ∑ n = 0 N − 1 x n [ cos ( 2 π k n / N ) − i ⋅ sin ( 2 π k n / N ) ] X_k=\sum_{n=0}^{N-1} x_n \cdot e^{-i 2 \pi k n / N}=\sum_{n=0}^{N-1} x_n[\cos (2 \pi k n / N)-i \cdot \sin (2 \pi k n / N)] Xk=n=0∑N−1xn⋅e−i2πkn/N=n=0∑N−1xn[cos(2πkn/N)−i⋅sin(2πkn/N)]
让我们看看如何使用它。
import matplotlib.pyplot as plt
import numpy as npplt.style.use('seaborn-poster')
%matplotlib inline# sampling rate
sr = 100
# sampling interval
ts = 1.0/sr
t = np.arange(0,1,ts)freq = 1.
x = 3*np.sin(2*np.pi*freq*t)freq = 4
x += np.sin(2*np.pi*freq*t)freq = 7
x += 0.5* np.sin(2*np.pi*freq*t)plt.figure(figsize = (8, 6))
plt.plot(t, x, 'r')
plt.ylabel('Amplitude')plt.show()
编写一个函数 FT(x),它接受一个参数,x - 输入一维实值信号。该函数将计算信号的 DFT 并返回 DFT 值。将此函数应用于我们上面生成的信号并绘制结果。
def FT(x):N = len(x)n = np.arange(N)k = n.reshape((N, 1))e = np.exp(-2j * np.pi * k * n / N)X = np.dot(e, x)return XX = FT(x)N = len(X)
n = np.arange(N)
T = N/sr
freq = n/T plt.figure(figsize = (8, 6))
plt.stem(freq, abs(X), 'b', \markerfmt=" ", basefmt="-b")
plt.xlabel('Freq (Hz)')
plt.ylabel('Amplitude |X(freq)|')
plt.show()
绘制 DFT 结果的前半部分,我们可以看到频率为 1 Hz、4 Hz 和 7 Hz 的 3 个清晰峰值,幅度为 3、1、0.5,符合预期。 这就是我们如何使用离散傅里叶变换将任意信号分解为简单的正弦波来分析它。
数字图像小波分析
小波是具有与傅里叶基不同性质的函数基,因此它们可以用来解决上述的一些缺点。 与傅立叶基相反,小波基不是固定的:存在多种此类基,用于不同的应用。
Python线性代数傅里叶分析和动态系统模拟分析之一
参阅一:计算思维
参阅二:亚图跨际
相关文章:

Python线性代数数字图像和小波分析之二
要点 数学方程:数字信号和傅里叶分析,离散时间滤波器,小波分析Python代码实现及应用变换过程: 读取音频和处理音频波,使用Karplus-强算法制作吉他音频离散傅里叶计算功能和绘制图示结果计算波形傅里叶系数正向和反向&…...

LC.exe”已退出,代码为 -1
尽管网络上已经有许多详尽的说明和资料,但鉴于个人对大量文字的理解有反感,我就写一个更为直观、简洁的方式来呈现我的解决方案。 1.问题图片。 2.删除licenses.licx 3.问题解决...

springboot + jpa + 达梦数据库兼容 Mysql的GenerationType.IDENTITY主键生成策略
导入达梦数据库对hibernate的方言包 <dependency><groupId>com.dameng</groupId><artifactId>DmDialect-for-hibernate5.6</artifactId><version>8.1.2.192</version></dependency>配置文件中添加方言配置和主键生成策略配置…...

Redis优化与应用
Redis性能调优 - Redis的性能调优是一个比较复杂的过程,需要从多个方面进行优化,如内存使用、命令使用等。 - 案例:减少不必要的持久化操作。默认情况下,Redis会执行RDB和AOF两种持久化方式。如果不需要持久化,或者可…...
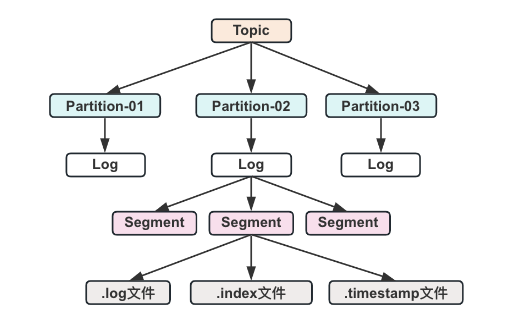
深入了解Kafka的文件存储原理
Kafka简介 Kafka最初由Linkedin公司开发的分布式、分区的、多副本的、多订阅者的消息系统。它提供了类似于JMS的特性,但是在设计实现上完全不同,此外它并不是JMS规范的实现。kafka对消息保存是根据Topic进行归类,发送消息者称为Producer&…...
RabbitMQ 高级
在昨天的练习作业中,我们改造了余额支付功能,在支付成功后利用RabbitMQ通知交易服务,更新业务订单状态为已支付。 但是大家思考一下,如果这里MQ通知失败,支付服务中支付流水显示支付成功,而交易服务中的订单…...

音视频开发之旅——音频基础概念、交叉编译原理和实践(LAME的交叉编译)(Android)
本文主要讲解的是音频基础概念、交叉编译原理和实践(LAME的交叉编译),是基于Android平台,示例代码如下所示: AndroidAudioDemo 音频基础概念 在进行音频开发的之前,了解声学的基础还是很有必要的。 声音…...

直播美颜SDK开发指南:构建个性化的主播美颜工具
本篇文章,小编将带您深入了解如何构建个性化的主播美颜工具,从而为用户提供更优质的直播体验。 一、美颜技术概述 在开始SDK的开发之前,我们首先需要了解美颜技术的基本原理。美颜技术通常包括肤色检测、人脸检测、特征点定位、滤镜处理等步…...

羊大师揭秘,羊奶有哪些好处和不足呢?
羊大师揭秘,羊奶有哪些好处和不足呢? 羊奶的好处主要包括: 营养丰富:羊奶中含有多种人体所需的营养成分,如蛋白质、脂肪、碳水化合物、矿物质和维生素等。尤其是蛋白质含量高,且易于人体吸收利用。 增强免…...

鸿蒙问题之CustomDialog后持久化@state数据崩溃
开发需求:有一个字符串数组,可以通过弹框编辑其中的某个字符串,编辑完成后更新数组并持久化这个数组。 这个需求算是很简单,很常见的需求了。但是,开发过程中却遇到了一个不小的难题。 我的数组内容需要在组件中显示…...

微服务高性能通信技术-gRPC实战落地
在微服务架构中,服务之间的通信是至关重要的。为了实现高性能、低延迟和跨语言的服务间通信,gRPC是一个流行的选择。gRPC是一个开源的、高性能的、通用的RPC(远程过程调用)框架,基于HTTP/2协议和Protocol Buffers序列化…...

洛阳旅游攻略
洛阳旅游攻略 第一天(抵达当天): 1.先将行李放到酒店—2.老城十字街(打车可能会堵车)—3.洛邑古城—4.丽景门(步行) 第二天: 1.早起吃早餐—(打车三十分钟,…...
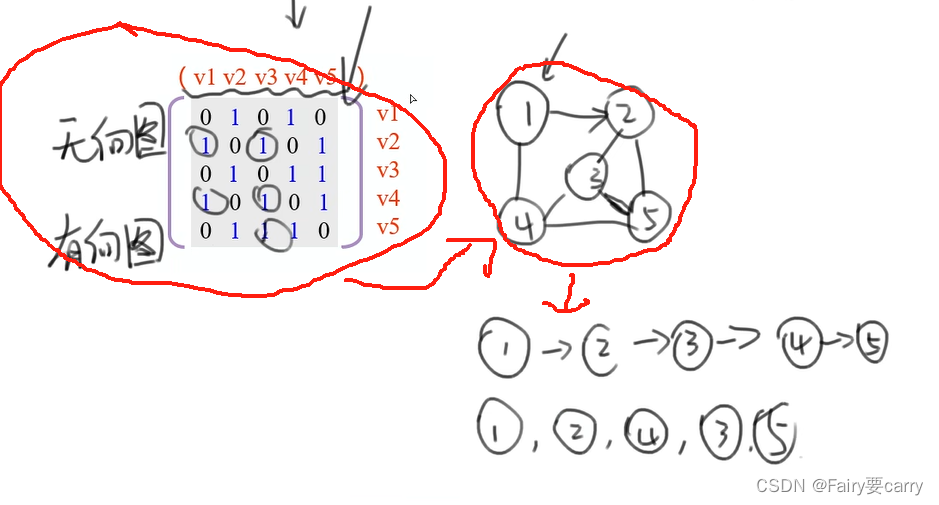
图论例题解析
1.图论基础概念 概念 (注意连通非连通情况,1节点) 无向图: 度是边的两倍(没有入度和出度的概念) 1.完全图: 假设一个图有n个节点,那么任意两个节点都有边则为完全图 2.连通图&…...

图解 TCP 拥塞控制
文章目录 什么是拥塞控制拥塞控制算法慢启动拥塞避免快速恢复 TCP拥塞控制状态机 什么是拥塞控制 拥塞控制是一种 确保网络中的数据包以可持续的速率传输 的机制,避免因为数据包太多而超过网络当前的承载能力,导致网络性能下降,甚至产生大量…...
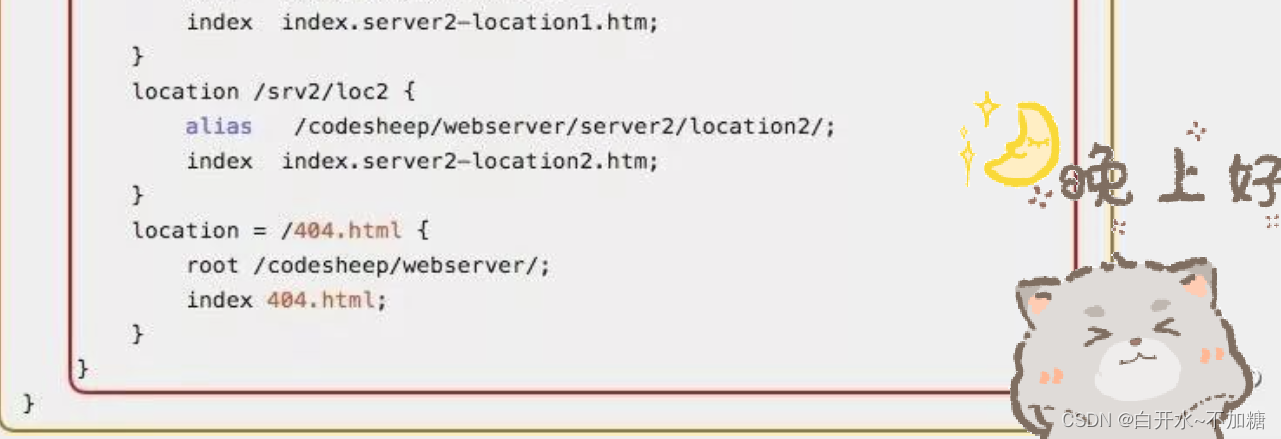
Nginx配置文件的整体结构
一、Nginx配置文件的整体结构 从图中可以看出主要包含以下几大部分内容: 1. 全局块 该部分配置主要影响Nginx全局,通常包括下面几个部分: 配置运行Nginx服务器用户(组) worker process数 Nginx进程PID存放路径 错误…...
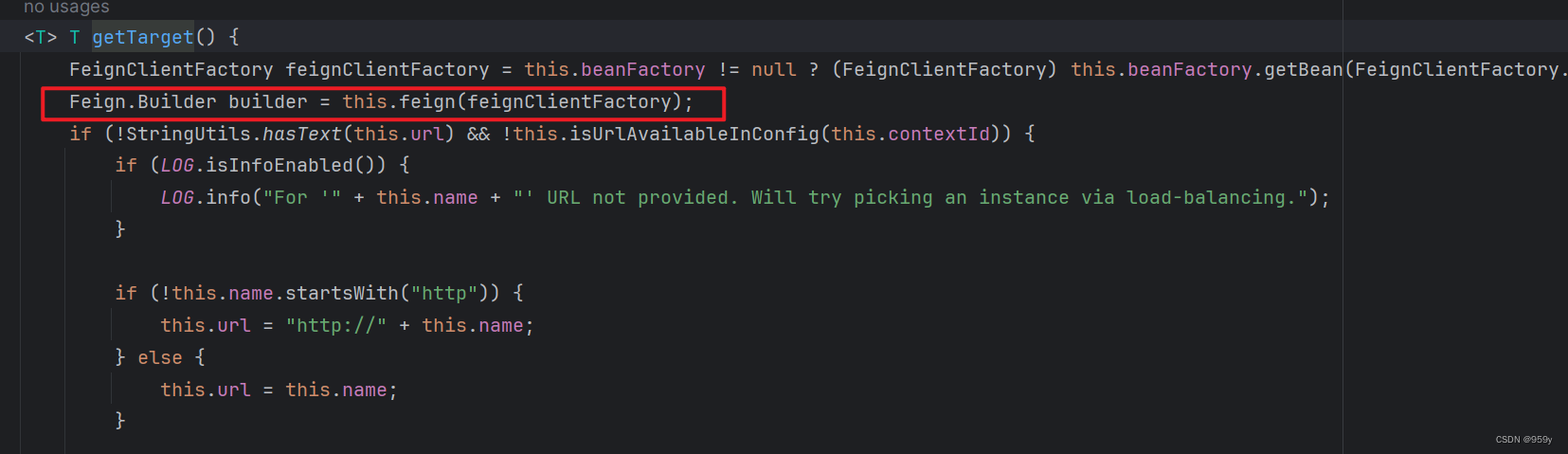
[SpringCloud] OpenFeign核心架构原理 (三)
文章目录 1.SpringCloud是如何整合Feign的1.1 将FeignClient接口注册到Spring中1.2 FeignClientFactoryBean相关 1.SpringCloud是如何整合Feign的 核心组件重新实现, 支持更多的SpringCloud生态的功能。将接口动态代理对象注入到Spring容器中。 1.1 将FeignClient接口注册到S…...

elementUI Table组件点击取当前行索引
在使用element UI Table组件时,需要点击取当前行索引,并删除当前行,看了element UI 文档好象没有这个的,仔细看下发现当前行索引是在scope里的$.index里。 element UI文档:https://www.uihtm.com/element/#/zh-CN/comp…...

组基轨迹建模 GBTM的介绍与实现(Stata 或 R)
基本介绍 组基轨迹建模(Group-Based Trajectory Modeling,GBTM)(旧名称:Semiparametric mixture model) 历史:由DANIELS.NAGIN提出,发表文献《Analyzing Developmental Trajectori…...

解决前端性能问题:如何优化大量数据渲染和复杂交互?
✨✨祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天开心!✨✨ 🎈🎈作者主页: 喔的嘛呀🎈🎈 目录 引言 一、分页加载数据 二、虚拟滚动 三、懒加载 四、数据缓存 五、减少重绘和回流 …...

【Vue3】深入理解Vue中的ref属性
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
