算法D38| 动态规划1 | 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
理论基础
无论大家之前对动态规划学到什么程度,一定要先看 我讲的 动态规划理论基础。
如果没做过动态规划的题目,看我讲的理论基础,会有感觉 是不是简单题想复杂了?
其实并没有,我讲的理论基础内容,在动规章节所有题目都有运用,所以很重要!
如果做过动态规划题目的录友,看我的理论基础 就会感同身受了。
代码随想录
视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩_bilibili
509. 斐波那契数
很简单的动规入门题,但简单题使用来掌握方法论的,还是要有动规五部曲来分析。
代码随想录
视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili
Python:
太经典了。
class Solution:def fib(self, n: int) -> int:a = 0b = 1for _ in range(n):a, b = b, a+breturn aC++:
cpp没有python同时赋值的操作,注意一下语法实现。
class Solution {
public:int fib(int n) {int a = 0;int b = 1;int tmp;for (int i=0; i<n; i++) {tmp = b;b = a+b;a = tmp; }return a;}
};70. 爬楼梯
本题大家先自己想一想, 之后会发现,和 斐波那契数 有点关系。
代码随想录
视频:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目_哔哩哔哩_bilibili
Python:
和斐波那契思路基本一致,递归是会超时的,注意内存和时间的优化,O(n)最优。
class Solution:def climbStairs(self, n: int) -> int:if n<=2: return na, b = 1, 2for _ in range(2, n+1):a, b = b, a+breturn aC++:
return b可以保证在n=45时不溢出,return a在n=45时会溢出。
class Solution {
public:int climbStairs(int n) {if (n<=2) return n;int a = 1;int b = 2;for (int i=2; i<n; i++) {int tmp = a+b;a = b;b = tmp;}return b;}
};746. 使用最小花费爬楼梯
这道题目力扣改了题目描述了,现在的题目描述清晰很多,相当于明确说 第一步是不用花费的。
更改题目描述之后,相当于是 文章中 「拓展」的解法
代码随想录
视频讲解:动态规划开更了!| LeetCode:746. 使用最小花费爬楼梯_哔哩哔哩_bilibili
Python:
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:cost.append(0)a = b = 0for c in cost:if a>b:a, b = b, b+celse:a, b = b, a+creturn bC++:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int a = 0;int b = 0;int tmp;cost.push_back(0);for (int c:cost) {tmp = b;if (a>b) {b += c;} else {b = a+c;}a = tmp;}return b;}
};相关文章:

算法D38| 动态规划1 | 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
理论基础 无论大家之前对动态规划学到什么程度,一定要先看 我讲的 动态规划理论基础。 如果没做过动态规划的题目,看我讲的理论基础,会有感觉 是不是简单题想复杂了? 其实并没有,我讲的理论基础内容,在动…...

Vue教学13:组件的生命周期:掌握组件的每一个关键时刻
大家好,欢迎回到我们的Vue教学系列博客!在前十二篇博客中,我们学习了Vue.js的基础知识、安装Node.js与npm、使用Vue Devtools进行调试、Vue实例与生命周期钩子、数据绑定(单向与双向)、计算属性与侦听器、条件渲染和列…...
mitmproxy代理
文章目录 mitmproxy1. 网络代理2. 安装3. Https请求3.1 启动mitmproxy3.2 获取证书3.3 配置代理3.4 运行测试 4. 请求4.1 读取请求4.2 修改请求4.3 拦截请求 5. 响应5.1 读取响应5.2 修改响应 6. 案例:共享账号6.1 登录bilibili获取cookies6.2 在代理请求中设置cook…...
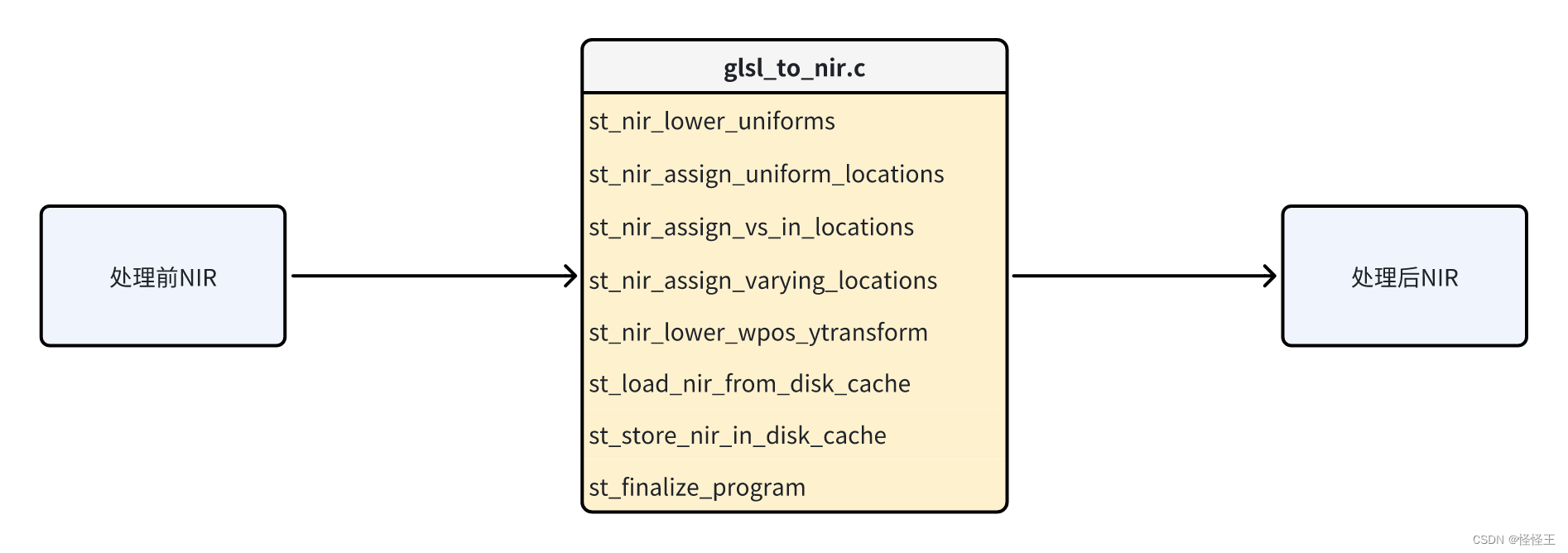
【GPU驱动开发】- mesa编译与链接过程详细分析
前言 不必害怕未知,无需恐惧犯错,做一个Creator! 一、总体框架图 暂时无法在飞书文档外展示此内容 二、Mesa API 处理 OpenGL 函数调用 Mesa API 负责实现 OpenGL 和其他图形 API 的函数接口。Mesa API 表是一个重要的数据结构…...
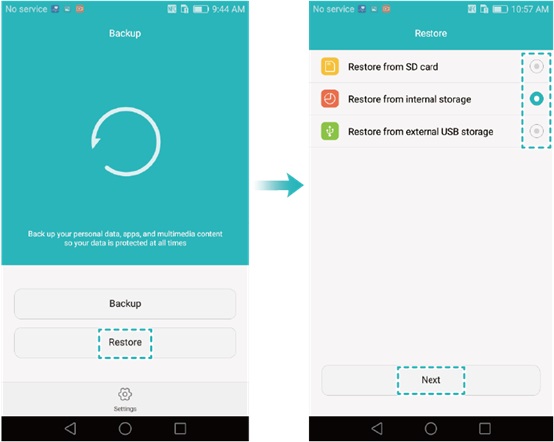
如何恢复已删除的华为手机图片?5 种方式分享
不幸的现实是,华为的珍贵时刻有时会因为意外删除、软件故障或其他不可预见的情况而在眨眼之间消失。在这种情况下,寻求恢复已删除的图片成为个人迫切关心的问题。 本文旨在为用户提供如何从华为恢复已删除图片的实用解决方案。我们将探索五种可行的方法…...
)
通过 python 和 wget 批量下载文件(在Linux/Ubuntu/Debian中测试)
首先创建一个文本文件d.txt, 一行一个链接。 你可以使用简单的 Python 脚本逐行读取文件 (d.txt) 中的链接,并使用 wget 下载文件: import subprocess# File containing download links (replace with your file path) file_path d.txt# Function to …...
)
个人博客系列-后端项目-RBAC角色管理(6)
设计用户表 ## 用户表 class User(models.Model):username models.CharField(max_length255, uniqueTrue, verbose_name"手机号")password models.CharField(max_length255, uniqueFalse, verbose_name"密码")is_vip models.BooleanField(defaultFalse…...
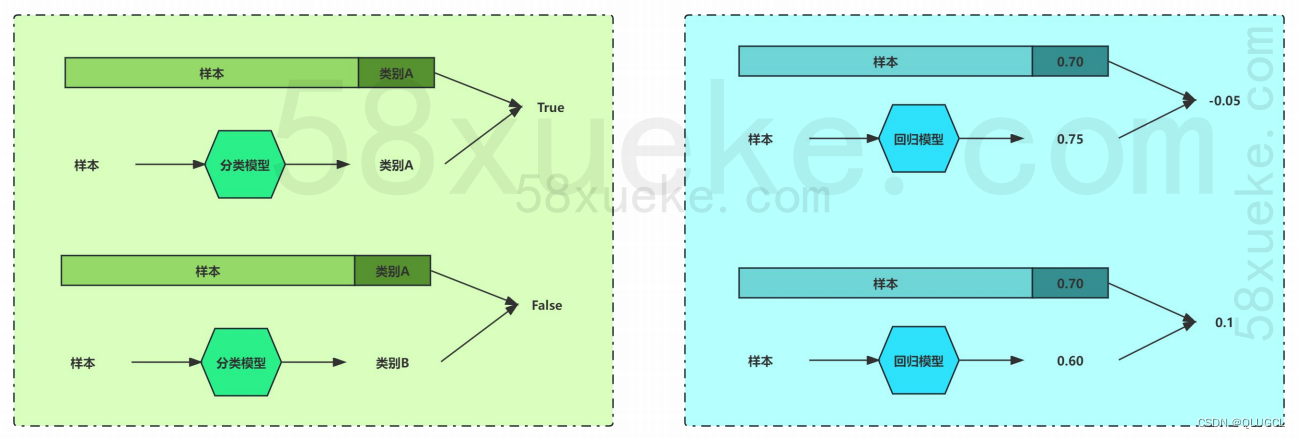
机器学习-启航
文章目录 原理分析机器学习的两种典型任务机器学习分类总结数据机器学习分类解读简单复杂 原理分析 马克思主义哲学-规律篇 规律客观存在,万事万物皆有规律。 机器学习则是多维角度拆解分析复杂事实数据,发现复杂事实背后的规律,然后将规律用…...

驱动调试第014期-变频调速的原理及相关计算公式应用
一、引言 变频调速是一种通过改变电源频率来实现电动机调速的技术。它具有高效、精确、可靠等优点,广泛应用于工业、商业和家用领域。本文将介绍变频调速的基本原理、优点以及应用领域,并通过详细的公式计算过程和图片说明来帮助读者更好地理解。 二、变…...
JavaWeb环境配置 IDE2022版
一、新建一个javaweb文件 文件名可以自己随意改 二、给建立的项目添加框架支持 勾选Web Application,点击确定 建立成功界面,会生成一个新的web文件夹 三、配置tomcat 1、两种打开配置文件方式: 第一种 第二种 2、打开后,点击号…...
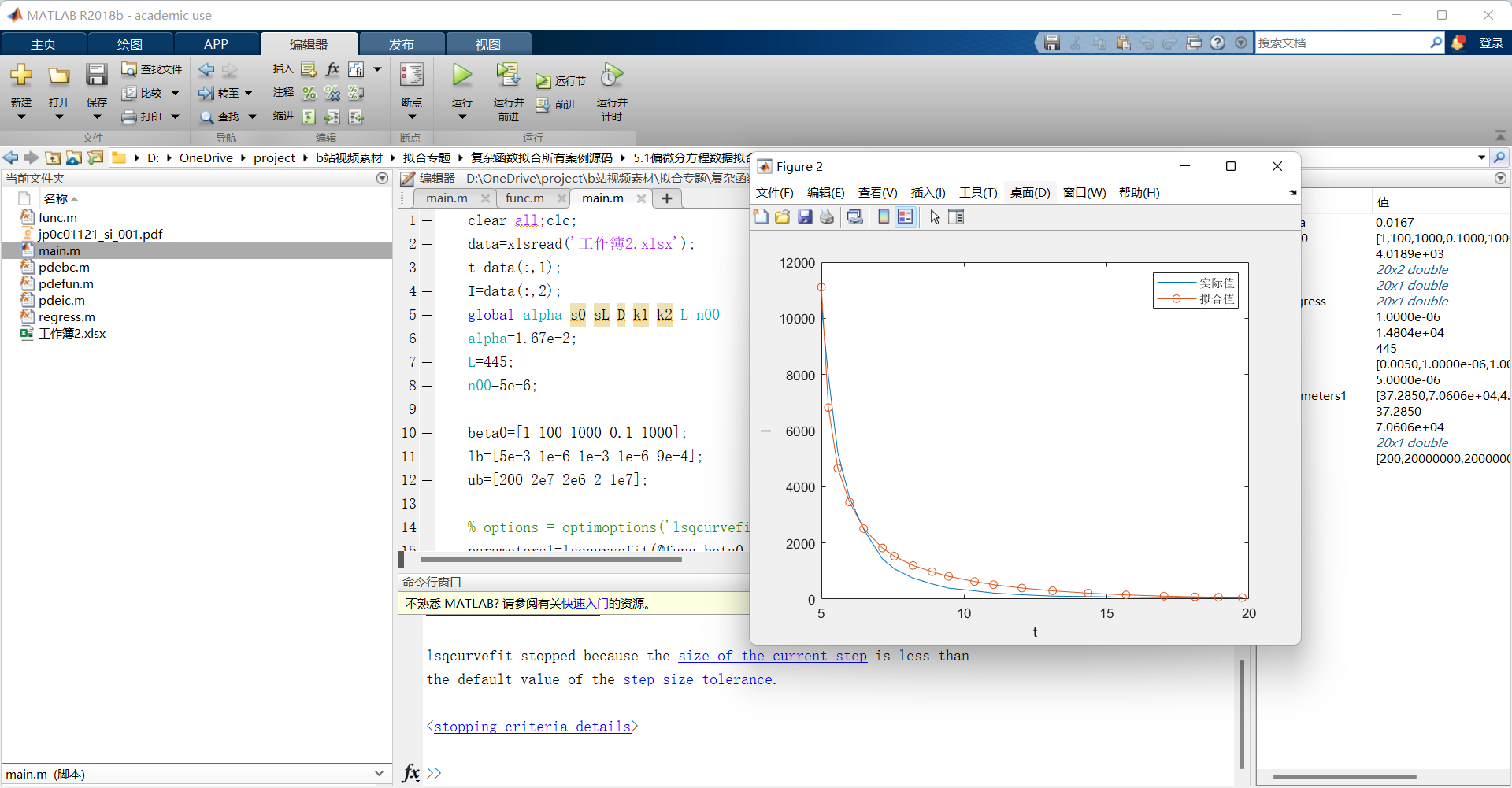
Matlab偏微分方程拟合 | 完整源码 | 视频教程
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法,并提供所有案例完整源码;2.…...
)
什么是yocto基本组件(bitbake,recipes,classes,configuration,layer)
文章目录 1基本组件1.1 bitbake1.2 Recipes1.3 Classes1.4 Configurations2 层的理解2.1 层结构2.2 nxp yocto示例2.3 ti yocto示例1基本组件 1.1 bitbake bitbake,是OpenEmbedded构建系统的核心工具,负责解析元数据,从中生成任务列表,然后执行这些任务。bitbake是一个通…...
electron 程序与安装包图标放大与制作
原因 electron-builder 在打包时需要最小支持到256x256像素的icon图标。原有历史图标都太小了。需要尝试将图标放大。 工具 convertio.co/zh/ico-png/ 在线ico转png网站 https://github.com/upscayl/upscayl 图片放大工具 csdn下载 greenfish-icon-editor-pro.en.softonic.c…...
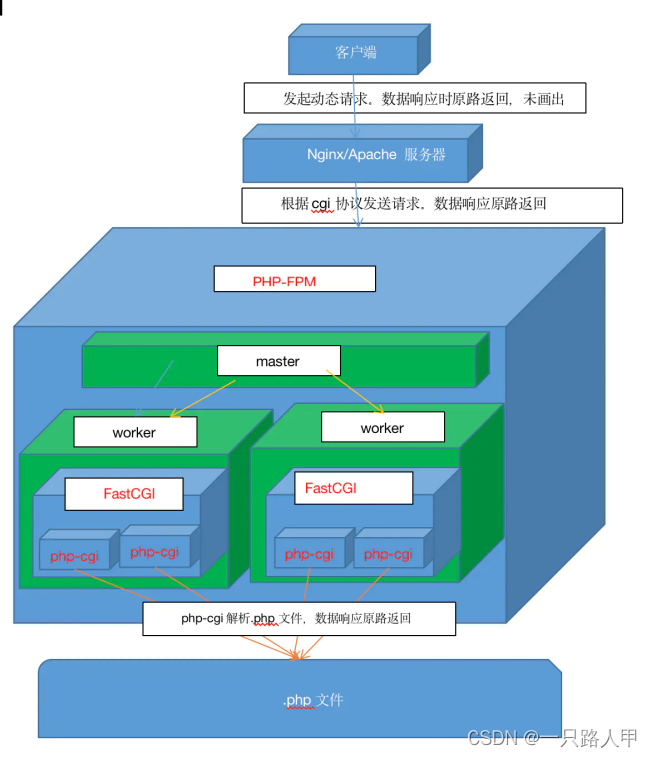
nginx,php-fpm
一,Nginx是异步非阻塞多进程,io多路复用 1、master进程:管理进程 master进程主要用来管理worker进程,具体包括如下4个主要功能: (1)接收来自外界的信号。 (2)向各worker进…...

网络编程(3/4)
广播 #include<myhead.h>int main(int argc, const char *argv[]) {//1、创建套接字int sfd socket(AF_INET, SOCK_DGRAM, 0);if(sfd -1){perror("socket error");return -1;}//2、将套接字设置成允许广播int broadcast 1;if(setsockopt(sfd, SOL_SOC…...

vue computed计算属性
模板中的表达式虽然方便,但也只能用来做简单的操作;如果在模板中写太多逻辑,会让模板变得臃肿,难以维护;因此我们推荐使用计算属性来描述依赖响应式状态的复杂逻辑 1. 选项式 API 中,可以提供computed选项来…...

智慧路灯物联网管理平台及应用
资产维护 路灯物联网涉及的设备数量大,种类多,生产厂家和批次多样化,对路灯物联网的资产维护是一项艰巨的工作。资产维护管理能够有效的管理路灯资产及各类传感设备资产信息,实现精细化管理。平台提供了对集中控制器、各感测设备节点控制器等设备的信息进行管理,包括录入…...
基于OpenCV的图形分析辨认02
目录 一、前言 二、实验目的 三、实验内容 四、实验过程 一、前言 编程语言:Python,编程软件:vscode或pycharm,必备的第三方库:OpenCV,numpy,matplotlib,os等等。 关于OpenCV&…...

python基础——基础语法
文章目录 一、基础知识1、字面量2、常用值类型3、注释4、输入输出5、数据类型转换6、其他 二、字符串拓展1、字符串定义2、字符串拼接3、字符串格式化4、格式化精度控制 三、条件/循环语句1、if2、while3、for循环 四、函数1、函数定义2、函数说明文档3、global关键字 五、数据…...
vue3 vue-i18n 多语言
1. 安装 npm install vue-i18n -s 2. 引入main.js import { createI18n } from vue-i18n import messages from ./i18n/index const i18n createI18n({legacy: false,locale: Cookies.get(language) || en_us, // set localefallbackLocale: en_us, // set fallback local…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
