【动态规划】【数论】【区间合并】3041. 修改数组后最大化数组中的连续元素数目
作者推荐
视频算法专题
本文涉及知识点
动态规划汇总
数论 区间合并
LeetCode3041. 修改数组后最大化数组中的连续元素数目
给你一个下标从 0 开始只包含 正 整数的数组 nums 。
一开始,你可以将数组中 任意数量 元素增加 至多 1 。
修改后,你可以从最终数组中选择 一个或者更多 元素,并确保这些元素升序排序后是 连续 的。比方说,[3, 4, 5] 是连续的,但是 [3, 4, 6] 和 [1, 1, 2, 3] 不是连续的。
请你返回 最多 可以选出的元素数目。
示例 1:
输入:nums = [2,1,5,1,1]
输出:3
解释:我们将下标 0 和 3 处的元素增加 1 ,得到结果数组 nums = [3,1,5,2,1] 。
我们选择元素 [3,1,5,2,1] 并将它们排序得到 [1,2,3] ,是连续元素。
最多可以得到 3 个连续元素。
示例 2:
输入:nums = [1,4,7,10]
输出:1
解释:我们可以选择的最多元素数目是 1 。
提示:
1 <= nums.length <= 105
1 <= nums[i] <= 106
数论
先排序。
合并方式一:如果[left,r]中的数至少出现1次,则可以通过将所有数+1,从[left,r]转化成[left+1,r+1]。
合并方式二:如果[left,r]中的数至少出现1次,且至少一个数x出现两次。则可以将[left,r]转化成[left,r+1]。x → \rightarrow →x+1,x+1 → \rightarrow →x+2 ⋯ \cdots ⋯ r → \rightarrow → r+1。 如: {1,1,2,3} → \rightarrow → {1,2,3,4}
如果 [l1,r1] 和[l2,r2] 是合法区间,r1+2= l2
方式一合并后,变成[l1+1,r2] ,由于缺少l1,合并后无法合并更小的区间。
方式二合并后,变成[l1,r2],可以继续合并更小的区间。
合并后的重复数字以[l2,r2]为准,[l1,r1]无论有多少个数字多不能变成r1+2,所以不会影响新区间。
我们枚举方式二的开始,如果 [l1,r1] 和[l2,r2] 能通过方式二合并,则无需枚举[l2,r2]。
代码
核心代码
template<class ELE>
void MaxSelf(ELE* seft, const ELE& other)
{*seft = max(*seft, other);
}#define MacEnumMask(mask,maskMax) for (int mask = maskMax; mask; mask = (mask - 1) & maskMax) class Solution {
public:int maxSelectedElements(vector<int>& nums) {sort(nums.begin(), nums.end());vector<tuple<int, int, bool>> vLRTow;int left = 0;bool bRepeat = false;for (int i = 1; i < nums.size(); i++){if (nums[i] == nums[i - 1]){bRepeat = true;}else if (nums[i] != nums[i - 1] + 1){vLRTow.emplace_back(nums[left], nums[i - 1], bRepeat);left = i;bRepeat = false;}}vLRTow.emplace_back(nums[left], nums.back(), bRepeat);std::unordered_map<int, int> mEndToLen;for (const auto& [left, r, tmp] : vLRTow){mEndToLen[r] = r - left + 1;}vector<tuple<int, int, bool>> vLRTow2;for (int i = 0; i < vLRTow.size(); ){ vLRTow2.emplace_back(vLRTow[i]);i++;for ( ; i < vLRTow.size(); i ++){if (get<2>(vLRTow2.back()) && (get<1>(vLRTow2.back()) + 2 == get<0>(vLRTow[i]))){get<2>(vLRTow2.back()) = get<2>(vLRTow[i]);get<1>(vLRTow2.back()) = get<1>(vLRTow[i]);}else{break;}} } int iRet = 0;for (int i = 0 ; i < vLRTow2.size();i++){const auto& [left, r, bReapt] = vLRTow2[i];int pre = mEndToLen.count(left-2 )? mEndToLen[left-2] :0;MaxSelf(&iRet, pre + r - left + 1 + bReapt);}return iRet;}
};
测试用例
int main()
{vector<int> nums;{Solution sln;nums = { 16,1,6,14,5,10,16,3,3,7,12,18,6,11,10,10,9,16 };auto res = sln.maxSelectedElements(nums);Assert(13, res);}{Solution sln;nums = { 9, 8, 8, 5, 15, 9, 12, 5, 1, 3, 7, 18, 10 };auto res = sln.maxSelectedElements(nums);Assert(9, res);}{Solution sln;nums = { 8,13,18,10,16,19,11,17,15,18,9,12,15,8,9,14,7 };auto res = sln.maxSelectedElements(nums);Assert(14, res);}{Solution sln;nums = { 12, 11, 8, 7, 2, 10, 18, 12 };auto res = sln.maxSelectedElements(nums);Assert(6, res);}{Solution sln;nums = { 8,10,6,12,9,12,2,3,13,19,11,18,10,16 };auto res = sln.maxSelectedElements(nums);Assert(8, res);}{Solution sln;nums = { 2,1,4,1,1 };auto res = sln.maxSelectedElements(nums);Assert(4, res);}{Solution sln;nums = { 2,1,5,1,1 };auto res = sln.maxSelectedElements(nums);Assert(3, res);}
}
优化代码:简洁
template<class ELE>
void MaxSelf(ELE* seft, const ELE& other)
{*seft = max(*seft, other);
}#define MacEnumMask(mask,maskMax) for (int mask = maskMax; mask; mask = (mask - 1) & maskMax) class Solution {
public:int maxSelectedElements(vector<int>& nums) {sort(nums.begin(), nums.end());vector<tuple<int, int, bool>> vLRTow;int left = 0;bool bRepeat = false;for (int i = 1; i < nums.size(); i++){if (nums[i] == nums[i - 1]){bRepeat = true;}else if (nums[i] != nums[i - 1] + 1){vLRTow.emplace_back(nums[left], nums[i - 1], bRepeat);left = i;bRepeat = false;}}vLRTow.emplace_back(nums[left], nums.back(), bRepeat);int iRet = 0;for (int i = 0; i < vLRTow.size(); ){ int j = i + 1;int right = get<1>(vLRTow[i]) + get<2>(vLRTow[i]);for (; j < vLRTow.size(); j++){if (get<2>(vLRTow[j-1]) && (get<1>(vLRTow[j - 1]) + 2 == get<0>(vLRTow[j]))){right = get<1>(vLRTow[j]) + get<2>(vLRTow[j]);}else{break;}} int pre = ((i > 0) && (get<1>(vLRTow[i - 1]) + 2 == get<0>(vLRTow[i]))) ? (get<1>(vLRTow[i - 1]) - get<0>(vLRTow[i - 1]) + 1) : 0;MaxSelf(&iRet, right - get<0>(vLRTow[i])+1 + pre );i = j;}return iRet;}
};
动态规划
动态规划的状态
dp[x]表示以x结尾的最长连续数量。
动态规划的初始值
无,或者或全部为0。
动态规划的状态方程
{ d p [ x + 1 ] = m a x ( d p [ x + 1 ] , d p [ x ] + 1 ) x 加一 d p [ x ] = m a x ( d p [ x ] , d p [ x − 1 ] + 1 ) x 不变 \begin{cases} dp[x+1] = max(dp[x+1],dp[x]+1) & x加一 \\ dp[x] = max(dp[x],dp[x-1]+1) & x不变\\ \end{cases} {dp[x+1]=max(dp[x+1],dp[x]+1)dp[x]=max(dp[x],dp[x−1]+1)x加一x不变
动态规划的填表顺序
x从小到大。先处理x+1,再处理x。否则{1}的结果是dp[1]=1,dp[2]=2。
代码
template<class ELE>
void MaxSelf(ELE* seft, const ELE& other)
{*seft = max(*seft, other);
}class Solution {
public:int maxSelectedElements(vector<int>& nums) {sort(nums.begin(), nums.end());unordered_map<int, int> dp;for (const auto& n : nums){MaxSelf(&dp[n + 1], dp[n] + 1);MaxSelf(&dp[n ], dp[n - 1] + 1);}int iRet = 0;for (const auto& [tmp, len] : dp){MaxSelf(&iRet, len);}return iRet;}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【数论】【区间合并】3041. 修改数组后最大化数组中的连续元素数目
作者推荐 视频算法专题 本文涉及知识点 动态规划汇总 数论 区间合并 LeetCode3041. 修改数组后最大化数组中的连续元素数目 给你一个下标从 0 开始只包含 正 整数的数组 nums 。 一开始,你可以将数组中 任意数量 元素增加 至多 1 。 修改后,你可以从…...

字节后端实习 一面凉经
心脏和字节永远都在跳动 深圳还有没有大厂招后端日常实习生啊,求捞~(boss小公司也不理我) 很纠结要不要干脆直接面暑期实习,又怕因为没有后端实习经历,面不到大厂实习。死锁了...

倒计时37天
复习1001. 马走日问题: 1.P1002 [NOIP2002 普及组] 过河卒 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) //日常碎碎念:谁懂啊,dev突然不能用了,也不知道是哪里出了问题下了五六次都不能用,,,找远程安…...
【计算机考研】考408,还是不考408性价比高?
首先综合考虑,如果其他科目并不是很优秀,需要我们花一定的时间去复习,408的性价比就不高,各个科目的时间互相挤压,如果备考时间不充裕,考虑其他专业课也未尝不可。 复习408本来就是费力不讨好的事情 不同…...

测试入门篇
测试: 这里写目录标题 测试:基础概念:BUG:创建一个合理的bug:bug 的级别:跟开发争执如何解决: 测试用例:编写测试用例的万能公式:案例: 登录功能的测试:设计测试用例的方法: 进阶篇(主要介绍测试方法):自动化测试:自动化测试的分类:selenium( web 自动化测试工具 )环境部署:什么…...

b站小土堆pytorch学习记录—— P25-P26 网络模型的使用和修改、保存和读取
文章目录 一、修改1.方法2.代码 二、保存和读取1.方法2.代码(1)保存(2)加载 3.陷阱 一、修改 1.方法 add_module(name: str, module: Module) -> None name 是要添加的子模块的名称。 module 是要添加的子模块。 调用 add_m…...
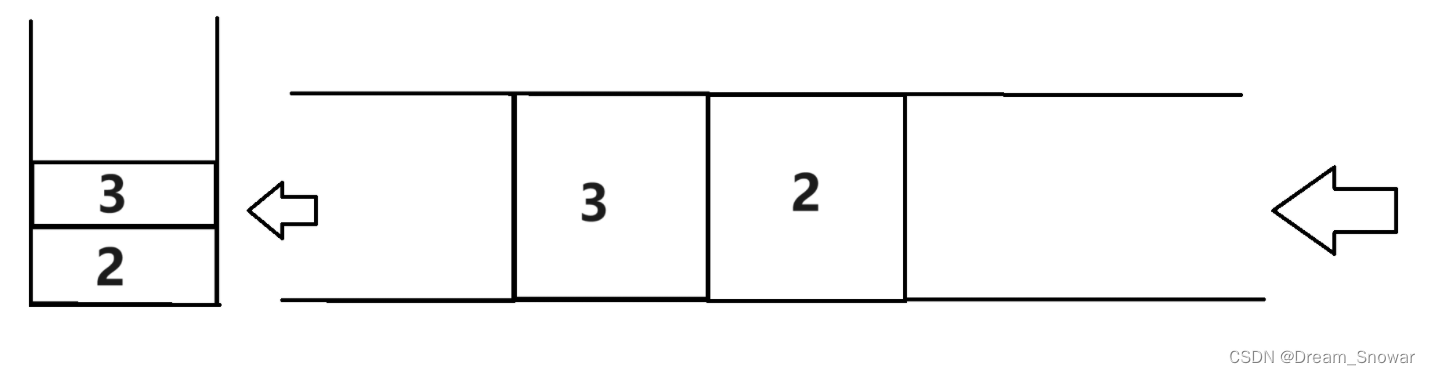
[数据结构]OJ用队列实现栈
225. 用队列实现栈 - 力扣(LeetCode) 官方题解:https://leetcode.cn/problems/implement-stack-using-queues/solutions/432204/yong-dui-lie-shi-xian-zhan-by-leetcode-solution/ 首先我们要知道 栈是一种后进先出的数据结构,…...

「优选算法刷题」:最长回文子串
一、题目 给你一个字符串 s,找到 s 中最长的回文子串。 如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。 示例 1: 输入:s "babad" 输出:"bab" 解释:"aba"…...
Java项目:41 springboot大学生入学审核系统的设计与实现010
作者主页:舒克日记 简介:Java领域优质创作者、Java项目、学习资料、技术互助 文中获取源码 项目介绍 本大学生入学审核系统管理员和学生。 管理员功能有个人中心,学生管理,学籍信息管理,入学办理管理等。 学生功能有…...

【数据结构与算法】常见排序算法(Sorting Algorithm)
文章目录 相关概念1. 冒泡排序(Bubble Sort)2. 直接插入排序(Insertion Sort)3. 希尔排序(Shell Sort)4. 直接选择排序(Selection Sort)5. 堆排序(Heap Sort)…...

Unity3D学习之XLua实践——背包系统
文章目录 1 前言2 新建工程导入必要资源2.1 AB包设置2.2 C# 脚本2.3 VSCode 的环境搭建 3 面板拼凑3.1 主面板拼凑3.2 背包面板拼凑3.3 格子复合组件拼凑3.4 常用类别名准备3.5 数据准备3.5.1 图集准备3.5.2 json3.5.3 打AB包 4 Lua读取json表及准备玩家数据5 主面板逻辑6 背包…...

前端技术研究越深入,越觉得技术不是决定录用唯一条件。
一、拒绝抬杠 我说技能不是唯一条件,不是说技能不重要,招聘前端条件是1X,其中1是技能,X是其他条件。 如果X条件很优秀,1这个条件可以降格为0.8、0.5,甚至更低。 有人就抬杠,那为啥不招聘清洁工来干前端&…...

vue组件的重新渲染的问题
目录 1.方式1 2.方式2 1.方式1 修改组件上的key属性 Vue是通过diffing算法比较虚拟DOM和真实DOM,来判断新旧 DOM 的变化。key是虚拟DOM对象的标识,在更新显示时key表示着DOM的唯一性。 DOM是否变化的核心是通过判断新旧DOM的key值是否变化,…...
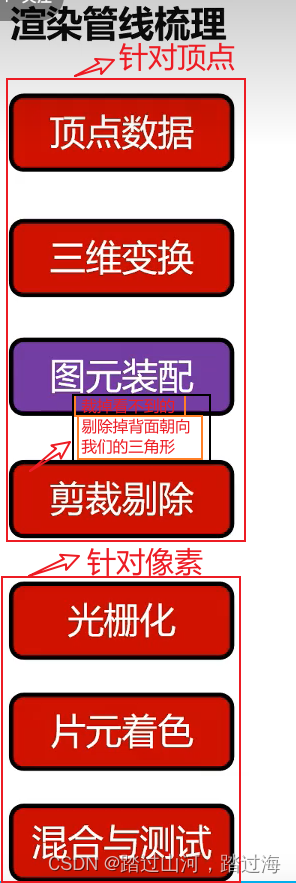
opengl 学习(二)-----你好,三角形
你好,三角形 分类demo效果解析 分类 opengl c demo #include "glad/glad.h" #include "glfw3.h" #include <iostream> #include <cmath> #include <vector>using namespace std;/** * 在学习此节之前,建议将这…...

mongodb4.2升级到5.0版本,升级到6.0版本, 升级到7.0版本案例
今天一客户想把自己当前使用的mongodb数据库4.2版本升级到7.0版本。难道mongodb能直接跳跃升级吗? 经过几经查找资料,貌似真不行呀。确定升级流程如下: 还得从mongo4.2升级到5.0。其次再从5.0升级到6.0。最后再从6.0升级到7.0。 开始升级之前将数据进行备份 这一步…...

CPU处理器模式与异常
ARM架构中的Exception Level(EL) 在ARM架构中,Exception Level(EL)是一个关键概念,它表示了处理器当前处理异常或中断的层次。ARMv8-A架构定义了四个Exception Levels:EL0、EL1、EL2和EL3&…...

Day 53 |● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和
1143.最长公共子序列 class Solution { public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size()1,vector<int>(text2.size()1,0));int res 0;for(int i 1; i < text1.size(); i){for(int j 1; j <…...

ant-desgin charts双轴图DualAxes,柱状图无法立即显示,并且只有在调整页面大小(放大或缩小)后才开始显示
摘要 双轴图表中,柱状图无法立即显示,并且只有在调整页面大小(放大或缩小)后才开始显示 官方示例代码 在直接复制,替换为个人数据时,出现柱状图无法显示问题 const config {data: [data, data],xFiel…...
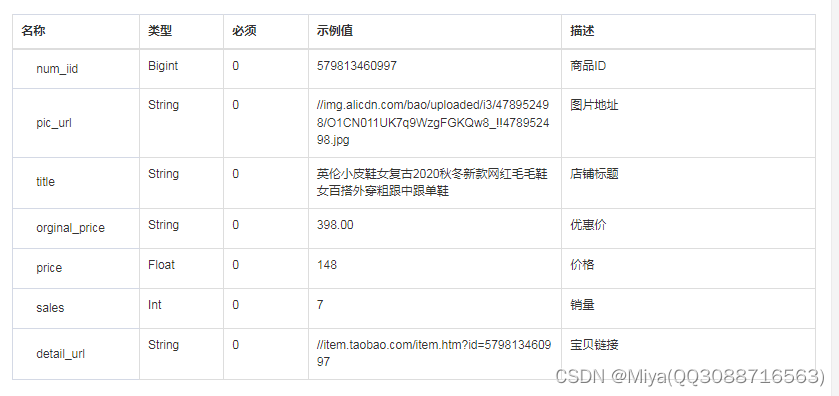
获取别人店铺的所有商品API接口
使用淘宝淘口令接口的步骤通常包括: 注册成为淘宝开放平台的开发者:在淘宝开放平台网站上注册账号并完成认证。 创建应用以获取API密钥:在您的开发者控制台中创建一个应用,并获取用于API调用的密钥,如Client ID和Clie…...

成都正信:亲戚借了钱一直不还怎么委婉的说
在中国传统文化中,亲情关系往往被视为最为重要和敏感的部分。当亲戚间发生借贷时,若出现拖欠不还的情形,处理起来尤为棘手。面对这样的尴尬局面,采取委婉而有效的沟通方式至关重要。 张华最近就遇到了这样的困扰。他的表弟去年因急…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
