代码学习记录10
随想录日记part10
t i m e : time: time: 2024.03.03
主要内容:今天的主要内容是深入了解数据结构中栈和队列,并通过三个 l e e t c o d e leetcode leetcode 题目深化认识。
- 20. 有效的括号
- 1047. 删除字符串中的所有相邻重复项
- 150. 逆波兰表达式求值
Topic1有效的括号
题目:
给定一个只包括 ′ ( ′ , ′ ) ′ , ′ ′ , ′ ′ , ′ [ ′ , ′ ] ′ '(',')','{','}','[',']' ′(′,′)′,′′,′′,′[′,′]′ 的字符串 s s s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例:
输入: s = " ( ) [ ] " s = "()[]{}" s="()[]"
输出: t r u e true true
思路: 括号匹配是使用栈解决的经典问题
先来分析一下 这里有三种不匹配的情况:
1.字符串里左方向的括号多余
2.括号没有多余,但是括号的类型没有匹配上
3.字符串里右方向的括号多余
其 java代码的实现与解释如下:
class Solution {public boolean isValid(String s) {//建立堆栈Stack<Character> stack = new Stack<>();char ch;//如果s的长度不是偶数则无法匹配if(s.length()%2!=0)return false;for(int i=0;i<s.length();i++){ch=s.charAt(i);if(ch=='('){stack.push(')');}else if(ch=='{'){stack.push('}');}else if(ch=='['){stack.push(']');}else if(stack.isEmpty() || stack.peek()!=ch){return false;}else{stack.pop();}}return stack.isEmpty();}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
Topic2删除字符串中的所有相邻重复项
题目:
给出由小写字母组成的字符串 S S S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。在 S S S 上反复执行重复项删除操作,直到无法继续删除。在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
输入: " a b b a c a " "abbaca" "abbaca"
输出: " c a " "ca" "ca"
解释: 例如,在 " a b b a c a " "abbaca" "abbaca" 中,我们可以删除 " b b " "bb" "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 " a a c a " "aaca" "aaca",其中又只有 " a a " "aa" "aa" 可以执行重复项删除操作,所以最后的字符串为 " c a " "ca" "ca"。
思路:
本题也是用栈来解决的经典题目,如下图:
其 java代码的实现与解释如下:
class Solution {public String removeDuplicates(String s) {//建立堆栈Stack<Character> stack = new Stack<>();char ch;for(int i=0;i<s.length();i++){ch=s.charAt(i);if(stack.isEmpty()==true){stack.push(ch);}else{if(ch==stack.peek())stack.pop();else{stack.push(ch);}}}String te="";while(stack.isEmpty()!=true){te=stack.pop()+te;}return te;}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1),返回值不计空间复杂度
Topic3逆波兰表达式求值
题目:
给你一个字符串数组 t o k e n s tokens tokens ,表示一个根据逆波兰表示法表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
示例:
输入: t o k e n s = [ " 2 " , " 1 " , " + " , " 3 " , " ∗ " ] tokens = ["2","1","+","3","*"] tokens=["2","1","+","3","∗"]
输出: 该算式转化为常见的中缀算术表达式为: ( ( 2 + 1 ) ∗ 3 ) = 9 ((2 + 1) * 3) = 9 ((2+1)∗3)=9
思路:
用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中
)
java实现的代码如下:
cclass Solution {public int evalRPN(String[] tokens) {//建立堆栈Stack<Integer> stack = new Stack<>();for(String s:tokens){if("+".equals(s))stack.push(stack.pop()+stack.pop());else if("-".equals(s))stack.push(-stack.pop()+stack.pop());else if("*".equals(s))stack.push(stack.pop()*stack.pop());else if("/".equals(s)){int temp1 = stack.pop();int temp2 = stack.pop();stack.push(temp2 / temp1);}else stack.push(Integer.valueOf(s));} return stack.pop();}
}
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
相关文章:

代码学习记录10
随想录日记part10 t i m e : time: time: 2024.03.03 主要内容:今天的主要内容是深入了解数据结构中栈和队列,并通过三个 l e e t c o d e leetcode leetcode 题目深化认识。 20. 有效的括号1047. 删除字符串中的所有…...
java——2024-03-03
String类的对象能被修改吗?如果不能需要用什么修改?StringBuilder和StringBuffer的区别?equals和区别谈谈对面向对象的理解重载和重写的区别说一下ArrayList,LinkedList底层实现以及区别什么是哈希冲突?hashMap和conCu…...
Ubuntu安装conda以后,给jupyter安装C++内核
前言 大家都知道,jupyter notebook 可以支持python环境,可以在不断点调试的情况下,打印出当前结果,如果代码错了也不影响前面的内容。于是我就想有没有C环境的,结果还真有。 参考文章: 【分享】Ubuntu安装…...
)
【谈判】核心思想(抓大放小)
谈判交换(抓大放小) 一、明确目的 事:must: 非要不可,才会签字 want: 有很好, give: 放掉 三者,会变化 二、明确对象 人:我跟谁谈? 时: 国际形势、国家的政策、他的心…...
)
洛谷P5908 猫猫和企鹅 做题反思(2024.3.7)
猫猫和企鹅 题目传送门 题目描述 王国里有 n n n 个居住区,它们之间有 n − 1 n-1 n−1 条道路相连,并且保证从每个居住区出发都可以到达任何一个居住区,并且每条道路的长度都为 1 1 1。 除 1 1 1 号居住区外,每个居住区住…...
常见的验证码
一、短信验证码 前端: 用户填写手机号,点击按钮发送请求用户短信得到验证码后,用户填写表单提交 form 表单,进行验证 后台: 随机生成几位验证码并将生成时间、手机号、验证码存储起来,可以存到session、…...

11. C语言标准函数库
C语言制定了一组使用方式通用的函数,称为C语言标准函数库,用于实现编程常用功能,标准函数库由编译器系统提供,并按功能分类存储在不同源代码文件中,调用标准库内函数时需要首先使用 #include 连接对应的源代码文件。 【…...

2016年认证杯SPSSPRO杯数学建模C题(第一阶段)如何有效的抑制校园霸凌事件的发生解题全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 C题 如何有效的抑制校园霸凌事件的发生 原题再现: 近年来,我国发生的多起校园霸凌事件在媒体的报道下引发了许多国人的关注。霸凌事件对学生身体和精神上的影响是极为严重而长远的,因此对于这些情况我们应该…...

设计模式-抽象工厂模式实践案例
抽象工厂模式(Abstract Factory Pattern)是一种创建型设计模式,它提供了一个接口,用于创建一系列相关或相互依赖的对象,而无需指定它们具体的类。抽象工厂模式是围绕一个超级工厂创建其他工厂的模式。该模式的实现涉及…...

用readproc函数读取进程的状态
概要: 本篇演示用readproc函数读取进程的状态 libprocps库的安装参考笔者的文章readproc.h-CSDN博客 演示所用的系统是Ubuntu22.04 一、代码 #include<stdio.h> #include<stdlib.h> #include<proc/readproc.h> int main() {struct PROCTAB *…...
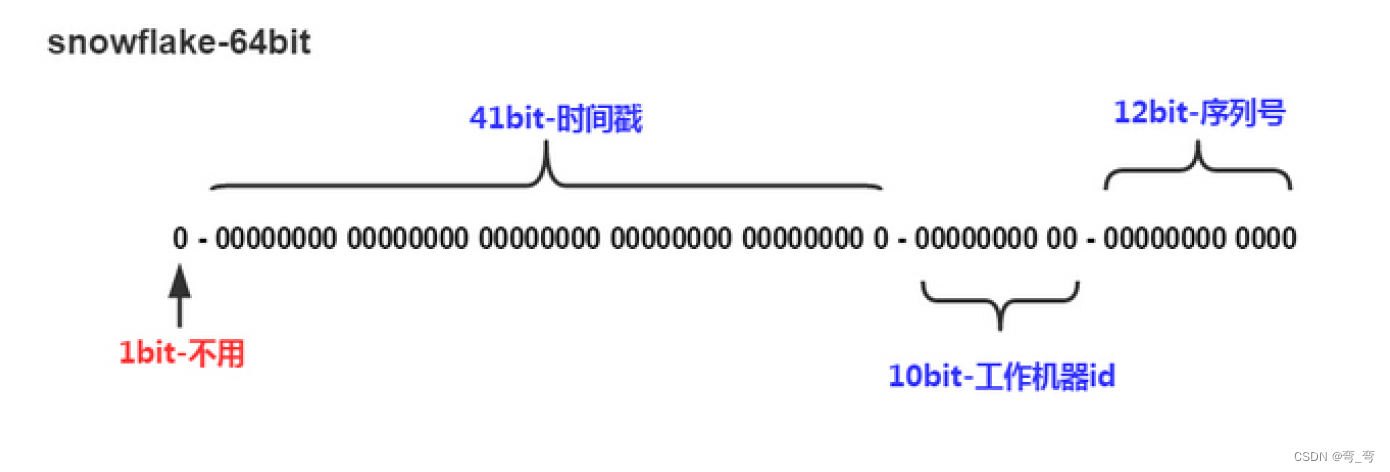
在高并发、高性能、高可用 三高项目中如何设计适合实际业务场景的分布式id(一)
分布式ID组件:黄金链路上的关键基石 在现代分布式系统中,分布式ID组件无疑扮演着至关重要的角色。作为整个系统的黄金链路上的关键组件,它的稳定性和可靠性直接关乎到整个系统的正常运作。一旦分布式ID组件出现问题,黄金链路上的…...
redis最新版本在Windows系统上的安装
一、说明 这次安装操作主要是根据redis官网说明,一步步安装下来的,英语比较好的同学,可以直接看文章底部的超链接1,跳到官网按步操作即可。 目前redis的最新稳定版本为redis7.2。 二、Windows环境改造 Redis在Windows上不被官方…...

【深度优先】【图论】【C++算法】2045. 到达目的地的第二短时间
作者推荐 视频算法专题 LeetCode2045. 到达目的地的第二短时间 城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] [ui, vi] 表…...

思维题(蓝桥杯 填空题 C++)
目录 题目一: 编辑 代码: 题目二: 代码: 题目三: 代码: 题目四: 代码: 题目五: 代码: 题目六: 代码七: 题目八&#x…...

Meta的Llama2模型已上线!但我为何更推荐你从HuggingFace获取?还有Code Llama等你来解锁!
嘿,朋友们,今天给你们介绍一个新东西——Llama2模型,这是Meta(对,就是Facebook那家)推出的。 你可以直接去Llama的官网下载这个模型,然后按照他们GitHub上的指南来调用。 不过呢,我…...
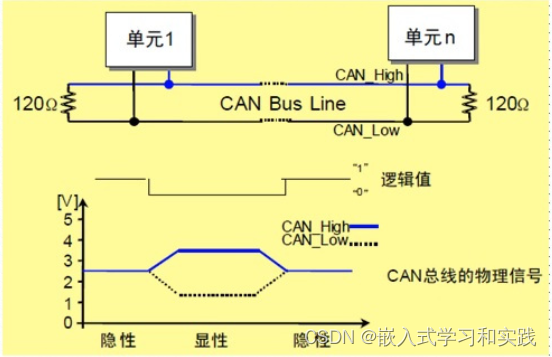
CAN总线及通讯的工作原理
一、CAN总线 CAN是控制器局域网络(Controller Area Network)的简称, 它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的, 并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。 二、工作原理 …...

linux下修改网卡MAC地址
我建议你使用 macchanger,但如果你不想使用它,那么可以使用另一种方法在 Linux 中更改 MAC 地址。 首先,使用以下命令关闭网卡: sudo ip link set dev enp0s31f6 down 接下来,使用以下命令设置新的 MAC:…...
47、WEB攻防——通用漏洞Java反序列化EXP生成数据提取组件安全
文章目录 序列化和反序列化的概念: 序列化:把java对象转换成字节流的过程;反序列化:把字节流恢复为java对象的过程。 对象的序列化主要有两种用途: 把对象的字节流永久的保存在硬盘上,通常存放在一个文件…...
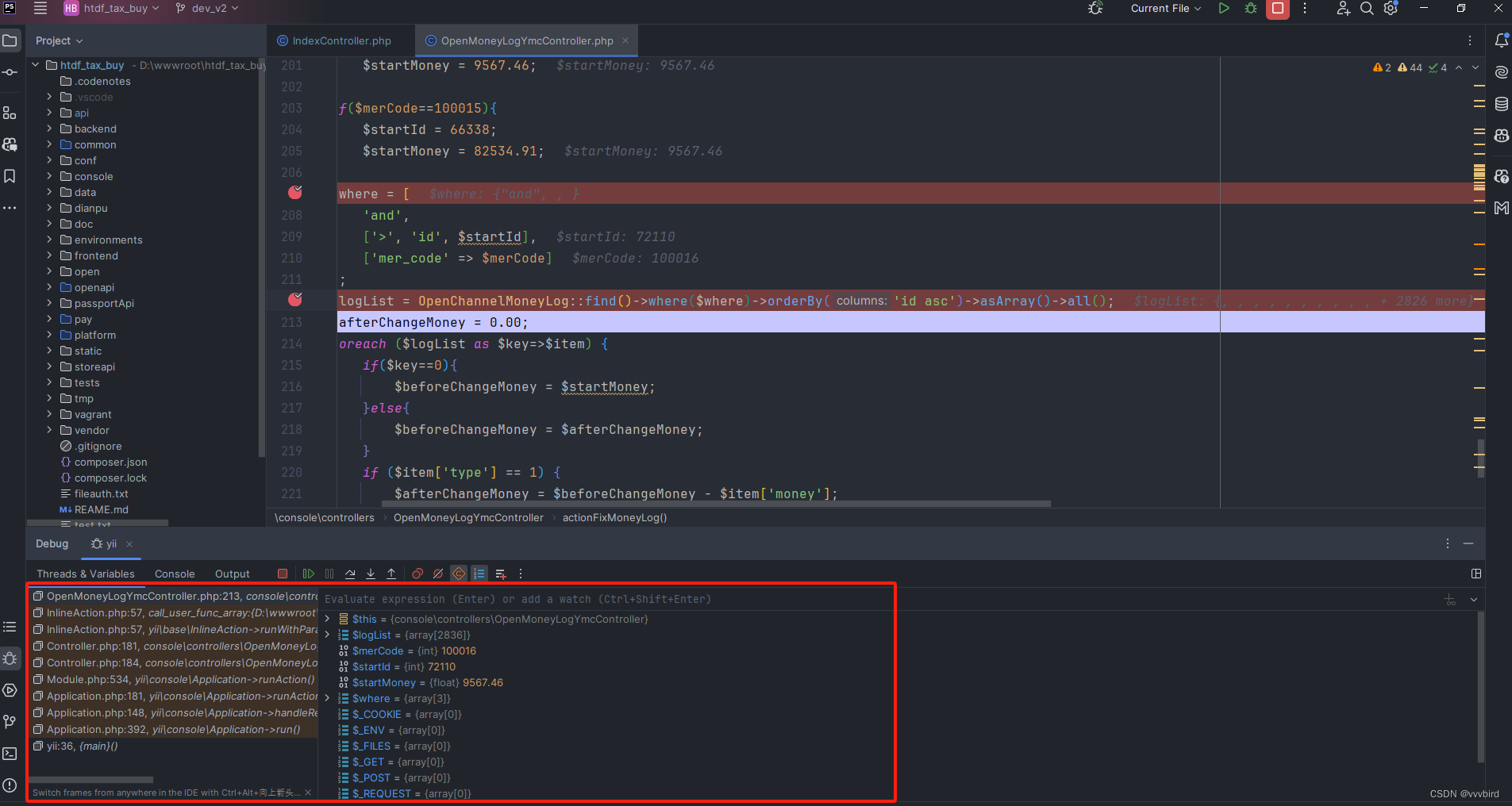
phpstorm console xdebug
1.所有配置跟浏览器http请求一样 2.记得Current File 必须是controller文件 注意:如果没有出发断点,则echo phpinfo(),查看remote_port 和phpstorm 配置是否对上。...

Vue template到render过程
Vue template到render过程 vue的模版编译过程主要如下:template -> ast -> render函数(1)调用parse方法将template转化为ast(抽象语法树)(2)对静态节点做优化(3)生…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
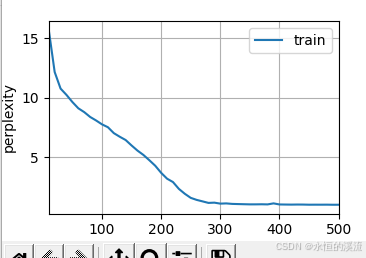
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...




