备战蓝桥杯---动态规划的一些思想2
话不多说,直接看题:
1.换根DP:
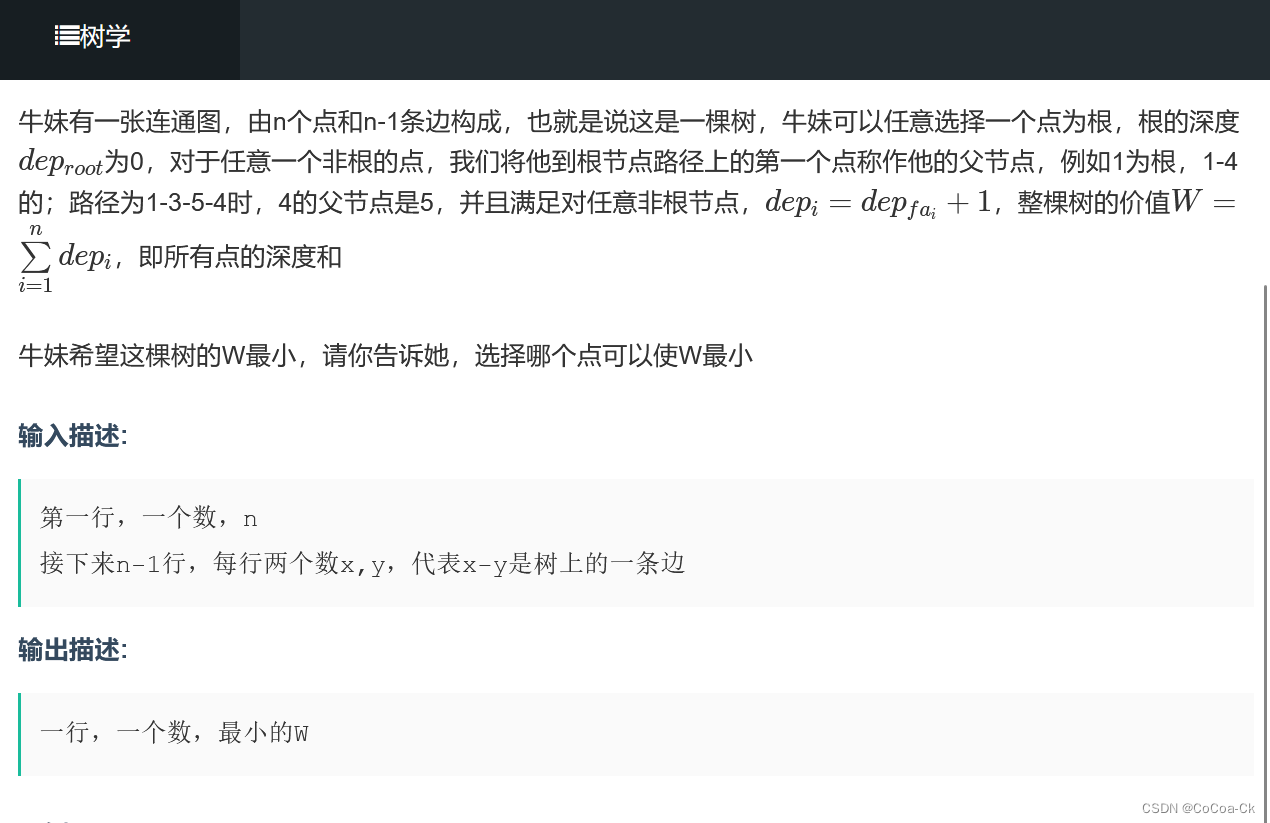
我们肯定不能对每一个根节点暴力求,我们不妨先求f[1],我们发现当他的儿子作为根节点时深度和为f[1]+(n-cnt[i])-cnt[i](cnt[i]表示以i为根的节点数),这样子两遍DFS即可,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,x,y,cnt[1000020],dep[1000010];
long long f[1000010];
vector<int> edge[1000010];
void dfs1(int root,int fa){cnt[root]=1;for(int i=0;i<edge[root].size();i++){int w=edge[root][i];if(w==fa) continue;dep[w]=dep[root]+1;dfs1(w,root);cnt[root]+=cnt[w];}return;
}
void dfs2(int root,int fa){for(int i=0;i<edge[root].size();i++){int w=edge[root][i];if(w==fa) continue;f[w]=f[root]+n-2*cnt[w];dfs2(w,root);}return;
}
int main(){cin>>n;for(int i=1;i<=n-1;i++){scanf("%d%d",&x,&y);edge[x].push_back(y);edge[y].push_back(x);}dep[1]=0;dfs1(1,0);for(int i=1;i<=n;i++){f[1]+=dep[i];}dfs2(1,0);long long ans=f[1];for(int i=2;i<=n;i++){ans=min(ans,f[i]);}cout<<ans;
}2.数学问题的背包转化:
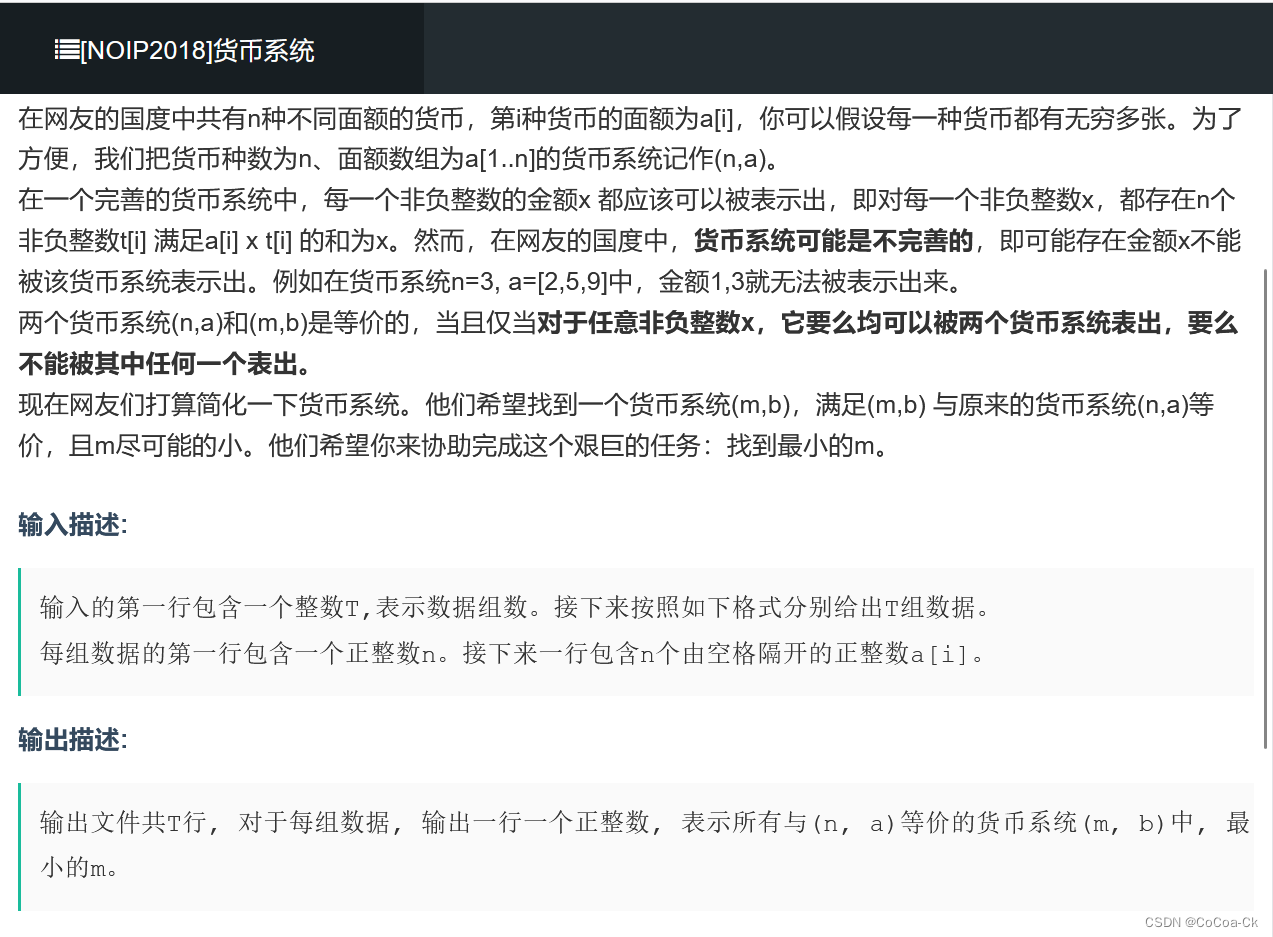
显然,我们要求的就是n个中的极大线性无关组,那么我们如何求?
只要一个数可以被比他小的组合表示出来,那么这个元素就可以删了。
如何实现?我们把每一个元素看成无穷个物品,我们判断一个元素是否可以被表示,就是看这个背包是否可以被塞满,因此变成了完全背包问题,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int a[110],n,t,m;
bool dp[25005];
bool cmp(int a,int b){return a<b;
}
int main(){cin>>t;while(t--){cin>>n;memset(dp,0,sizeof(dp));for(int i=1;i<=n;i++) scanf("%d",&a[i]);sort(a+1,a+n+1,cmp);m=n;dp[0]=1;for(int i=1;i<=n;i++){if(dp[a[i]]==1){m--;continue;}for(int j=a[i];j<=a[n];j++){dp[j]=dp[j-a[i]]||dp[j];}}cout<<m<<endl;}
}3.水题记录位置

就是在中序遍历上找根,再变成两个区间,用区间DP即可。
那么我们如何记录前序遍历呢,直接放在一维数组实现起来比较麻烦,于是我们可以用root[i][j]来记录i--j中选的根,然后再递归下去即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int dp[40][40],n,a[40],root[40][40];
int f(int l,int r){if(dp[l][r]>0) return dp[l][r];if(l==r) return dp[r][r]=a[r];if(l>r) return 1; int g=l;for(int i=l;i<=r;i++){if(dp[l][r]<=a[i]+f(l,i-1)*f(i+1,r)){dp[l][r]=a[i]+f(l,i-1)*f(i+1,r);g=i;}}root[l][r]=g;return dp[l][r];
}
void print(int l,int r){if(l==r){cout<<l<<" ";return;}if(l>r) return; cout<<root[l][r]<<" ";print(l,root[l][r]-1);print(root[l][r]+1,r);return;
}
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];cout<<f(1,n)<<endl;print(1,n);
}4.从小入手+两遍DP:

我们不妨先看一块,我们令f[k][i][x]表示第k条木板,前x个格子刷i次的最大正确粉刷格子数。
对于第k条木板,易得转移方程:f[k][i][x]=max(f[k][i-1][p]+w[p+1][x])(w[i][j]表示i--j一次刷最多可以刷对的格子数)
这样子,我们就把每一条木板刷的所有情况求出来,问题就转化成了分组背包。
我们令g[i][j]表示前i个木板刷了j次正确格子。
g[i][j]=g[i-1][k]+f[i][j-k][m].
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,t,a[60][60],f[55][2600][55],g[55][2600],ck0[55][55],ck1[55][55],ff[55][2600];
char x;
int main(){cin>>n>>m>>t;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf(" %c",&x);a[i][j]=x-'0';}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]==0){ck0[i][j]=ck0[i][j-1]+1;ck1[i][j]=ck1[i][j-1];}else{ck1[i][j]=ck1[i][j-1]+1;ck0[i][j]=ck0[i][j-1];}}}int x1,x2;for(int i=1;i<=n;i++){for(int j=1;j<=t;j++){for(int k=1;k<=m;k++){for(int p=0;p<=k;p++){x1=ck0[i][k]-ck0[i][p];x2=ck1[i][k]-ck1[i][p];f[i][j][k]=max(f[i][j][k],f[i][j-1][p]+max(x1,x2));}}}}for(int i=1;i<=n;i++){for(int j=1;j<=t;j++){for(int k=0;k<=j;k++){g[i][j]=max(g[i][j],f[i][k][m]+g[i-1][j-k]);}}}cout<<g[n][t];
}相关文章:

备战蓝桥杯---动态规划的一些思想2
话不多说,直接看题: 1.换根DP: 我们肯定不能对每一个根节点暴力求,我们不妨先求f[1],我们发现当他的儿子作为根节点时深度和为f[1](n-cnt[i])-cnt[i](cnt[i]表示以i为根的节点数),这样子两遍DFS…...
卫星导航 | 坐标系---地理坐标系与UTM坐标系
卫星导航 | 坐标系---地理坐标系与UTM坐标系 世界坐标系地理坐标系UTM坐标系 全球卫星导航系统(Global Navigation Satelite System,GNSS),简称卫星导航,是室外机器人定位的一个主要信息来源。 卫星导航能给机器人提供什么信息? 正常工作时&…...

JavaEE之volatile关键字
一.内存可见性问题 什么是内存可见性问题 计算机运行的程序/代码,往往需要访问数据。这些数据往往存在于内存中。 cup使用此变量时,就会把内存中的数据先读出来,加载到cpu寄存器中,再去参与运算。 但是,关键是cpu读…...

代码学习记录10
随想录日记part10 t i m e : time: time: 2024.03.03 主要内容:今天的主要内容是深入了解数据结构中栈和队列,并通过三个 l e e t c o d e leetcode leetcode 题目深化认识。 20. 有效的括号1047. 删除字符串中的所有…...
java——2024-03-03
String类的对象能被修改吗?如果不能需要用什么修改?StringBuilder和StringBuffer的区别?equals和区别谈谈对面向对象的理解重载和重写的区别说一下ArrayList,LinkedList底层实现以及区别什么是哈希冲突?hashMap和conCu…...
Ubuntu安装conda以后,给jupyter安装C++内核
前言 大家都知道,jupyter notebook 可以支持python环境,可以在不断点调试的情况下,打印出当前结果,如果代码错了也不影响前面的内容。于是我就想有没有C环境的,结果还真有。 参考文章: 【分享】Ubuntu安装…...
)
【谈判】核心思想(抓大放小)
谈判交换(抓大放小) 一、明确目的 事:must: 非要不可,才会签字 want: 有很好, give: 放掉 三者,会变化 二、明确对象 人:我跟谁谈? 时: 国际形势、国家的政策、他的心…...
)
洛谷P5908 猫猫和企鹅 做题反思(2024.3.7)
猫猫和企鹅 题目传送门 题目描述 王国里有 n n n 个居住区,它们之间有 n − 1 n-1 n−1 条道路相连,并且保证从每个居住区出发都可以到达任何一个居住区,并且每条道路的长度都为 1 1 1。 除 1 1 1 号居住区外,每个居住区住…...
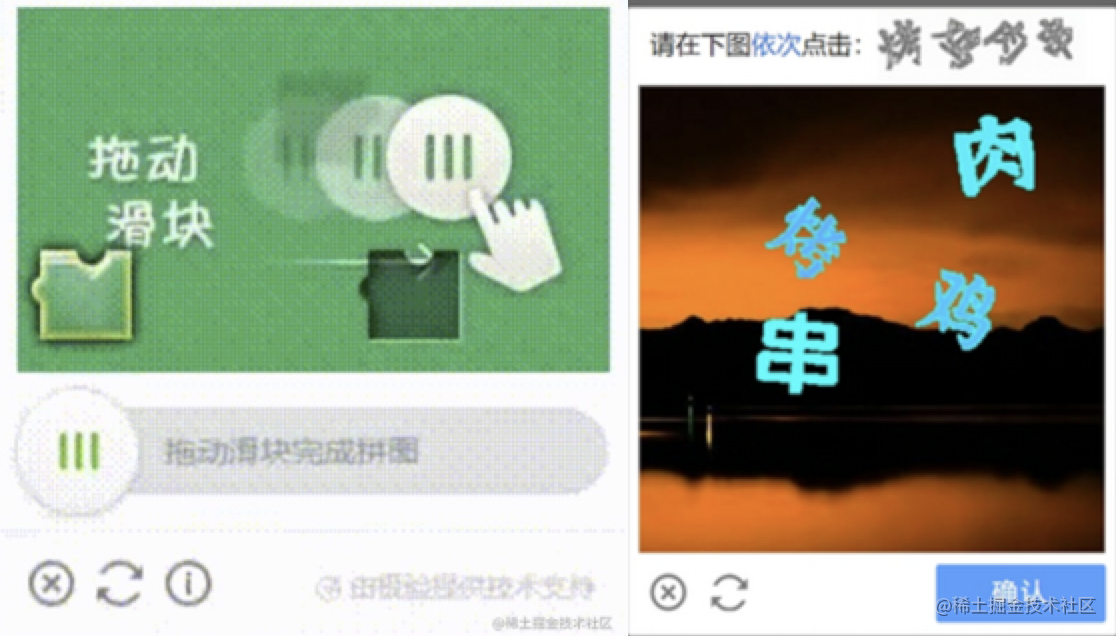
常见的验证码
一、短信验证码 前端: 用户填写手机号,点击按钮发送请求用户短信得到验证码后,用户填写表单提交 form 表单,进行验证 后台: 随机生成几位验证码并将生成时间、手机号、验证码存储起来,可以存到session、…...

11. C语言标准函数库
C语言制定了一组使用方式通用的函数,称为C语言标准函数库,用于实现编程常用功能,标准函数库由编译器系统提供,并按功能分类存储在不同源代码文件中,调用标准库内函数时需要首先使用 #include 连接对应的源代码文件。 【…...

2016年认证杯SPSSPRO杯数学建模C题(第一阶段)如何有效的抑制校园霸凌事件的发生解题全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 C题 如何有效的抑制校园霸凌事件的发生 原题再现: 近年来,我国发生的多起校园霸凌事件在媒体的报道下引发了许多国人的关注。霸凌事件对学生身体和精神上的影响是极为严重而长远的,因此对于这些情况我们应该…...

设计模式-抽象工厂模式实践案例
抽象工厂模式(Abstract Factory Pattern)是一种创建型设计模式,它提供了一个接口,用于创建一系列相关或相互依赖的对象,而无需指定它们具体的类。抽象工厂模式是围绕一个超级工厂创建其他工厂的模式。该模式的实现涉及…...

用readproc函数读取进程的状态
概要: 本篇演示用readproc函数读取进程的状态 libprocps库的安装参考笔者的文章readproc.h-CSDN博客 演示所用的系统是Ubuntu22.04 一、代码 #include<stdio.h> #include<stdlib.h> #include<proc/readproc.h> int main() {struct PROCTAB *…...
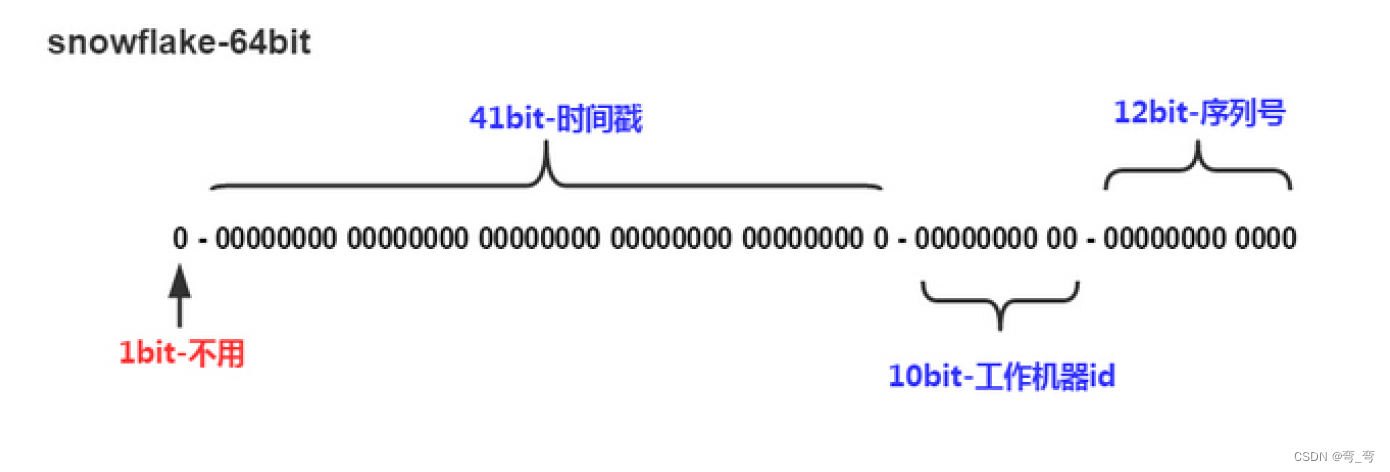
在高并发、高性能、高可用 三高项目中如何设计适合实际业务场景的分布式id(一)
分布式ID组件:黄金链路上的关键基石 在现代分布式系统中,分布式ID组件无疑扮演着至关重要的角色。作为整个系统的黄金链路上的关键组件,它的稳定性和可靠性直接关乎到整个系统的正常运作。一旦分布式ID组件出现问题,黄金链路上的…...
redis最新版本在Windows系统上的安装
一、说明 这次安装操作主要是根据redis官网说明,一步步安装下来的,英语比较好的同学,可以直接看文章底部的超链接1,跳到官网按步操作即可。 目前redis的最新稳定版本为redis7.2。 二、Windows环境改造 Redis在Windows上不被官方…...

【深度优先】【图论】【C++算法】2045. 到达目的地的第二短时间
作者推荐 视频算法专题 LeetCode2045. 到达目的地的第二短时间 城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] [ui, vi] 表…...

思维题(蓝桥杯 填空题 C++)
目录 题目一: 编辑 代码: 题目二: 代码: 题目三: 代码: 题目四: 代码: 题目五: 代码: 题目六: 代码七: 题目八&#x…...

Meta的Llama2模型已上线!但我为何更推荐你从HuggingFace获取?还有Code Llama等你来解锁!
嘿,朋友们,今天给你们介绍一个新东西——Llama2模型,这是Meta(对,就是Facebook那家)推出的。 你可以直接去Llama的官网下载这个模型,然后按照他们GitHub上的指南来调用。 不过呢,我…...
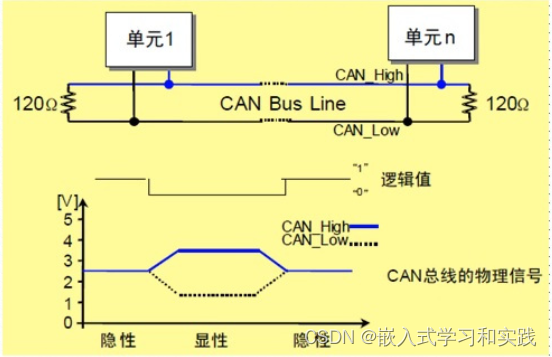
CAN总线及通讯的工作原理
一、CAN总线 CAN是控制器局域网络(Controller Area Network)的简称, 它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的, 并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。 二、工作原理 …...

linux下修改网卡MAC地址
我建议你使用 macchanger,但如果你不想使用它,那么可以使用另一种方法在 Linux 中更改 MAC 地址。 首先,使用以下命令关闭网卡: sudo ip link set dev enp0s31f6 down 接下来,使用以下命令设置新的 MAC:…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
