从根到叶:深入理解二叉搜索树
我们的心永远向前憧憬
尽管活在阴沉的现在
一切都是暂时的,转瞬即逝,
而那逝去的将变为可爱
🌝(俄) 普希金 <假如生活欺骗了你>

1.二叉搜索树的概念
概念:搜索树(Search Tree)是一种有序的数据结构,用于存储和组织一组元素。它提供高效的搜索、插入和删除操作。
组成:搜索树是由节点(Node)组成的树状结构,每个节点包含一个关键字(Key)和相关的数据(Data)。通过比较节点的关键字,可以确定元素在搜索树中的位置。
常见的搜索树包括二叉搜索树(Binary Search Tree)和平衡二叉搜索树(Balanced Binary Search Tree),如红黑树(Red-Black Tree)、AVL树等。
本篇文章主要讲的是二叉搜索树
在二叉搜索树中,每个节点最多有两个子节点,且左子节点的关键字小于父节点的关键字,右子节点的关键字大于父节点的关键字。这种有序性质使得在搜索树中进行搜索操作时,可以通过比较关键字的大小来决定搜索方向,从而快速地找到目标元素,简而言之如下:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
比如有一组数组:
int array[] = {{5,3,4,1,7,8,2,6,0,9}则它的二叉搜索树为:
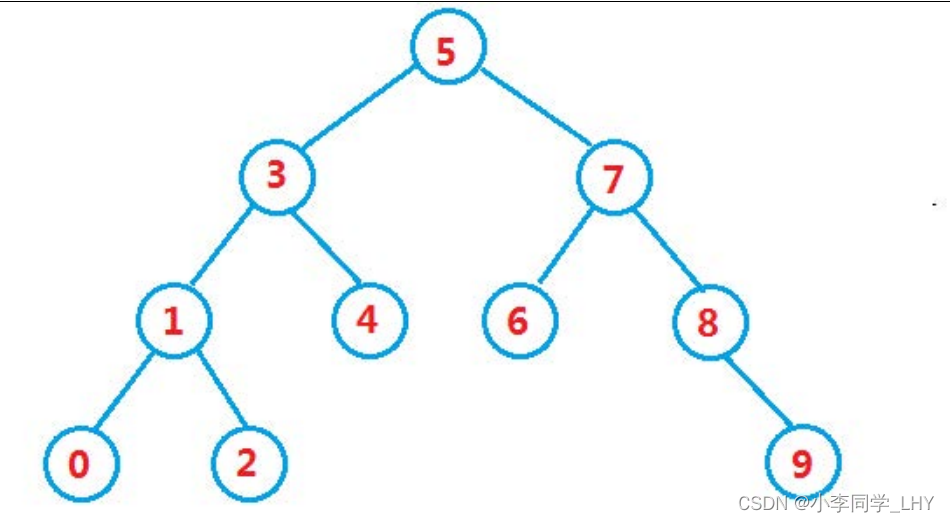
2.二叉搜索树的定义类
public class BinarySearchTree {static class TreeNode{public int val;//元素public TreeNode left;//左子树public TreeNode right;//右子树public TreeNode(int val){this.val = val;}}public TreeNode root;
}3.实现二叉搜索树的查找
执行步骤:
- 从root根节点开始,将要查找的关键字与当前节点的关键字进行比较。
- 如果要查找的key关键字等于当前节点的关键字,则找到了目标元素,查找成功。
- 如果要查找的key关键字小于当前节点的关键字,则继续在当前节点的左子树中进行查找。
- 如果要查找的key关键字大于当前节点的关键字,则继续在当前节点的右子树中进行查找。
- 如果当前节点的左子树或右子树为空,表示查找失败,目标元素不存在于树中。
- 重复步骤1-5,直到找到目标元素或确定目标元素不存在。
例子解释:
现在有一组数据:查找关键字8
int array[] = {{5,3,4,1,7,8,2,6,0,9}逻辑思路:
- 初始化一个指针,将其指向根节点,例如使用
cur指针,并将其初始值设置为根节点。 - 进入一个循环,循环条件是当前节点不为空,即
cur不为null。 - 在循环中,比较当前节点的关键字与目标关键字的大小关系。
- 如果当前节点的关键字小于目标关键字,说明目标元素应该在当前节点的右子树中,将当前节点指针
cur移动到右子节点,即cur = cur.right。 - 如果当前节点的关键字大于目标关键字,说明目标元素应该在当前节点的左子树中,将当前节点指针
cur移动到左子节点,即cur = cur.left。 - 如果当前节点的关键字等于目标关键字,表示已经找到了目标元素,可以返回
true或执行其他相应的操作。 - 如果循环结束仍然没有找到目标元素,即当前节点为空,表示查找失败,可以返回
false或执行其他相应的操作。
如视频展示:
二叉树搜索树-寻找
代码如下:
public boolean search(int key){TreeNode cur = root; // 初始化当前节点指针cur为根节点rootwhile(cur != null){ // 循环条件:当前节点cur不为空if(cur.val < key){ // 如果当前节点的值小于目标关键字keycur = cur.right; // 移动当前节点指针cur到右子节点}else if(cur.val > key){ // 如果当前节点的值大于目标关键字keycur = cur.left; // 移动当前节点指针cur到左子节点}else {return true; // 当前节点的值等于目标关键字key,找到了目标元素,返回true}}return false; // 循环结束仍然没有找到目标元素,返回false,表示查找失败
}时间复杂度:
- 平均情况下,二叉搜索树的查找操作时间复杂度为O(log n),其中n是二叉搜索树中的节点数。每次比较都可以将搜索范围缩小一半。
- 最坏情况下(只有左子树或右子树),如果二叉搜索树是非平衡树,查找操作的时间复杂度可能达到O(n),其中n是二叉搜索树中的节点数。树的结构类似于链表,需要遍历从根节点到叶子节点的路径。
空间复杂度:
- 在迭代方式的二叉搜索树查找中,只使用了常数级别的额外空间,即只有一个额外的指针用于保存当前节点的引用,因此空间复杂度为O(1)。
4.实现二叉搜索树的插入
执行步骤:
- 首先,检查根节点
root是否为空。如果为空,表示该二叉搜索树为空树,将新节点TreeNode(val)作为根节点插入,并返回true表示插入成功。 - 如果根节点不为空,初始化当前节点指针
cur为根节点root,父节点指针parent为null。 - 进入循环,条件为当前节点
cur不为空。 - 在循环中,比较当前节点
cur的值与待插入值val的大小关系: - 循环结束后,表明找到了合适的插入位置。创建新节点
TreeNode(val)。 - 判断父节点
parent的值与待插入值val的大小关系: - 返回
true,表示插入成功。
视频展示如下:
二叉树搜索树-插入
代码如下:
public boolean insert(int val){if(root == null){ // 如果根节点为空,将新节点作为根节点插入root = new TreeNode(val);return true;}TreeNode cur = root; // 初始化当前节点指针cur为根节点rootTreeNode parent = null; // 初始化父节点指针parent为空while(cur != null){ // 循环条件:当前节点cur不为空if(cur.val < val){ // 如果当前节点的值小于待插入值valparent = cur; // 更新父节点指针为当前节点cur = cur.right; // 移动当前节点指针cur到右子节点} else if (cur.val > val) { // 如果当前节点的值大于待插入值valparent = cur; // 更新父节点指针为当前节点cur = cur.left; // 移动当前节点指针cur到左子节点} else{ // 如果当前节点的值等于待插入值val,即已存在相同值的节点return false; // 返回false,表示插入失败(不允许插入重复值)}}TreeNode node = new TreeNode(val); // 创建新节点if(parent.val > val){ // 如果父节点的值大于待插入值valparent.left = node; // 将新节点插入为父节点的左子节点}else {parent.right = node; // 将新节点插入为父节点的右子节点}return true; // 返回true,表示插入成功
}时间复杂度:
在最坏情况下,即二叉搜索树是一个非平衡树的情况下,插入操作的时间复杂度为O(n),其中n是二叉搜索树中的节点数。这种情况下,树的结构类似于链表,每次插入都需要遍历从根节点到叶子节点的路径。
在平均情况下,二叉搜索树的插入操作的时间复杂度为O(log n),其中n是二叉搜索树中的节点数。每次插入操作都可以将搜索范围减半,因此插入操作的时间复杂度是对数级别的。
空间复杂度:
在二叉搜索树的插入操作中,只需要使用常数级别的额外空间,即只有几个指针变量用于保存当前节点和父节点的引用。因此,插入操作的空间复杂度为O(1)。
5.实现二叉搜索树的删除
具体删除操作分三种情况:
第一种情况:待删除节点cur没有左子节点。
- 如果
cur是根节点,直接将根节点指向其右子节点cur.right。 - 如果
cur是父节点parent的左子节点,将父节点的左子节点指向cur.right。 - 如果
cur是父节点parent的右子节点,将父节点的右子节点指向cur.right。
视频展示:
二叉搜索树-删除-1
第二种情况:待删除节点cur没有右子节点。
- 如果
cur是根节点,直接将根节点指向其左子节点cur.left。 - 如果
cur是父节点parent的左子节点,将父节点的左子节点指向cur.left。 - 如果
cur是父节点parent的右子节点,将父节点的右子节点指向cur.left。
视频展示
二叉树搜索树-删除-2
第三种情况:待删除节点cur既有左子节点又有右子节点。
注意:待删除结点的数据将来放的数据一定是比左边都大,比右边都小的数据
如何寻找数据?
要么在左树里面找到最大的数据[即左树最右边的数据]
要么在右树里面找到最小的数据[即右数最左边的数据]
下面我使用的是在右数找最小值
执行步骤:
- 找到待删除节点
cur的右子树中的最小节点target,即右子树中最左侧的节点。 - 将最小节点
target的值赋给待删除节点cur,相当于将cur节点的值替换为target节点的值。 - 删除最小节点
target,即对最小节点target执行第一种或第二种情况的删除操作。
视频展示:
二叉搜索树-删除-3

注意:
当target没有左孩子时,应当时targetParent.right == target.right
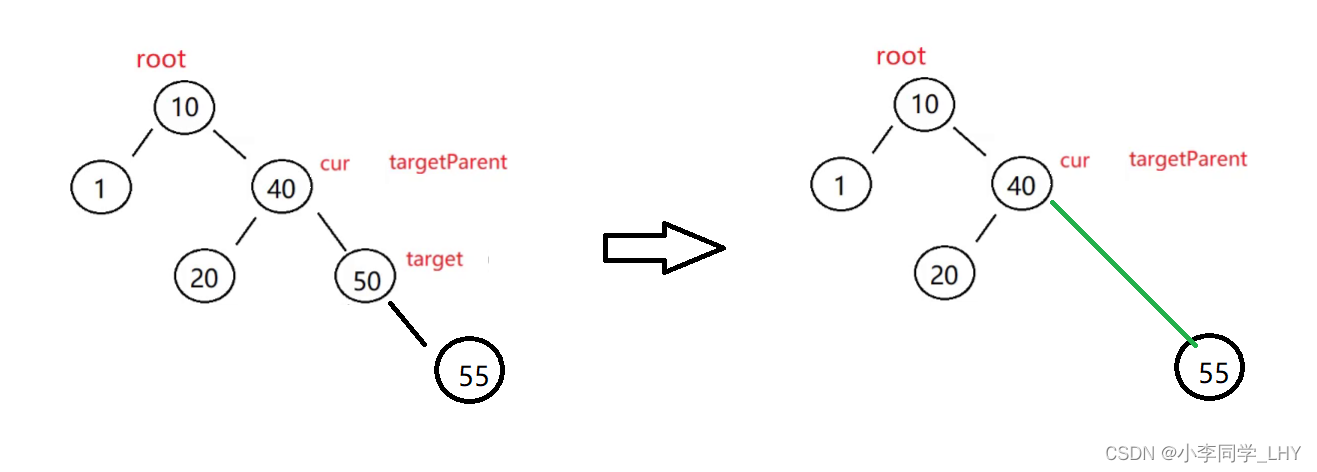
代码如下:
public void remove(int key){TreeNode cur = root; // 初始化当前节点指针cur为根节点rootTreeNode parent = null; // 初始化父节点指针parent为空while(cur != null){ // 循环条件:当前节点cur不为空if(cur.val < key){ // 如果当前节点的值cur.val小于待删除值keyparent = cur; // 更新父节点指针parent为当前节点curcur = cur.right; // 将当前节点指针cur移动到右子节点cur.right} else if (cur.val > key) { // 如果当前节点的值cur.val大于待删除值keyparent = cur; // 更新父节点指针parent为当前节点curcur = cur.left; // 将当前节点指针cur移动到左子节点cur.left} else { // 当前节点的值cur.val等于待删除值key,找到待删除节点removeNode(cur, parent); // 调用removeNode函数执行删除操作}}
}private void removeNode(TreeNode cur, TreeNode parent) {// 第一种情况:待删除节点cur没有左子节点if(cur.left == null){if(cur == root){ // 如果待删除节点cur是根节点root = cur.right; // 直接将根节点指向其右子节点cur.right} else if (cur == parent.left) { // 如果待删除节点cur是父节点parent的左子节点parent.left = cur.right; // 将父节点的左子节点指向cur.right} else { // 如果待删除节点cur是父节点parent的右子节点parent.right = cur.right; // 将父节点的右子节点指向cur.right}}// 第二种情况:待删除节点cur没有右子节点else if(cur.right == null){if(cur == root){ // 如果待删除节点cur是根节点root = cur.left; // 直接将根节点指向其左子节点cur.left} else if(cur == parent.left){ // 如果待删除节点cur是父节点parent的左子节点parent.left = cur.left; // 将父节点的左子节点指向cur.left} else { // 如果待删除节点cur是父节点parent的右子节点parent.right = cur.left; // 将父节点的右子节点指向cur.left}}// 第三种情况:待删除节点cur既有左子节点又有右子节点else {TreeNode targetParent = cur; // 初始化目标节点的父节点指针为curTreeNode target = cur.right; // 初始化目标节点指针为cur的右子节点while(target.left != null){ // 寻找cur右子树中的最小节点targetParent = target; // 更新目标节点的父节点指针为targettarget = target.left; // 将目标节点指针移动到左子节点target.left}cur.val = target.val; // 将目标节点的值赋给待删除节点cur,相当于替换值if(targetParent.left == target){ // 如果目标节点是其父节点的左子节点targetParent.left = target.right; // 将目标节点的右子节点连接到目标节点的父节点的左子节点上} else { // 如果目标节点是其父节点的右子节点targetParent.right = target.right; // 将目标节点的右子节点连接到目标节点的父节点的右子节点上}}
}时间复杂度:
- 在平均情况下,二叉搜索树的高度为O(log N),其中N是树中节点的总数。在删除节点的过程中,需要遍历树以找到待删除节点的位置,这需要沿着树的高度移动。因此,平均情况下删除节点的时间复杂度为O(log N)。
- 在最坏情况下,如果二叉搜索树是一个不平衡的树,即所有节点都只有一个子节点,删除节点的时间复杂度可以达到O(N),其中N是树中节点的总数。这种情况发生在树没有进行平衡操作或者插入和删除操作导致树失去平衡的情况下。
空间复杂度:
- 删除节点的过程中使用了常数级别的额外空间,主要是用于存储当前节点指针
cur和父节点指针parent。因此,删除节点的空间复杂度为O(1)。
6.总结
- 二叉搜索树的查找、插入和删除操作都是基于节点值的比较来进行的。
- 查找操作的时间复杂度为O(log N),其中N是树中节点的总数。插入和删除操作的时间复杂度也是O(log N),但在最坏情况下(树不平衡),时间复杂度可能达到O(N)。
- 二叉搜索树的插入和删除操作可以保持树的有序性,但如果插入和删除操作频繁且不平衡,可能会导致树的高度增加,降低操作效率。
- 为了解决不平衡问题,可以使用平衡二叉搜索树(如AVL树、红黑树)等数据结构来保持树的平衡性,以提高查找、插入和删除操作的性能。
结语:
二叉搜索树提供了一种简洁而强大的数据结构,它不仅仅是一棵树,更是一种思想。通过理解和应用二叉搜索树的原理,我们可以解决各种问题,如数据的排序、查找最小/最大值、范围查询等。
在结束之际,让我们怀着对二叉搜索树的敬意,继续探索和学习更多的数据结构和算法,为解决复杂的计算问题开辟新的道路。无论是在计算机科学的领域中,还是在生活的各个方面,二叉搜索树的智慧将继续指引我们前行。

相关文章:

从根到叶:深入理解二叉搜索树
我们的心永远向前憧憬 尽管活在阴沉的现在 一切都是暂时的,转瞬即逝, 而那逝去的将变为可爱 🌝(俄) 普希金 <假如生活欺骗了你> 1.二叉搜索树的概念 概念:搜索树(Search Tree)是一种有序的数据结构,用于存储和组…...

网络信息安全:11个常见漏洞类型汇总
一、SQL注入漏洞 SQL注入攻击(SQL Injection),简称注入攻击、SQL注入,被广泛用于非法获取网站控制权,是发生在应用程序的数据库层上的安全漏洞。 在设计程序,忽略了对输入字符串中夹带的SQL指令的检查&…...
阿里云服务器使用教程_2024建站教程_10分钟网站搭建流程
使用阿里云服务器快速搭建网站教程,先为云服务器安装宝塔面板,然后在宝塔面板上新建站点,阿里云服务器网aliyunfuwuqi.com以搭建WordPress网站博客为例,来详细说下从阿里云服务器CPU内存配置选择、Web环境、域名解析到网站上线全流…...

【排序算法】推排序算法解析:从原理到实现
目录 1. 引言 2. 推排序算法原理 3. 推排序的时间复杂度分析 4. 推排序的应用场景 5. 推排序的优缺点分析 5.1 优点: 5.2 缺点: 6. Java、JavaScript 和 Python 实现推排序算法 6.1 Java 实现: 6.2 JavaScript 实现: 6.…...

Python爬虫实战(基础篇)—13获取《人民网》【最新】【国内】【国际】写入Word(附完整代码)
文章目录 专栏导读背景测试代码分析请求网址请求参数代码测试数据分析利用lxml+xpath进一步分析将获取链接再获取文章内容测试代码写入word完整代码总结专栏导读 🔥🔥本文已收录于《Python基础篇爬虫》 🉑🉑本专栏专门针对于有爬虫基础准备的一套基础教学,轻松掌握Py…...

常见控件应用
常见控件应用 1.操作Ajax选项2.滑动滑块操作 1.操作Ajax选项 Ajax即Asynchronous JavaScript and XML(异步JavaScript和XML),是指一种创建交互式、快速动态网页应用的网页开发技术。通过在后台与服务器进行少量数据交换,Ajax可以…...
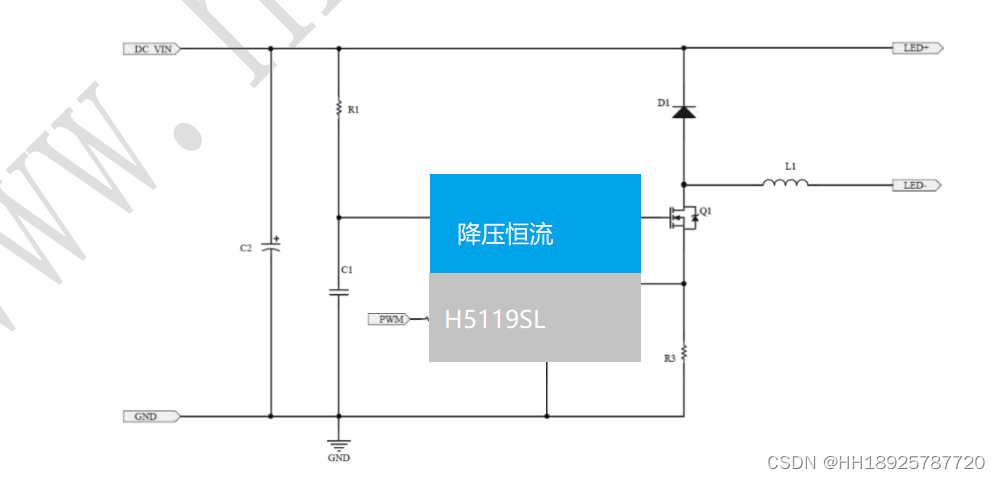
什么是降压恒流芯片?它有什么作用?
降压恒流芯片是一种电子元件,用于将高电压或高电流的输入电源转换为稳定的低电压输出电源,并同时保持恒定的电流输出。 降压恒流芯片的作用有以下几点: 将高电压降低到适合驱动车灯的工作电压,确保车灯亮度稳定。 在负载变化时…...
14:00面试,15:00就出来了,问的问题过于变态了。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到2月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%…...

Maven的settings.xml配置
maven的两大配置文件:settings.xml和pom.xml。其中settings.xml是maven的全局配置文件,pom.xml则是文件所在项目的局部配置 标签servers: 一般,仓库的下载和部署是在pom.xml文件中的repositories和distributionManagement元素中定…...
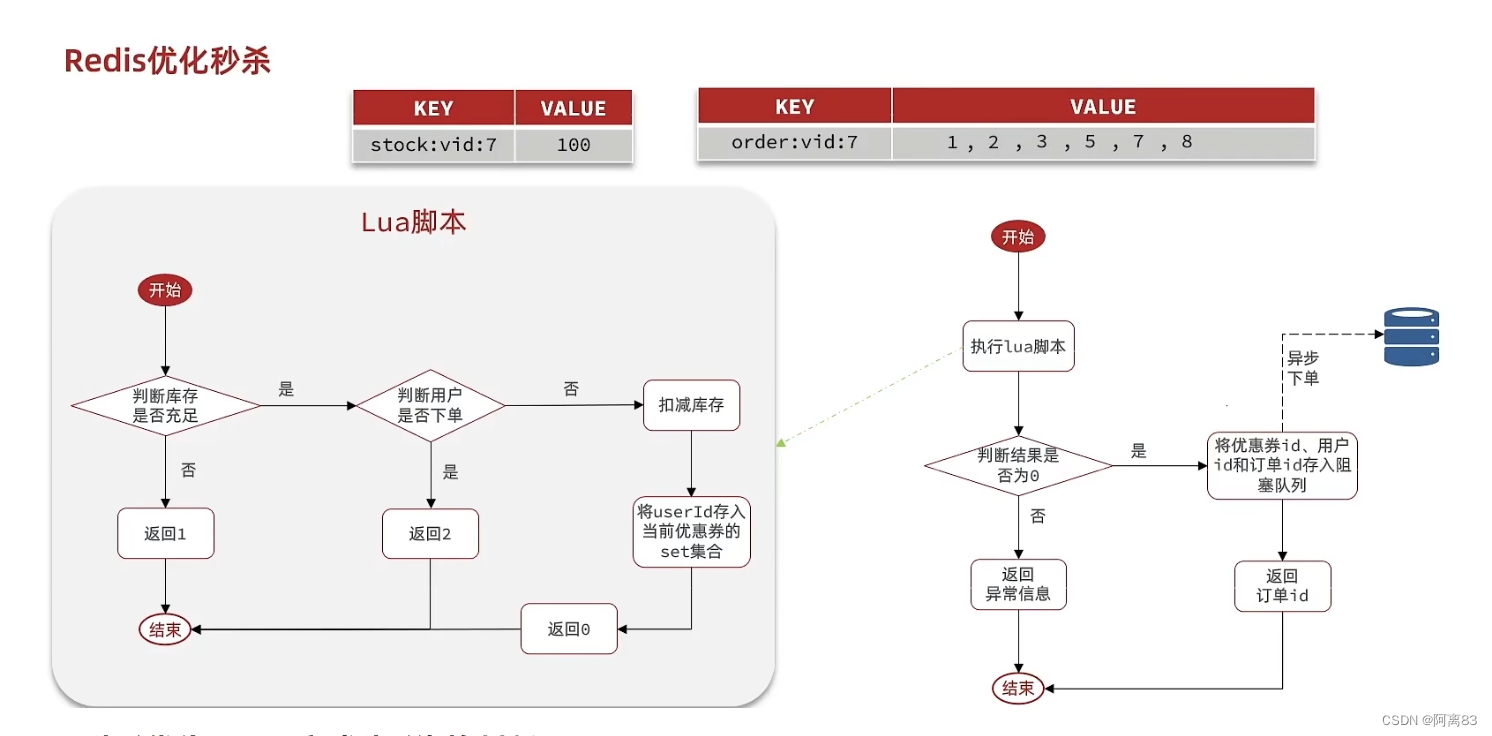
利用redis实现秒杀功能
6、秒杀优化 这个是 图灵 的redis实战里面的一个案例 6.1 秒杀优化-异步秒杀思路 我们来回顾一下下单流程 当用户发起请求,此时会请求nginx,nginx会访问到tomcat,而tomcat中的程序,会进行串行操作,分成如下几个步骤…...
vscode 使用ssh进行远程开发 (remote-ssh),首次连接及后续使用,详细介绍
在vscode添加remote ssh插件 首次连接 选择左侧栏的扩展,并搜索remote ssh 它大概长这样,点击安装 安装成功后,在左侧栏会出现远程连接的图标,点击后选择ssh旁加号便可以进行连接。 安装成功后vscode左下角会有一个图标 点击图…...

rabbitmq总结
一、初次感知 https://www.cnblogs.com/zqyx/p/13170881.html 这篇文章非常好,讲了一些持久化的原理。 1. 第一次使用rabbitmq发信息 // 创建连接工厂ConnectionFactory connectionFactorynew ConnectionFactory();connectionFactory.setHost("192.168.88.1…...

专利预审是什么
专利预审是一种专利申请流程中的前置审查服务,通常由国家知识产权局设立的各地方知识产权保护中心或其他指定机构提供。在正式提交专利申请至国家知识产权局之前,申请人可以通过专利预审机制,提前向预审机构提交专利申请资料,由预…...

淘宝商品详情数据丨商品搬家丨商品采集丨商城建站
淘宝商品详情数据、商品搬家、商品采集以及商城建站都是电子商务领域的重要环节,它们共同构成了一个完整的在线销售体系。下面我将分别对这几个概念进行详细的解释。 请求示例,API接口接入Anzexi58 一、淘宝商品详情数据 淘宝商品详情数据指的是在淘宝…...

redis(1)-key-value-基本概念
1. 全量IO 全局遍历 2.路由、索引、映射 3.文件里都是小格子,4KB 硬件水平的吞吐。 数据:索引 100:1 4.Mysql qps:90000 tps:5000 事务 1个事务 18 tps*18qps 1.安全 2.事务 3.持久化 4.淘汰 5.过期 定时:内存-mysql 一天…...

cocos creator 3.7.2使用shader实现图片扫光特效
简介 功能:图片实现扫光效果 引擎:cocos Creator 3.7.2 开发语言:ts 完整版链接 链接https://lengmo714.top/284d90f4.html 效果图 shader代码 // Copyright (c) 2017-2020 Xiamen Yaji Software Co., Ltd. CCEffect %{techniques:- pas…...

【C++杂货铺】详解string
目录 🌈前言🌈 📁 为什么学习string 📁 认识string(了解) 📁 string的常用接口 📂 构造函数 📂 string类对象的容量操作 📂 string类对象的访问以及遍历操…...
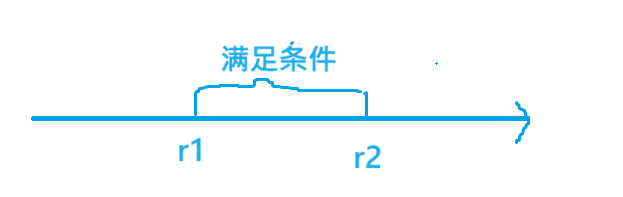
算法刷题day20:二分
目录 引言概念一、借教室二、分巧克力三、管道四、技能升级五、冶炼金属六、数的范围七、最佳牛围栏八、套餐设计九、牛的学术圈I十、我在哪? 引言 这几天一直在做二分的题,都是上了难度的题目,本来以为自己的二分水平已经非常熟悉了&#x…...

【Spring云原生】Spring Batch:海量数据高并发任务处理!数据处理纵享新丝滑!事务管理机制+并行处理+实例应用讲解
🎉🎉欢迎光临🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟特别推荐给大家我的最新专栏《Spring 狂野之旅:从入门到入魔》 🚀 本…...

docker ubuntu20.04 安装教程
ubuntu20.04 安装 docker 教程 本博客测试安装时间2023.8月 一、docker安装内容:docker Engine社区版 和 docker Compose 二、安装环境:ubuntu20.04 三、安装步骤: # 如果已经安装过docker,请先卸载,没安装则跳过…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
