2402. 2-SAT 问题(tarjan,2-SAT模板题)
活动 - AcWing
给定 n 个还未赋值的布尔变量 x1∼xn。
现在有 m 个条件,每个条件的形式为 “xi 为 0/1 或 xj 为 0/1 至少有一项成立”,例如 “x1 为 1 或 x3 为 0”、“x8 为 0 或 x4 为 0” 等。
现在,请你对这 n 个布尔变量进行赋值(0 或 1),使得所有 m 个条件能够成立。
输入格式
第一行包含两个整数 n,m。
接下来 m 行,每行包含四个整数 i,a,j,b,用来描述一个条件,表示 “xi 为 a 或 xj 为 b”。
输出格式
如果问题有解,则第一行输出 POSSIBLE,第二行输出 n 个整数表示赋值后的 n 个变量 x1∼xn 的值(0 或 1),整数之间用单个空格隔开。
如果问题无解,则输出一行 IMPOSSIBLE 即可。
如果答案不唯一,则输出任意一种正确答案即可。
数据范围
1≤n,m≤106,
1≤i,j≤n,
0≤a,b≤1
输入样例:
3 2
1 1 3 1
2 0 3 0
输出样例:
POSSIBLE
1 1 0解析:
该文件无法打开 - AcWing
本题是 2-SAT 问题的模板题,对于每个条件 a∧b,得出推导公式 −a→b 和 −b→a,按照推导公式建图,然后求强连通分量并进行缩点,如果任意一个变量的两种取值在同一个强连通分量中,说明无解。否则枚举每个变量,选取所在强连通分量拓扑序靠后的取值。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 2e6+10, M = 2e6+ 10, INF = 0x3f3f3f3f;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], ts;
int stk[N], top;
bool in_stk[N];
int id[N],cnt;void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int tarjan(int u) {dfn[u] = low[u] = ++ts;stk[++top] = u, in_stk[u] = 1;for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i];if (!dfn[j]) {tarjan(j);low[u] = min(low[u], low[j]);}else if (in_stk[j]) {low[u] = min(low[u], dfn[j]);}}if (dfn[u] == low[u]) {int y;cnt++;do {y = stk[top--];in_stk[y] = 0;id[y] = cnt;} while (y != u);}
}int main() {cin >> n >> m;memset(h, -1, sizeof h);for (int i = 1,x,a,y,b; i <= m; i++) {scanf("%d%d%d%d", &x, &a, &y, &b);x--, y -- ;add(2 * x + !a, 2 * y + b);add(2 * y + !b, 2 * x + a);}for (int i = 0; i < 2 * n; i++) {if (!dfn[i])tarjan(i);}for (int i = 0; i < n; i++) {if (id[i * 2] == id[2 * i + 1]) {cout << "IMPOSSIBLE" << endl;return 0;}}cout << "POSSIBLE" << endl;for (int i = 0; i < n; i++) {if (id[i * 2] < id[i * 2 + 1])printf("0 ");else printf("1 ");}return 0;
}相关文章:
)
2402. 2-SAT 问题(tarjan,2-SAT模板题)
活动 - AcWing 给定 n 个还未赋值的布尔变量 x1∼xn。 现在有 m 个条件,每个条件的形式为 “xi 为 0/1 或 xj 为 0/1 至少有一项成立”,例如 “x1 为 1 或 x3 为 0”、“x8 为 0 或 x4 为 0” 等。 现在,请你对这 n 个布尔变量进行赋值&am…...
基于java+springboot+vue实现的宠物健康咨询系统(文末源码+Lw)23-206
摘 要 本宠物健康咨询系统分为管理员还有用户两个权限,管理员可以管理用户的基本信息内容,可以管理公告信息以及宠物健康知识信息,能够与用户进行相互交流等操作,用户可以查看宠物健康知识信息,可以查看公告以及查看…...
品牌如何玩转饥饿营销?媒介盒子分享
饥饿营销是许多品牌都会用的策略,从“限定发售”、“先到先得”、“季节限定”、“专属VIP”等都属于饥饿营销的范畴,为什么饥饿营销屡试不爽,原因就在于人们面对同等的收益和损失时,损失会令他们更加难以接受。今天媒介盒子就来和…...

Vue3:ref和reactive实现响应式数据
一、情景说明 在Vue2中,我们已经知道数据的响应式,是什么含义 就是,在data块中,定义的变量,在页面中引用后 任何地方修改了该变量,页面中引用的变量会立即显示最新数值。 这块,我们学习了 插值…...

二维码门楼牌管理系统应用场景:商业与零售业发展的助推器
文章目录 前言一、二维码门楼牌管理系统的基本功能二、商业和零售业中的应用场景三、二维码门楼牌管理系统的优势分析四、结论 前言 在数字化时代的浪潮中,二维码门楼牌管理系统凭借其独特的优势,正在逐步成为商业和零售业发展的新宠。它不仅能够为商家…...
【Linux进阶之路】网络 —— “?“ (下)
文章目录 前言一、概念铺垫1.TCP2.全双工 二、网络版本计算器1. 原理简要2. 实现框架&&代码2.1 封装socket2.2 客户端与服务端2.3 封装与解包2.4 请求与响应2.5 对数据进行处理2.6 主程序逻辑 3.Json的简单使用 总结尾序 前言 在上文我们学习使用套接字的相关接口进行了…...

【AIGC】Stable Diffusion的建模思想、训练预测方式快速
在这篇博客中,将会用机器学习入门级描述,来介绍Stable Diffusion的关键原理。目前,网络上的使用教程非常多,本篇中不会介绍如何部署、使用或者微调SD模型。也会尽量精简语言,无公式推导,旨在理解思想。让有…...
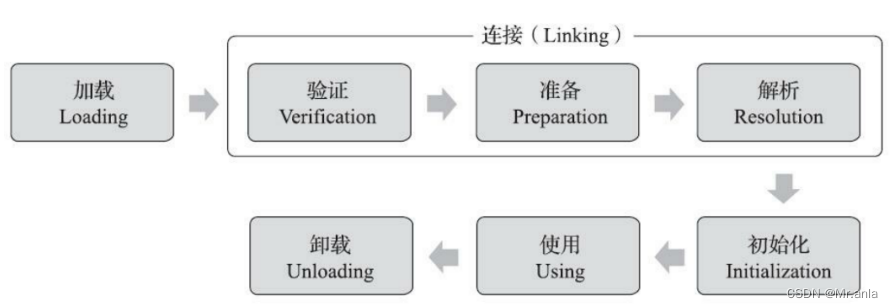
JVM(类加载机制)
类加载就是 .class 文件, 从文件(硬盘) 被加载到内存(元数据区)中的过程 类加载的过程 加载: 找 .class 文件的过程, 打开文件, 读文件, 把文件读到内存中 验证: 检查 .class 文件的格式是否正确 .class 是一个二进制文件, 其格式有严格的说明 准备: 给类对象分配内存空间 (先在…...

C++ 实战项目之 Boost 搜索引擎
项目地址:https://gitee.com/Vertas/boost-searcher-project 1. 项目背景 日常生活中我们使用过很多搜索引擎,比如百度,搜狗,360搜索等。我们今天是要实现一个像百度这样的搜索引擎嘛?那是不可能的,因为像…...

部署LVS+Keepalived高可用群集(抢占模式,非抢占模式,延迟模式)
目录 一、LVSKeepalived高可用群集 1、实验环境 2、 主和备keepalived的配置 2.1 yum安装ipvsadm和keepalived工具 2.2 添加ip_vs模块并开启ipvsadm 2.3 修改keepalived的配置文件 2.4 调整proc响应参数,关闭linux内核的重定向参数响应 2.5 将主服务器的kee…...

性别和年龄的视频实时监测项目
注意:本文引用自专业人工智能社区Venus AI 更多AI知识请参考原站 ([www.aideeplearning.cn]) 性别和年龄检测 Python 项目 首先介绍性别和年龄检测的高级Python项目中使用的专业术语 什么是计算机视觉? 计算机视觉是使计算机能…...

【Spring面试题】
目录 前言 1.Spring框架中的单例bean是线程安全的吗? 2.什么是AOP? 3.你们项目中有没有使用到AOP? 4.Spring中的事务是如何实现的? 5.Spring中事务失效的场景有哪些? 6.Spring的bean的生命周期。 7.Spring中的循环引用 8.构造方法…...

打车代驾小程序开发 醉酒不用怕一键找代驾
近年来,随着我国私家车市场的不断扩大,驾驶员的安全驾驶意识不断提高,以及交通法规对酒后驾驶的严格把握,代驾市场的潜力也在迸发。代驾小程序开发平台成为了代驾人不可或缺的线上接单平台。那么代驾小程序开发需要实现哪些功能呢…...

蓝桥集训之统计子矩阵
统计子矩阵 核心思想:矩阵前缀和 双指针 用i和j双指针 遍历所有子矩阵的列用s和t双指针 遍历所有子矩阵的行求其子矩阵的和 若>k 将s向下移动 矩阵和必定减小(元素个数减少)直到满足<k 因为列一定 行数即为方案数(从t行往上数到s行 共t-s1个区间[t,t][t-1,t]…...

架构师十项全能 你会几个?
架构设计导论 架构师核心能力 架构设计原则 架构设计模式 架构设计核心维度 架构图绘制 企业架构设计 分布式架构理论 微服务架构设计 响应式架构设计 架构设计评估 单元化架构设计 服务网络架构设计 DDD领域驱动设计 技术选型 服务治理设计 安全架构设计 云架构设计 数据库架构…...
数据库(mysql)-新手笔记(主外键,视图)
主外键 主键(唯一性,非空性) 主键是数据库表中的一个或多个字段,其值唯一标识表中的每一行/记录。 唯一性: 主键字段中的每个值都必须是唯一的,不能有两个或更多的记录具有相同的主键值 非空性:主键字段不能包含NULL值。 外键(引用完整 …...

西门子PLC的交互界面怎样设计?
西门子PLC的交互界面设计集中于提供一个直观、多功能且用户友好的环境,旨在使工程师和技术人员能够有效地进行编程、监控和维护。下面是一些设计西门子PLC交互界面时的关键考虑因素: 1. **图形化编程环境**:设计时,重点在于提供直…...
备份 ChatGPT 的聊天纪录
备份 ChatGPT 的聊天纪录 ChatGPT 在前阵子发生了不少次对话纪录消失的情况,让许多用户觉得困扰不已,也担心自己想留存的聊天记录消失不见。 好消息是,OpenAI 在 2023 年 4 月 11 日推出了 ChatGPT 聊天记录备份功能,无论是免费…...
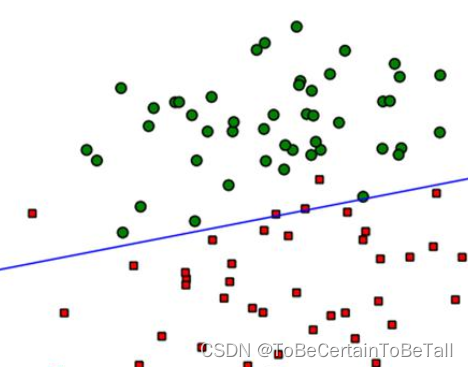
支持向量机 SVM | 线性可分:软间隔模型
目录 一. 软间隔模型1. 松弛因子的解释小节 2. SVM软间隔模型总结 线性可分SVM中,若想找到分类的超平面,数据必须是线性可分的;但在实际情况中,线性数据集存在少量的异常点,导致SVM无法对数据集线性划分 也就是说&…...

基于Java的生活废品回收系统(Vue.js+SpringBoot)
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容三、界面展示3.1 登录注册3.2 资源类型&资源品类模块3.3 回收机构模块3.4 资源求购/出售/交易单模块3.5 客服咨询模块 四、免责说明 一、摘要 1.1 项目介绍 生活废品回收系统是可持续发展的解决方案,旨在鼓…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
