Go语言数据结构(二)堆/优先队列
文章目录
- 1. container中定义的heap
- 2. heap的使用示例
- 3. 刷lc应用堆的示例
更多内容以及其他Go常用数据结构的实现在这里,感谢Star:https://github.com/acezsq/Data_Structure_Golang
1. container中定义的heap
在golang中的"container/heap"源码包中定义了堆的实现,我们在使用时需要实现heap接口中定义的方法,以此实现一个堆。
在container/heap.go中的heap接口的定义如下:
type Interface interface {sort.InterfacePush(x any) // add x as element Len()Pop() any // remove and return element Len() - 1.
}
而sort包中的接口定义如下:
type Interface interface {// Len is the number of elements in the collection.Len() int// Less reports whether the element with index i// must sort before the element with index j.//// If both Less(i, j) and Less(j, i) are false,// then the elements at index i and j are considered equal.// Sort may place equal elements in any order in the final result,// while Stable preserves the original input order of equal elements.//// Less must describe a transitive ordering:// - if both Less(i, j) and Less(j, k) are true, then Less(i, k) must be true as well.// - if both Less(i, j) and Less(j, k) are false, then Less(i, k) must be false as well.//// Note that floating-point comparison (the < operator on float32 or float64 values)// is not a transitive ordering when not-a-number (NaN) values are involved.// See Float64Slice.Less for a correct implementation for floating-point values.Less(i, j int) bool// Swap swaps the elements with indexes i and j.Swap(i, j int)
}
所以我们实现一个堆时需要实现这五个方法,然后相当于实现了这个接口,然后就可以调用container/heap.go中定义的Init方法、Push方法、Pop方法进行堆的基础入堆、出堆操作。
在使用这三个方法时,需要注意按照源码中定义的函数的入参和返回值的类型来使用。
// Init establishes the heap invariants required by the other routines in this package.
// Init is idempotent with respect to the heap invariants
// and may be called whenever the heap invariants may have been invalidated.
// The complexity is O(n) where n = h.Len().
func Init(h Interface) {// heapifyn := h.Len()for i := n/2 - 1; i >= 0; i-- {down(h, i, n)}
}
// Push pushes the element x onto the heap.
// The complexity is O(log n) where n = h.Len().
func Push(h Interface, x any) {h.Push(x)up(h, h.Len()-1)
}
// Pop removes and returns the minimum element (according to Less) from the heap.
// The complexity is O(log n) where n = h.Len().
// Pop is equivalent to Remove(h, 0).
func Pop(h Interface) any {n := h.Len() - 1h.Swap(0, n)down(h, 0, n)return h.Pop()
}
2. heap的使用示例
在golang的源码中也有堆的使用示例:
可以看到实现上我们用切片来作为heap的底层实现类型。
下面的代码是定义一个小根堆的示例,如果我们想定义一个存int类型数据的大根堆,只需要把Less函数中的小于号换成大于号即可。
// Copyright 2012 The Go Authors. All rights reserved.
// Use of this source code is governed by a BSD-style
// license that can be found in the LICENSE file.// This example demonstrates an integer heap built using the heap interface.
package heap_testimport ("container/heap""fmt"
)// An IntHeap is a min-heap of ints.
type IntHeap []intfunc (h IntHeap) Len() int { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }func (h *IntHeap) Push(x any) {// Push and Pop use pointer receivers because they modify the slice's length,// not just its contents.*h = append(*h, x.(int))
}func (h *IntHeap) Pop() any {old := *hn := len(old)x := old[n-1]*h = old[0 : n-1]return x
}// This example inserts several ints into an IntHeap, checks the minimum,
// and removes them in order of priority.
func Example_intHeap() {h := &IntHeap{2, 1, 5}heap.Init(h)heap.Push(h, 3)fmt.Printf("minimum: %d\n", (*h)[0])for h.Len() > 0 {fmt.Printf("%d ", heap.Pop(h))}// Output:// minimum: 1// 1 2 3 5
}3. 刷lc应用堆的示例
我们看一下23. 合并 K 个升序链表
这个题需要定义一个小根堆来存链表节点指针。
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func mergeKLists(lists []*ListNode) *ListNode {h := minHeap{}for _, head := range lists {if head != nil {h = append(h, head) }} heap.Init(&h) dummyhead := &ListNode{}cur := dummyheadfor len(h)>0 {node := heap.Pop(&h).(*ListNode)if node.Next != nil {heap.Push(&h, node.Next)}cur.Next = nodecur = cur.Next}return dummyhead.Next
}type minHeap []*ListNode
func (h minHeap) Len() int {return len(h)}
func (h minHeap) Less(i,j int) bool {return h[i].Val<h[j].Val}
func (h minHeap) Swap(i,j int) { h[i], h[j] = h[j], h[i]}
func (h *minHeap) Push(x any) { *h = append(*h, x.(*ListNode))}
func (h *minHeap) Pop() any { old:=*h; n:=len(old); x:=old[n-1]; *h=old[:n-1]; return x}
相关文章:

Go语言数据结构(二)堆/优先队列
文章目录 1. container中定义的heap2. heap的使用示例3. 刷lc应用堆的示例 更多内容以及其他Go常用数据结构的实现在这里,感谢Star:https://github.com/acezsq/Data_Structure_Golang 1. container中定义的heap 在golang中的"container/heap"…...
)
NERF论文笔记(1/2)
NeRF:Representing Scene as Neural Radiance Fields for View Synthesis 笔记 摘要 实现了一个任意视角视图生成算法:输入稀疏的场景图像,通过优化连续的Volumetric场景函数实现;用全连接深度网络表达场景,输入是一个连续的5维…...

深入理解nginx一致性哈希负载均衡模块[上]
1. 引言 在现代的网络应用中,负载均衡是一个至关重要的组件。它能够分配流量到多个服务器上,实现高可用性和性能扩展。Nginx是一个广泛使用的高性能Web服务器和反向代理服务器,其负载均衡模块提供了多种算法来实现流量的分发。其中࿰…...

【Linux】Docker安装
卸载旧版Docker 新版docker无法覆盖旧版的,所以需要先卸载原来的旧版本 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-selinux \docker-engine-selinux \docker-eng…...

动态SLAM论文阅读笔记
近期阅读了许多动态SLAM相关的论文,它们基本都是基于ORB-SLAM算法,下面简单记录一下它们的主要特点: 1.DynaSLAM 采用CNN网络进行分割多视图几何辅助的方式来判断动态点,并进行了背景修复工作。 2.Detect-SLAM 实时性问题&…...

数据挖掘:航空公司的客户价值分析
需求分析 理解并掌握聚类分析方法,掌握数据的标准化,掌握寻找最佳聚类数,掌握聚类的绘图,掌握聚类分析的应用场景。 系统实现 实验流程分析 借助航空公司数据,对客户进行分类对不同类别的客户进行特征分析…...

GIS之深度学习08:安装GPU环境下的pytorch
环境: cuda:12.1.1 cudnn:12.x pytorch:2.2.0 torchvision:0.17.0 Python:3.8 操作系统:win (本文安装一半才发现pytorch与cuda未对应,重新安装了cuda后才开始的&a…...

防患未然,OceanBase巡检工具应用实践——《OceanBase诊断系列》之五
1. OceanBase为什么要做巡检功能 尽管OceanBase拥有很好的MySQL兼容性,但在长期的生产环境中,部署不符合标准规范、硬件支持异常,或配置项错误等问题,这些短期不会出现的问题,仍会对数据库集群构成潜在的巨大风险。为…...
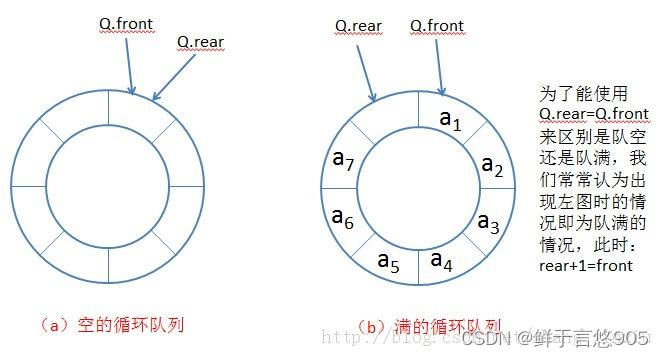
数据结构从入门到精通——队列
队列 前言一、队列1.1队列的概念及结构1.2队列的实现1.3队列的实现1.4扩展 二、队列面试题三、队列的具体实现代码Queue.hQueue.ctest.c队列的初始化队列的销毁入队列出队列返回队头元素返回队尾元素检测队列是否为空检测元素个数 前言 队列是一种特殊的线性数据结构ÿ…...
深度学习相关概念及术语总结
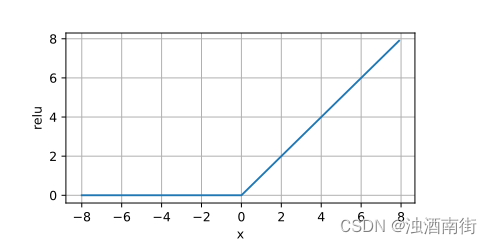
目录 1.CNN2.RNN3.LSTM4.NLP5.CV6.正向传播7.反向传播8.sigmoid 函数9.ReLU函数10.假设函数11.损失函数12.代价函数 1.CNN CNN 是卷积神经网络(Convolutional Neural Network)的缩写。卷积神经网络是一种深度学习模型,专门用于处理具有网格状…...
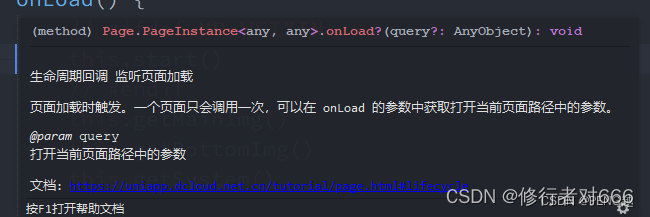
uniapp发行H5获取当前页面query
阅读uni的文档大致可得通过 onLoad与 onShow()的形参都能获取页面传递的参数,例如在开发时鼠标移动到方法上可以看到此方法的简短介绍 实际这里说的是打开当前页面的参数,在小程序端的时候测试并无问题,但是发行到H5时首页加载会造成参数获取…...

Flutter中动画的实现
动画三要素 控制动画的三要素:Animation、Tween、和AnmaitionController Animation: 产生的值的序列,有CurveAnimation等子类,, 可以将值赋值给Widget的宽高或其他属性,进而控制widget发生变化 Tween&#…...
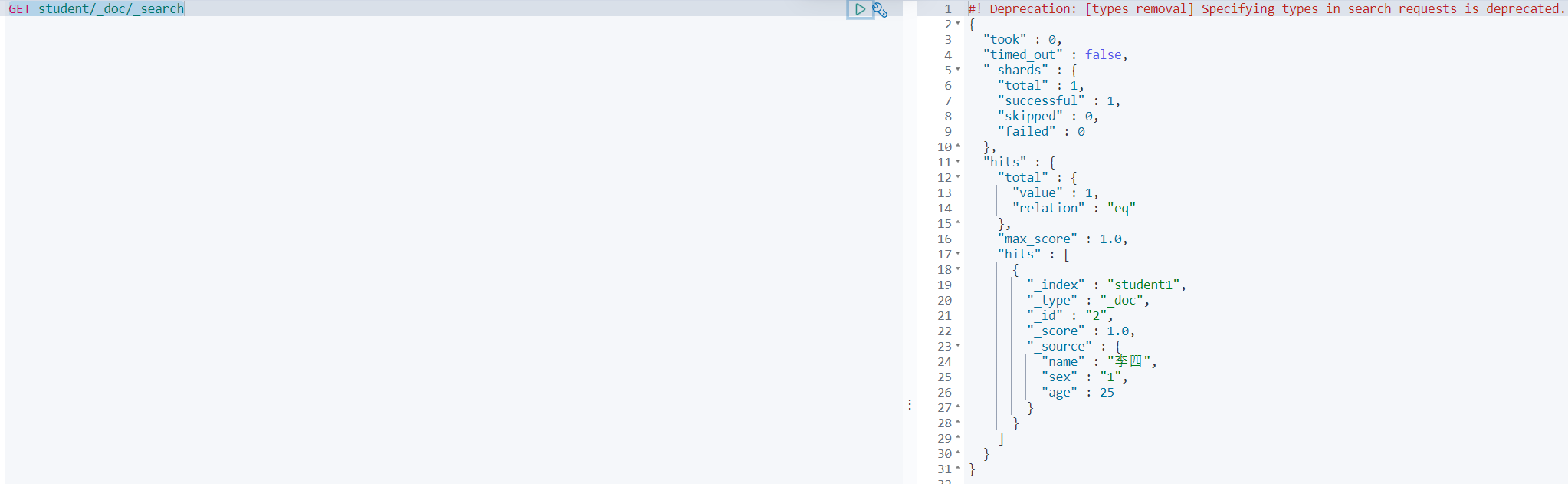
Elasticsearch从入门到精通-03基本语法学习
Elasticsearch从入门到精通-03基本语法学习 👏作者简介:大家好,我是程序员行走的鱼 📖 本篇主要介绍和大家一块学习一下ES基本语法,主要包括索引管理、文档管理、映射管理等内容 1.1 了解Restful ES对数据进行增、删、改、查是以…...
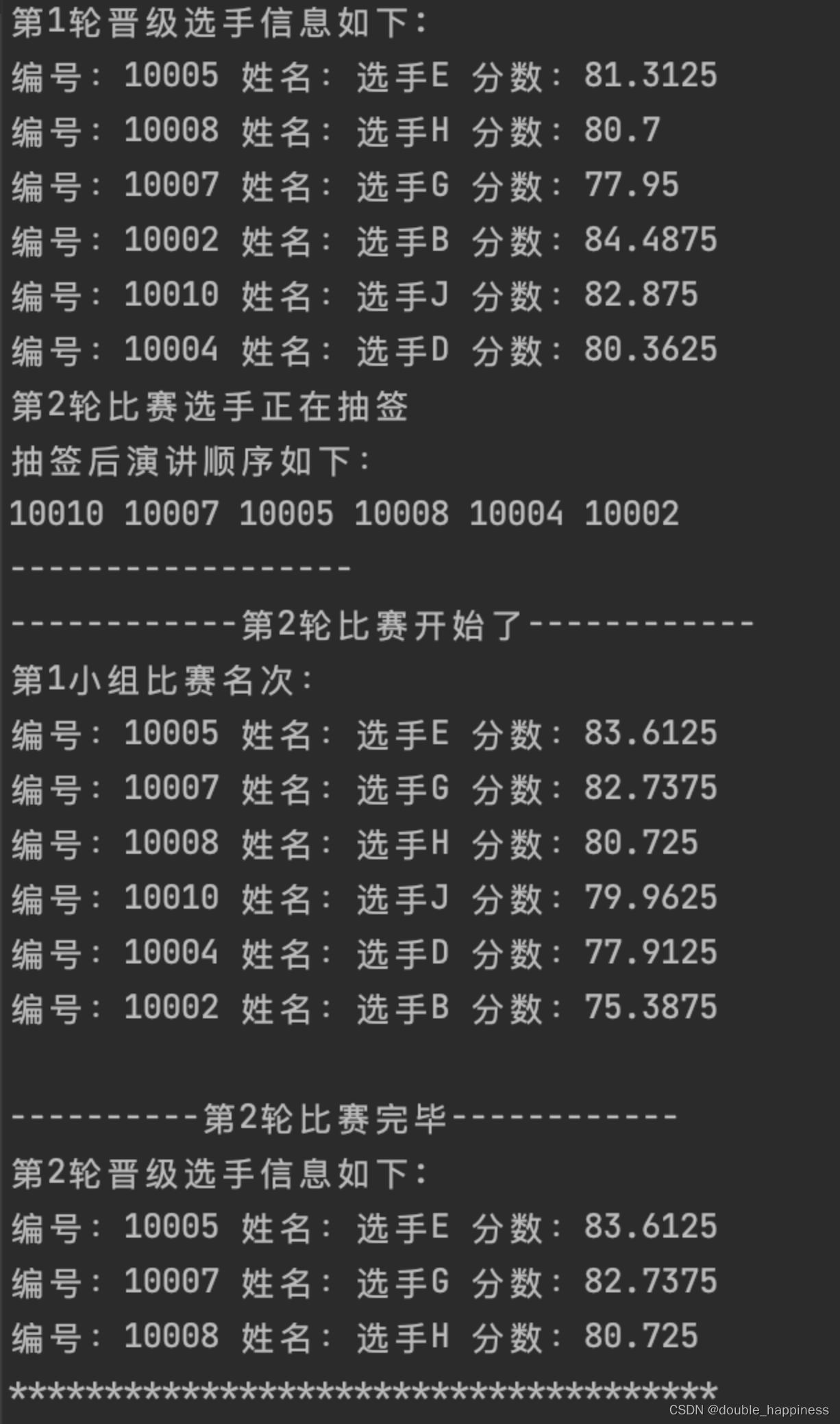
【黑马程序员】STL实战--演讲比赛管理系统
文章目录 演讲比赛管理系统需求说明比赛规则程序功能 创建管理类功能描述创建演讲比赛管理类 菜单功能添加菜单成员函数声明菜单成员函数实现菜单功能测试 退出功能添加退出功能声明退出成员函数实现退出功能测试 演讲比赛功能功能分析创建选手类比赛成员属性添加初始化属性创建…...
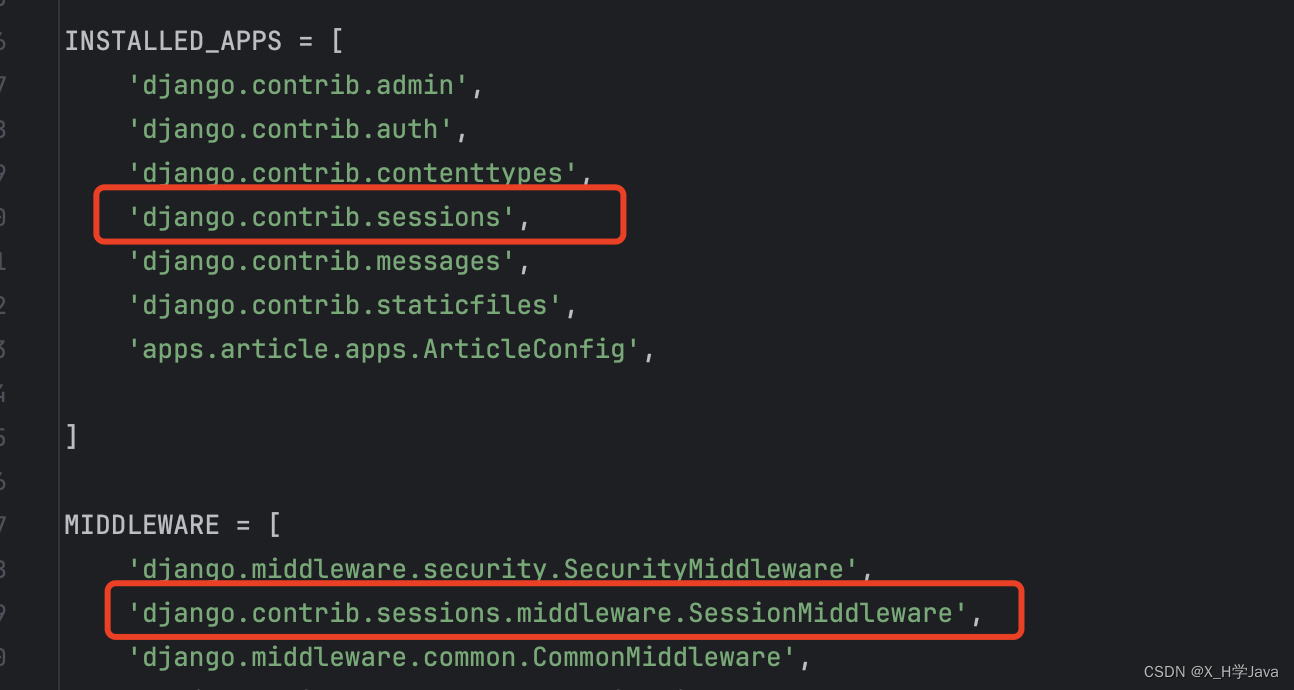
一文帮助快速入门Django
文章目录 创建django项目应用app配置pycharm虚拟环境打包依赖 路由传统路由include路由分发namenamespace 视图中间件orm关系对象映射操作表数据库配置model常见字段及参数orm基本操作 cookie和sessiondemo类视图 创建django项目 指定版本安装django:pip install dj…...
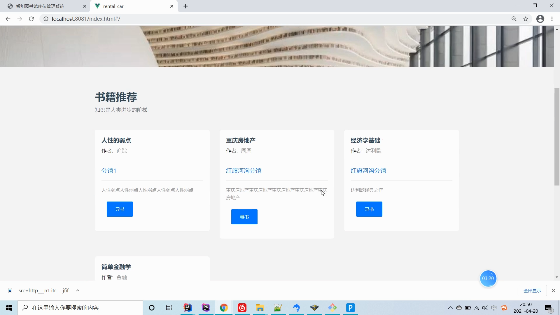
基于springboot实现图书推荐系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现图书馆推荐系统演示 摘要 时代的变化速度实在超出人类的所料,21世纪,计算机已经发展到各行各业,各个地区,它的载体媒介-计算机,大众称之为的电脑,是一种特高速的科学仪器,比…...

微信小程序实现上拉加载更多
一、前情提要 微信小程序中实现上拉加载更多,其实就是pc端项目的分页。使用的是scroll-view,scroll-view详情在微信开发文档/开发/组件/视图容器中。每次上拉,就是在原有数据基础上,拼接/合并上本次上拉请求得到的数据。这里采用…...
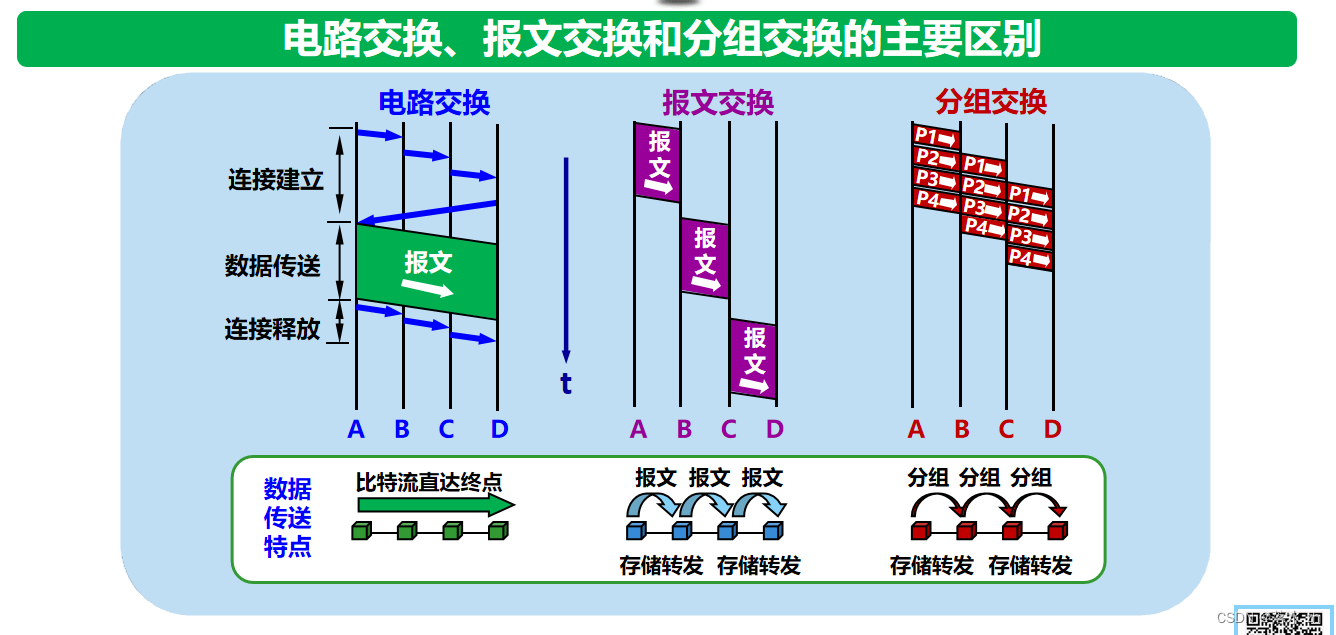
计算机网络——概述
计算机网络——概述 计算机网络的定义互连网(internet)互联网(Internet)互联网基础结构发展的三个阶段第一个阶段——APPANET第二阶段——商业化和三级架构第三阶段——全球范围多层次的ISP结构 ISP的作用终端互联网的组成边缘部分…...

kafka Interceptors and Listeners
Interceptors ProducerInterceptor https://www.cnblogs.com/huxi2b/p/7072447.html Producer拦截器(interceptor)是个相当新的功能,它和consumer端interceptor是在Kafka 0.10版本被引入的,主要用于实现clients端的定制化控制逻辑。 对于producer而言&…...

【面试题】mysql常见面试题及答案总结
事务中的ACID原则是什么? Mysql是如何实现或者保障ACID的? ACID原则是数据库事务管理中必须满足的四个基本属性,确保了数据库事务的可靠性和数据完整性。 简写全称解释实现A原子性(Atomicity)一个事务被视为一个不可分割的操作序列&#…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
