2024.03.04——2024.03.10 力扣练习总结及专项巩固(二)
1. (22. 括号生成)这里只讨论第二种做法回溯法。在回溯法的函数void backtrack(vector<string>& ans, string& current, int open, int close, int n); 中,可分为三个if条件判断,分别判断当current.size() == 2*n,open < n以及 ________ 的情况。首先当current.size() == 2*n时,可直接将当前字符串current入到ans当中;接着当open < n时,将'('入到当前字符串current当中,然后继续再调用回溯函数bactrack(ans, current, ____, close, n),值得注意的是,当调用完毕之后,还应该让当前字符串current pop出来一个字符。如果backtrack函数的原型变成void backtrack(vector<string>& ans, string current, int open, int close, int n); 其它的地方做一些适当的修改之后,那么在调用完毕之后还需要再让当前字符串current pop出来一个字符嘛?__________;最后当close < n时,将')'入到当前字符串current当中,然后继续再调用回溯函数backtrack(ans, current, open, _____, n)。同样在调用完毕之后,也还应该让当前字符串current再pop出来一个字符。我们会发现,回溯法的结构很类似于____________,即类似于下面的三部分代码:
void Traverse(TreeNode* pnode) {printf("%d", pnode->val);if(pnode->lchild) Traverse(pnode->lchild);_________________________________________;
}void Traverse(TreeNode* pnode) {if(pnode->lchild) Traverse(pnode->lchild);_______________________;if(pnode->rchild) Traverse(pnode->rchild);
}void Traverse(TreeNode* pnode) {_________________________________________;if(pnode->rchild) Traverse(pnode->rchild);printf("%d", pnode->val);
}2. (23. 合并K个有序链表)为了完成合并K个有序链表的任务,可以将这个任务拆分成两部分。首先编写合并两个有序链表的函数,接着再去编写合并K个有序链表的任务。在这里合并两个有序链表的方法可分为两种:递归法与哨兵结点法。递归法的函数为:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {if(l1 == nullptr && l2 != nullptr) {return l2;}else if(_____________________) {return l1;}else if(l1->val < l2->val) {l1->next = mergeTwoLists(____, ____);return __;}else{l2->next = mergeTwoLists(l1, ______);return l2;}
}哨兵结点法的函数为:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {ListNode* preHead = new ListNode(-1);ListNode* prev = preHead;while(l1 != nullptr && l2 != nullptr) {if(l1->val < l2->val){prev->next = l1;______________;}else{prev->next = l2;______________;}___________________;}if(l1 == nullptr){prev->next = l2;}else{prev->next = l1;}ListNode* ans = preHead->next;delete preHead; return ans;
}编写完合并两个有序链表的函数之后,开始编写合并K个有序链表的函数,在这里讨论三种方法。第一种方法就是顺序合并,即使用一个循环,依次将ans(ListNode*类型)与下一条链表进行合并;第二种方法是分治合并,即两两链表合并,合并完成之后再两两链表合并... ...顺序合并的代码是:
ListNode* mergeKLists(vector<ListNode*>& lists) {ListNode* ans = ________;for(int i = 0; i < lists.size(); i++) {ans = mergeTwoLists(lists[i], ___);}return ans;
}在顺序合并的代码中,必须让ans的初值为nullptr,而让i从0开始循环,这样做的原因是,如果ans初值为lists[0],i初值为0,则首轮循环时合并的两个链表是lists[0]与lists[0],这会导致程序卡死在合并两个有序链表上,具体表现是_________________。而如果ans初值为lists[0],i初值为1,则有可能出现K=0,即合并K个有序链表实质上就只是合并一个有序链表,这样子就会将不合适的lists[1]传给mergeTwoLists函数,进而导致错误。分治合并的代码是:
ListNode* mergeKLists(vector<ListNode*>& lists) {return merge(lists, 0, lists.size()-1);
}
ListNode* merge(vector<ListNode*>& lists, int l, int r) {if(l == r) return _______;else if(l > r) return ________;else{int min = (l+r)>>1;ListNode* lnode = merge(lists, l, mid);ListNode* rnode = ____________________;return mergeTwoLists(lnode, rnode);}
}3. (17. 电话号码的字母组合)这道题使用的是回溯算法。首先创建一个<char, string>类型的unordered_map类型的变量pairs,分别存储9个数字按键与26个英文字母之间的对应关系。接着编写主要的函数vector<string> letterCombinations(string digits)。在这个主要的函数中,先vector<string> ans;来保存结果,以及string combination来保存一次的字符串,接着如果digits的大小为0的话,直接返回空的ans,否则当调用backtrack函数之后,就会让一个空字符串进入到ans中,而这与我们的目标是不相符的。而如果digits的大小不为0,则调用backtrack函数,调用完backtrack函数之后,再return ans。因此主要的函数letterCombinations的结构为:
vector<string> letterCombinations(string digits) {vector<string> ans;__________________;if(digits.size() == 0) {__________;}else{backtrack(vector<string>& ans, string& combination, string& digits, int num);return ans;}
}编写完成主要的函数letterCombinations之后,就该编写回溯函数backtrack了。回忆括号生成问题中使用到的回溯函数backtrack,会发现回溯函数的主体依然为几个大的条件判断。括号生成问题中使用到的回溯函数backtrack分为三个if,分别处理:括号总数等于2*n,左括号数小于n,以及右括号数小于左括号数这三种情况。因此letterCombinations的主体也可以分为几个条件判断:combination字符串的长度等于digits长度、combination字符串长度小于digits长度。在括号生成的backtrack中,括号总数等于2*n时,通过push_back将当前字符串保存在ans中,所以在字母组合问题中当combination与digits长度相等时,也应该通过push_back将当前字符串保存在ans中。而在括号生成问题中,如果左括号数小于n,那么左括号入当前字符串,然后调用backtrack函数,调用完之后再从当前字符串中出一个括号。至于右括号数小于左括号数,也是类似的做法。所以在字母组合问题中,当combination长度小于digits长度时,应该通过for循环,将每一种数字对应的多个字母都尝试一次,将字母入字符串,然后调用backtrack函数,调用完之后从字符串出一个... ...因此,编写backtrack函数为:
void backtrack(vector<string>& ans, string& combination, string& digits, int num) {if(___________________________) {ans.push_back(combination);}else{for(char ch:_______________) {combination.push_back(ch);backtrack(ans, combination, digits, ____);combination.pop_back();}}
}4. (16. 最接近的三数之和)方法仍然是使用双指针。在处理之前,要先_______,以保证双指针的移动是逻辑上合理的。接着使用一个for循环外加判重,遍历第一个数字。在第一个数字已被确定的某一种情况之下,设置双指针,当三数之和sum减去target的差的绝对值比已有记录的差的最小绝对值还要小,就更新这个记录的差。接着移动双指针,如果sum大于target,那么左移右指针,如果sum小于target,那么右移左指针,而如果sum等于target,那么毫无疑问此时record已经为target,直接return返回即可。
5. (15. 三数之和)方法还是使用双指针。在处理之前,要先______,以保证双指针的移动在逻辑上是合理的。接着使用一个for循环外加判重,遍历第一个数字。在这里如果不判重,那么假如第一个数两次都是相同的,而双指针无法解决第一个数的重复问题,所以就会导致答案中出现两个一模一样的结果。另外除了判重之外,还可以仿照四数之和中的做法,如果第一个数和紧随其后的三个数还是大于0,那考虑到这时已经是从小排到大的已经排好的序列,再往后走已经没有意义,所以break即可,而如果第一个数和倒数第一、二个数的和还是小于0,那就说明第一个数还应该再往后走,即continue。在某一次的for循环之内,就要开始双指针的移动了。设置左指针为第一个数右边那个数,右指针为倒数第一个数,三数之和记作sum。如果sum等于0,就把此时三个数保存下来,然后左指针右移到与上一个数不同的地方,且右指针左移到与上一个数不同的地方。在这里如果只有一侧指针移动的话,显然是不合适的。而如果sum大于0或者小于0,只需要相应的左移右指针,与右移左指针即可,这时虽然会有重复,但是解决重复的目的是为了防止答案重复,而不是主要为了节省开销,所以不需要像for循环判重,以及像sum==0时那样解决掉判重问题。
6. (14. 最长公共前缀)有三种方法。第一种方法是,先找到前两个字符串的公共前缀,将其记录为commonprefix,接着再去找commonprefix和第__个字符串的公共前缀,再去找commonprefix和第__个字符串的公共前缀... ...具体是如何实现的呢?这里使用了函数__的概念。当传给函数longestCommonPrefix的参数只有一个vector<string>类型的变量strs时,其函数体的内容为:定义一个字符串commonprefix为strs[0],如果strs的大小为1,那么直接返回commonprefix,而如果strs的大小大于1,则通过一个for循环来依次求出来最长公共前缀,for(int i = 0; i < len; i++)循环,依次让commonprefix = longestCommonPrefix(commonprefix, strs[i]); 最终返回commonprefix,其中len为______。当传给函数longestCommonPrefix的参数是两个string类型的变量str1与str2时,其函数体的内容为:定义一个字符串commonprefix,它是空串,求出两个串的最小长度len,for(int i = 0; i < len; i++),循环体的内容是:___________________。
7. (14. 最长公共前缀)三种方法里面的第二种方法。依次比较所有字符串的第一个字符是否相同、第二个字符是否相同、第三个字符是否相同... ...代码如下,补全代码:
class Solution {
public:string longestCommonPrefix(vector<string>& strs) {int strslen = strs.size();int minlen = strs[0].size();string commonprefix =_____;for(int i = 0; i < strslen; i++) {minlen = minlen < strs[i].size()?______:______;}for(int i = 0; i < minlen; i++) {char ch =_____;int j = 0;for(; j < strslen; j++) {if(strs[_][_] != ch) {return _________;}else{continue;}}if(j == _______) commonprefix.push_back(ch);}return commonprefix;}
};相关文章:
)
2024.03.04——2024.03.10 力扣练习总结及专项巩固(二)
1. (22. 括号生成)这里只讨论第二种做法回溯法。在回溯法的函数void backtrack(vector<string>& ans, string& current, int open, int close, int n); 中,可分为三个if条件判断,分别判断当current.size() 2*n,ope…...

前端NodeJs笔记之包结构到进程和线程到命令行到Node模块化讲解
包结构 包实际上是一个压缩文件,解压以后还原为目录,符合规范的目录应该包含如下文件: -package.json 描述文件 -bin 可执行二进制文件 -lib js代码 -doc …...

【Java】获取手机文件名称补充
本地的 ADB 工具路径指的是你电脑上安装的 Android Debug Bridge(ADB)工具的路径。ADB 是 Android SDK 中的一个工具,用于与连接到计算机上的 Android 设备进行通信。你需要确保 ADB 已正确安装,并知道其在你计算机上的位置。 通…...

YoloV8改进策略:BackBone改进|TransNeXt:ViT的鲁棒Foveal视觉感知
文章目录 摘要论文:《TransNeXt:ViT的鲁棒Foveal视觉感知》1、引言2、相关工作3、方法3.1、聚合像素焦点注意力3.1.1、像素焦点注意力3.1.2、在单个混合器中聚合不同的注意力3.1.3、克服多尺度图像输入3.1.4、特征分析3.2、卷积门控单元(Convolutional GLU)3.2.1、动机3.2.…...

三维的旋转平移矩阵形式
在三维空间中,一个物体或坐标系的旋转和平移可以通过一个4x4的变换矩阵来表示。这个矩阵通常被称为仿射变换矩阵或齐次变换矩阵。它结合了旋转矩阵和平移向量的功能,能够同时表示旋转和平移操作。 一个4x4的旋转平移矩阵通常具有以下形式: 复…...

ChatGPT+MATLAB应用
MatGPT是一个由chatGPT类支持的MATLAB应用程序,由官方Toshiaki Takeuchi开发,允许您轻松访问OpenAI提供的chatGPT API。作为官方发布的内容,可靠性较高,而且也是完全免费开源的,全程自己配置,无需注册码或用…...

C语言—冒泡排序
C语言—冒泡排序 原理过程讲解代码1、直接在主函数里面实现2、编写函数进行实现 原理 冒泡排序的原理是:从左到右,相邻元素进行比较。每次比较一轮,就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。 以从小到大排序…...
Discord OAuth2授权以及机器人监听群事件
下面文章讲解获取OAuth2授权整个流程,创建机器人,使用机器人监听工会(工会就是创建的服务器)成员变化等等,对接国外的都是需要VPN的哦,对接的时候记得提前准备。 创建应用 点击 此页面添加应用,ÿ…...

微信小程序返回上一页刷新组件数据
在父页面的onShow和onHide里面添加一个标志 onShow() {this.setData({show:true})},onHide() {this.setData({show:false})}, 把这个值传给子组件 <importantList slot"importantConcern" flag"{{barSelect}}" flag2"{{show}}" /> 在子组…...
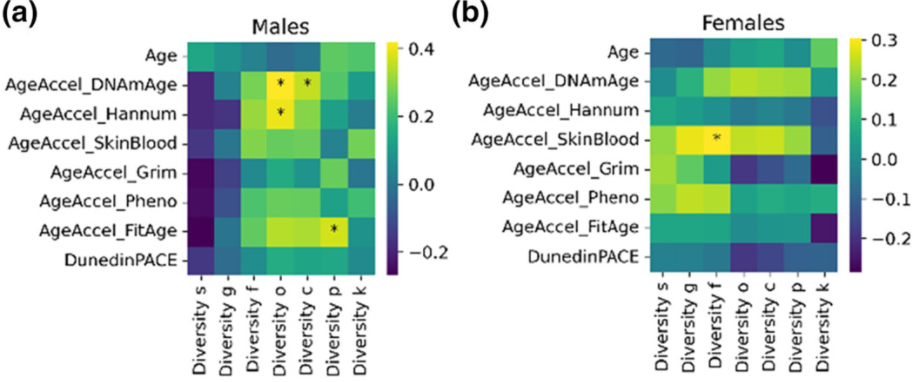
Aging Cell:匈牙利学者发现肠道微生物组的变化和衰老密切相关
基于DNA甲基化衰老时钟的开发可以准确用来测量生物年龄,生物年龄在很大程度上受生活方式、环境和遗传等因素的影响,大量证据也表明健康生活方式可以延缓衰老并延长寿命。 先前大规模微生物组分析表明,随着年龄的增长,微生物组菌群…...
)
837. 连通块中点的数量(acwing)
文章目录 837. 连通块中点的数量题目描述维护size的并查集 837. 连通块中点的数量 题目描述 给定一个包含 n 个点(编号为 1~n)的无向图,初始时图中没有边。 现在要进行 m 个操作,操作共有三种: C a b&a…...
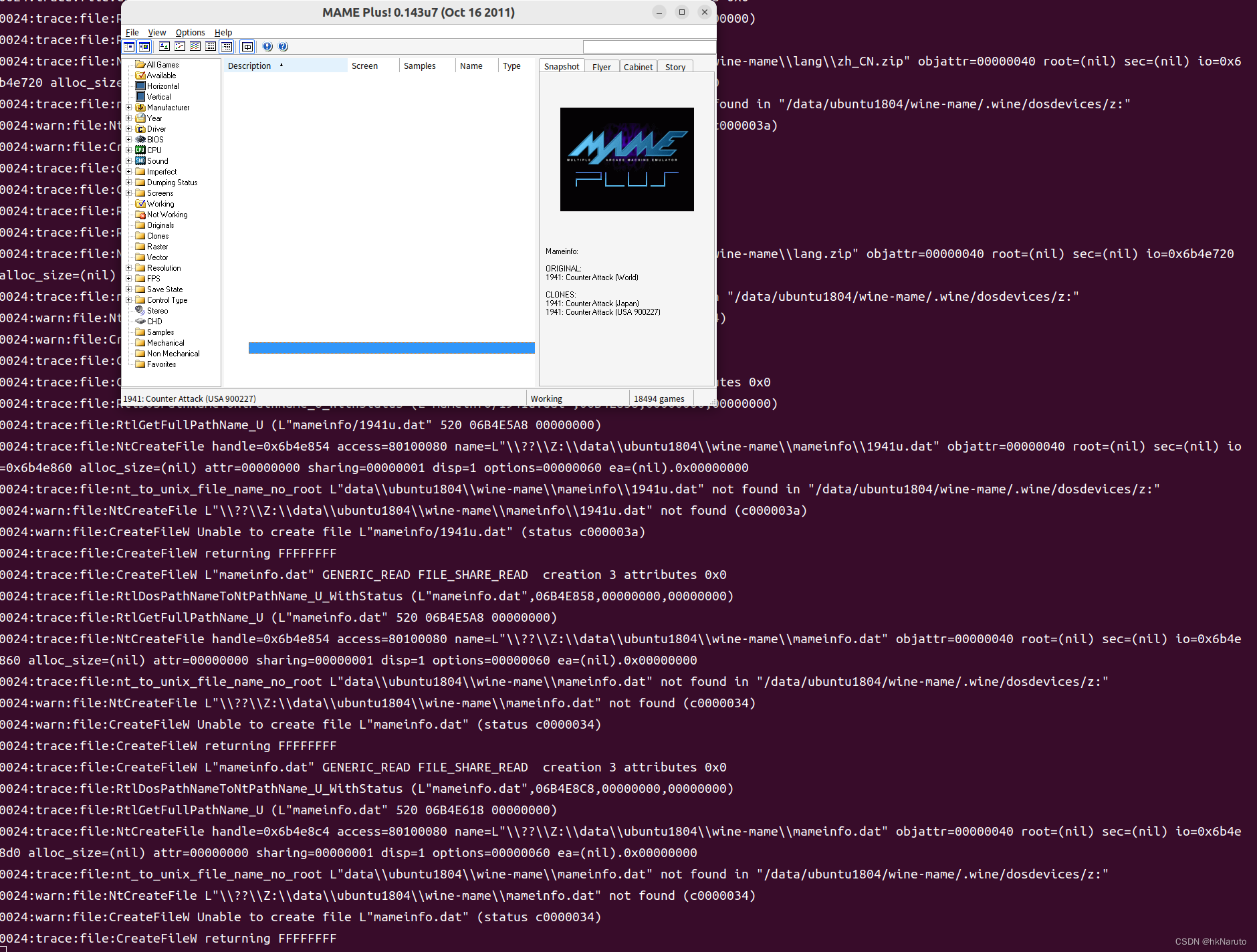
【wine】WINEDEBUG 分析mame模拟器不能加载roms下面的游戏 可以调整参数,快速启动其中一个游戏kof98
故障现象,MAME启动后,游戏都没有识别 添加日志输出,重新启动wine #!/bin/bashexport WINEPREFIX$(pwd)/.wine export WINESERVER$(pwd)/bin/wineserver export WINELOADER$(pwd)/bin/wine export WINEDEBUG"file,mame,warn,err"…...

pytorch安装记录
pytorch安装记录 1 安装anconda2 安装pycharm3 安装显卡驱动4 根据显卡驱动版本下载CUDA5 cudnn安装6 根据CUDA版本安装pytorch7 pytorch卸载 1 安装anconda 下载地址: https://www.anaconda.com/download#downloads 验证是否安装成功:打开cmd, 输入 conda 验证环…...

不依赖第三方平台,用Dart语言实现 ios 消息推送
仅仅给大家提供代码,还搞不定的欢迎咨询。 void _sendIosPushNotification(BleMessage message, String deviceToken, {bool debugMode = false}) async {final Map<String, dynamic> header = {"alg": "ES256", "kid": GloabelConfigu…...

TEASEL: A transformer-based speech-prefixed language model
文章目录 TEASEL:一种基于Transformer的语音前缀语言模型文章信息研究目的研究内容研究方法1.总体框图2.BERT-style Language Models(基准模型)3.Speech Module3.1Speech Temporal Encoder3.2Lightweight Attentive Aggregation (LAA) 4.训练…...
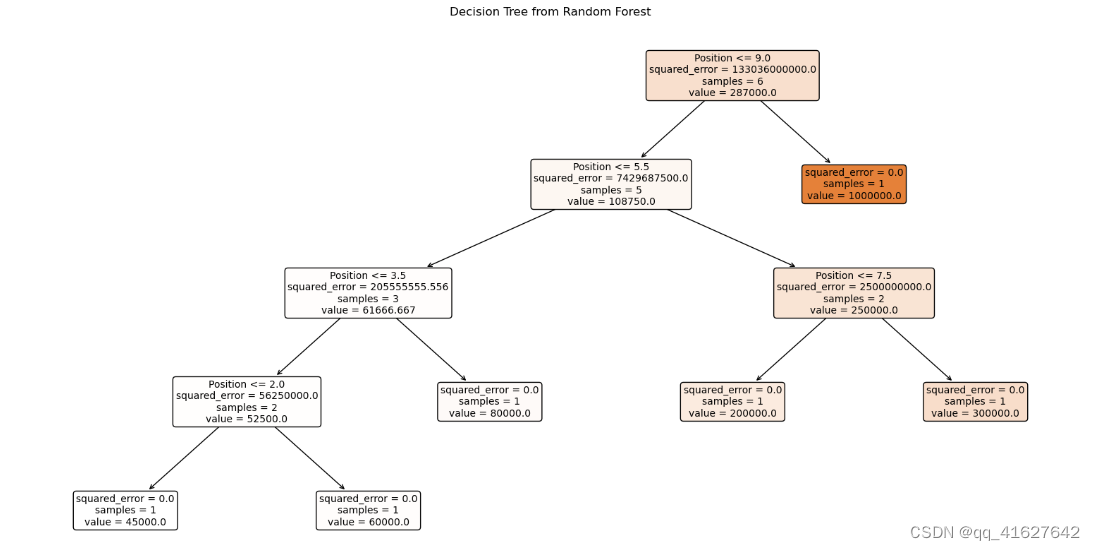
机器学习之分类回归模型(决策数、随机森林)
回归分析 回归分析属于监督学习方法的一种,主要用于预测连续型目标变量,可以预测、计算趋势以及确定变量之间的关系等。 Regession Evaluation Metrics 以下是一些最流行的回归评估指标: 平均绝对误差(MAE):目标变量的预测值与实际值之间的平均绝对差…...

算法二刷day3
203.移除链表元素 class Solution { public:ListNode* removeElements(ListNode* head, int val) {ListNode *dummyHead new ListNode(0);dummyHead->next head;ListNode *cur dummyHead;while (cur->next ! nullptr) {if (cur->next->val val) {ListNode *tm…...
面具安装LSP模块时提示 Unzip error错误的解决办法
面具(Magisk Delta)安装LSP模块时提示 Unzip error错误的解决办法 如果前面的配置都正常的话,可能是LSP版本有问题重新去Github下载一个最新版的吧;我是这么解决的。 我安装1.91那个版本的LSP就是死活安装不上,下载了1.92的版本一次就…...

HarmonyOS 关系型数据 整体测试 进行 初始化 增删查改 操作
好啊 前面的文章 HarmonyOS 数据持久化 关系型数据库之 初始化操作 HarmonyOS 数据持久化 关系型数据库之 增删改逻辑编写 HarmonyOS 数据持久化 关系型数据库之 查询逻辑编写 我们分别编写了 初始化数据库表 增删查改操作 的逻辑代码 那么 下面我们就来整体操作一下 然后 这…...
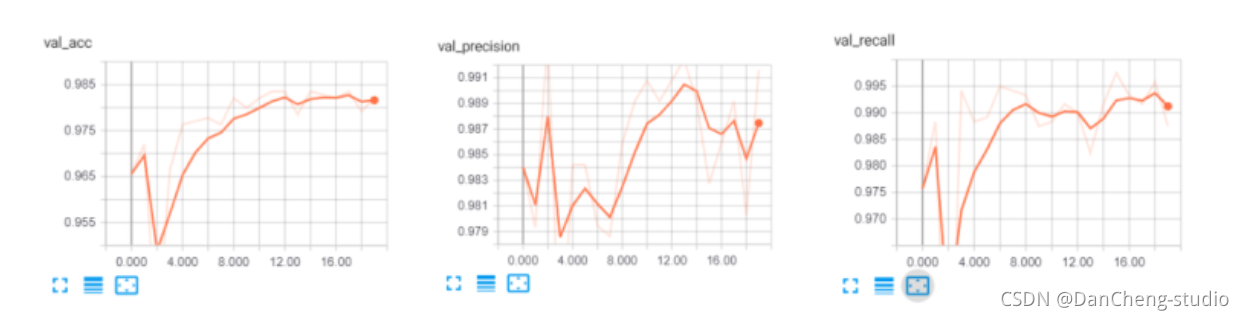
软件杯 垃圾邮件(短信)分类算法实现 机器学习 深度学习
文章目录 0 前言2 垃圾短信/邮件 分类算法 原理2.1 常用的分类器 - 贝叶斯分类器 3 数据集介绍4 数据预处理5 特征提取6 训练分类器7 综合测试结果8 其他模型方法9 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 垃圾邮件(短信)分类算…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...
