【机器学习300问】33、决策树是如何进行特征选择的?
还记得我在【机器学习300问】的第28问里谈到的,看决策树的定义不就是if-else语句吗怎么被称为机器学习模型?其中最重要的两点就是决策树算法要能够自己回答下面两问题:
- 该选哪些特征 == 特征选择
- 该选哪个阈值 == 阈值确定
今天这篇文章承接上文,继续深入的讲讲决策树是如何进行特征选择的?如果没有看上篇文章的友友可以点个链接哦:
【机器学习300问】28、什么是决策树?![]() http://t.csdnimg.cn/Tybfj
http://t.csdnimg.cn/Tybfj
一、看一个猫咪二分类的例子
假设你正在教一群小朋友在公园里快速分辨出哪些动物是猫,哪些是狗。现在你们面前有一大堆动物的照片,每张照片都包含了三个特征,比如“耳朵形状”、“脸是不是圆的”、“有没有胡须”。让我们试着用决策树算法来构造一颗树,先只构造根节点和左右子树。
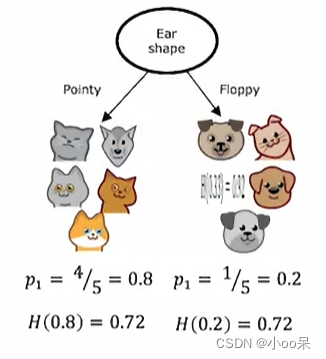
选择耳朵是竖起来还是塌下去这个特征,我们把10个样本分成了两个子树。图中p代表猫猫出现的概率(或占比),H是信息熵函数。
二、什么是信息熵?
首先,我们得理解信息熵的概念,信息熵是衡量一个随机变量不确定性的度量。就像孩子们开始时对所有照片的不确定性。如果照片中猫和狗的数量各占一半,那么不确定性最高,就好比每个小朋友随机猜的话,正确率只有50%。这个不确定性可以用数学上的熵来量化:
其中 表示数据集,
是类别
出现的概率。如果还是有点困惑的话,我们画一个图并配合一些例子来进一步解释信息熵的概念。
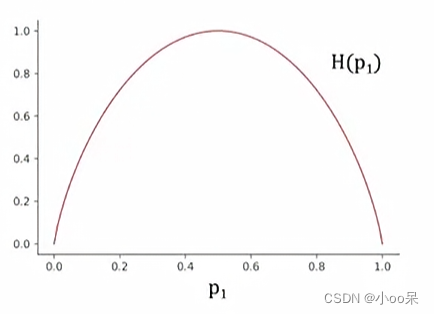
(1)p=0.5 H=1的情况
这张图是信息熵的曲线图,可以看到在p=0.5的时候,信息熵最大意味着此时对于这张图片是猫咪还是小狗最不确定。也就是说是猫的可能性为50%,是狗的可能性也是50%
(2)p=0.83 H=0.65的情况
假设p=0.83图中可以看出H(0.8)=0.65,这种情况是说,6个动物图片中有5个是小猫1个是小狗,那么我比较有把握的说和这6张图片类似的动物图片,我蛮确定它是小猫,有多确定它是小猫呢?有0.65的确定性。
(3)p=1 H=0的情况
假设p=1,从图中可以看出H=0,这种情况是说按照某种特征来区分猫狗,分出来一边全是猫咪,一边全是小狗,这意味着数据集中的不确定性最小(不确定性为零)
(4)总结一下什么是信息熵
- 信息熵是衡量一个随机变量不确定性的度量
- 当某个事件发生完全确定时(概率为1或0),信息熵为0
- 当事件发生的不确定性最高,所有可能结果的概率相同时,对于二元事件(如猫狗分类),信息熵达到最大值1
三、什么是信息增益?
简单说信息增益就是划分前的信息熵减去条件熵,表示使用该特征后不确定性减少的程度。
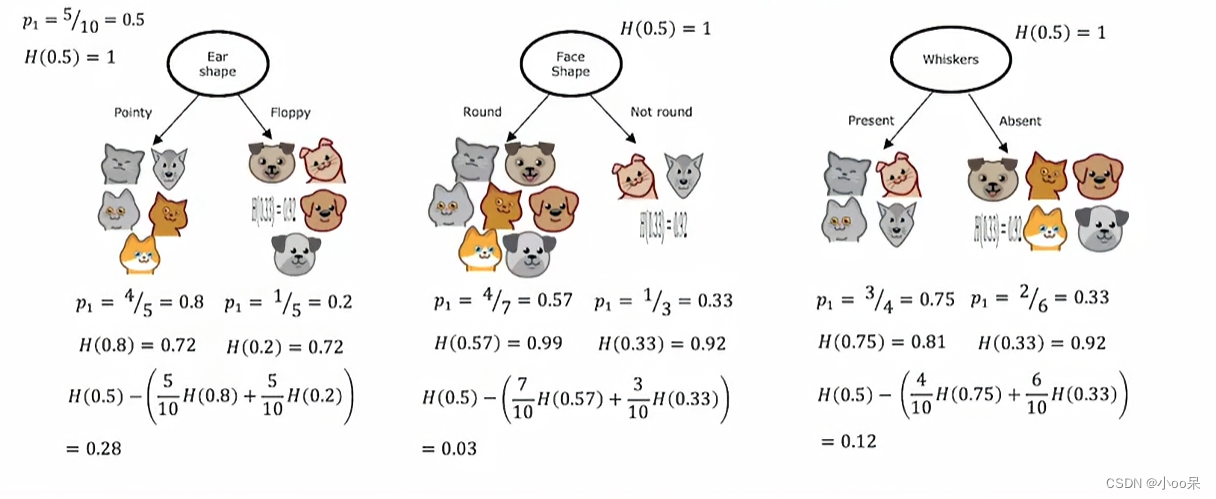
(1)加权平均信息熵
在图3中,用耳朵的形状进行划分后,左右两个子树的信息熵可以单独被计算出来,一个是H(0.8)=0.72另一个是H(0.2)=0.72,这两个数代表了两个子树他们的不确定性,可是我现在想知道的是用耳朵的形状进行划分这种策略所到账的不确定性。所以我可以使用加权平均的方法将左右两个合在一起计算得到这种特征用于根节点决策所导致不确定性:
其中的就是权重,w具体是指子树的样本数量占总样本数量的比例,p具体是指猫出现在子树中的概率。这样我们就得到了采取某种特征进行分类的策略会导致多少不确定性。才能判断出这个特征选的好不好。
(2)信息增益公式
但这还不够,因为我们要思考这个策略好不好,主要不是看当下的H值,而是看他相较于上一次减少了多少不确定性,这样做更有利于我们判断到底选哪个特征做根节点好,所以我们得用前一次的不确定性减去这一次的不确定性,得出来的就是信息增益(根节点):
写成更一般(任意决策节点)的公式就是:
| 符号 | 含义 |
| 表示在给定特征 f 的条件下,数据集D的信息增益 | |
| 数据集的原始信息熵 | |
| 子集大小占总数据集大小的比例 | |
| 子集的信息熵 |
四、决策树是如何进行特征选择的?
具体选择的流程:
- 计算划分前的数据集熵(即原始不确定性)。
- 对于每一个特征,比如“耳朵形状”,按照这个特征把数据集划分为不同的子集。
- 分别计算每个子集的信息熵,并根据子集内样本数目的比例加权求和。
- 计算出信息增益,信息增益就是划分前的熵减去条件熵,表示使用该特征后不确定性减少的程度。
- 对比每一个特征计算出来的信息增益,选择那个信息增益最大的特征!
相关文章:
【机器学习300问】33、决策树是如何进行特征选择的?
还记得我在【机器学习300问】的第28问里谈到的,看决策树的定义不就是if-else语句吗怎么被称为机器学习模型?其中最重要的两点就是决策树算法要能够自己回答下面两问题: 该选哪些特征 特征选择该选哪个阈值 阈值确定 今天这篇文章承接上文&…...

剑指offer C ++双栈实现队列
1. 基础 队列:先进先出,即插入数据在队尾进行,删除数据在队头进行; 栈:后进先出,即插入与删除数据均在栈顶进行。 2. 思路 两个栈实现一个队列的思想:用pushStack栈作为push数据的栈ÿ…...

【YOLOv9】训练模型权重 YOLOv9.pt 重新参数化轻量转为 YOLOv9-converted.pt
【YOLOv9】训练模型权重 YOLOv9.pt 重新参数化轻量转为 YOLOv9-converted.pt 1. 模型权重准备2. 模型重新参数化2.1 文件准备2.2 参数修改2.3 重新参数化过程 3. 重新参数化后模型推理3.1 推理超参数配置3.2 模型推理及对比 4. onnx 模型导出(补充内容)4…...

Zookeeper搭建
目录 前言 初了解Zookeeper 搭建 准备 配置Zookeeper 前言 今天来介绍Zookeeper的搭建,其实Zookeeper的搭建很简单,但是为什么还要单独整一节呢,这就不得不先了解Zookeeper有什么功能了!而且现在很火的框架也离不开Zookeepe…...
2.Datax数据同步之Windows下,mysql和sqlserver之间的自定义sql文数据同步
目录 前言步骤操作大纲步骤明细mysql 至 sqlServersqlServer 至 mysql执行同步语句中报 前言 上一篇文章实现了不同的mysql数据库之间的数据同步,在此基础上本篇将实现mysql和sqlserver之间的自定义sql文数据同步 准备工作: JDK(1.8以上,推…...

commonjs和esmodule
commonjs的模块导出和引用写法: lib.js 导出一个模块 let a 1 let b 2 function aPlus1() {return a } module.exports {a,b,aPlus1 } index.js引用一个模块 const {a,b,aPlus1} require(./lib.js) console.log(hh:,a) esmodule的模块导出和引用方法&#x…...

Android的编译系统
安卓的编译真的太多吐槽的地方了,有必须到croot下编译的,有随便改个.c就要七八分钟编译的。我有时候真的不知道这么多开发人员是怎么挺过来的。 今晚简单看看这个编译系统soong吧。 算了,下面这个写的很好了,我先看看吧。。。 …...

Midjourney指控Stability AI夜袭数据,网络风波一触即发
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
JVM知识整体学习
前言:本篇没有任何建设性的想法,只是我很早之前在学JVM时记录的笔记,只是想从个人网站迁移过来。文章其实就是对《深入理解JVM虚拟机》的提炼,纯基础知识,网上一搜一大堆。 一、知识点脑图 本文只谈论HotSpots虚拟机。…...

蓝桥杯--日期统计
目录 一、题目 二、解决代码 三、代码分析 四、另一种思路 五、关于set文章推荐 一、题目 二、解决代码 #include <bits/stdc.h> using namespace std; int main() {int arr[100] { 5,6,8,6,9,1,6,1,2,4,9,1,9,8,2,3,6,4,7,7,5,9,5,0,3,8,7,5,8,1,5,8,6,1,8,3,0,…...
[leetcode~dfs]1261. 在受污染的二叉树中查找元素
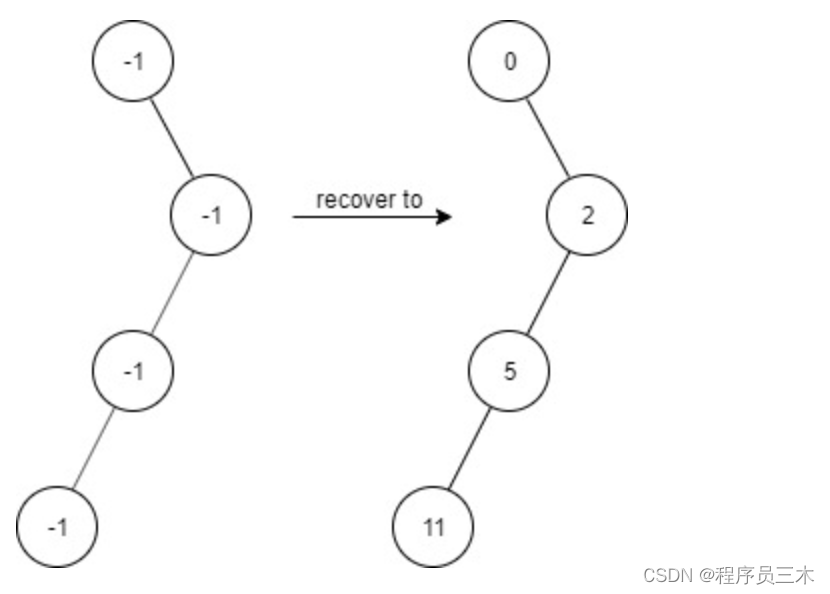
给出一个满足下述规则的二叉树: root.val 0 如果 treeNode.val x 且 treeNode.left ! null,那么 treeNode.left.val 2 * x 1 如果 treeNode.val x 且 treeNode.right ! null,那么 treeNode.right.val 2 * x 2 现在这个二叉树受到「污…...
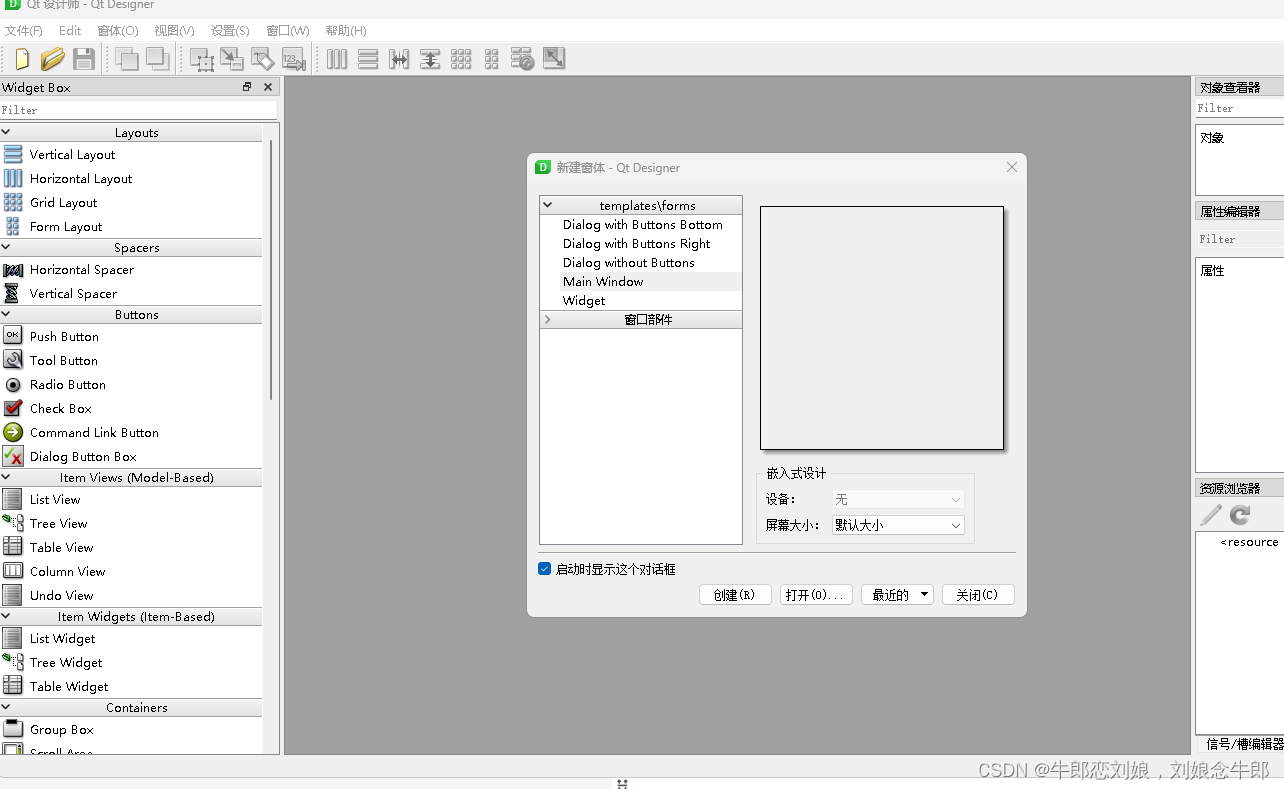
PyQt5使用
安装Pyqt5信号与槽使用可视化界面编辑UI (Pyside2)ui生成之后的使用(两种方法)1 ui转化为py文件 进行import2 动态调用UI文件 安装Pyqt5 pip install pyqt5-tools这时候我们使用纯代码实现一个简单的界面 from PyQt5.QtWidgets import QApplication, QMainWindow, QPushButto…...

利用GPT开发应用005:Codex、Turbo、ChatGPT、GPT-4
文章目录 一、GPT-3 Codex二、GPT-3.5 Turbo二、ChatGPT三、GPT-4 一、GPT-3 Codex 2022年3月,OpenAI 发布了 GPT-3 Codex 的新版本。 这个新模型具有编辑和插入文本的能力。它们是通过截至 2021 年 6 月的数据进行训练的,并被描述为比之前版本更强大。到…...
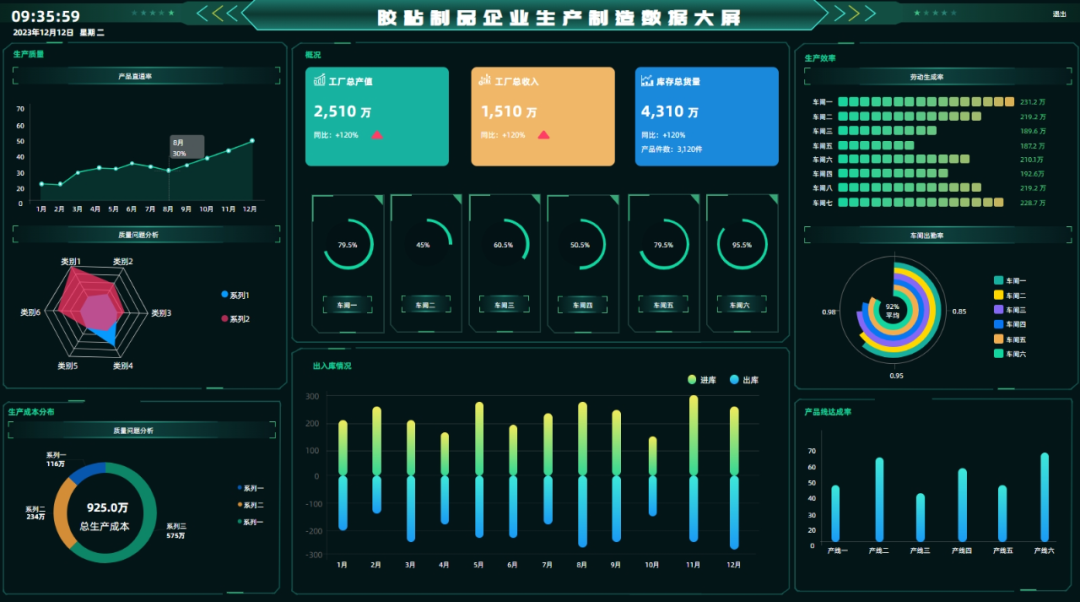
制造行业大数据应用:四大领域驱动产业升级与智慧发展
一、大数据应用:制造行业的智慧引擎 随着大数据技术的不断突破与普及,制造行业正迎来一场前所未有的变革。大数据应用,如同智慧引擎一般,为制造行业注入了新的活力,推动了产业升级与创新发展。 二、大数据应用在制造行…...
25.5 MySQL 聚合函数
1. 聚合函数 聚合函数(Aggregate Function): 是在数据库中进行数据处理和计算的常用函数. 它们可以对一组数据进行求和, 计数, 平均值, 最大值, 最小值等操作, 从而得到汇总结果.常见的聚合函数有以下几种: SUM: 用于计算某一列的数值总和, 可以用于整数, 小数或者日期类型的列…...

多维时序 | Matlab实现VMD-CNN-LSTM变分模态分解结合卷积神经网络结合长短期记忆神经网络多变量时间序列预测
多维时序 | Matlab实现VMD-CNN-LSTM变分模态分解结合卷积神经网络结合长短期记忆神经网络多变量时间序列预测 目录 多维时序 | Matlab实现VMD-CNN-LSTM变分模态分解结合卷积神经网络结合长短期记忆神经网络多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介…...

用Python进行机器学习:Scikit-learn的入门与实践【第126篇—Scikit-learn的入门】
用Python进行机器学习:Scikit-learn的入门与实践 随着机器学习在各个领域的广泛应用,Python成为了一个备受欢迎的机器学习工具之一。在众多机器学习库中,Scikit-learn因其简单易用、功能强大而备受青睐。本文将介绍Scikit-learn的基本概念&am…...

2024年G3锅炉水处理证模拟考试题库及G3锅炉水处理理论考试试题
题库来源:安全生产模拟考试一点通公众号小程序 2024年G3锅炉水处理证模拟考试题库及G3锅炉水处理理论考试试题是由安全生产模拟考试一点通提供,G3锅炉水处理证模拟考试题库是根据G3锅炉水处理最新版教材,G3锅炉水处理大纲整理而成࿰…...

常用的gpt网站
ChatGPT是一款基于人工智能技术的对话型AI助手,能够进行自然语言交互并提供个性化的对话服务。通过先进的深度学习模型,ChatGPT能够理解用户输入的文本,并生成有逻辑、连贯性的回复。它可以回答各种问题、提供建议、分享知识,还能…...

java中string类型常用的37个函数
java中string类型常用的37个函数—无极低码 int indexOf(int ch, int fromIndex) 、int indexOf(int ch) 、int indexOf(String str, int fromIndex) 、int indexOf(String str) 、int lastIndexOf(int ch, int fromIndex) 、int lastIndexOf(int ch) 、int lastIndexOf(Strin…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
