使用Docker管理linux容器
文章目录
一、使用docker管理镜像
二、使用docker管理容器
一、使用docker管理镜像
1、安装操作系统,我安装的是centOS 7 ,因为centos7有着非常丰富的软件仓库,方便后续安装与docker相关的软件。

2、初始化设置,
关闭防火墙
关闭selinux
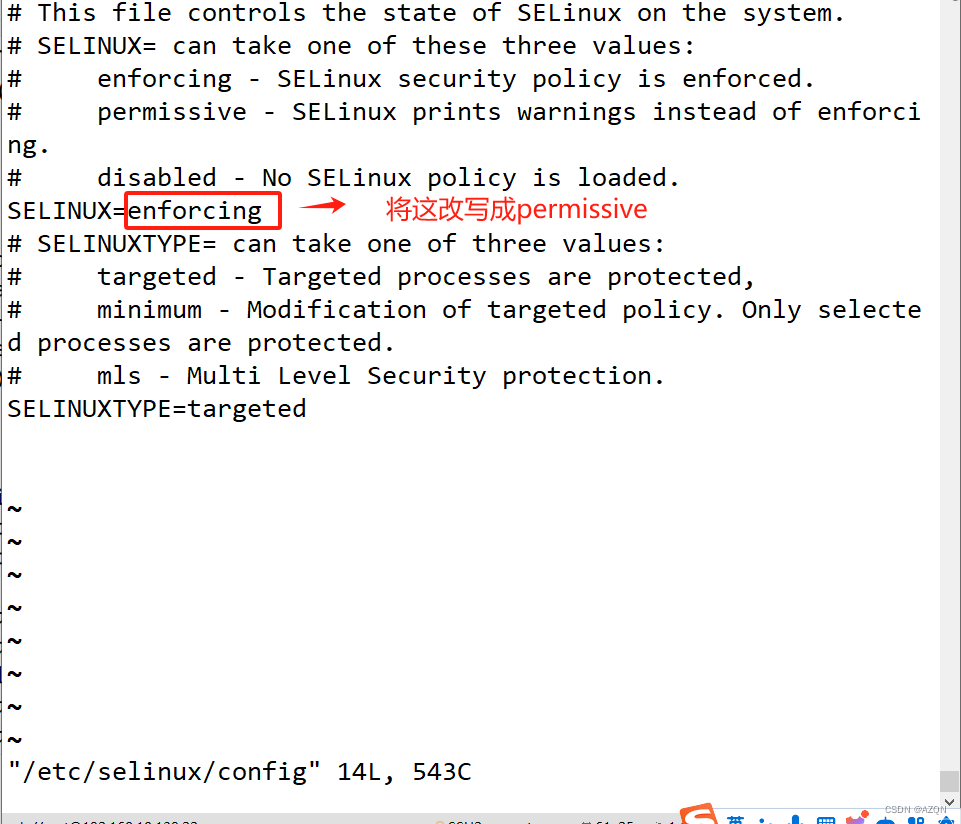
重启生效

使用gentenforce命令查看selinux状态
2、配置IP地址,让网络能上网。
3、安装docker
4.启动并配置docker开机自启动

5、查看镜像
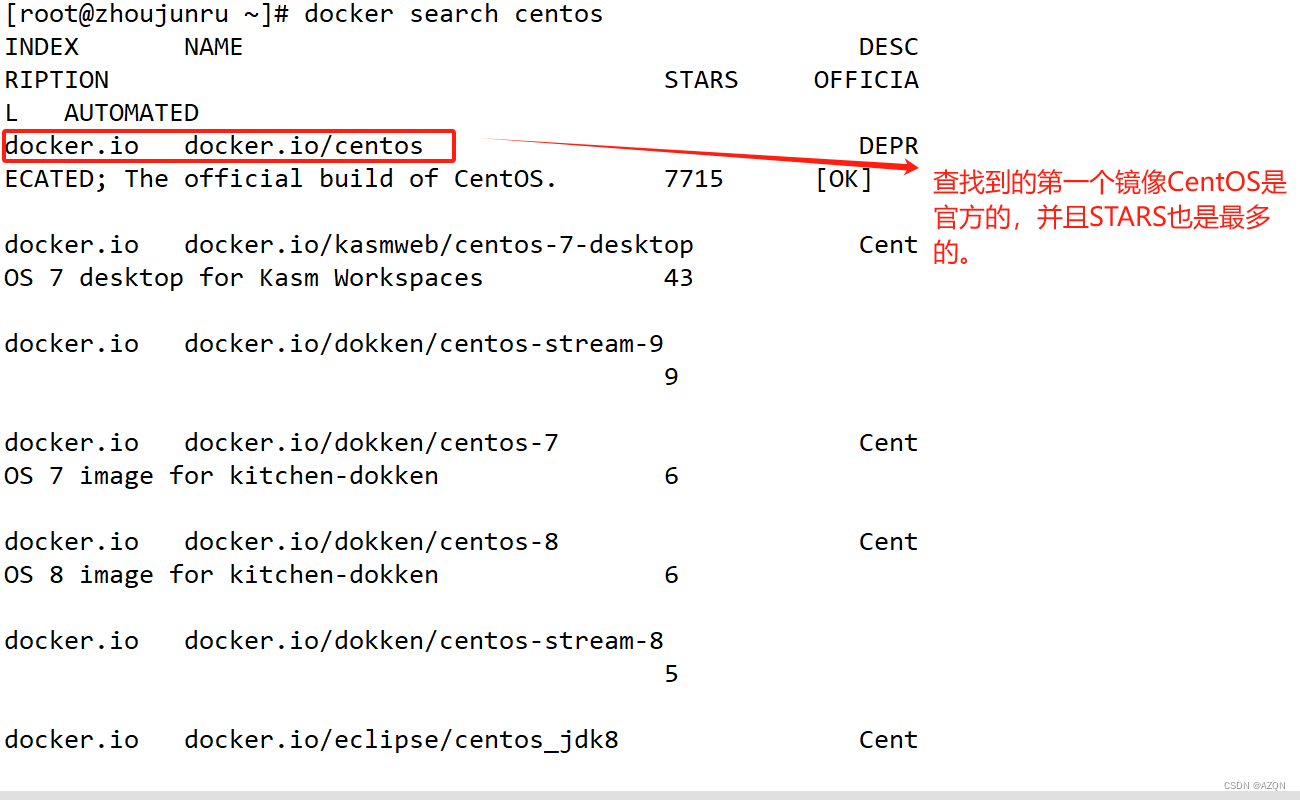
6.从仓库里拉取镜到本地。拉取镜像是获取软件是意思,镜像是用于创建容器的一种环境
情景一:成功拉取到镜像

情景二:因为镜像是在Docker HUB上,由于Docker HUB 的服务器在境外,访问很慢,因此在拉镜像是出现超时。
由于一些原因,国内下载Docker HUB 官方镜像的速度比较慢,可以使用DaocCloud镜像加速。
然后按照DaoCloud上面说的方式,将镜像拉回本地,再查看本地镜像。

7.给镜像改名字。

8、删除刚拉下来的镜像daocloud.io/centos

二、使用docker管理容器
镜像已经拉到本地,需要把镜像运行起来。当镜像运行起来时,那么此时镜像就是一个容器。
1、运行一个镜像

2.再次运行镜像.因为容器退出后不会再继续运行,所以运行镜像时,我们需要加上的参数让容器退出后也能一直运行。

3.进入容器

4、查看容器I的P地址

安装net-tools工具包

安装iproute工具包

此时看到容器的IP地址为B类地址172.17.0.2/16
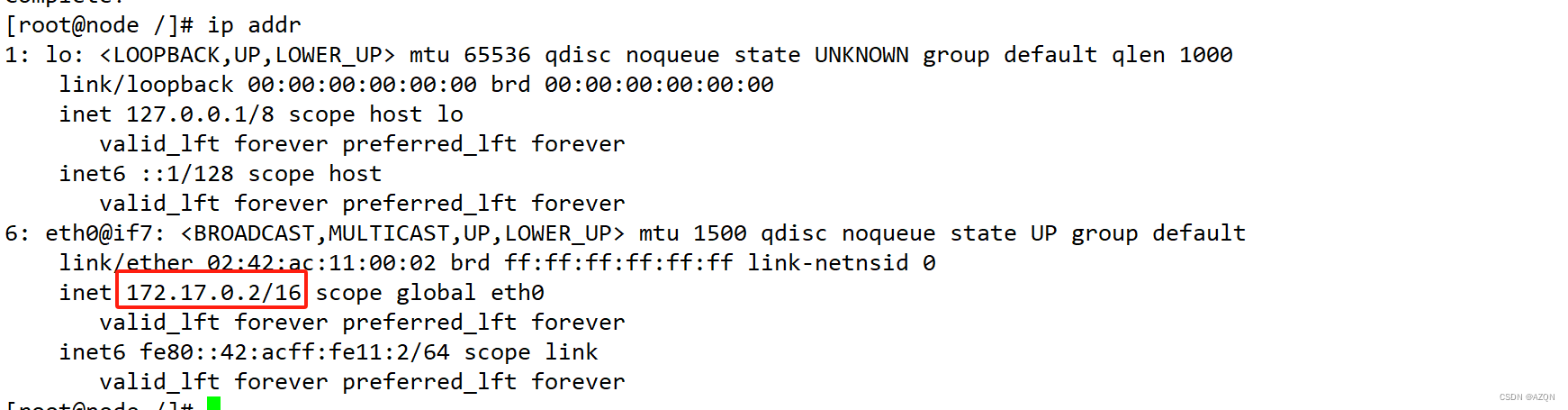
5.安装httpd服务程序并且启动httpd服务。

在容器内部,httpd命令可以启动Apache HTTP服务器服务,但是在容器中使用systemctl start httpd命令无法正常工作的原因:systemctl命令需要与操作系统的初始化系统(如 systemd)进行交互,以启动、停止或管理系统服务。然而,容器通常没有运行完整的操作系统,因此缺少必要的组件和权限,无法使用 systemctl命令。
在容器内启动Apache HTTP服务器,可以直接执行httpd命令,它会以非系统服务的方式启动。这种方式适用于容器化环境,因为容器通常专注于单个应用程序或服务,而不需要完整的操作系统服务管理功能。
6 .在服务器的首页index.h
![]()
7.在主机上测试是否可以访问到容器提供的httpd服务。
宿主机的IP地址为192.168.10.139/24
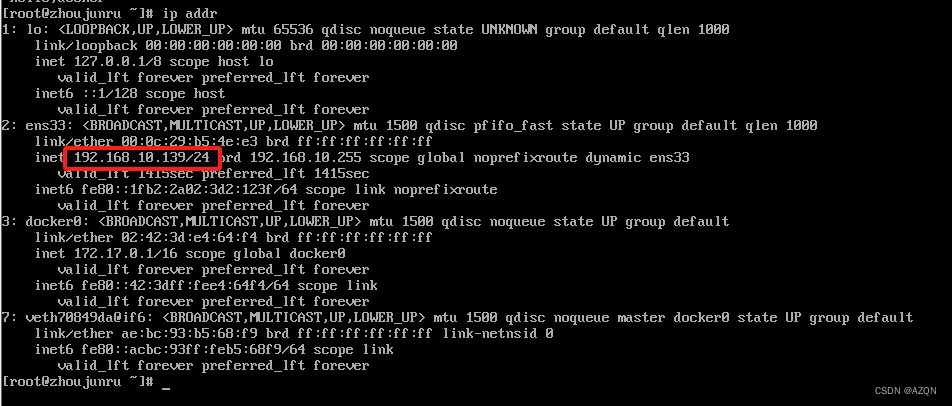

相关文章:

使用Docker管理linux容器
文章目录 一、使用docker管理镜像 二、使用docker管理容器 一、使用docker管理镜像 1、安装操作系统,我安装的是centOS 7 ,因为centos7有着非常丰富的软件仓库,方便后续安装与docker相关的软件。 2、初始化设置, 关闭防火墙 关闭…...
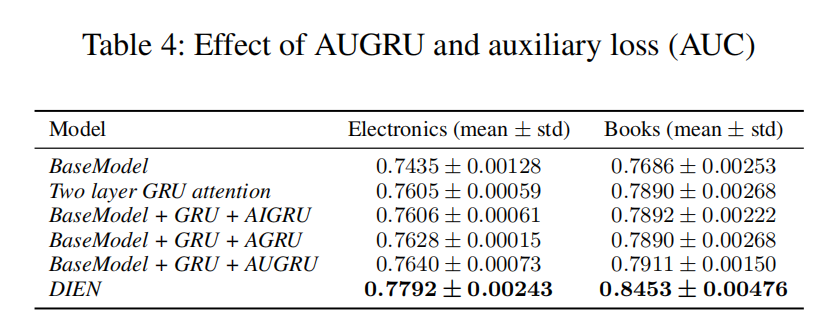
CTR之行为序列建模用户兴趣:DIEN
前言 在上一篇文章中 CTR之行为序列建模用户兴趣:DIN,开启了用户行为序列建模用户兴趣的篇章。DIN引入了Attention机制,对于不同的候选item,可以根据用户的历史行为序列,动态地学习用户的兴趣表征向量。但是ÿ…...
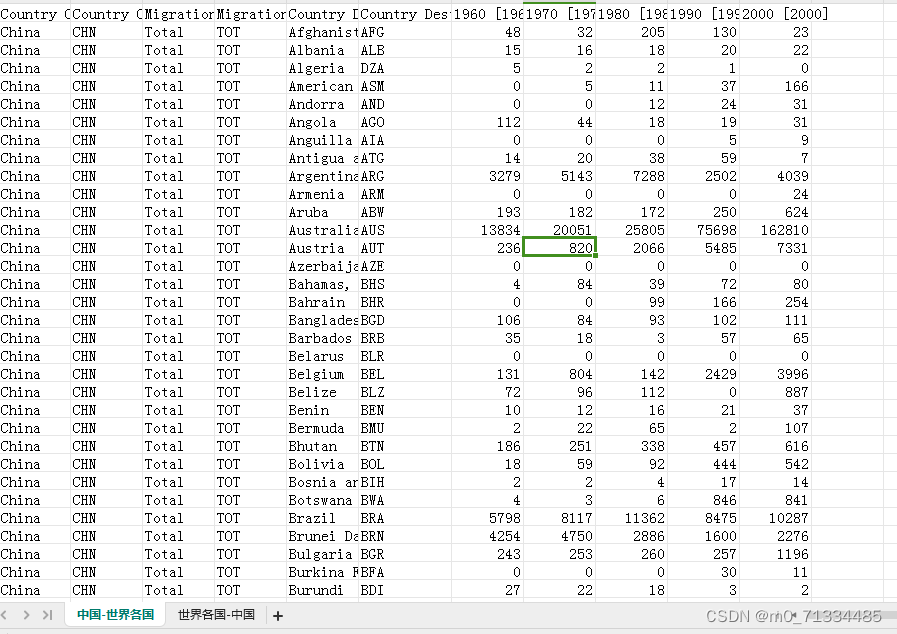
1960-2020年全球双边迁移数据库(Global Bilateral MigrationDatabase)
1960-2020年全球双边迁移数据库(Global Bilateral MigrationDatabase) 1、时间:1960-2000年,每10年一次具体为:1960年、1970年、1980年、1990年、2000年 2、来源:世界银行 3、指标:Country O…...

OpenGL-贴纸方案
OpenGL-贴纸方案 普通贴纸(缩放、Z轴旋转、平移) OpenGL环境说明 OpenGL渲染区域使用正交投影换算,正常OpenGL坐标是vertexData,这样的 Matrix.orthoM 进行换算 //顶点坐标(原点为显示区域中心店)private final float[] vertex…...
【性能测试】移动测试md知识总结第1篇:移动端测试课程介绍【附代码文档】
移动测试完整教程(附代码资料)主要内容讲述:移动端测试课程介绍,移动端测试知识概览,移动端测试环境搭建,ADB常用命令学习主要内容,学习目标,学习目标,1. window安装andorid模拟器,学习目标。主流移动端自动…...
)
Vue2和vue3的区别(前端面试常见问题)
1.Api的变化:vue3使用组合式Api(compostion Api)和Vue2是选项式Api(options Api)。选项式Api具有data ,watch,methods,computed,一个个的模块。如果代码过多可读性会很差…...

openGauss学习笔记-241 openGauss性能调优-SQL调优-审视和修改表定义
文章目录 openGauss学习笔记-241 openGauss性能调优-SQL调优-审视和修改表定义241.1 审视和修改表定义概述241.2 选择存储模型241.3 使用局部聚簇241.4 使用分区表241.5 选择数据类型 openGauss学习笔记-241 openGauss性能调优-SQL调优-审视和修改表定义 241.1 审视和修改表定…...
)
PDFPlumber解析PDF文本报错:AssertionError: (‘Unhandled’, 6)
文章目录 1、问题描述2、问题原因3、问题解决 1、问题描述 今天在使用PDFPlumber模块提取PDF文本时extract_text()方法报错,报错内容如下: Traceback (most recent call last):......File "F:\Python\...\site-packages\pdfminer\pdffont.py"…...

51WORLD正式落地中东,助力沙特伙伴与客户数字化升级!
近日,在被誉为中东“数字达沃斯”的LEAP科技展上,51WORLD首次震撼亮相Digital Twin Riyadh2924k㎡ 全要素城市底座、数字地球平台51Earth,向中东及全球科技从业者展现中国企业技术实力与创新能力。此外,以LEAP为起点,5…...
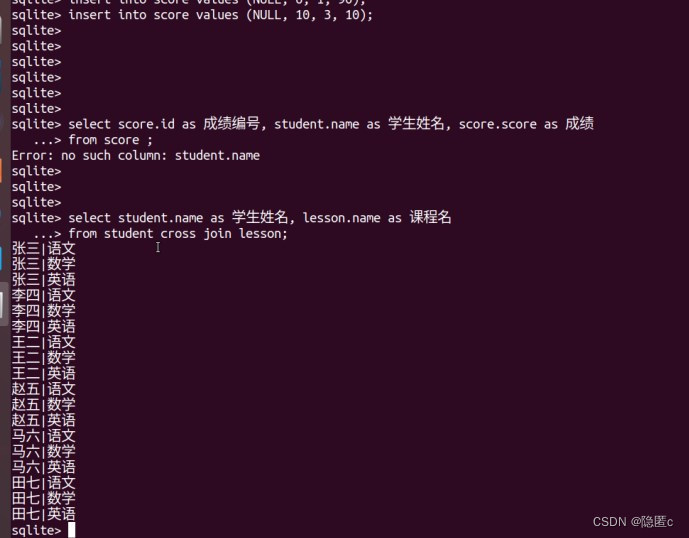
嵌入式学习38-数据库
数据库软件: 关系型数据库: Mysql (开源) Oracle SqlServer Sqlite (小型数据) 非关系型数据库:(快速查找数据) Redis NoSQ…...

去除PDF论文行号的完美解决方案
去除PDF论文行号的完美解决方案 1. 遇到的问题 我想去除论文的行号,但是使用网上的Adobe Acrobat裁剪保存后 如何去掉pdf的行编号? - 知乎 (zhihu.com) 翻译时依然会出现行号,或者是转成word,这样就大大损失了格式,…...
《ElementPlus 与 ElementUI 差异集合》icon 图标使用(包含:el-button,el-input和el-dropdown 差异对比)
安装 注意 ElementPlus 的 Icon 图标 要额外安装插件 element-plus/icons-vue. npm install element-plus/icons-vue注册 全局注册 定义一个文件 element-icon.js ,注意代码第 6 行。加上了前缀 ElIcon ,避免组件命名重复,且易于理解为 e…...

力扣题库第8题:去重后的最长子串
题目: 给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: s "bbbbb" …...

CSS样式中长度单位含义解析:rpx、px、vw、vh、em、rem、pt
在 CSS 样式中,有几种常见的长度单位,包括 rpx 、 px 、 vw 和 vh 等,含义解析如下: 1 . rpx (响应像素): 是微信小程序中的一种相对长度单位,可以根据屏幕宽度进行自适应缩放。 1rp…...
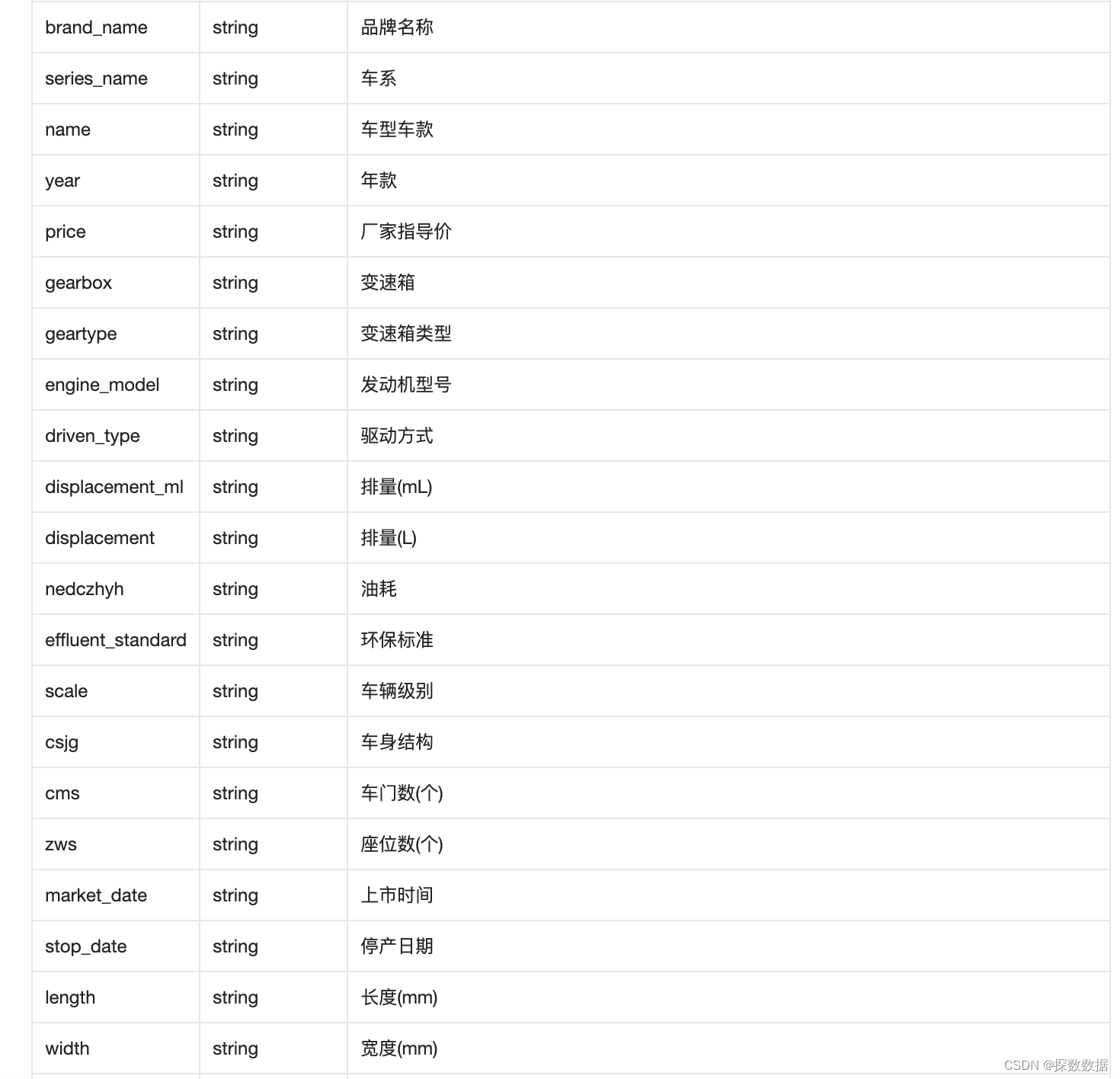
全国车辆识别代码信息API查询接口-VIN深度解析
我们先来介绍下什么是vin码,以及vin码的构成结构解析,汽车VIN码,也叫车辆识别号码,通俗可以理解为汽车的身份证号码。 VIN码一共分四大部分: 1~3位,是世界制造厂识别代号(WMI)&…...

python django 模型中字段设置blank, null属性值用法说明
问题1: ShareUser models.CharField(max_length128, blankTrue) blank设置True和false分别代表什么含义, 有什么区别?chatgpt回答的答案如下: 在 Django 模型字段中,blank 参数用于指定在创建对象时该字段是否可以为空值。它的含义如下: blankTrue:…...

暴雨信息:可持续转型更需要“以人为本”
数字化正在开启新的商业模式和价值流,为企业与组织带来巨大收益。其中,“人 (People)”这一因素至关重要。 提供更好的工作与生活体验,应对人口老龄化、劳动力短缺等挑战。对于企业而言,解决这些问题既是社会责任,也是…...
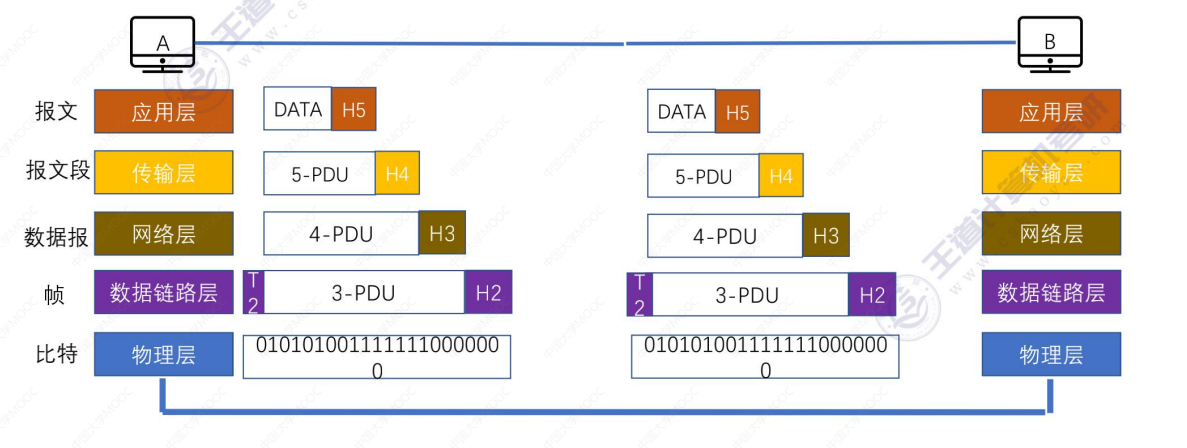
1.2_3 TCP/IP参考模型
文章目录 1.2_3 TCP/IP参考模型(一)OSI参考模型与TCP/IP参考模型(二)5层参考模型(三)5层参考模型的数据封装与解封装 1.2_3 TCP/IP参考模型 (一)OSI参考模型与TCP/IP参考模型 TCP/I…...
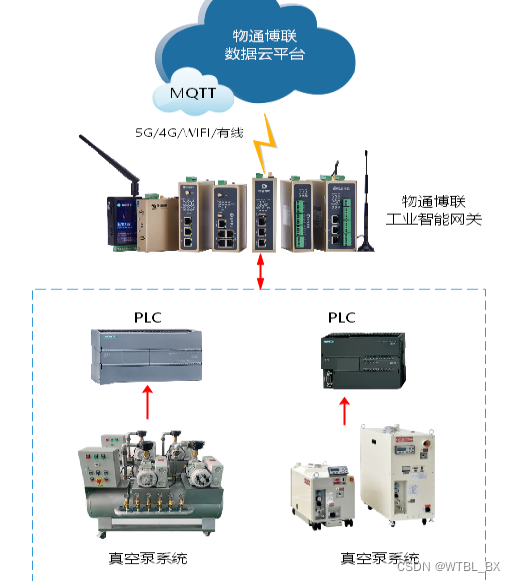
真空泵系统数据采集远程监控解决方案
行业背景 半导体制造业可以说是现代电子工业的核心产业,广泛应用于计算机、通信、汽车、医疗等领域。而在半导体生产加工过程中,如刻蚀、 镀膜、 扩散、沉积、退火等环节,真空泵都是必不可少的关键设备,它可以构建稳定受控的真空…...
Python语言在编程业界的地位——《跟老吕学Python编程》附录资料
Python语言在编程业界的地位——《跟老吕学Python编程》附录资料 ⭐️Python语言在编程业界的地位2024年3月编程语言排行榜(TIOBE前十) ⭐️Python开发语言开发环境介绍1.**IDLE**2.⭐️PyCharm3.**Anaconda**4.**Jupyter Notebook**5.**Sublime Text** …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...
