吴恩达深度学习笔记:神经网络的编程基础2.9-2.14
目录
- 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
- 第二周:神经网络的编程基础 (Basics of Neural Network programming)
- 2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
第二周:神经网络的编程基础 (Basics of Neural Network programming)
2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
本节我们讨论怎样通过计算偏导数来实现逻辑回归的梯度下降算法。它的关键点是几个重要公式,其作用是用来实现逻辑回归中梯度下降算法。但是在本节视频中,我将使用计算图对梯度下降算法进行计算。我必须要承认的是,使用计算图来计算逻辑回归的梯度下降算法有点大材小用了。但是,我认为以这个例子作为开始来讲解,可以使你更好的理解背后的思想。从而在讨论神经网络时,你可以更深刻而全面地理解神经网络。接下来让我们开始学习逻辑回归的梯度下降算法。
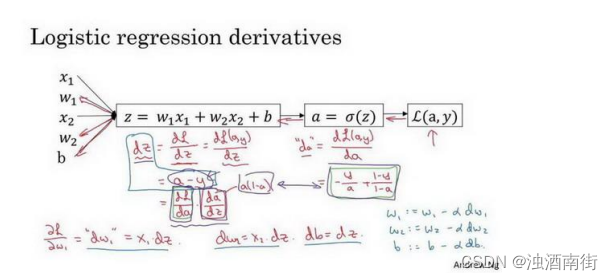
假设样本只有两个特征 x 1 x_1 x1和 x 2 x_2 x2,为了计算𝑧,我们需要输入参数 w 1 、 w 2 w_1、w_2 w1、w2 和𝑏,除此之外还有特征值 x 1 x_1 x1和 x 2 x_2 x2。因此𝑧的计算公式为: z = w 1 x 1 + w 2 x 2 + b z = w_1x_1 + w_2x_2 + b z=w1x1+w2x2+b;
回想一下逻辑回归的公式定义如下:
y ^ = a = σ ( z ) 其中 z = w T x + b , σ ( z ) = 1 1 + e − z \hat{y}= a = σ(z) 其中 z= w^Tx + b, σ(z) =\frac{1}{1+e^{-z}} y^=a=σ(z)其中z=wTx+b,σ(z)=1+e−z1
损失函数: L ( y ^ ( i ) , y ( i ) ) = − y ( i ) log ( y ^ ( i ) ) − ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) L( \hat{y}^{(i)},y^{(i)}) = -y^{(i)} \log(\hat{y}^{(i)}) - (1-y^{(i)}) \log(1-\hat{y}^{(i)}) L(y^(i),y(i))=−y(i)log(y^(i))−(1−y(i))log(1−y^(i))
代价函数: J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b) = \frac{1}{m} \sum_{i=1}^{m} L( \hat{y}^{(i)},y^{(i)}) J(w,b)=m1i=1∑mL(y^(i),y(i))
假设现在只考虑单个样本的情况,单个样本的代价函数定义如下:
L ( a , y ) = − ( y log ( a ) + ( 1 − y ) log ( 1 − a ) ) L( a,y) = -(y \log(a) + (1-y) \log(1-a)) L(a,y)=−(ylog(a)+(1−y)log(1−a))
其中𝑎是逻辑回归的输出,𝑦是样本的标签值。现在让我们画出表示这个计算的计算图。
这里先复习下梯度下降法,𝑤和𝑏的修正量可以表达如下:

如图:在这个公式的外侧画上长方形。然后计算: 𝑦^ = 𝑎 = 𝜎(𝑧) 也就是计算图的下一步。最后计算损失函数𝐿(𝑎, 𝑦)。 有了计算图,我就不需要再写出公式了。因此,为了使得逻辑回归中最小化代价函数𝐿(𝑎, 𝑦),我们需要做的仅仅是修改参数𝑤和𝑏的值。前面我们已经讲解了如何在单个训练样本上计算代价函数的前向步骤。现在让我们来讨论通过反向计算出导数。 因为我们想要计算出的代价函数𝐿(𝑎, 𝑦)的导数,首先我们需要反向计算出代价函数𝐿(𝑎, 𝑦)关于𝑎的导数,在编写代码时,你只需要用𝑑𝑎 来表示 d L ( a , y ) d a \frac{dL(a,y)}{da} dadL(a,y)。
通过微积分得到: d L ( a , y ) d a = − y a + 1 − y 1 − a \frac{dL(a,y)}{da}=\frac{-y}{a}+\frac{1-y}{1-a} dadL(a,y)=a−y+1−a1−y
如果你不熟悉微积分,也不必太担心,我们会列出本课程涉及的所有求导公式。那么如果你非常熟悉微积分,我们鼓励你主动推导前面介绍的代价函数的求导公式,使用微积分直接求出𝐿(𝑎, 𝑦)关于变量𝑎的导数。如果你不太了解微积分,也不用太担心。现在我们已经计算出𝑑𝑎,也就是最终输出结果的导数。 现在可以再反向一步,在编写 Python 代码时,你只需要用𝑑𝑧来表示代价函数𝐿关于𝑧 的导数 d L d z \frac{dL}{dz} dzdL,也可以写成 d L ( a , y ) d z \frac{dL(a,y)}{dz} dzdL(a,y),这两种写法都是正确的。 d L d z = a − y \frac{dL}{dz} = a-y dzdL=a−y。
因为 d L ( a , y ) d z = d L d z = ( d L d a ) ∗ ( d a d z ) \frac{dL(a,y)}{dz} =\frac{dL}{dz}=(\frac{dL}{da})*(\frac{da}{dz}) dzdL(a,y)=dzdL=(dadL)∗(dzda),并且 d a d z = a ∗ ( 1 − a ) \frac{da}{dz} =a*(1-a) dzda=a∗(1−a),而 d L d a = ( − y a + 1 − y 1 − a ) \frac{dL}{da}= (\frac{-y}{a}+ \frac{1-y}{1-a}) dadL=(a−y+1−a1−y),因此将这两项相乘,得到:
d z = d L ( a , y ) d z = d L d z = d L d a ∗ d a d z = ( − y a + 1 − y 1 − a ) ∗ a ( 1 − a ) = a − y dz=\frac{dL(a,y)}{dz} =\frac{dL}{dz}=\frac{dL}{da}*\frac{da}{dz}=(\frac{-y}{a}+\frac{1-y}{1-a})*a(1-a) =a-y dz=dzdL(a,y)=dzdL=dadL∗dzda=(a−y+1−a1−y)∗a(1−a)=a−y
视频中为了简化推导过程,假设𝑛𝑥这个推导的过程就是我之前提到过的链式法则。如果你对微积分熟悉,放心地去推导整个求导过程,如果不熟悉微积分,你只需要知道𝑑𝑧 = (𝑎 −𝑦)已经计算好了。
现在进行最后一步反向推导,也就是计算𝑤和𝑏变化对代价函数𝐿的影响,特别地,可以用:
d w 1 = 1 m ∑ n = i m x 1 ( i ) ( a ( i ) − y ( i ) ) dw_1=\frac{1}{m}\sum_{n=i}^mx_1^{(i)}(a^{(i)} -y^{(i)}) dw1=m1n=i∑mx1(i)(a(i)−y(i))
d w 2 = 1 m ∑ n = i m x 2 ( i ) ( a ( i ) − y ( i ) ) dw_2=\frac{1}{m}\sum_{n=i}^mx_2^{(i)}(a^{(i)} -y^{(i)}) dw2=m1n=i∑mx2(i)(a(i)−y(i))
d b = 1 m ∑ n = i m ( a ( i ) − y ( i ) ) db=\frac{1}{m}\sum_{n=i}^m(a^{(i)} -y^{(i)}) db=m1n=i∑m(a(i)−y(i))
视频中, 𝑑𝑤1 表示 ∂ L ∂ w 1 = x 1 ⋅ d z ∂L ∂w_1= x_1 ⋅ dz ∂L∂w1=x1⋅dz, 𝑑𝑤2 表示 ∂ L ∂ w 2 = x 2 ⋅ d z ∂L∂w_2= x_2 ⋅ dz ∂L∂w2=x2⋅dz, d b = d z db = dz db=dz。
因此,关于单个样本的梯度下降算法,你所需要做的就是如下的事情:
使用公式 d z = ( a − y ) dz = (a − y) dz=(a−y)计算𝑑𝑧,
使用 d w 1 = x 1 ⋅ d z dw_1 = x_1 ⋅ dz dw1=x1⋅dz 计算𝑑𝑤1, d w 2 = x 2 ⋅ d z dw_2 = x_2 ⋅ dz dw2=x2⋅dz计算𝑑𝑤2, d b = d z db= dz db=dz 来计算𝑑𝑏,
然后: 更新 w 1 = w 1 − α d w 1 w_1 = w_1 − αdw_1 w1=w1−αdw1, 更新 w 2 = w 2 − α d w 2 w_2 = w_2 − αdw_2 w2=w2−αdw2, 更新 b = b − α d b b = b − αdb b=b−αdb。
这就是关于单个样本实例的梯度下降算法中参数更新一次的步骤。
现在你已经知道了怎样计算导数,并且实现针对单个训练样本的逻辑回归的梯度下降算法。但是,训练逻辑回归模型不仅仅只有一个训练样本,而是有𝑚个训练样本的整个训练集。因此在下一节视频中,我们将这些思想应用到整个训练样本集中,而不仅仅只是单个样本上。
相关文章:

吴恩达深度学习笔记:神经网络的编程基础2.9-2.14
目录 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)第二周:神经网络的编程基础 (Basics of Neural Network programming)2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent) 第一门课ÿ…...
在C++项目中使用python脚本(四种)常见报错解决
上一期我们讲了如何在C中使用python脚本,这期讲讲过程中常会遇到的一些错误。 一、c代码未设置python路径 Py_SetPythonHome(L"D:\\anaconda3\\envs\\envpython3.7");这一句很重要,切记加上并且换成自己的路径 Py_SetPythonHome(L"D:\\a…...
微前端框架 qiankun 配置使用【基于 vue/react脚手架创建项目 】
qiankun官方文档:qiankun - qiankun 一、创建主应用: 这里以 vue 为主应用,vue版本:2.x // 全局安装vue脚手架 npm install -g vue/clivue create main-app 省略 vue 创建项目过程,若不会可以自行百度查阅教程 …...

nodejs切换淘宝源
1. 查看当前地址 npm config get registrynpm config get disturl2. 设置当前地址(设置为淘宝镜像) npm config set registry http://registry.npm.taobao.org/3. 设置当前地址(设置为默认地址) npm config set registry https…...

怎么避免电脑数据被拷贝?电脑如何禁用USB功能?
在无纸化办公的今天,很多重要数据都存放在电脑中。为了避免数据泄露,需要采用安全的方式保护电脑数据。那么,该如何避免电脑数据被拷贝呢?下面我们就来了解一下。 方法一:物理隔绝 物理隔绝是一种原始但有效的USB禁用…...
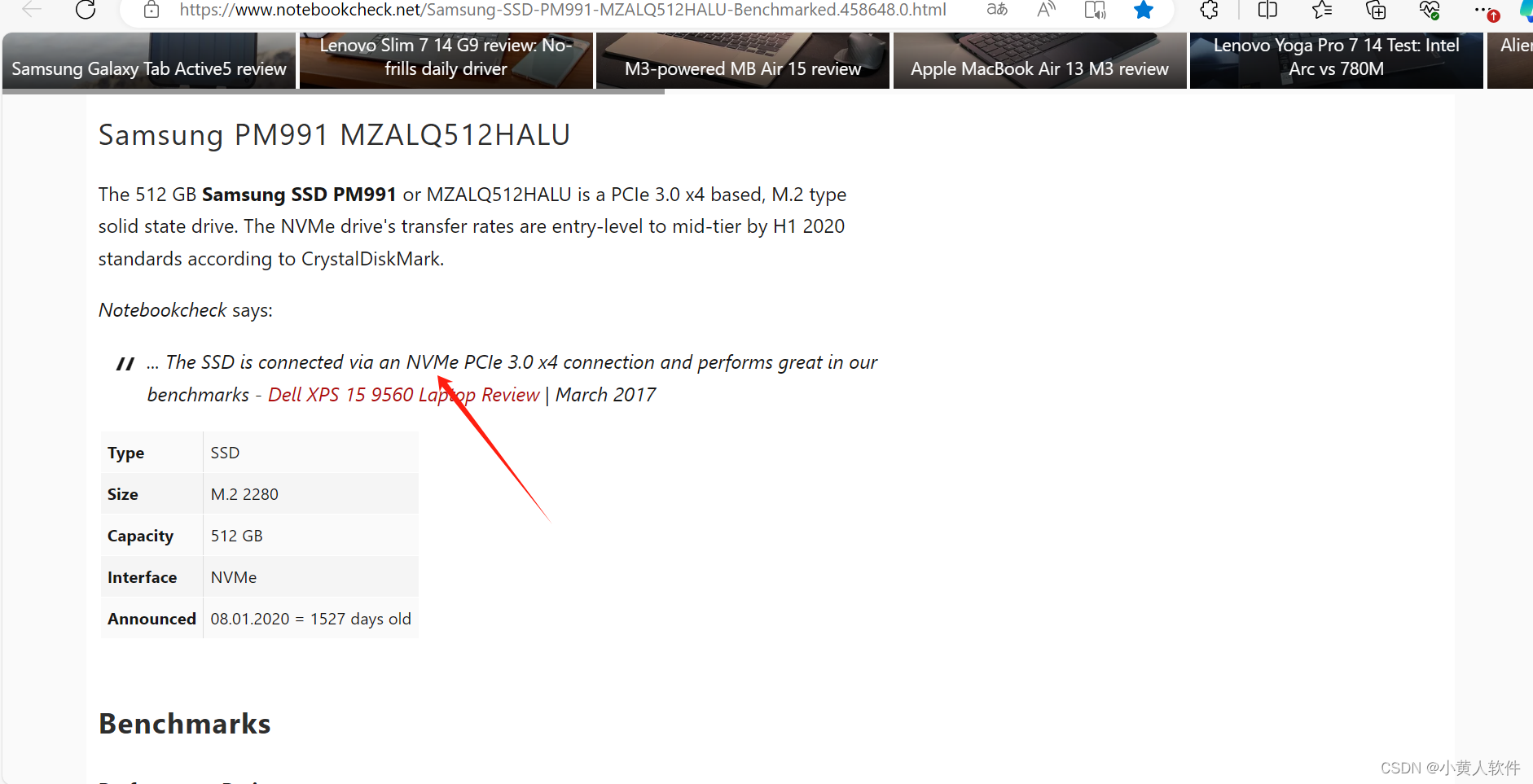
给电脑加硬件的办法 先找电脑支持的接口,再买相同接口的
需求:我硬盘太小,换或加一个大硬盘 结论:接口是NVMe PCIe 3.0 x4 1.找到硬盘型号 主硬盘 三星 MZALQ512HALU-000L2 (512 GB / 固态硬盘) 2.上官网查 或用bing查 非官方渠道信息,不确定。...

uniapp微信小程序_自定义交费逻辑编写
一、首先看最终效果 先说下整体逻辑,选中状态为淡紫色,点击哪个金额,充值页面上就显示多少金额 二、代码 <view class"addMoney"><view class"addMoneyTittle">充值金额</view><view class"selfaddmoney" :class"{…...
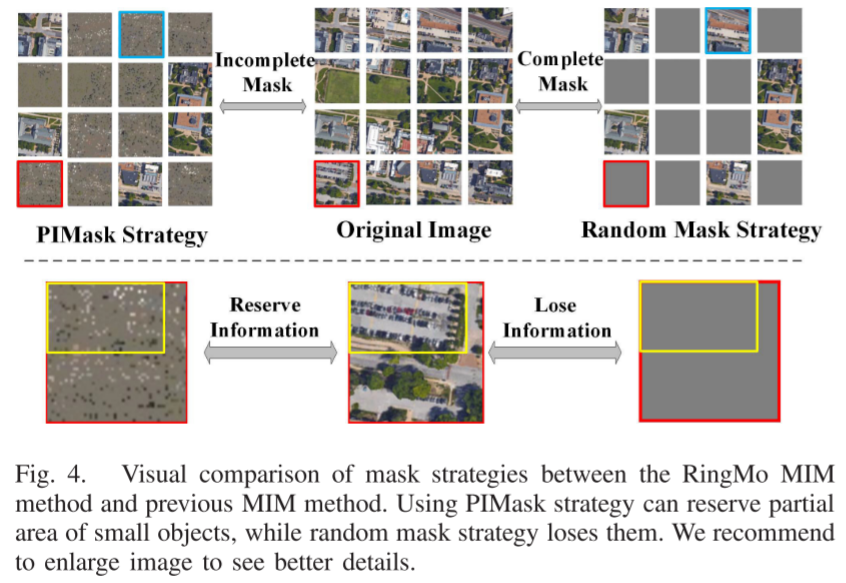
论文阅读——RingMo
RingMo: A Remote Sensing Foundation Model With Masked Image Modeling 与自然场景相比,RS图像存在以下困难。 1)分辨率和方位范围大:受遥感传感器的影响,图像具有多种空间分辨率。此外,与自然图像的实例通常由于重…...
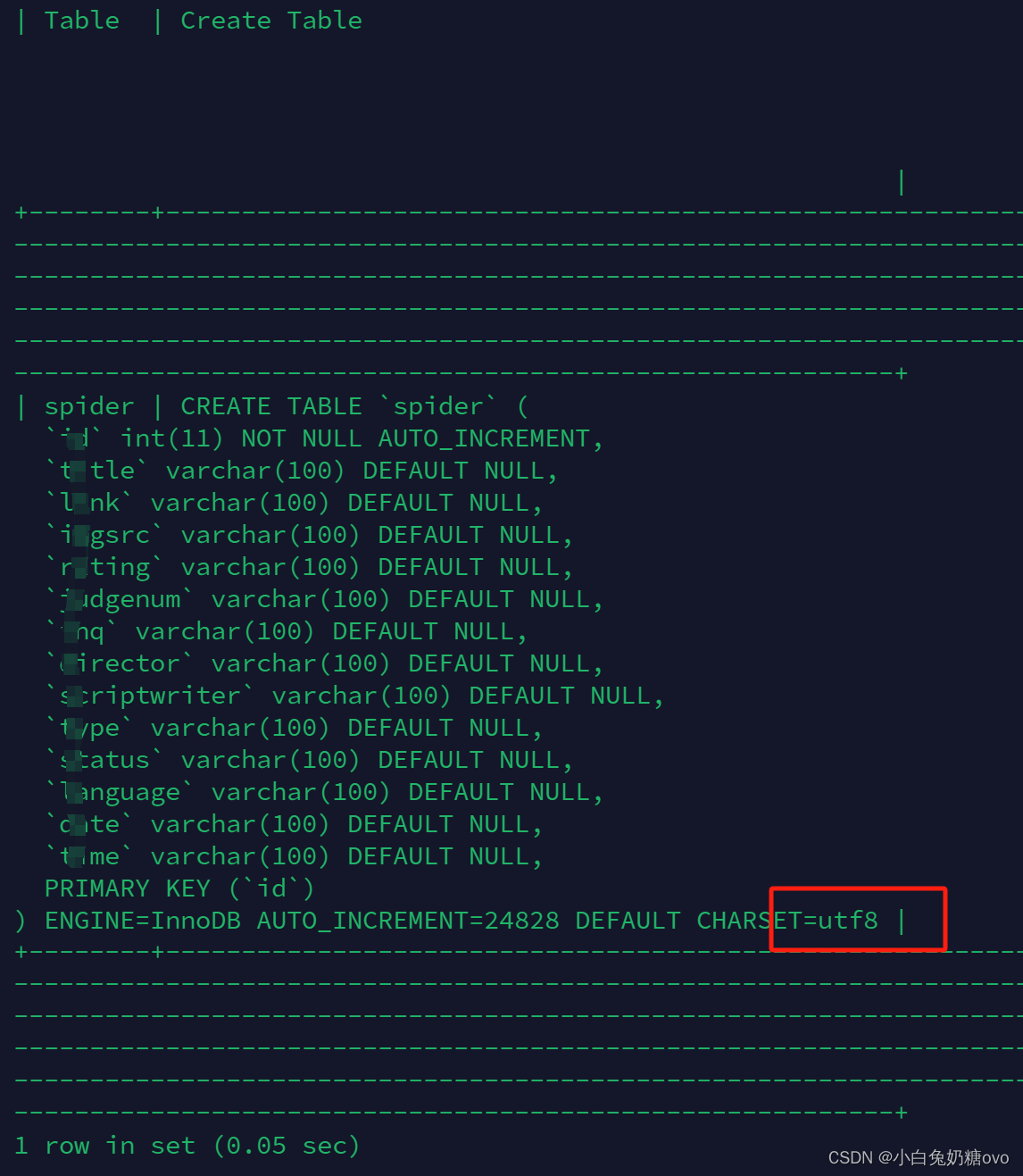
Hadoop,Hive 数据预处理CR
记录一次大材小用,我在将.csv电影数据集 电影json数据 导入MySQL时,出现了报错: 很明显,意味着.csv中的数据有非utf8编码的, 尝试使用file查看了下.csv文件的编码格式: 如果不确定原始编码,可以先用file命令尝试检测一下: file -i input.csv该命令会显示文件的MIME类型…...
)
小程序开发——获取设备信息 API(三)
ty.device.getShareDeviceInfo 获取共享设备信息 需引入DeviceKit,且在>2.2.0版本才可使用 请求参数 Object object 属性类型默认值必填说明deviceIdstring是deviceId 设备 idcompletefunction否接口调用结束的回调函数(调用成功、失败都会执行&am…...
Vue2 + node.js项目
1、Vue2 vue2主要功能包括登入、退出、用户权限、表格的增删改查、文件下载。 Vue2项目地址https://gitee.com/www6/finance1.git 2、node.js编写后端接口 2.1、项目初始化 后端地址https://gitee.com/www6/finance-backend.git 创建项目 npm install -g koa-generator …...

如何使用IDE端通义灵码
如何使用IDE端通义灵码 第一步:安装IDE插件( VS Code 和 JetBrains 二选一) 如何下载安装VS Code :https://code.visualstudio.com 如何下载安装JetBrains:https://www.jetbrains.com/idea/download 第二步&#x…...
微服务分布式springcloud的体育场地预约系统演kdm1z
体育场馆设施预约系统是在实际应用和软件工程的开发原理之上,运用java语言以及Springcloud框架进行开发。首先要进行需求分析,分析出体育场馆设施预约系统的主要功能,然后设计了系统结构。整体设计包括系统的功能、系统总体结构、系统数据结构…...

IDEA开启Run Dashboard
1、Run Dashboard是什么,为什么要使用 Run Dashboard 是 IntelliJ IDEA 中的一个工具窗口,用于管理和监视项目中正在运行的应用程序和配置。它提供了一种集中管理运行和调试过程的方式,可以让开发人员更方便地查看和控制正在运行的应用程序。…...

小程序学习3 goods-card
pages/home/home home.wxml <goods-listwr-class"goods-list-container"goodsList"{{goodsList}}"bind:click"goodListClickHandle"bind:addcart"goodListAddCartHandle"/> <goods-list>是一个自定义组件,它具…...

【投稿优惠-EI稳定检索】2024年图像处理与机械系统工程国际学术会议 (ICIPMSE 2024)
【投稿优惠-EI稳定检索】2024年图像处理与机械系统工程国际学术会议 (ICIPMSE 2024) 大会主题: (主题包括但不限于, 更多主题请咨询会务组苏老师) 图像处理 基于图像的渲染 计算机视觉 可视化分析 模式识别 3D打印 渲染和动画 渲染技术 电脑动画 基于草图的建模 机械…...
Linux系列
安装系列 1.MySQL安装 我们要通过rpm,进行MySQL数据库的安装,主要的步骤如下: rpm -qa 查询当前系统中安装的所有软件 rpm -qa | grep mysql 查询当前系统中安装的名称带mysql的软件 rpm -…...

SQL笔记 -- 黑马程序员
SQL目录 文章目录 SQL目录一、SQL分类1、DDL2、数据类型3、DML4、DQL1)基本查询2)条件查询3)聚合函数查询4)分组查询5)排序查询6)分页查询 5、DCL 一、SQL分类 分类说明DDL数据定义语言,用来定…...
C# MES通信从入门到精通(1)——串口传输文件
前言: 在上位机软件开发领域,有一些工厂的mes系统需要我们通过串口发送文件的方式把一些图片或者检测数据csv文件等发送给服务器,这种方式是一些比较旧的工厂采用的方式,但是这种方式也是存在的,本文就是讲解如何使用串口发送文件详情见下文。 1、串口发送文件思路 将需…...

论文阅读-federated unlearning via class-discriminative pruning
论文阅读-federated unlearning via class-discriminative pruning FUCP 通过类别区分性剪枝进行联邦遗忘 综述中描述:属于面向全局模型中的局部参数调整 利用卷积层的结构特定进行联邦忘却学习,wang等人提出了针对图像分类任务的联邦忘却学习算法FUCP&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
