Python和MATLAB数字信号波形和模型模拟
要点
- Python和MATLAB实现以下波形和模型模拟
- 以给定采样率模拟正弦信号,生成给定参数的方波信号,生成给定参数隔离矩形脉冲,生成并绘制线性调频信号。
- 快速傅里叶变换结果释义:复数离散傅里叶变换、频率仓和快速傅里叶变换移位,逆快速傅里叶变换移位,数值NumPy对比观察FFT移位和逆FFT移位。
- 离散时域表示:余弦信号生成取样,使用FFT频域信号表示,使用FFT计算离散傅里叶变换DFT,获得幅度谱并提取正确的相位谱,从频域样本重建时域信号。
- 功率谱密度:使用数值计算库NumPy和科学计算包SciPy以及韦尔奇功率谱密度估计方法 绘制载波调制信号的功率谱密度。
- 信号功率:生成的 10 个正弦波周期并绘图,使用数值库NumPy计算信号功率,使用科学计算包SciPy计算频域中总功率。
- 信号中多项式:SciPy计算托普利茨矩阵
- 信号卷积计算方法:暴力方法计算卷积矢量,托普利茨矩阵方法,快速傅里叶变换方法,对比不同方法计算结果。
- 使用频域方法生成分析信号,研究分析信号的组成部分,使用傅立叶变换进行希尔伯特变换:演示从实值调制信号构造的分析信号中提取瞬时幅度和相位,演示使用希尔伯特变换简单的相位解调。
- 使用二元相移键控调制传入二元流的函数,解调二元相移键控信号,使用二元相移键控调制的信息传输波形模拟生成。
- 差分编码和差分解码波形模拟生成
- 差分编码二元相移键控调制解调模拟波形
- 使用正交相移键控调制传入的二元流模拟波形,解调正交相移键控模拟波形
- 偏移正交相移键控调制解调模拟波形
- 差分编码偏移正交相移键控调制解调相位映射器和调制解调
信号处理Python示例
信号处理是一门科学领域,涉及信号从时域到频域的处理,反之亦然,平滑信号,从信号中分离噪声,即过滤,从信号中提取信息。自然界中存在的信号都是连续信号。连续时间(或模拟)信号存在于连续间隔 ( t 1 , t 2 ) (\mathrm{t} 1, \mathrm{t} 2) (t1,t2) 范围从 − ∞ -\infty −∞ 到 + ∞ +\infty +∞。
模拟量转数字量
- 采样:采样是将连续时间信号还原为离散时间信号。一个常见的例子是将声波(连续信号)转换为样本序列(离散时间信号)
- 量化:量化是将输入值从大集合(通常是连续集合)映射到(可数)较小集合(通常具有有限数量的元素)中的输出值的过程。 路由和截断是量化过程的典型示例。
- 编码:对每个样本进行量化并确定每个样本的位数后,可以将每个样本变为nb位码字。每个样本的位数由量化级别的数量确定。
import numpy as np
import matplotlib.pyplot as pltimport scipy
from scipy import signal
t = np.arange(0, 11)
x = (0.85) ** t
连续信号
plt.figure(figsize = (10,8)) # set the size of figure# 1. Plotting Analog Signal
plt.subplot(2, 2, 1)
plt.title('Analog Signal', fontsize=20)plt.plot(t, x, linewidth=3, label='x(t) = (0.85)^t')
plt.xlabel('t' , fontsize=15)
plt.ylabel('amplitude', fontsize=15)
plt.legend(loc='upper right')# 2. Sampling and Plotting of Sampled signal
plt.subplot(2, 2, 2)
plt.title('Sampling', fontsize=20)
plt.plot(t, x, linewidth=3, label='x(t) = (0.85)^t')
n = tmarkerline, stemlines, baseline = plt.stem(n, x, label='x(n) = (0.85)^n')
plt.setp(stemlines, 'linewidth', 3)
plt.xlabel('n' , fontsize = 15)
plt.ylabel('amplitude', fontsize = 15)
plt.legend(loc='upper right')# 3. Quantization
plt.subplot(2, 2, 3)
plt.title('Quantization', fontsize = 20)plt.plot(t, x, linewidth =3)
markerline, stemlines, baseline=plt.stem(n,x)
plt.setp(stemlines, 'linewidth', 3)
plt.xlabel('n', fontsize = 15)
plt.ylabel('Range of Quantizer', fontsize=15)plt.axhline(y = 0.1, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.2, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.3, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.4, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.5, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.6, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.7, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.8, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.9, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 1.0, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)plt.subplot(2, 2, 4)
plt.title('Quantized Signal', fontsize = 20)
xq = np.around(x,1)
markerline, stemlines, baseline = plt.stem(n,xq)
plt.setp(stemlines, 'linewidth', 3)
plt.xlabel('n', fontsize = 15)
plt.ylabel('Range of Quantizer', fontsize=15)plt.axhline(y = 0.1, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.2, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.3, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.4, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.5, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.6, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.7, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.8, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 0.9, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)
plt.axhline(y = 1.0, xmin = 0, xmax = 10, color = 'r', linewidth = 3.0)plt.tight_layout()单位脉冲信号
impulse = signal.unit_impulse(10, 'mid')
shifted_impulse = signal.unit_impulse(7, 2)# Sine wave
t = np.linspace(0, 10, 100)
amp = 5 # Amplitude
f = 50
x = amp * np.sin(2 * np.pi * f * t)# Exponential Signal
x_ = amp * np.exp(-t)
plt.figure(figsize=(10, 8))plt.subplot(2, 2, 1)
plt.plot(np.arange(-5, 5), impulse, linewidth=3, label='Unit impulse function')
plt.ylim(-0.01,1)
plt.xlabel('time.', fontsize=15)
plt.ylabel('Amplitude', fontsize=15)
plt.legend(fontsize=10, loc='upper right')plt.subplot(2, 2, 2)
plt.plot(shifted_impulse, linewidth=3, label='Shifted Unit impulse function')plt.xlabel('time.', fontsize=15)
plt.ylabel('Amplitude', fontsize=15)
plt.legend(fontsize=10, loc='upper right')plt.subplot(2, 2, 3)
plt.plot(t, x, linewidth=3, label='Sine wave')plt.xlabel('time.', fontsize=15)
plt.ylabel('Amplitude', fontsize=15)
plt.legend(fontsize=10, loc='upper right')plt.subplot(2, 2, 4)
plt.plot(t, x_, linewidth=3, label='Exponential Signal')plt.xlabel('time.', fontsize=15)
plt.ylabel('Amplitude', fontsize=15)
plt.legend(fontsize=10, loc='upper right')plt.tight_layout()
正弦波
# Sine wave
n = np.linspace(0, 10, 100)
amp = 5 # Amplitude
f = 50
x = amp * np.sin(2 * np.pi * f * n)# Exponential Signal
x_ = amp * np.exp(-n)
离散信号
plt.figure(figsize=(12, 8))plt.subplot(2, 2, 1)
plt.stem(n, x, 'yo', label='Sine wave')plt.xlabel('time.', fontsize=15)
plt.ylabel('Amplitude', fontsize=15)
plt.legend(fontsize=10, loc='upper right')plt.subplot(2, 2, 2)
plt.stem(n, x_, 'yo', label='Exponential Signal')plt.xlabel('time.', fontsize=15)
plt.ylabel('Amplitude', fontsize=15)
plt.legend(fontsize=10, loc='upper right')
傅里叶变换
傅里叶变换是分析信号的强大工具,可用于从音频处理到图像处理再到图像压缩的各个领域。傅里叶分析是研究如何将数学函数分解为一系列更简单的三角函数的领域。 傅立叶变换是该领域的一种工具,用于将函数分解为其分量频率。 换句话说,傅立叶变换是一种工具,可让您获取信号并查看其中每个频率的功率。 看看这句话中的重要术语:
- 信号是随时间变化的信息。例如,音频、视频和电压迹线都是信号的示例。
- 频率是某事物重复的速度。例如,时钟以一赫特 (Hz) 的频率滴答,或每秒重复一次。
- 在这种情况下,功率仅指每个频率的强度。
下图是一些正弦波的频率和功率的直观演示:
高频正弦波的峰值比低频正弦波的峰值更接近,因为它们重复得更频繁。低功率正弦波的峰值比其他两个正弦波小。
傅立叶变换在许多应用中都很有用。 图像压缩使用傅立叶变换的变体来去除图像的高频分量。 语音识别使用傅里叶变换和相关变换从原始音频中恢复口语单词。
一般来说,如果您需要查看信号中的频率,则需要傅立叶变换。如果在时域处理信号很困难,那么使用傅立叶变换将其移至频域值得尝试。
参阅一:计算思维
参阅二:亚图跨际
相关文章:

Python和MATLAB数字信号波形和模型模拟
要点 Python和MATLAB实现以下波形和模型模拟 以给定采样率模拟正弦信号,生成给定参数的方波信号,生成给定参数隔离矩形脉冲,生成并绘制线性调频信号。快速傅里叶变换结果释义:复数离散傅里叶变换、频率仓和快速傅里叶变换移位&am…...
华为OD技术C卷“测试用例执行计划”Java解答
描述 示例 算法思路1 整体思路是,先读取特性的优先级和测试用例覆盖的特性列表,然后计算每个测试用例的优先级,并将其与测试用例的索引存储到二维数组中。最后按照优先级和索引排序,输出测试用例的索引,即为执行顺序。…...

solana 入门 1
solana-co-learn Solana 开发学习笔记(一)——从 Hello World 出发 安装开发环境 windows下环境配置 wsl First start with installing WSL on your system. wsl --install wsl安装Ubuntu 列出可用的分发版 wsl.exe --list --online显示: 以下是可安装的有效…...
JavaEE之多线程(创建线程的五种写法)详解
😽博主CSDN主页: 小源_😽 🖋️个人专栏: JavaEE 😀努力追逐大佬们的步伐~ 目录 1. 前言 2. 操作系统"内核" 3. 创建线程的五种写法 (我们重点要掌握最后一种写法!!) 3.1 继承 Thread, 重写 run 3. 2 实现 Runnabl…...

ChatGPT国内能用吗?中国用户怎么才能使用ChatGPT?
与ChatGPT类似的国内网站,他们都能提供和ChatGPT相似的能力,而且可以在国内直接使用。 点击直达方式 百科GPT官网:baikegpt.cn ChatGPT是基于GPT-3.5架构的语言模型的一个实例,由OpenAI开发。以下是ChatGPT的发展历史࿱…...

集群保持集群负载均衡和hash一致性
集群保持负载均衡和一致性哈希是在构建分布式系统时经常涉及的两个重要概念。 负载均衡: - 在集群中,负载均衡是指将传入的请求有效地分发到不同的服务器上,以确保每台服务器都能够处理适量的流量,避免某些服务器过载而造成性能问…...
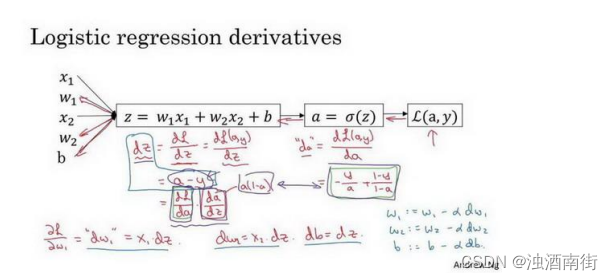
吴恩达深度学习笔记:神经网络的编程基础2.9-2.14
目录 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)第二周:神经网络的编程基础 (Basics of Neural Network programming)2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent) 第一门课ÿ…...
在C++项目中使用python脚本(四种)常见报错解决
上一期我们讲了如何在C中使用python脚本,这期讲讲过程中常会遇到的一些错误。 一、c代码未设置python路径 Py_SetPythonHome(L"D:\\anaconda3\\envs\\envpython3.7");这一句很重要,切记加上并且换成自己的路径 Py_SetPythonHome(L"D:\\a…...
微前端框架 qiankun 配置使用【基于 vue/react脚手架创建项目 】
qiankun官方文档:qiankun - qiankun 一、创建主应用: 这里以 vue 为主应用,vue版本:2.x // 全局安装vue脚手架 npm install -g vue/clivue create main-app 省略 vue 创建项目过程,若不会可以自行百度查阅教程 …...

nodejs切换淘宝源
1. 查看当前地址 npm config get registrynpm config get disturl2. 设置当前地址(设置为淘宝镜像) npm config set registry http://registry.npm.taobao.org/3. 设置当前地址(设置为默认地址) npm config set registry https…...

怎么避免电脑数据被拷贝?电脑如何禁用USB功能?
在无纸化办公的今天,很多重要数据都存放在电脑中。为了避免数据泄露,需要采用安全的方式保护电脑数据。那么,该如何避免电脑数据被拷贝呢?下面我们就来了解一下。 方法一:物理隔绝 物理隔绝是一种原始但有效的USB禁用…...
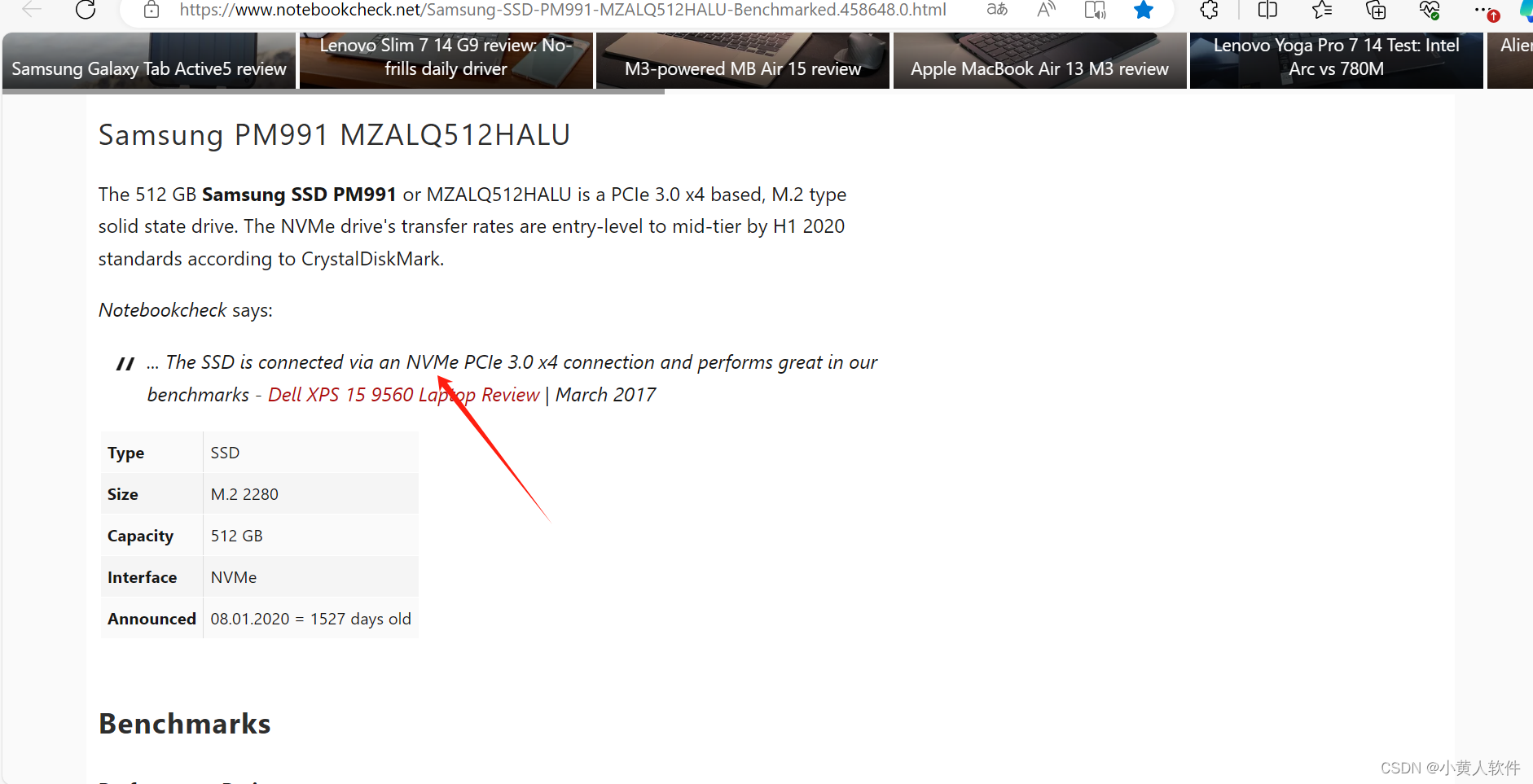
给电脑加硬件的办法 先找电脑支持的接口,再买相同接口的
需求:我硬盘太小,换或加一个大硬盘 结论:接口是NVMe PCIe 3.0 x4 1.找到硬盘型号 主硬盘 三星 MZALQ512HALU-000L2 (512 GB / 固态硬盘) 2.上官网查 或用bing查 非官方渠道信息,不确定。...

uniapp微信小程序_自定义交费逻辑编写
一、首先看最终效果 先说下整体逻辑,选中状态为淡紫色,点击哪个金额,充值页面上就显示多少金额 二、代码 <view class"addMoney"><view class"addMoneyTittle">充值金额</view><view class"selfaddmoney" :class"{…...
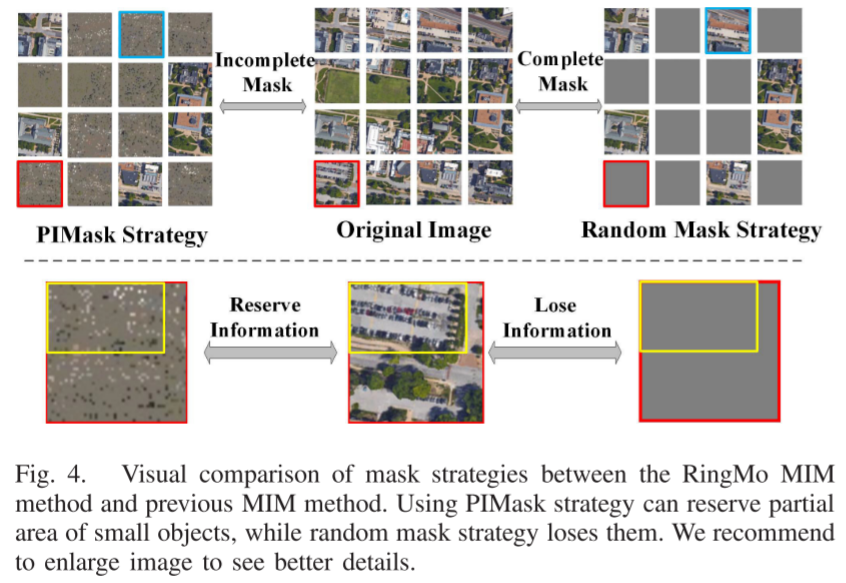
论文阅读——RingMo
RingMo: A Remote Sensing Foundation Model With Masked Image Modeling 与自然场景相比,RS图像存在以下困难。 1)分辨率和方位范围大:受遥感传感器的影响,图像具有多种空间分辨率。此外,与自然图像的实例通常由于重…...
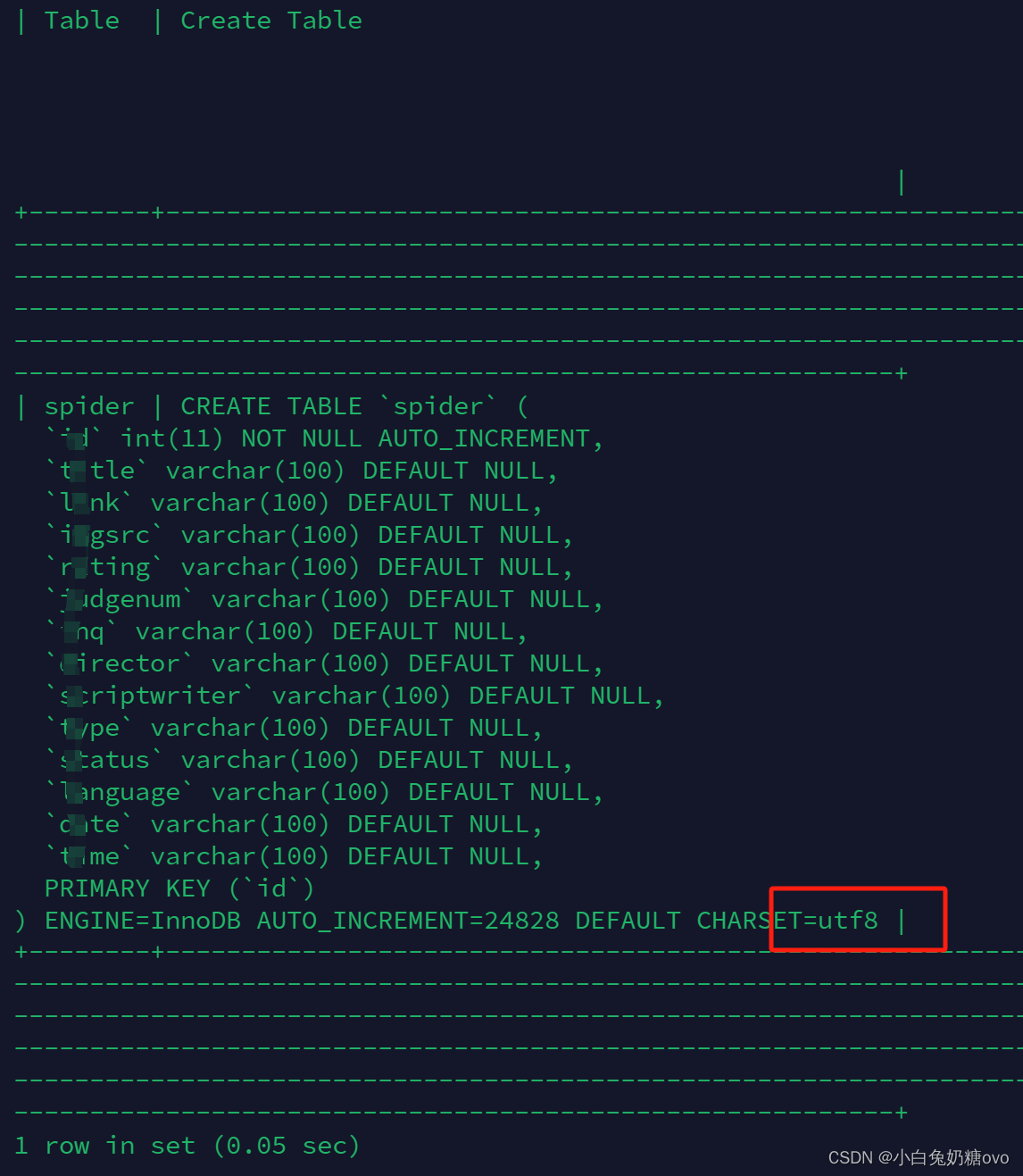
Hadoop,Hive 数据预处理CR
记录一次大材小用,我在将.csv电影数据集 电影json数据 导入MySQL时,出现了报错: 很明显,意味着.csv中的数据有非utf8编码的, 尝试使用file查看了下.csv文件的编码格式: 如果不确定原始编码,可以先用file命令尝试检测一下: file -i input.csv该命令会显示文件的MIME类型…...
)
小程序开发——获取设备信息 API(三)
ty.device.getShareDeviceInfo 获取共享设备信息 需引入DeviceKit,且在>2.2.0版本才可使用 请求参数 Object object 属性类型默认值必填说明deviceIdstring是deviceId 设备 idcompletefunction否接口调用结束的回调函数(调用成功、失败都会执行&am…...
Vue2 + node.js项目
1、Vue2 vue2主要功能包括登入、退出、用户权限、表格的增删改查、文件下载。 Vue2项目地址https://gitee.com/www6/finance1.git 2、node.js编写后端接口 2.1、项目初始化 后端地址https://gitee.com/www6/finance-backend.git 创建项目 npm install -g koa-generator …...

如何使用IDE端通义灵码
如何使用IDE端通义灵码 第一步:安装IDE插件( VS Code 和 JetBrains 二选一) 如何下载安装VS Code :https://code.visualstudio.com 如何下载安装JetBrains:https://www.jetbrains.com/idea/download 第二步&#x…...
微服务分布式springcloud的体育场地预约系统演kdm1z
体育场馆设施预约系统是在实际应用和软件工程的开发原理之上,运用java语言以及Springcloud框架进行开发。首先要进行需求分析,分析出体育场馆设施预约系统的主要功能,然后设计了系统结构。整体设计包括系统的功能、系统总体结构、系统数据结构…...

IDEA开启Run Dashboard
1、Run Dashboard是什么,为什么要使用 Run Dashboard 是 IntelliJ IDEA 中的一个工具窗口,用于管理和监视项目中正在运行的应用程序和配置。它提供了一种集中管理运行和调试过程的方式,可以让开发人员更方便地查看和控制正在运行的应用程序。…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
