【算法与数据结构】深入解析二叉树(一)

文章目录
- 📝数概念及结构
- 🌠 树的概念
- 🌉树的表示
- 🌠 树在实际中的运用(表示文件系统的目录树结构)
- 🌉二叉树概念及结构
- 🌠概念
- 🌉数据结构中的二叉树
- 🌠特殊的二叉树:
- 🌉 二叉树的性质
- 🌠二叉树的存储结构
- 🌉 顺序存储
- 🌠链式存储
- 🌉 选择题
- 🚩总结
📝数概念及结构
🌠 树的概念
数是一种非线性的数据结构,它是由n(n>=0)个有限节点组成一个具有层次关系的集合,把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
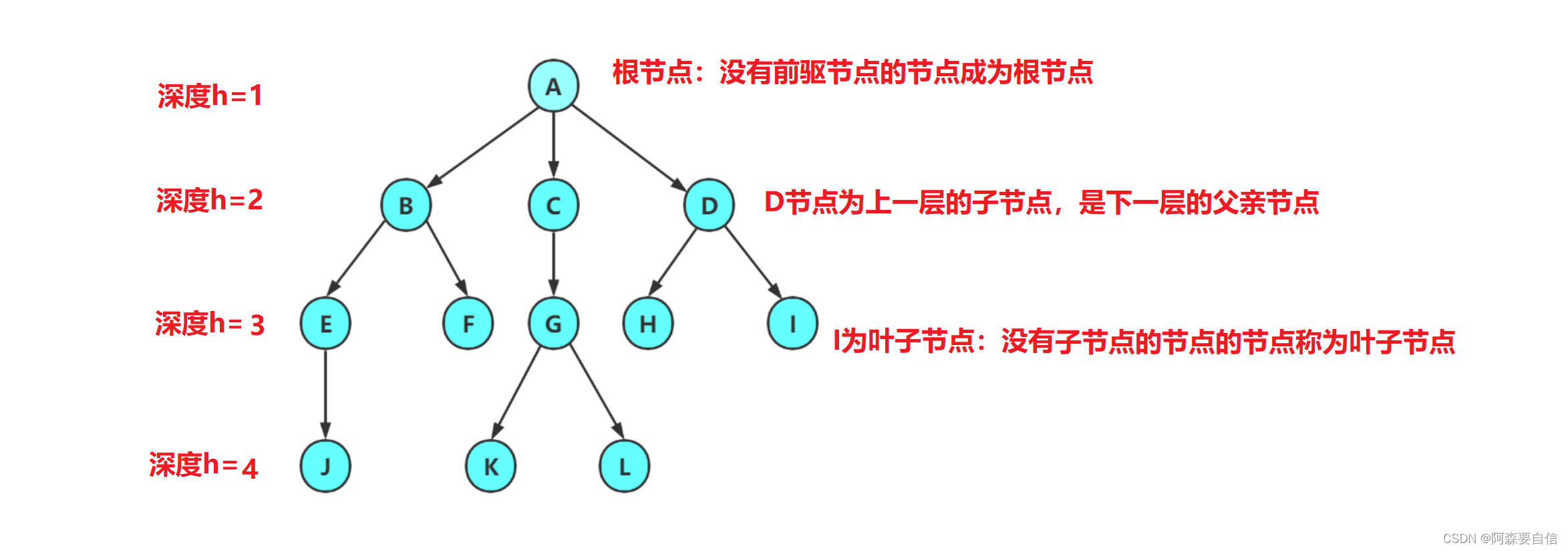
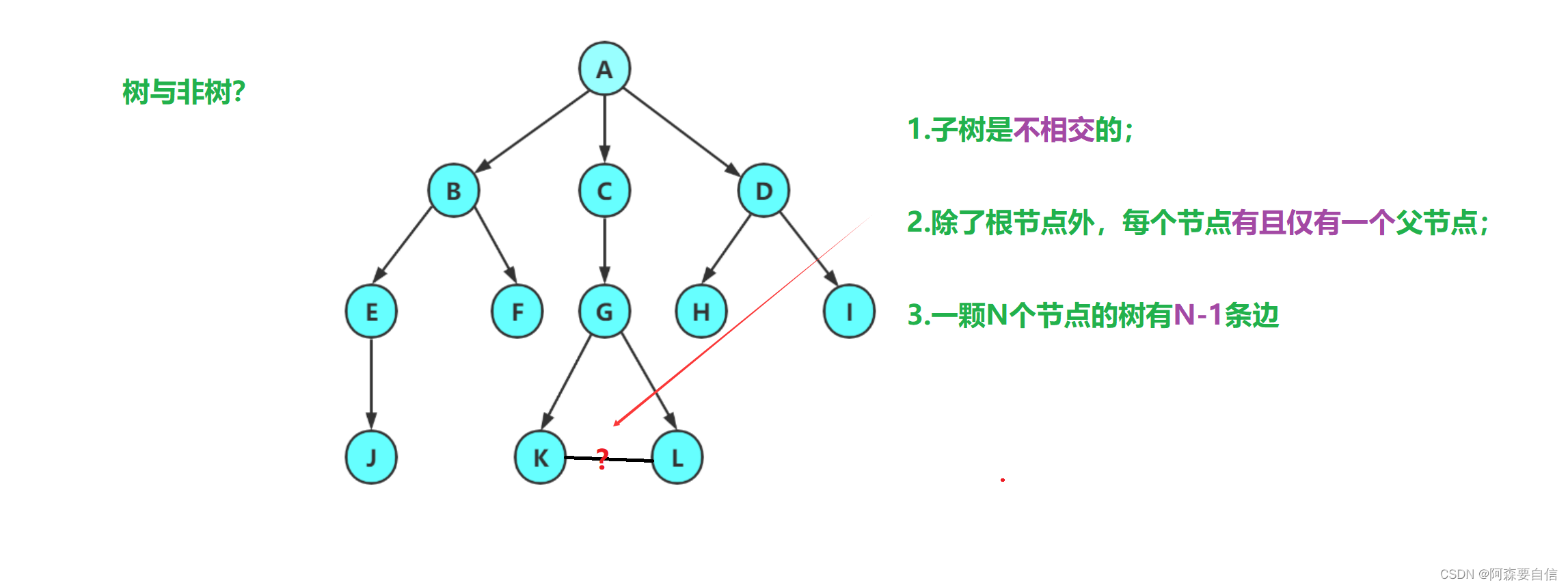
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
树的相关概念
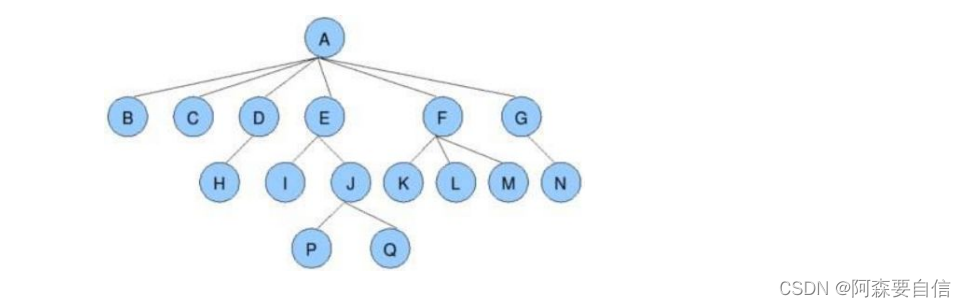
- 节点的度:一个节点含有子树的个数称为该节点的度;如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I…等节点为叶节点
- 非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G…等节点为分支节点
- 双亲节点或父节点:若一个节点包含子节点,则这个节点称其字节点的父节点;如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点互为兄弟节点;如图:B,C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
🌉树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
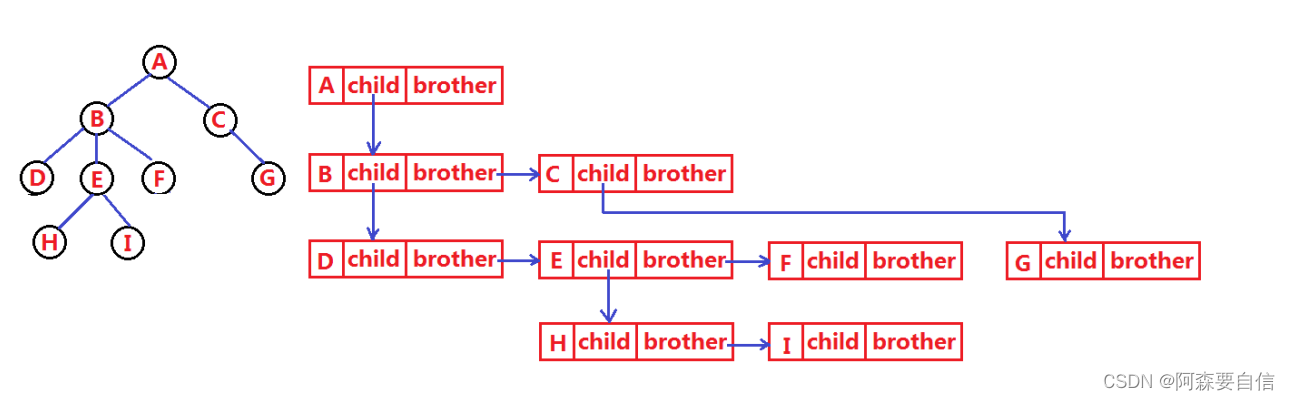
🌠 树在实际中的运用(表示文件系统的目录树结构)
Linux文件系统中也广泛使用树状图来表示和管理目录结构:Linux文件系统中的目录结构就是一棵树,根目录位于树的顶部,使用命令如tree、find等可以生成目录的树状图,清晰展示各目录和文件的包含关系。VFS(虚拟文件系统)层次结构也采用树形结构,不同文件系统作为树的分支,方便管理和扩展。
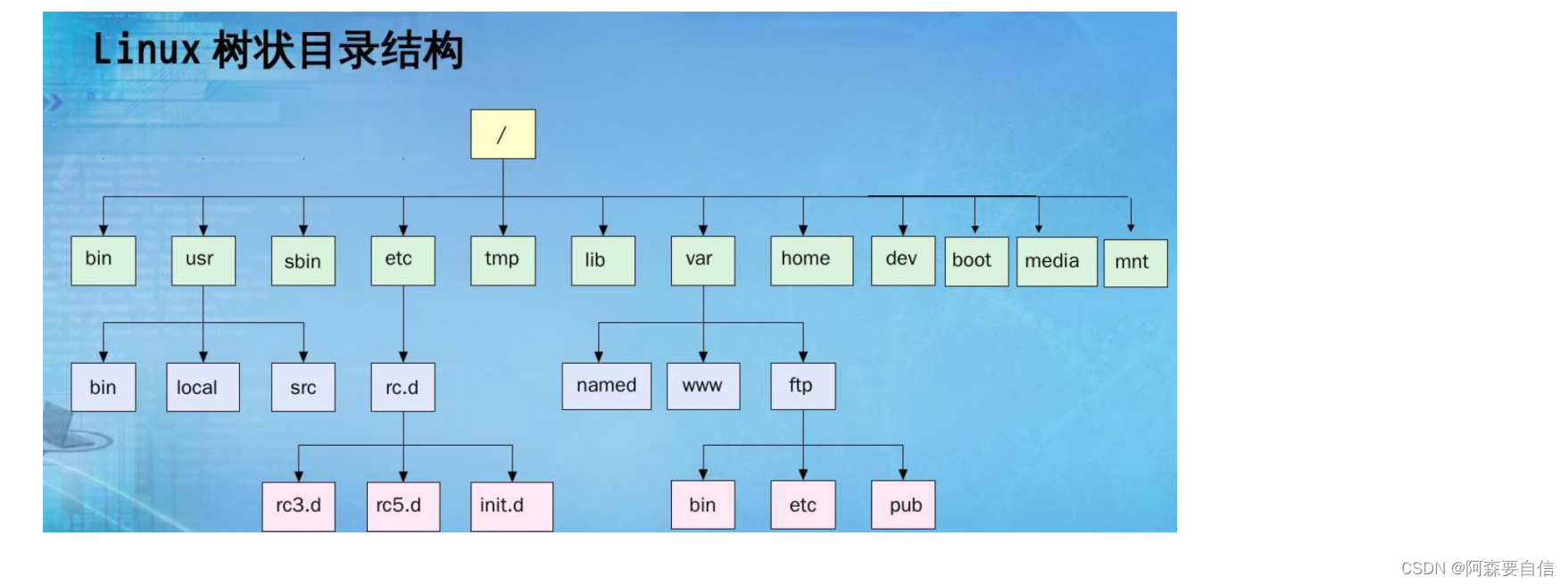
🌉二叉树概念及结构
🌠概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
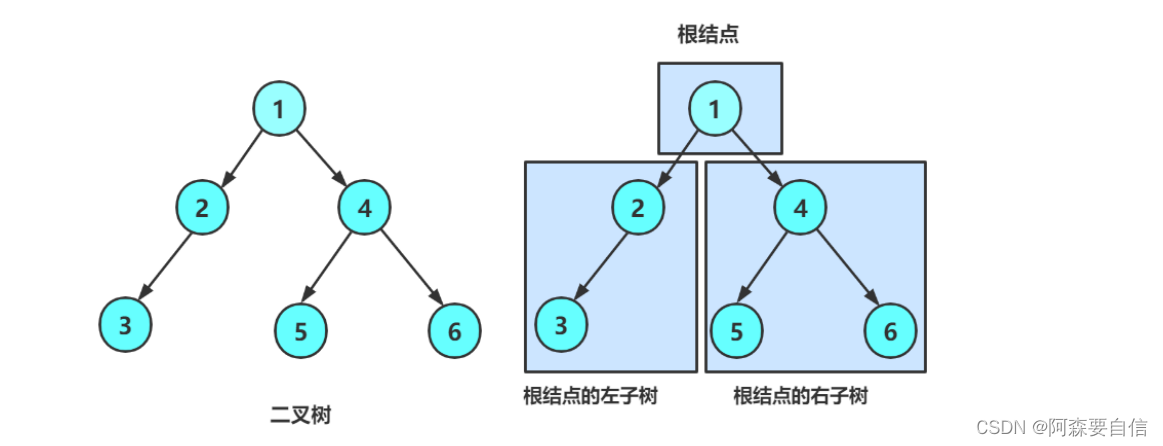
二叉树的特点: - 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
🌉数据结构中的二叉树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
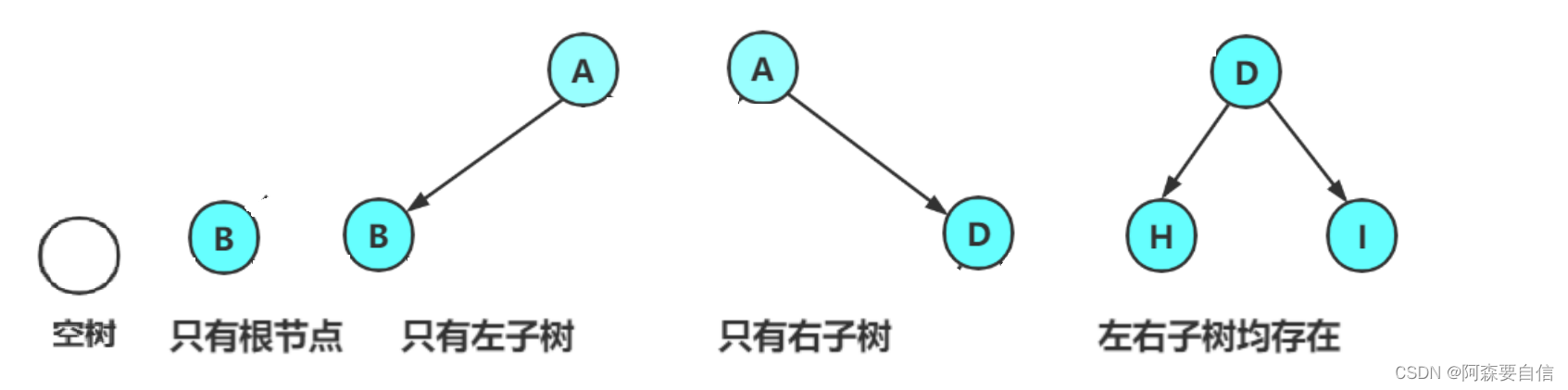
🌠特殊的二叉树:
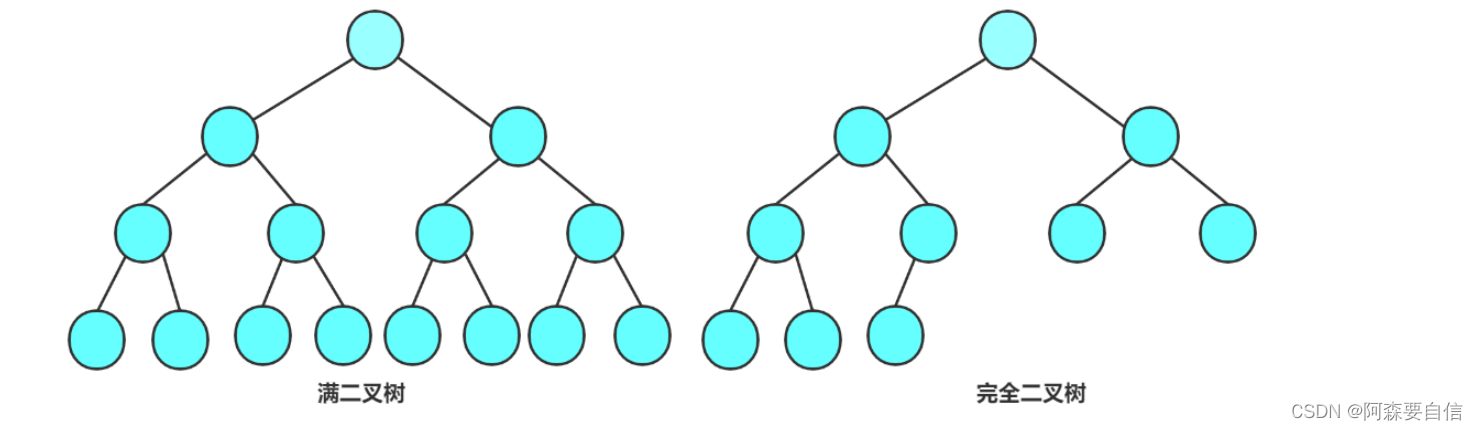
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
🌉 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是是 2^h-1(注意是这里是-1+2 ^h)
- 对任何一棵二叉树来说,如果:N0是度为0(叶结点)的节点个数N2是度为2(分支结点)的节点个数则有:N0 + N2 = N - 1(N0(叶节点个数) + N2(分支节点个数) = 总节点数N)
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log_2(n+1) = h (ps: 是log以2为底,n+1为对数)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
🌠二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
🌉 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
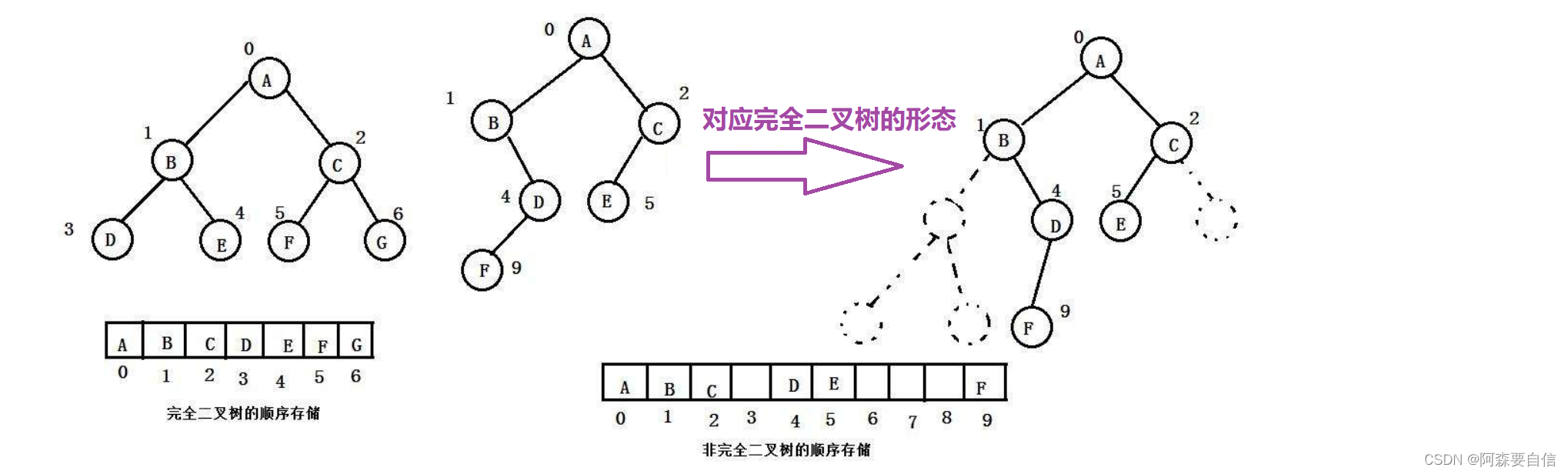
🌠链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
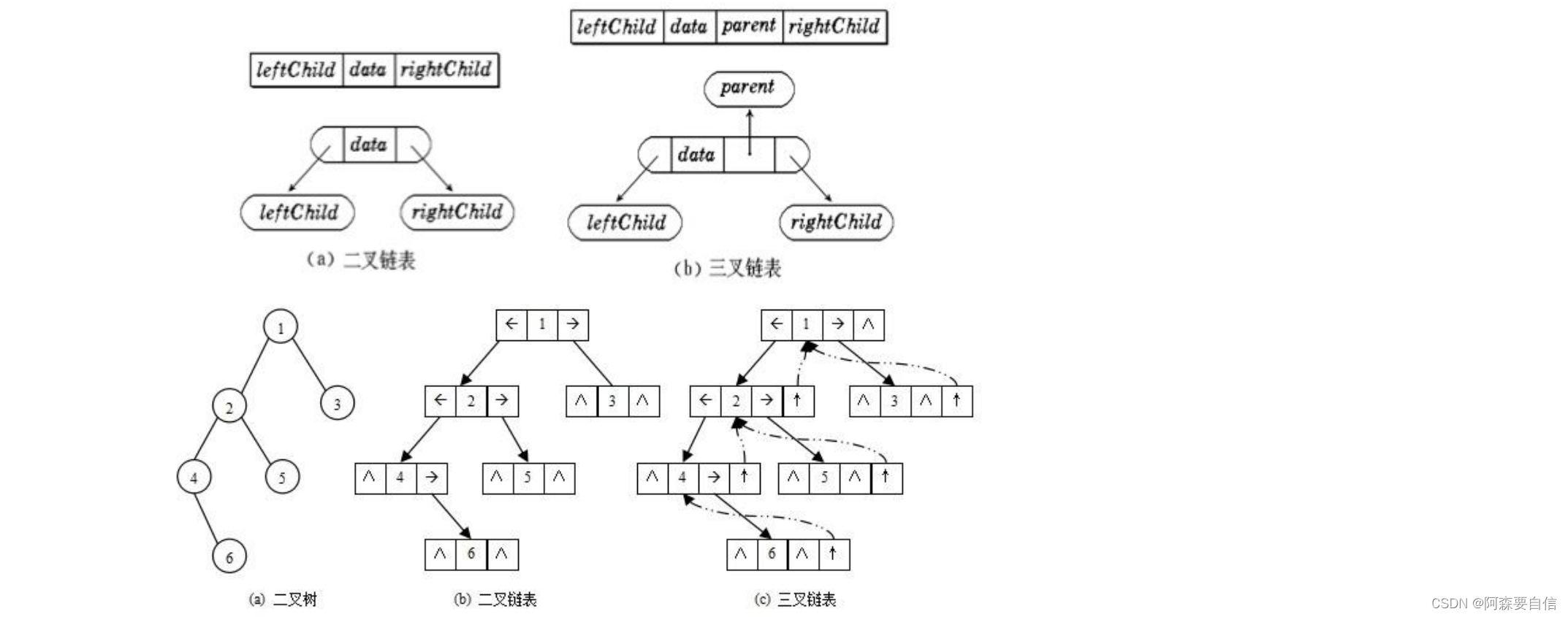
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
🌉 选择题
来趁热练铁吧,冲冲冲~
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
解题思路:
总结点数为399个,度为2的结点数为199个,每个度为2的结点都有2个儿子,那么199个度为2的结点对应的子结点数为199*2=398,总结点数399,度为2结点对应的子结点数398,则叶子结点数为399-398=1
正确答案是B 200
2.下列数据结构中,不适合采用顺序存储结构的是( )
A 非完全二叉树
B 堆
C 队列
D 栈
顺序存储结构是指数据元素按顺序依次存储在连续的内存单元中。A 非完全二叉树:非完全二叉树采用顺序存储,会有很多空闲位置,存储效率不高。
正确答案是A
3.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
完全二叉树的定义: 如果设二叉树深度为h,除最后一层外,其他各层节点数达到最大个数,最后一层所有结点从左到右排列,这就是完全二叉树。对于一个具有2n个结点的完全二叉树:除最后一层外,其他各层节点数都达到最大个数,即都是满的。最后一层可能不满,但结点从左到右排列。一个满二叉树的节点数为2h-1,这里树的深度h,使得2h-1<=2n<2h+1,即h=log2(2n)=log2n,除最后一层外共有log2n层,每层节点数为2h-1,共有log2n*(2h-1)=n个节点
最后一层节点数即为叶子节点数,为2n-n=n个
正确答案是A
🚩总结

相关文章:

【算法与数据结构】深入解析二叉树(一)
文章目录 📝数概念及结构🌠 树的概念🌉树的表示🌠 树在实际中的运用(表示文件系统的目录树结构) 🌉二叉树概念及结构🌠概念🌉数据结构中的二叉树🌠特殊的二叉…...

深入浅出:Objective-C中使用MWFeedParser下载豆瓣RSS
摘要 本文旨在介绍如何在Objective-C中使用MWFeedParser库下载豆瓣RSS内容,同时展示如何通过爬虫代理IP技术和多线程提高爬虫的效率和安全性。 背景 随着信息量的激增,爬虫技术成为了获取和处理大量网络数据的重要手段。Objective-C作为一种成熟的编程…...

Java日志框架Log4j 2详解
有时希望能够以文件的形式记录执行过程中出现的异常信息,甚至记录程序正常运行的关键步骤,以便日后查看,那么该如何处理呢? 答:显然,可以自行编程实现这个需求,但是,从更注重效率和性能的方面考虑&#x…...
【剪枝实战】使用VGGNet训练、稀疏训练、剪枝、微调等,剪枝出只有3M的模型
摘要 本次剪枝实战是基于下面这篇论文去复现的,主要是实现对BN层的γ/gamma进行剪枝操作,本文用到的代码和数据集都可以在我的资源中免费下载到。 相关论文:Learning Efficient Convolutional Networks through Network Slimming (ICCV 2017…...
OSI(Open Systems Interconnection)模型和TCP/IP模型
OSI模型 OSI模型是一个概念模型,由国际标准化组织(ISO)在1984年提出,用于促进不同系统间的通信互联。OSI模型将网络通信的过程分为七层,每一层都有其特定的功能,从下至上依次是: 物理层&#x…...
)
git基础命令(二)
目录 git revert 撤消上一次提交的更改但是会创建一个新的提交来撤消该提交所做的更改git show 显示提交详细信息git mv 重命名文件git rm 从工作树和索引中移除文件git clean 从工作树中移除未跟踪文件git checkout 将文件恢复到工作树git reset 撤销更改、移动 HEAD 指针以及…...
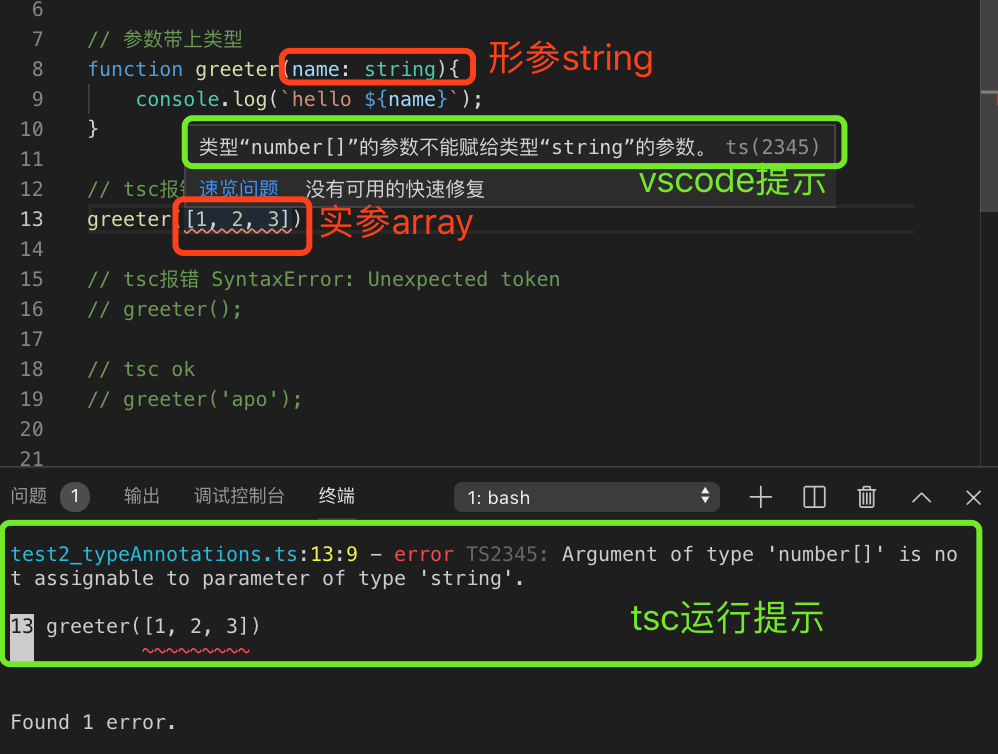
从零开始学习typescript系列 1:typescript 基本了解之是什么,为什么,以及怎么用
初识ts 基本了解 设计者,实现者:微软发行时间:2012年10月1日GitHub:https://github.com/microsoft/TypeScriptts和js关系:ts是js的扩展,ts语法包含js ts是新语言吗? 不是,在js基…...

【数学建模】线性规划
针对未来可能的数学建模比赛内容,我对学习的内容做了一些调整,所以先跳过灰色关联分析和模糊综合评价的代码,今天先来了解一下运筹规划类——线性规划模型。 背景: 某数学建模游戏有三种题型,分别是A,B&am…...

MQTT 的 QoS 等级:QoS 0、QoS 1、QoS 2
MQTT(Message Queuing Telemetry Transport)是一种轻量级的通信协议,在物联网和消息传递系统中广泛应用。MQTT 提供了三个不同的 QoS(Quality of Service)等级,用于确保消息的可靠性和传输效率。本文将详细…...

搭建个人智能家居 3 -第一个设备“点灯”
搭建个人智能家居 3 -第一个外设“点灯” 前言ESPHome点灯 HomeAssistant 前言 前面我们已经完成了搭建这个智能家居所需要的环境HomeAssistant和ESPHome,今天我们开始在这个智能家居中添加我们的第一个设备(一颗LED灯),如果环境…...

基于 RocketMQ Prometheus Exporter 打造定制化 DevOps 平台
tar -xzf prometheus-2.7.0-rc.1.linux-amd64.tar.gzcd prometheus-2.7.0-rc.1.linux-amd64/./prometheus --config.fileprometheus.yml --web.listen-address:5555 Prometheus 默认监听端口号为 9090,为了不与系统上的其它进程监听端口冲突,我们在启动…...
 Object Pascal 学习笔记---第7章第1节(创建对象 ))
(delphi11最新学习资料) Object Pascal 学习笔记---第7章第1节(创建对象 )
7.1.4 创建对象 与其他流行的编程语言比较之后,让我们回到 Pascal,看看如何使用类。 一旦定义了类,我们就可以创建一个该类型的对象,代码片段如下(本节所有代码提取自 Dates1 示例)那样:…...

unity学习笔记 Restsharp 使用心得
Restsharp Restsharp安装使用注意事项api方式的流式调用--子线程中执行代码无响应的问题问题描述问题解决其他问题 Restsharp 安装 可以在github上下载dll文件然后导入到unity中 https://github.com/adrenak/RestSharp.Unity 也可以百度直接搜Restsharp然后下载相关的文件导入…...
YOLOV5 部署:QT的可视化界面推理(创建UI,并编译成py文件)
1、前言 之前用YOLOV5 做了一个猫和老鼠的实战检测项目,本章将根据之前训练好的权重进行部署,搭建一个基于QT的可视化推理界面,可以检测图片和视频 本章使用的数据集和权重参照:YOLOV5 初体验:简单猫和老鼠数据集模型训练-CSDN博客 可视化界面如下: 2、安装Pyside6 本…...

Python:自动化处理PDF文档集合,提取文献标题、合并文献PDF并生成目录和页码
Python:自动化处理PDF文档集合,提取文献标题、合并文献PDF并生成目录和页码 引言:功能概述步骤一:提取PDF标题步骤二:生成目录和页码,合并PDF技术亮点 代码步骤一:提取PDF标题(Step_…...

vue 基于elementUI/antd-vue, h函数实现message中嵌套链接跳转到指定路由 (h函数点击事件的写法)
效果如图: 点击message 组件中的 工单管理, 跳转到工单管理页面。 以下是基于vue3 antd-vue 代码如下: import { message } from ant-design-vue; import { h, reactive, ref, watch } from vue; import { useRouter } from vue-router; c…...

数字排列 - 华为OD统一考试(C卷)
OD统一考试(C卷) 分值: 200分 题解: Java / Python / C 题目描述 小明负责公司年会,想出一个趣味游戏: 屏幕给出 1−9 中任意 4 个不重复的数字,大家以最快时间给出这几个数字可拼成的数字从小到大排列位于第 n 位置…...
yocto 编译raspberrypi 4B并启动
yocto 编译raspberrypi 4B并启动 环境准备 最近到手一个树莓派4B,准备拿来玩一玩,下面记录下使用yocto构建RaspberryPi的镜像并刷写启动的过程。 首先准备主机编译环境,必要组件安装: sudo apt install gawk wget git diffstat…...

Nginx、LVS、HAProxy工作原理和负载均衡架构
当前大多数的互联网系统都使用了服务器集群技术,集群是将相同服务部署在多台服务器上构成一个集群整体对外提供服务,这些集群可以是 Web 应用服务器集群,也可以是数据库服务器集群,还可以是分布式缓存服务器集群等等。 在实际应用…...

C语言标准库函数qsort( )——数据排序
大家好!我是保护小周ღ,本期为大家带来的是深度解剖C语言标准库函数 qsort(),qsort()函数他可以对任意类型的数据排序,博主会详细解释函数使用方法,以及使用快速排序的左右指针法模拟实现函数功能,这样的排…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
