matlab 基操~
MATLAB基本操作
1. 对象定义 使用sym定义单个对象、使用syms定义多个对象
2. 使用limit求极限
$$ \lim_{v \rightarrow a} f(x) $$
limit(f,v,a) % 使用limit(f,v,a,'left')可求左极限3. 导数 使用diff(f,v,n)对$ f(v)=v^{t-1} $求 $ n $ 阶导 $ \frac{d^nf}{d^nv} $,n缺省时,默认为1,diff(f)默认求一阶导数。
4. 定积分和不定积分 使用int(f,v)求f对变量v的不定积分,使用int(f,v,a,b)求f对变量v的定积分,a、b为积分上下标。$ \int{f(v)dv} $、$ \int^{a}_{b}{f(v)dv} $。
5. matlab函数文件定义形式
function [输出形参列表] = 函数名(输入形参列表)函数体function spir_len = spirallength(d, n, lcolor)
% SPIRALLENGTH plot a circle of radius as r in the provided color and calculate its area
% 输入参数:
% d: 螺旋的旋距
% n: 螺旋的圈数
% lcolor:画图线的颜色
% 输出参数:
% spir_len:螺旋的周长
% 调用说明:
% spirallength(d,n):以参数d,n画螺旋线,螺旋线默认为蓝色
% spirallength(d,n,lcolor):以参数d,n,lcolor画螺旋线
% spir_len = spirallength(d,n):计算螺旋线的周长,并以蓝色填充螺旋线
% spir_len = spirallength(d,n,lcolor):计算螺旋线的周长,并以lcolor颜色填充螺旋线% 版本号V1.0,编写于1999年9月9号,修改于1999年9月10号,作者:亚索if nargin > 3error('输入变量过多!');
elseif nargin == 2lcolor = 'b'; % 默认情况下为蓝色
endj = sqrt(-1);
phi = 0 : pi/1000 : n*2*pi;
amp = 0 : d/2000 : n*d;
spir = amp .* exp(j*phi);if nargout == 1spir_len = sum(abs(diff(spir)));fill(real(spir), imag(spir), lcolor);
elseif nargout == 0plot(spir, lcolor);
elseerror('输出变量过多!');
endaxis('square');6. matlab程序设计语句
% for循环
for 循环变量=初值:步长:终值循环体
end% while循环
while 条件循环体
end% if语句
if 条件语句组1
elseif语句组2
else语句组3
end% switch语句
switch 表达式case 表达式1语句组1case 表达式2语句组2... ...case 表达式m语句组motherwise语句组
end% try语句
try语句组1 %语句组1若正确则跳出该结构
catch语句组2
end7. 矩阵操作
| 操作 | 作用 |
|---|---|
| size(A) | 求矩阵A的行数和列数 |
| length(x) | 返回向量x的长度 |
| A' | A的转置 |
| A(:,n) | 取矩阵A第n列数,A(n,:)取第n行 |
| det(A) | 求矩阵A的行列式 |
| inv(A) | 求A的逆 |
| rank(A) | 求A的秩 |
| trace(A) | 求A的迹 |
| max(A)、min(A) | 求A的各列最大、最小元素 |
| mean(A) | 求A各列的平均值 |
| sum(A) | 求A各列元素之和 |
8. matlab简单绘图
plot函数是MATLAB中最核心的二维绘图函数,有诸多语法格式,可实现多种功能。常用格式有:
- plot(x):缺省自变量的绘图格式,x可为向量或矩阵。
- plot(x, y):基本格式,x和y可为向量或矩阵。
- plot(x1, y1, x2, y2,…):多条曲线绘图格式,在同一坐标系中绘制多个图形。
- plot(x, y,‘s’):开关格式,开关量字符串s设定了图形曲线的颜色、线型及标示符号(见下表)。
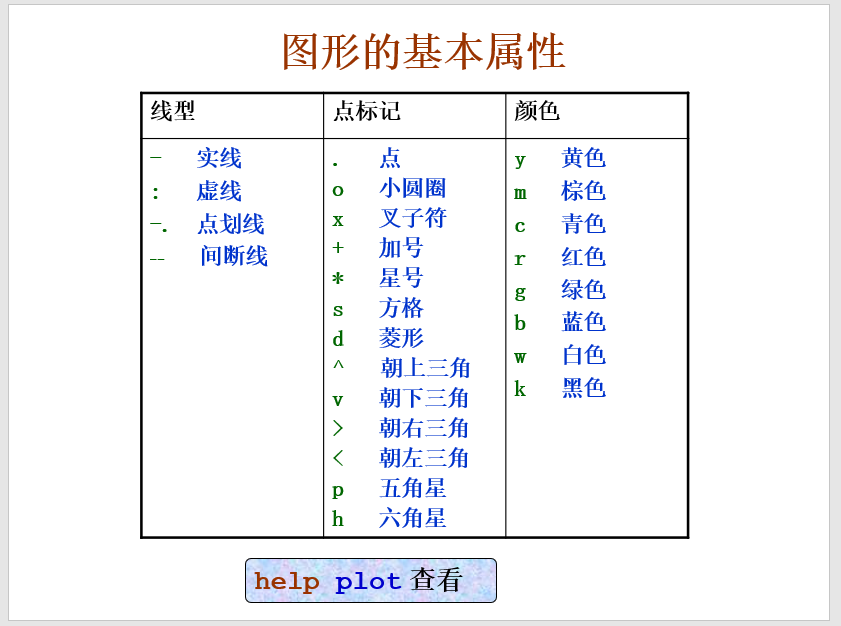
无约束优化问题求解
fminbnd、fminunc函数输出变量解释
| 变量 | 描述 |
|---|---|
| x | 由优化函数求得的值. 若exitflag>0,则x为解; 否则,x不是最终解, 它只是迭代制止时优化过程的值 |
| fval | 解 x 处的目标函数值 |
| exitflag | 描述退出条件:exitflag>0,表目标函数收敛于解x处;exitflag=0,表已达到函数评价或迭代的最大次数;exitflag<0,表目标函数不收敛 |
| output | 包含优化结果信息的输出结构。Iterations:迭代次数;Algorithm:所采用的算法;FuncCount:函数评价次数 |
一元函数无约束优化问题-fminbnd
常用格式
$$ min f(x), x_1<x<x_2 $$
(1)x= fminbnd (fun, x1, x2) (2)x= fminbnd (fun, x1, x2 , options) (3)[x , fval]= fminbnd(...) (4)[x , fval , exitflag]= fminbnd(...) (5)[x , fval , exitflag , output]= fminbnd(...) 函数fminbnd的算法基于黄金分割法和二次插值法,它要求目标函数必须是连续函数,并可能只给出局部最优解
例子
求函数 $ f(x)=2e^{-x}sin(x) $ 在 $ 0<x<8 $ 时的最小值
% 如果求最大需要对f取反
f = @(x) (2*exp(-x)*sin(x));
[x,fval] = fminbnd(f,0,8);
x
fval多元函数无约束优化问题-fminunc
常用格式
$$ min f(X),这里X为n维变量 $$ fminunc常用格式为: (1)x= fminunc(fun, X0); (2)x= fminunc(fun, X0,options); (3)[x,fval]= fminunc(...); (4)[x,fval,exitflag]= fminunc(...); (5)[x,fval,exitflag,output]= fminunc(...) 其中 X0为初始值
例子
求函数$ f(x_1,x_2)=(4x_1^2+2x_2^2+4x_1x_2+2x_2^2+1)e^x $的最小值,$ X_0=[-1,1] $
f = @(x) (4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1)*exp(x(1));
x0 = [-1,1];
[x,fval] = fminunc(f, x0);
x
fval线性规划问题求解
使用linprog求解一般线性规划问题
常见问题(linprog默认求最小值) $$ minz=cX $$
$$ s.t. \begin{cases} AX\leq{b}\ Aeq\cdot{X}=beq\ VLB\leq{X}\leq{VUB} \end{cases}$$
求解命令
[x,fval] = linprog(c,A,b,Aeq,beq,VLB,VUB)例子
$$ min z=13x_1+9x_2+10x_3+11x_4+12x_5+8x_6 $$
$$ s.t.\left{ \begin{aligned} & x_1+x_2=400\ & x_2+x_5=600\ & x_3+x_6=500\ & 0.4x_1+1.1x_2+x_3\leq{800}\ & 0.5x_4+1.2x_5+1.3x_6\leq{900}\ & x_i\geq0,i=1,2,...,6 \end{aligned} \right. $$
f = [13 9 10 11 12 8];
A = [0.4 1.1 1 0 0 00 0 0 0.5 1.2 1.3];
b = [800; 900];
Aeq=[1 0 0 1 0 00 1 0 0 1 00 0 1 0 0 1];
beq=[400 600 500];
vlb = zeros(6,1);
vub=[];
[x,fval] = linprog(f,A,b,Aeq,beq,vlb,vub)使用bintprog求解0-1规划问题
matlab2014以上版本使用intlinprog求解0-1规划问题
$$ minz=cX $$
$$ s.t. \begin{cases} AX\leq{b}\ Aeq\cdot{X}=beq\ X为0-1变量 \end{cases}$$
% 命令
[x,fval] = bintprog(c,A,b,Aeq,beq)例子
$$ min z=3x_1+7x_2-x_3+x_4 $$ $$ s.t. \begin{cases} 2x_1-x_2+x_3-x_4\geq{1}\ x_1-x_2+6x_3+4x_4\geq{8}\ 5x_1+3x_2+x_4\geq{5}\ x_i=0或1(i=1,2,3,4) \end{cases} $$
z = [3;7;-1;1];
A = [-2 1 -1 1;-1 1 -6 -4;-5 -3 0 -1];
b = [-1;-8;-5];
Aeq = [];
beq = [];[x,fval] = bintprog(z,A,b,Aeq,beq)数据插值与拟合
数据插值,使用interpl进行一维插值
matlab命令
yi = interpl(X,Y,xi,method)该命令用指定的算法找出一个一元函数,然后以该函数给出xi处的值。其中x=[x1,x2,…,xn]’和 y=[y1,y2,…,yn]’两个向量分别为给定的一组自变量和函数值,用来表示已知样本点数据;xi为待求插值点处横坐标,可以是一个标量,也可以是一个向量,是向量时,必须单调;yi得到返回的对应纵坐标。
- method可以选取以下方法之一:
- ‘nearest’:最近邻点插值,直接完成计算;
- ‘spline’:三次样条函数插值;
- ‘linear’:线性插值(缺省方式),直接完成计算;
- ‘cubic’:三次函数插值;
例子
作函数$ y=(x^2-3x+7)e^{-4x}sin(2x) $在[0,1]取间隔为0.1的点图,用插值进行实验
x=0:0.1:1;
y=(x.^2-3*x+7).*exp(-4*x).*sin(2*x); %产生原始数据subplot(1,2,1);
plot(x,y,x,y,'ro') %作图
xx=0:0.02:1; %待求插值点
yy=interp1(x,y,xx,'spline'); %此处可用nearest,cubic,spline分别试验subplot(1,2,2)
plot(x,y,'ro',xx,yy,'b') %作图曲线拟合
拟合函数polyfit
p=polyfit(x,y,n)
[p,s]= polyfit(x,y,n)说明:x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。p是n+1维参数向量p(1),p(2)….那么拟合后对应的多项式即为: $$ p(1)x^n+p(2)x^{n-1}+\cdot\cdot\cdot+p(n)x+p(n+1) $$
x必须是单调的。矩阵s用于生成预测值的误差估计
多项式求值函数polyval
y=polyval(p,x)
[y,DELTA]=polyval(p,x,s)说明:y=polyval(p,x)为返回对应自变量x在给定系数p的多项式的值; [y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计DELTA。它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。则DELTA将至少包含50%的预测值。
例子
求如下给定数据的拟合曲线 x=[0.5,1.0,1.5,2.0,2.5,3.0],y=[1.75,2.45,3.81,4.80,7.00,8.60]
x=[0.5,1.0,1.5,2.0,2.5,3.0];
y=[1.75,2.45,3.81,4.80,7.00,8.60];
plot(x,y,‘*r’) %先观察数据点的大致形态
p=polyfit(x,y,2) %用二次多项式拟合
x1=0.5:0.05:3.0; % 步长0.05
y1=polyval(p,x1);
plot(x,y,'*r',x1,y1,'-b')本文由博客群发一文多发等运营工具平台 OpenWrite 发布
相关文章:

matlab 基操~
MATLAB基本操作 1. 对象定义 使用sym定义单个对象、使用syms定义多个对象 2. 使用limit求极限 $$ \lim_{v \rightarrow a} f(x) $$ limit(f,v,a) % 使用limit(f,v,a,left)可求左极限 3. 导数 使用diff(f,v,n)对$ f(v)v^{t-1} $求 $ n $ 阶导 $ \frac{d^nf}{d^nv} $…...
)
HTML5、CSS3面试题(一)
1、H5 的新特性有哪些?C3 的新特性有哪些?(必会) H5 新特性 1、拖拽释放(Drap and drop) API ondrop 拖放是一种常见的特性,即抓取对象以后拖到另一个位置 在 HTML5 中,拖放是标准的一部分,任…...

图片压缩神器源码系统:无损画质 带完整的代码安装包以及搭建教程
在数字化时代,图片已经成为我们日常生活和工作中不可或缺的一部分。然而,随着图片数量的增加和质量的提升,存储空间的问题也日益凸显。如何在保证图片质量的前提下,有效减少图片的大小,成为了一个亟待解决的问题。罗峰…...

探索SOCKS5代理、代理IP、HTTP与网络安全
在这个数字化时代,网络安全已成为我们日常生活中不可或缺的一部分。作为一名软件工程师,深入理解网络通信的核心技术,如SOCKS5代理、代理IP、HTTP协议,以及它们在网络安全中的应用,对于设计和实施安全的网络应用至关重…...

【Python学习篇】Python基础入门学习——你好Python(一)
个人名片: 🦁作者简介:学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由…...

【通信原理笔记】【二】随机信号分析——2.2 平稳随机过程
文章目录 前言一、平稳随机过程1.1 广义平稳过程1.2 遍历性 二、两个随机过程之间的关系2.1 联合平稳2.2 随机过程的相关关系2.2.1 随机变量的不相关2.2.2 随机过程的不相关 总结 前言 我们学习了随机信号以及随机信号的相关函数与功率谱的计算方法,但是这种计算还…...
新火种AI|GPT-4诞生1年,OpenAI把它放到了机器人上
作者:一号 编辑:美美 ChatGPT拥有了身体,机器人也有了灵魂。 从OpenAI在去年3月14日拿出GPT-4后,已经过了整整一年。显然,在GPT-4诞生之后的这一年,一切都迭代得太快了,从GPT-4展现多模态能力&…...
8-图像放大
其实,就是开辟一个zoomwidth,zoomheight的内存,再分别赋值即可。 void CDib::Maginify(float xZoom, float yZoom) { //指向原图像指针 LPBYTE p_data GetData(); //指向原像素的指针 LPBYTE lpSrc; //指向缩放图像对应像素的指针 LPBYTE l…...
下载,java打包压缩文件夹下载)
java实现压缩文件夹(层级压缩)下载,java打包压缩文件夹下载
工具类如下 打包下载方法:exportZip(支持整个文件夹或单文件一起) 注意:前端发送请求不能用ajax,form表单提交可以,location.href也可以,window.open也可以,总之就ajax请求就是不行 import com.…...

Visual Studio 2022 配置“Debug|x64”的 Designtime 生成失败。IntelliSense 可能不可用。
今天写代码,无缘无故就给我整个这个错误出来,我一头雾水。 经过我几个小时的奋战,终于解决问题 原因就是这个Q_INTERFACES()宏,我本想使用Q_DECLARE_INTERFACE Q_INTERFACES这两个Qt宏实现不继承QObject也能使用qobjec…...

Pandas教程16:DataFrame列标题批量重命名+空df数据判断+列名顺序重排
---------------pandas数据分析集合--------------- Python教程71:学习Pandas中一维数组Series Python教程74:Pandas中DataFrame数据创建方法及缺失值与重复值处理 Pandas数据化分析,DataFrame行列索引数据的选取,增加,…...

React.FC介绍
React.FC是React中的一种函数组件类型,是在TypeScript中使用的一个泛型,FC即Function Component的缩写,表示一个接收props作为输入并返回JSX元素的函数组件。 使用React.FC可以为组件定义类型,提供props的类型作为泛型参数&#x…...
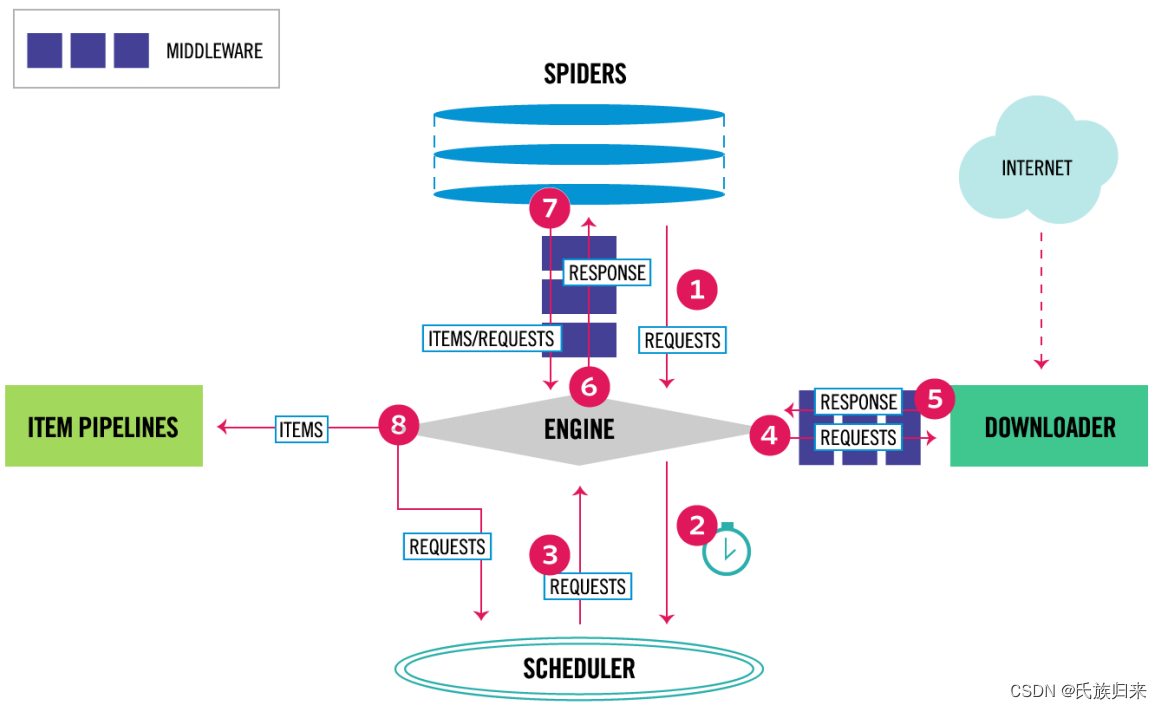
为什么要用scrapy爬虫库?而不是纯python进行爬虫?
为什么要用scrapy爬虫库?而不是纯python进行爬虫? Scrapy的优点Scrapy节省的工作使用纯Python编写爬虫的不足 Scrapy是一个使用Python编写的开源和协作的web爬虫框架,它被设计用于爬取网页数据并从中提取结构化数据。Scrapy的强大之处在于其广…...

C:数据结构王道
初始化顺序表(顺序表中元素为整型),里边的元素是1,2,3,然后通过scanf读取一个元素(假如插入的是6),插入到第2个位置,打印输出顺序表,每个元素占3个空格,格式为…...
Compose UI 之 Buttons 按钮 IconButtons 图标按钮
Buttons 按钮 Android Compose UI 库中的 Button 和 IconButton 是两种常用的组件,它们各自具有一些独特的特点。 Button 的特点: 可点击性:Button 是一个可点击的组件,通常用于触发某个操作或事件。文本内容:Button 通常包含文本内容,用于描述按钮的功能或操作。自定义…...
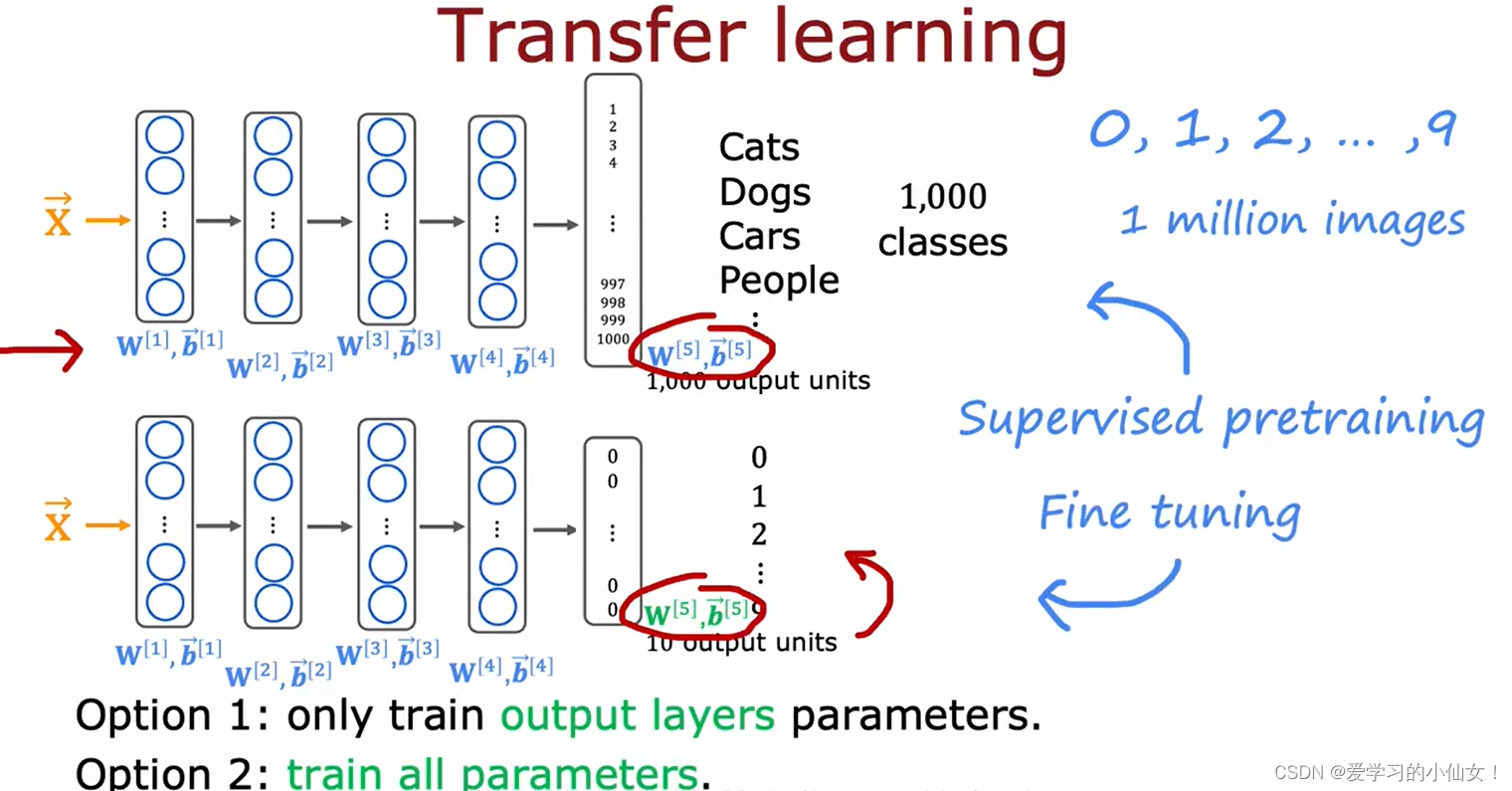
吴恩达机器学习笔记 二十一 迁移学习 预训练
迁移学习(transfer learning):直接把神经网络拿来,前面的参数可以直接用,把最后一层改了。 两种训练参数的方式: 1.只训练输出层的参数 2.训练所有参数 当只有一个小数据集的时候,第一种方法…...

Python中Pandas常用函数及案例详解
Pandas是一个强大的Python数据分析工具库,它为Python提供了快速、灵活且表达能力强的数据结构,旨在使“关系”或“标签”数据的操作既简单又直观。Pandas的核心数据结构是DataFrame,它是一个二维标签化数据结构,可以看作是一个表格…...
VR全景看房:超越传统的看房方式
近年来,新兴技术不断涌出,例如大数据、VR全景、人工智能、元宇宙等。随着科技不断发展,VR全景技术在房地产行业中的应用也是越发广泛,逐渐超越了传统的看房方式。今天,就让我们一起来深入探讨一下VR全景技术在VR看房中…...

pip 配置镜像加速安装
在使用pip安装Python第三方库时,默认是使用pip官网的非常慢,可通过配置国内镜像源加速下载速度,以下是如何使用国内镜像源安装Python库的两种常见方式: 临时使用镜像源安装 如果你只是想临时使用某个镜像源安装单个或几个库&…...

LUA语法复习总结
文章目录 简记变量数据类型运算符算术运算符关系运算符逻辑运算符杂项运算符 列表(表)表格操作表连接插入和删除排序表 模块元表__index 元方法实例 总结__newindex 元方法实例实例 为表添加操作符实例 __call 元方法实例 __tostring 元方法实例 简记 lua下标从1开始迭代器pai…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
