【FMCW 03】测速
从上一讲 测距 末尾的frame讲起。我们知道一个chirp对应了一个采样后的IF信号,我们将这些采样后的IF信号按chirp的次序排列成一个帧(frame),这就得到了我们实际中接收后处理的FMCW信号。
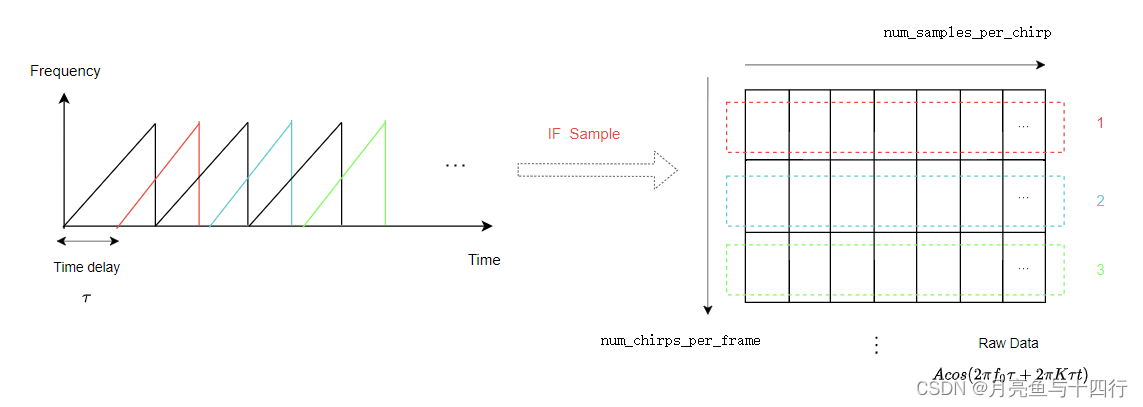
由于chirp的发射返回时间很短,所以我们称其所在时间维度为快时间(fast time)维,而相邻的chirp间存在一个chirp repetition time(CRT)相对较慢,于是我们将其所在时间维度为慢时间(slow time)维。借一幅《Soli: Ubiquitous Gesture Sensing with Millimeter》文中的图,可以对raw signal有一个直观的认识。

相位差的周期性
我们首先对FFT得到的频率谱做一个分析,其分为两部分,幅度部分和相位部分,幅度部分可以表示此处频率的强弱,相位部分表示的是此频率对应的相位。那么,对于,对做完range FFT后的frame矩阵而言,其fast time维度就转换成了range维度。
对于在某一个 range bin上的物体,我们已经知道其距离表示为
dtarget=c2Kfpeakd_{target} = \frac{c}{2K}f_{peak} dtarget=2Kcfpeak
这个距离的解我们知道是通过IF信号中频率部分2πKτ2 \pi K \tau2πKτ得到的,而我们现在关注其相位部分2πf0τ2 \pi f_0 \tau2πf0τ。
xIF(t)=Acos(2πKτt+2πfoτ)x_{\tiny{IF}}(t) = A \cos(2\pi K\tau t+2\pi f_o \tau ) xIF(t)=Acos(2πKτt+2πfoτ)
由于
τ=2dc\tau = \frac{2d}{c} τ=c2d
故相位ϕ\phiϕ
ϕ=2πfo2dc=4πfocd\phi = 2\pi f_o \frac{2d}{c}=\frac{4\pi f_o}{c}d ϕ=2πfoc2d=c4πfod

如果在这个range bin中的物体正在运动,那么每隔一个chirp的周期CRTCRTCRT,物体就会发生一个微动位移,而这个微动位移将造成相位较为剧烈的变化,即
Δϕ=4πfocΔd=4πf0cv⋅CRT\Delta \phi = \frac{4\pi f_o}{c} \Delta d =\frac{4\pi f_0}{c}v \cdot CRT Δϕ=c4πfoΔd=c4πf0v⋅CRT
如果我们将这个CRTCRTCRT看作一种采样,那么,对ϕ\phiϕ的变化进行分析,将能提取到有效的速度vvv的信息,这也正是我们采用frame传输的原因——获得速度信息。 这种视角先按下不表,最后再述。

我们也可将这个过程看作是相位差的周期性运动,那么我们对其进行FFT分析,也将得到这个周期性的相位差信息。
进一步转换到速度维,就有
v=c4πfo⋅CRTΔϕ=λ4π⋅CRTΔϕv = \frac{c}{4\pi f_o \cdot CRT}\Delta \phi =\frac{\lambda}{4 \pi \cdot CRT}\Delta \phi v=4πfo⋅CRTcΔϕ=4π⋅CRTλΔϕ
于是我们要做的Doppler FFT 或者说 Velocity FFT即是取出Range FFT某个range bin对应的一列slow time数据进行FFT。

多普勒效应
那么问题来了,为什么叫Doppler FFT呢?在基本的物理学中,我们曾学习过基本的多普勒效应。举一个生活中的例子,你在街上听到一辆警车向你呼啸而来,你听到警笛的声音是越来越急的(这对应的即是声波的频率越来越高),而当警车越来越远时,你听的警笛是越来越疏的(这对应的即是声波的频率越来越低)。
在这里,我们用一个移动通信中描述移动台所造成的多普勒频偏公式(见Rappaport书中的123页),即
fd=vλcosθf_d = \frac{v}{\lambda}\cos \theta fd=λvcosθ
在FMCW雷达考虑的场景中,取径向速度,即 cosθ=1\cos \theta = 1cosθ=1,同时由于电波一发一收,于是造成的fdf_dfd为
fd=2vλf_d = 2\frac{v}{\lambda} fd=2λv
进一步代入 v 的公式转换为
fd=Δϕ2π⋅CRTf_d = \frac{\Delta \phi}{2 \pi \cdot CRT} fd=2π⋅CRTΔϕ
值得指出的是,主频率部分亦会由于物体的运动产生频偏。但当物体的距离d发生微小的变化时,IF signal 信号的相位变化非常明显,而频率的变化并不显著,远远达不到在CRT的时间内,区分信号的频率。 即相位变化对微动位移有着敏感性。
我们不如用TI教程中的例子来感性认识一下:取 λ=4mm\lambda = 4mmλ=4mm,CRT=40μsCRT = 40 \mu sCRT=40μs,K=50MHz/μsK = 50MHz/\mu sK=50MHz/μs,当物体发生一个1mm的微动位移时,有:
相位变化 Δϕ=4πΔdλ=π=180∘相位变化 \ \Delta \phi = \frac{4 \pi \Delta d}{\lambda} =\pi =180^{\circ} 相位变化 Δϕ=λ4πΔd=π=180∘
频率变化 Δf=2KcΔd=333Hz频率变化 \ \Delta f = \frac{2K}{c} \Delta d=333Hz 频率变化 Δf=c2KΔd=333Hz
而这个频偏在slow time的频率轴引起的变化其实并不大,即
Δf⋅CRT=333×40×10−6=0.013cycles\Delta f \cdot CRT=333\times 40 \times 10 ^{-6} = 0.013 \ cycles Δf⋅CRT=333×40×10−6=0.013 cycles
最大速度与速度分辨率
最大速度
由于Δϕ\Delta \phiΔϕ 的限制,给出了最大速度的限制,即
−π<Δϕ<π-\pi < \Delta \phi < \pi −π<Δϕ<π
于是
−λ4⋅CRT<v<λ4⋅CRT-\frac{\lambda}{4 \cdot CRT} < v <\frac{\lambda}{4 \cdot CRT} −4⋅CRTλ<v<4⋅CRTλ
感性认识一下,比如用 5mm5mm5mm 的毫米波雷达,再用 100μs100 \mu s100μs 的CRT,此时能达到的最大速度为
vmax=λ4⋅CRT=12.5m/sv_{max} = \frac{\lambda}{4 \cdot CRT} =12.5m/s vmax=4⋅CRTλ=12.5m/s
速度分辨率
继续借用TI教程里的一张图(这里定义 ω=Δϕ\omega = \Delta \phiω=Δϕ),容易发现,速度分辨率与我们的在数字域上的角速度分辨率有关,由于
Δω=2πNradians/sample=1Ncycles/sample\Delta \omega = \frac{2\pi}{N} \ radians/sample=\frac{1}{N} \ cycles/sample Δω=N2π radians/sample=N1 cycles/sample

于是就有
Δv=λ4π⋅CRTΔω=λ2N⋅CRT\Delta v = \frac{\lambda}{4 \pi \cdot CRT} \Delta \omega = \frac{\lambda}{2N \cdot CRT} Δv=4π⋅CRTλΔω=2N⋅CRTλ
仍用最大速度中的测算数据,并取 N = 512,我们感性认识到此时的速度分辨率为:
vres=λ2N⋅CRT=0.0488m/sv_{res} = \frac{\lambda}{2N \cdot CRT}=0.0488m/s vres=2N⋅CRTλ=0.0488m/s
基于CRT的采样视角
如果我们基于CRT的采样视角去理解这个相位变化,那么对于式子
Δϕ=4πfocΔd=4πf0cv⋅CRT\Delta \phi = \frac{4\pi f_o}{c} \Delta d =\frac{4\pi f_0}{c}v \cdot CRT Δϕ=c4πfoΔd=c4πf0v⋅CRT
我们两边同除 CRTCRTCRT,就有:
ΔϕCRT=4πf0cv\frac{\Delta \phi}{CRT}=\frac{4\pi f_0}{c}v CRTΔϕ=c4πf0v
根据微分学的知识,我们知道左边可理解为对ϕ\phiϕ的微分,即
w=dϕdt=2πfpeakw = \frac{d\phi}{dt} = 2\pi f_{peak} w=dtdϕ=2πfpeak
于是就有:
fpeak=2vλf_{peak} = 2\frac{v}{\lambda} fpeak=2λv
这个式子说明,从频率轴去看,此时直接测得的就是多普勒频偏。进一步就有:
v=λ2fpeakv =\frac{\lambda}{2 } f_{peak} v=2λfpeak
由于此时 CRTCRTCRT 的倒数即是我们等效的采样率。于是,频率分辨率的范围就在
−12⋅CRT<fpeak<12⋅CRT-\frac{1}{2 \cdot CRT} <f_{peak}<\frac{1}{2\cdot CRT} −2⋅CRT1<fpeak<2⋅CRT1
于是,可得速度的测量范围为
−λ4⋅CRT<v<λ4⋅CRT-\frac{\lambda}{4 \cdot CRT} < v <\frac{\lambda}{4 \cdot CRT} −4⋅CRTλ<v<4⋅CRTλ
和速度的分辨率
vres=λ2fres=λ2N⋅CRTv_{res} =\frac{\lambda}{2 } f_{res} = \frac{\lambda}{2N \cdot CRT} vres=2λfres=2N⋅CRTλ
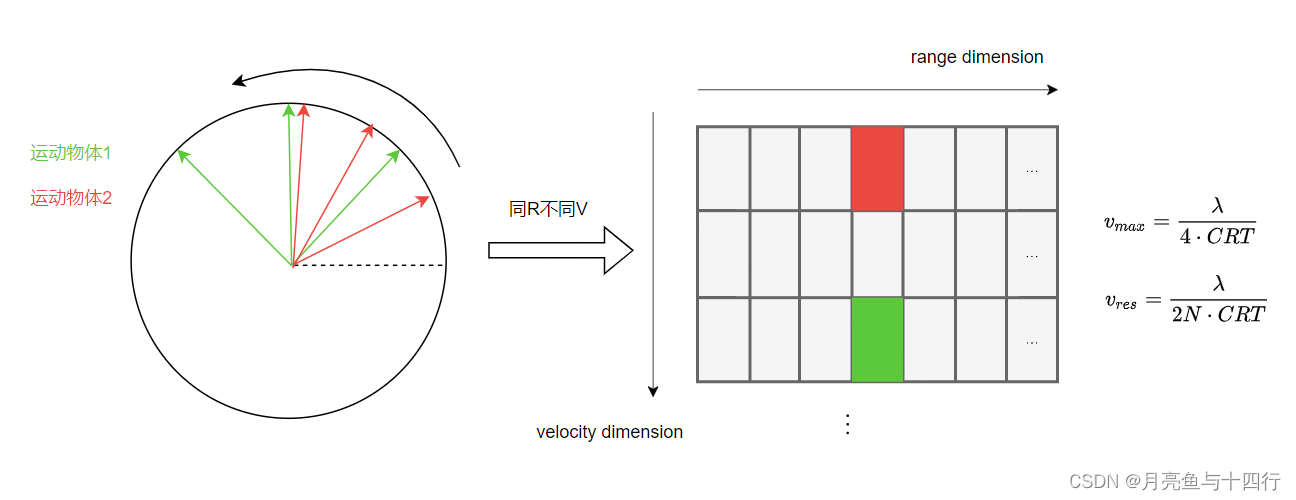
这种视角个人兴趣所至,以增参考。最后,同样用一张图结束本节的内容。
相关文章:

【FMCW 03】测速
从上一讲 测距 末尾的frame讲起。我们知道一个chirp对应了一个采样后的IF信号,我们将这些采样后的IF信号按chirp的次序排列成一个帧(frame),这就得到了我们实际中接收后处理的FMCW信号。 由于chirp的发射返回时间很短,…...
ERP(企业资源管理)概述
🌟所属专栏:ERP企业资源管理🐔作者简介:rchjr——五带信管菜只因一枚😮前言:该系列将持续更新ERP的相关学习笔记,欢迎和我一样的小白订阅,一起学习共同进步~👉文章简介&a…...

深入理解java虚拟机精华总结:性能监控和故障处理工具、类加载机制
深入理解java虚拟机精华总结:性能监控和故障处理工具、类加载机制性能监控和故障处理工具、类加载机制jpsjstatjinfojmapjhatjstackVisualVM类加载机制类加载的时机类加载的过程加载验证准备解析初始化类加载器类与类加载器双亲委派模型破坏双亲委派模型往期内容&am…...

推荐系统与推荐算法
文章目录第一章1.1推荐系统意义与价值1.2推荐系统历史与框架1.3推荐算法分类第二章2.1协同过滤的基本思想与分类2.2基于用户的协同过滤2.3基于项目的协同过滤2.4基于邻域的评分预测2.5基于二部图的协同过滤第三章3.1基于关联规则的推荐3.2基于矩阵分解的评分预测3.3概率矩阵分解…...
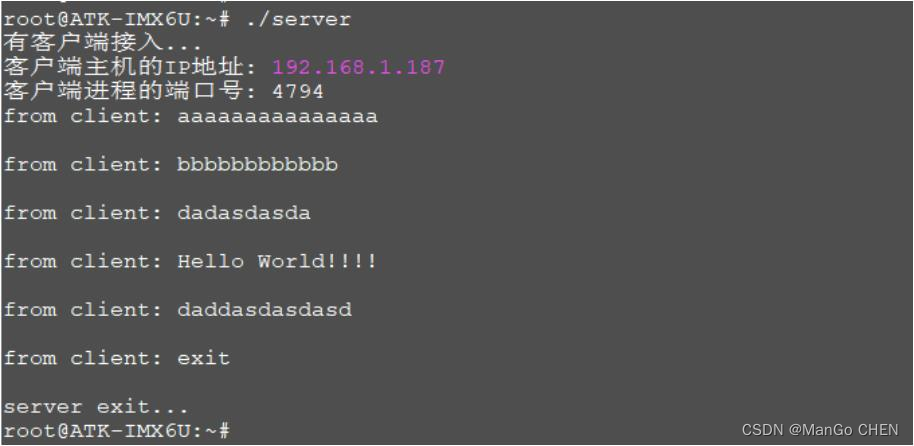
socket 编程实战(编写客户端程序 )
编写客户端程序 接着上一篇:实战服务端程序 接下来我们再编写一个简单地客户端应用程序,客户端的功能是连接上小节所实现的服务器,连接成功之后向服务器发送数据,发送的数据由用户输入。示例代码如下所示: #include…...

“巨亏成名”的魔鬼交易员,你知道几个?
谁说在期货市场上只有赚大钱才能出名?殊不知还有这样一群特殊的交易员靠着巨额亏损而“一战成名”,亏得是老东家元气大伤,外号“魔鬼交易员”——“不亏不成魔”!接下来火象就给大家盘点几位代表性魔鬼交易员,看看他们…...
)
1380:分糖果(candy)
1380:分糖果(candy) 时间限制: 1000 ms 内存限制: 65536 KB 【题目描述】 童年的我们,将和朋友分享美好的事物作为自己的快乐。这天,C小朋友得到了Plenty of candies,将要把这些糖果分给要好的朋友们。已知糖果从一个人传…...

数据挖掘(2.1)--数据预处理
一、基础知识 1.数据的基本概念 1.1基础知识 数据是数据对象(Data Objects)及其属性(Attributes)的集合。 数据对象(一条记录、一个实体、一个案例、一个样本等)是对一个事物或者物理对象的描述。 数据对象的属性则是这个对象的性质或特征,例如一个人的肤色、眼球…...

PMP考前冲刺3.06 | 2023新征程,一举拿证
题目1-2:1.一名团队成员表示,他们的用户故事要等到迭代结束后才能完成,因为他们的职能经理要求他们协助解决高优先级的生产问题。项目经理应该做什么?A.将问题上报给项目发起人以解决和调整项目燃尽图B.与产品负责人讨论用户故事不…...
buuctf-pwn write-ups (11)
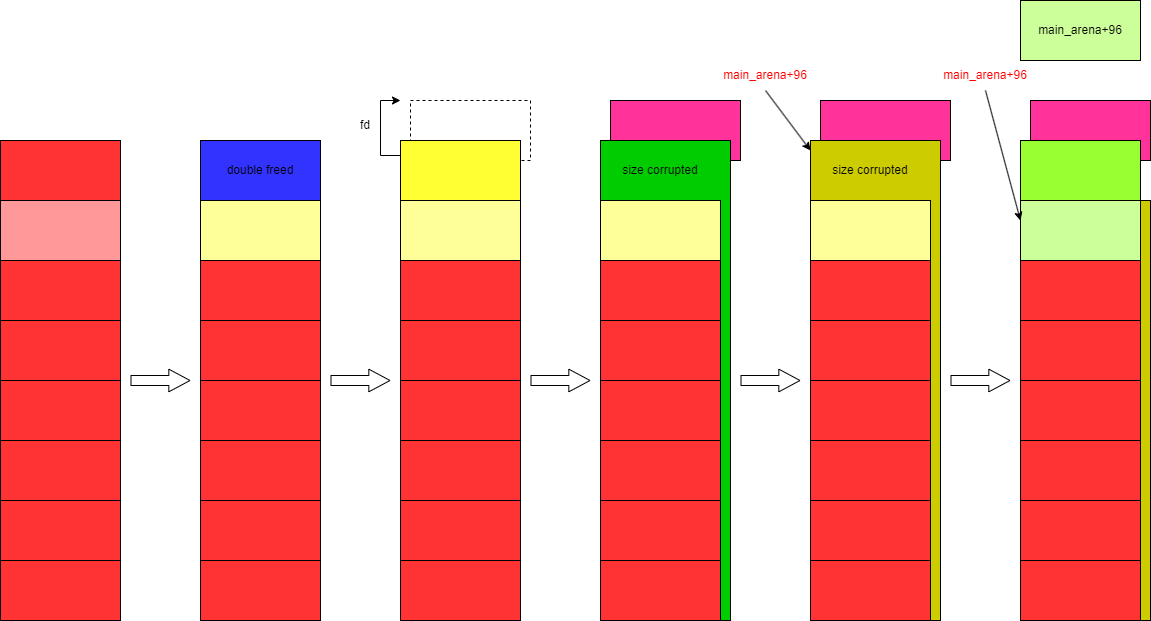
文章目录buu083-x_ctf_b0verfl0wbuu084-picoctf_2018_leak_mebuu085-inndy_echobuu086-hitcontraining_unlinkbuu087-ciscn_2019_final_3buu088-axb_2019_fmt64buu089-wustctf2020_name_your_catbuu090-pwnme1buu091-axb_2019_brop64buu092-[极客大挑战 2019]Not Badbuu083-x_c…...

【VTK】VTK隐藏vtkOutputWindow窗口的正确方法
VTK隐藏vtkOutputWindow窗口 要求隐藏vtkOutputWindow窗口,但是不能把Warning警告和Error错误的信息都给屏蔽了 网上常见的错误方法: 现在百度搜索出来的方法几乎都是在这样做:在main文件中使用vtkOutputWindow::SetGlobalWarningDisplay(0…...

顺序表以及链表的应用及区别(包含OJ讲解)
前面我已经发过怎么实现链表以及顺序表,今天大概的总结一下。 顺序表: 1.能够随时的存取,比较方便。 2.插入删除时,需要挪动数据,比较麻烦,因为是连续存储。 3.存储密度相对于链表来说是比较高的&#…...

JVM简介
一、什么是JVM JVM是Java Virtual Machine(Java虚拟机)的缩写,JVM是一种用于计算设备的规范,它是一个虚构出来的计算机,是通过在实际的计算机上仿真模拟各种计算机功能来实现的。 Java语言的一个非常重要的特点就是与平…...

Leetcode.1653 使字符串平衡的最少删除次数
题目链接 Leetcode.1653 使字符串平衡的最少删除次数 Rating : 1794 题目描述 给你一个字符串 s,它仅包含字符 a和 b 。 你可以删除 s中任意数目的字符,使得 s平衡 。当不存在下标对 (i,j)满足 i < j,且 s[i] b的同…...
leetcode 71~80 学习经历
leetcode 71~80 学习经历71. 简化路径72. 编辑距离73. 矩阵置零74. 搜索二维矩阵75. 颜色分类76. 最小覆盖子串77. 组合78. 子集79. 单词搜索80. 删除有序数组中的重复项 II小结71. 简化路径 给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 &am…...

使用metrics-server监控k8s的资源指标
首先,欢迎使用DHorse部署k8s应用。 k8s可以通过top命令来查询pod和node的资源使用情况,如果直接运行该命令,如下所示。 [rootcentos05 deployment]# kubectl top pod W0306 15:23:24.990550 8247 top_pod.go:140] Using json format to …...

【Copula】考虑风光联合出力和相关性的Copula场景生成(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
【java基础】泛型程序设计基础
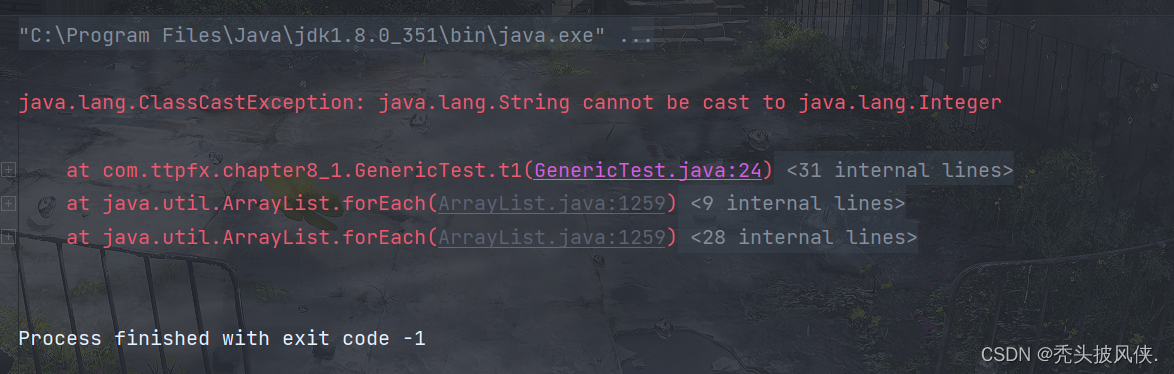
文章目录泛型是什么自定义泛型类自定义泛型方法类型变量的限定总结泛型是什么 泛型类和泛型方法有类型参数,这使得它们可以准确地描述用特定类型实例化时会发生什么。在没有泛型类之前,程序员必须使用Objct编写适用于多种类型的代码。这很烦琐ÿ…...

【省选模拟测试23 T1直径】更好的做法
题目大意和普通做法 省选模拟测试23 T1直径 题解 对于上文中有三个儿子的根节点的树,其直径数量为abbccaabbccaabbcca。那么对于上文中有nnn个儿子的根节点的树,其直径数量为多少呢? 每个儿子所在子树中的点与其他儿子所在子树中的点都能组…...
SpringCloud基础(3)-微服务远程调用
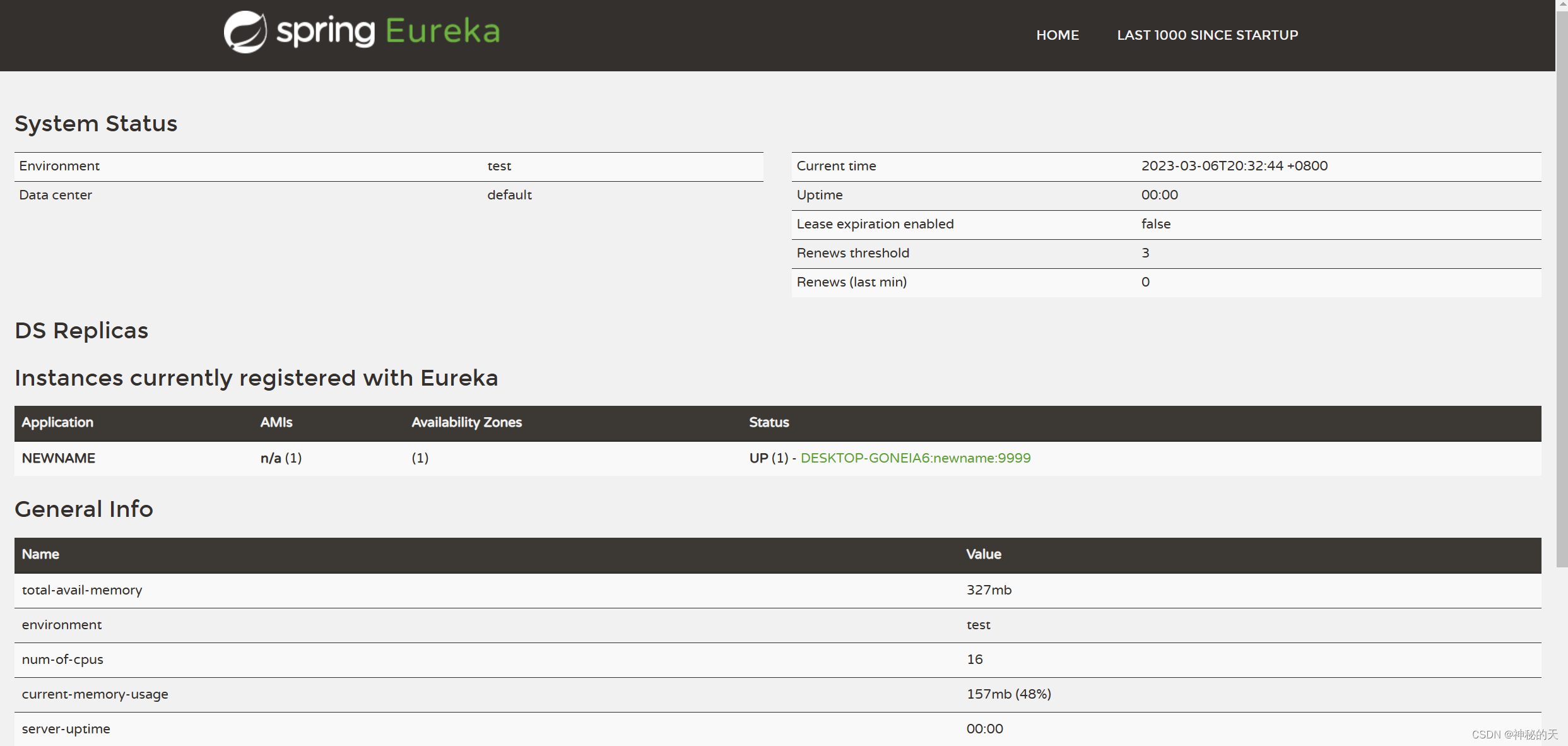
SpringCloud基础1. 微服务的远程调用2. Eureka注册中心1. 搭建Eureka服务注册中心1. 微服务的远程调用 服务提供者:一次业务中被其它服务调用的一方; 服务消费者:一次业务中调用其它服务的一方; 2. Eureka注册中心 记录所有服务…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
