【DL经典回顾】激活函数大汇总(十二)(GLU ReGLU附代码和详细公式)
激活函数大汇总(十二)(GLU & ReGLU附代码和详细公式)
更多激活函数见激活函数大汇总列表
一、引言
欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或缺的角色,它们决定着神经元的输出,并且影响着网络的学习能力与表现力。鉴于激活函数的重要性和多样性,我们将通过几篇文章的形式,本篇详细介绍两种激活函数,旨在帮助读者深入了解各种激活函数的特点、应用场景及其对模型性能的影响。
在接下来的文章中,我们将逐一探讨各种激活函数,从经典到最新的研究成果。
限于笔者水平,对于本博客存在的纰漏和错误,欢迎大家留言指正,我将不断更新。
二、GLU
GLU (Gated Linear Unit) 激活函数是一种通过学习门控机制来动态调节信息流的方法。它在许多深度学习架构中被用来增强模型的表达能力,特别是在序列处理和语言模型中表现出色。
1. 数学定义
GLU激活函数定义为:
GLU ( a , b ) = a ⊙ σ ( b ) \operatorname{GLU}(a, b)=a \odot \sigma(b) GLU(a,b)=a⊙σ(b)
其中:
- a a a和 b b b是相同维度的输入向量。
- ⊙ \odot ⊙表示元素乘法。
- σ ( b ) \sigma(b) σ(b)是对输入 b b b应用Sigmoid激活函数,得到的值在0和1之间,用作门控信号。

2. 函数特性
- 动态门控机制:GLU通过学习 b b b的门控信号来动态地调节 a a a中每个元素的激活强度,这种机制允许模型根据上下文信息自适应地过滤或强化特定的信息流。
- 自适应性强:GLU能够让模型自适应地选择它需要强化或忽略的信息,这有助于模型捕获数据中的复杂依赖关系。
- 非饱和性:由于GLU的输出部分取决于Sigmoid函数,它避免了像ReLU那样的饱和问题,有助于减轻梯度消失问题。
3. 导数
GLU函数关于 a a a和 b b b的导数分别为:
- 对于 a a a: ∂ G L U ∂ a = σ ( b ) \frac{\partial \mathrm{GLU}}{\partial a}=\sigma(b) ∂a∂GLU=σ(b)
- 对于 b b b: ∂ G L U ∂ b = a ⋅ σ ( b ) ⋅ ( 1 − σ ( b ) ) \frac{\partial \mathrm{GLU}}{\partial b}=a \cdot \sigma(b) \cdot(1-\sigma(b)) ∂b∂GLU=a⋅σ(b)⋅(1−σ(b))
这意味着, a a a的梯度受到门控信号 σ ( b ) \sigma(b) σ(b)的调节,而 b b b的梯度则与 a a a的值和门控信号的导数 σ ( b ) ⋅ ( 1 − σ ( b ) ) \sigma(b) \cdot(1-\sigma(b)) σ(b)⋅(1−σ(b))有关。
4. 使用场景与局限性
使用场景:
- 语言模型和序列处理:GLU在处理序列数据,尤其是在构建复杂的语言模型和序列到序列的模型时,能够有效地增强模型的性能。
- 特征选择:在需要模型从大量特征中选择相关信息的任务中,GLU的门控机制可以自适应地过滤掉不重要的特征。
局限性:
- 参数增加:由于GLU对于每个输入都需要一对参数 a a a和 b b b,这可能导致模型参数数量的增加。
- 计算复杂性:相比于一些简单的激活函数,GLU的计算更加复杂,特别是在门控信号需要通过Sigmoid函数计算时。
5.代码实现
import numpy as npdef glu(a, b):"""计算GLU激活函数的值。参数:a -- 输入值,可以是数值、NumPy数组或者多维数组。b -- 门控信号,维度应与a相同。返回:经过GLU激活的结果。"""sigmoid_b = 1 / (1 + np.exp(-b)) # 应用Sigmoid函数到breturn a * sigmoid_b # 返回a和Sigmoid(b)的元素乘结果
解读
- Sigmoid门控:
1 / (1 + np.exp(-b))这行代码对输入b应用Sigmoid函数,将其转换为一个位于(0, 1)区间内的门控信号。这个信号决定了另一输入a的每个元素应该被强化还是被抑制。 - 元素乘法:通过
a * sigmoid_b计算a和Sigmoid处理后的b的元素级乘法,实现GLU的核心功能。这一步骤允许a中的每个元素根据对应的门控信号被按比例调整,实现动态门控。 - 向量化操作:该实现通过使用NumPy,自然地支持向量化操作,使得
glu函数可以直接作用于整个数组,无需显式循环。这对于高效处理大量数据非常关键。
示例使用
# 示例输入
a = np.array([0.5, -1, 2, -2])
b = np.array([1, -1, 0, 2])# 应用GLU激活函数
glu_output = glu(a, b)print("GLU Output:", glu_output)
这个例子展示了如何对两个具有相同维度的输入数组a和b应用GLU激活函数。
三、ReGLU
ReGLU(Rectified GLU)激活函数是一个相对较新的概念,融合了GLU(Gated Linear Unit)的思想与ReLU(Rectified Linear Unit)的特性。GLU是一种通过学习到的门控机制来控制信息流的激活函数,而ReGLU则在此基础上添加了ReLU的非线性特性。
1. 数学定义
假设有两个相同维度的输入向量 a a a和 b b b,ReGLU激活函数定义为:
ReGLU ( a , b ) = ReLU ( a ) ⊙ σ ( b ) \operatorname{ReGLU}(a, b)=\operatorname{ReLU}(a) \odot \sigma(b) ReGLU(a,b)=ReLU(a)⊙σ(b)
其中, ⊙ \odot ⊙表示元素乘法, ReLU ( a ) = max ( 0 , a ) \operatorname{ReLU}(a)=\max (0, a) ReLU(a)=max(0,a)是标准的ReLU函数, σ ( b ) = 1 1 + e − b \sigma(b)=\frac{1}{1+e^{-b}} σ(b)=1+e−b1是Sigmoid函数。
2. 函数特性
- 门控机制:ReGLU通过Sigmoid函数 σ ( b ) \sigma(b) σ(b)作用于 b b b来学习一个门控信号,这个门控信号决定了 a a a的激活强度。
- 非线性激活:通过将ReLU应用于 a a a,ReGLU引入了非线性,有助于增加模型的表达能力。
- 自适应特性:ReGLU的门控机制允许模型自适应地调整信息的流动,这可以根据任务的需求学习到最有效的表示。
3. 导数
ReGLU激活函数的导数相对复杂,因为它涉及到两个不同函数的导数。导数可以通过链式法则计算,分别对 a a a和 b b b进行求导。
4. 使用场景与局限性
使用场景:
- 复杂特征提取:在需要模型学习复杂特征表示的任务中,如深度学习中的图像识别、自然语言处理等领域。
- 动态信息流控制:在模型需要根据数据动态调整信息流的场景中,ReGLU提供了一种有效的机制。
局限性:
- 计算复杂度:由于涉及到Sigmoid和ReLU两个不同的函数,ReGLU的计算复杂度高于单一的激活函数,这可能增加训练和推理的计算成本。
- 参数调优:ReGLU的有效性可能依赖于正确的参数设置和模型架构设计,需要进行细致的调优才能达到最佳性能。
5.代码实现
import numpy as npdef reglu(a, b):"""计算ReGLU激活函数的值。参数:a, b -- 输入值,可以是数值、NumPy数组或者多维数组,维度必须相同。返回:ReGLU激活后的结果。"""relu_a = np.maximum(0, a) # 应用ReLU到asigmoid_b = 1 / (1 + np.exp(-b)) # 应用Sigmoid到breturn relu_a * sigmoid_b # 返回元素乘的结果
解读
- ReLU应用:
np.maximum(0, a)对输入a应用ReLU函数,即对于a中的每个元素,如果元素值大于0,则保持不变;否则,将其设置为0。 - Sigmoid应用:
1 / (1 + np.exp(-b))对输入b应用Sigmoid函数,将b中的每个元素映射到(0, 1)区间内,代表门控信号的强度。 - 元素乘法:最后,通过
relu_a * sigmoid_b计算两个数组的元素级乘法,输出ReGLU激活函数的结果。这个操作实现了一个按元素门控的机制,其中a的激活强度由b学习到的门控信号调节。
示例使用
# 示例输入
a = np.array([1, -2, 3, -4])
b = np.array([5, -1, 2, 3])# 应用ReGLU激活函数
output = reglu(a, b)print("ReGLU Output:", output)
这个例子展示了如何对两个具有相同维度的输入数组a和b应用ReGLU激活函数。
四、参考文献
- Dauphin, Y. N., Fan, A., Auli, M., & Grangier, D. (2017). “Language Modeling with Gated Convolutional Networks.” In Proceedings of the 34th International Conference on Machine Learning (ICML). 这篇论文是GLU在深度学习中应用的重要文献之一,作者展示了在语言模型中使用门控卷积网络(使用GLU)如何有效地提高模型性能。
- Shazeer N. Glu variants improve transformer[J]. arXiv preprint arXiv:2002.05202, 2020.
相关文章:

【DL经典回顾】激活函数大汇总(十二)(GLU ReGLU附代码和详细公式)
激活函数大汇总(十二)(GLU & ReGLU附代码和详细公式) 更多激活函数见激活函数大汇总列表 一、引言 欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或…...

【C++】string类初步介绍
个人主页 : zxctscl 如有转载请先通知 文章目录 1. 为什么学习string类1.1 C语言中的字符串1.2 推荐学习网站 2. 标准库中的string类2.1 string类2.2 string类的常用接口说明2.2.1 constructor2.2.2 遍历string2.2.2.1 下标加[]遍历2.2.2.2 迭代器(itera…...

HCIP --- BGP 综合实验
目录 实验拓扑图: 实验要求: 实验步骤: 1.划分IP地址 R1的配置 R2的配置 R3的配置 R4的配置 R5的配置 R6的配置 R7的配置 R8的配置 2.检测查询IP地址 3.OSPF 建邻 4.查询OSPF 建邻是否成功 5.AS 2 内部BGP 建邻 a. AS 2 内部 IBG…...
【优选算法】专题1 -- 双指针 -- 移动零
前言: 📚为了提高算法思维,我会时常更新这个优选算法的系列,这个专题是关于双指针的练习 🎯个人主页:Dream_Chaser~-CSDN博客 一.移动零(easy) 描述: 「数组分两块」是⾮…...
【计算机视觉】二、图像形成:2、几何基元和几何变换:2D变换
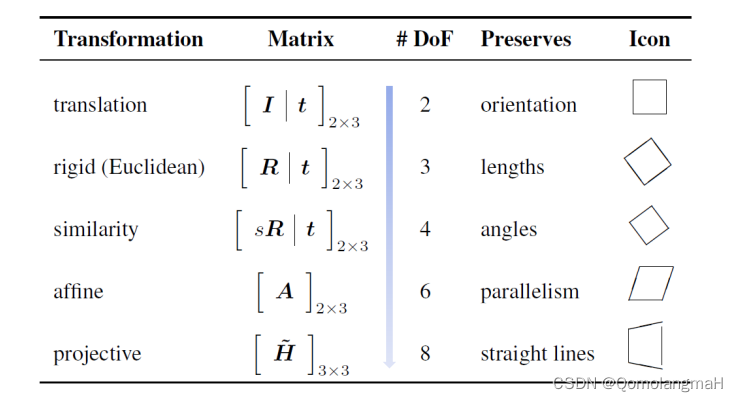
文章目录 一、向量和矩阵的基本运算二、几何基元和变换1、几何基元(Geometric Primitives)2、几何变换(Geometric Transformations)1. 各种变换的关系2. 变换公式3. 2D变换的层次4. python实现 一、向量和矩阵的基本运算 【计算机视觉】二、图像形成:1、向量和矩阵…...
)
蓝桥杯---棋盘(典型的二维差分问题)
题目链接:棋盘 这道题真的是非常典型的二维差分问题了(在我个人看来),题目中的0和1,我们直接让差分数组,偶数就是0,奇数就是1.初始化是0,是白子(偶数)&#x…...
OpenHarmony教程指南—ArkTS时钟
简单时钟 介绍 本示例通过使用ohos.display 接口以及Canvas组件来实现一个简单的时钟应用。 效果预览 使用说明 1.界面通过setInterval实现周期性实时刷新时间,使用Canvas绘制时钟,指针旋转角度通过计算得出。 例如:"2 * Math.PI /…...
uniapp遇到的问题
【uniapp】小程序中input输入框的placeholder-class不生效解决办法 解决:写在scope外面 uniapp设置底部导航 引用:https://www.jianshu.com/p/738dd51a0162 【微信小程序】moveable-view / moveable-area的使用 https://blog.csdn.net/qq_36901092/…...

oppo前端开发一面
提问: 1. 谈谈你怎么实现响应式布局 2. 谈谈你对weback的了解,vite和webpack的区别,webpack loader 3. 你项目怎么用CI/CD(不懂,只知道自动化部署了😭) 4. ts中type和interface区别 5. axi…...
案例分析篇09:Web架构设计相关20个考点(7~11)(2024年软考高级系统架构设计师冲刺知识点总结)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...
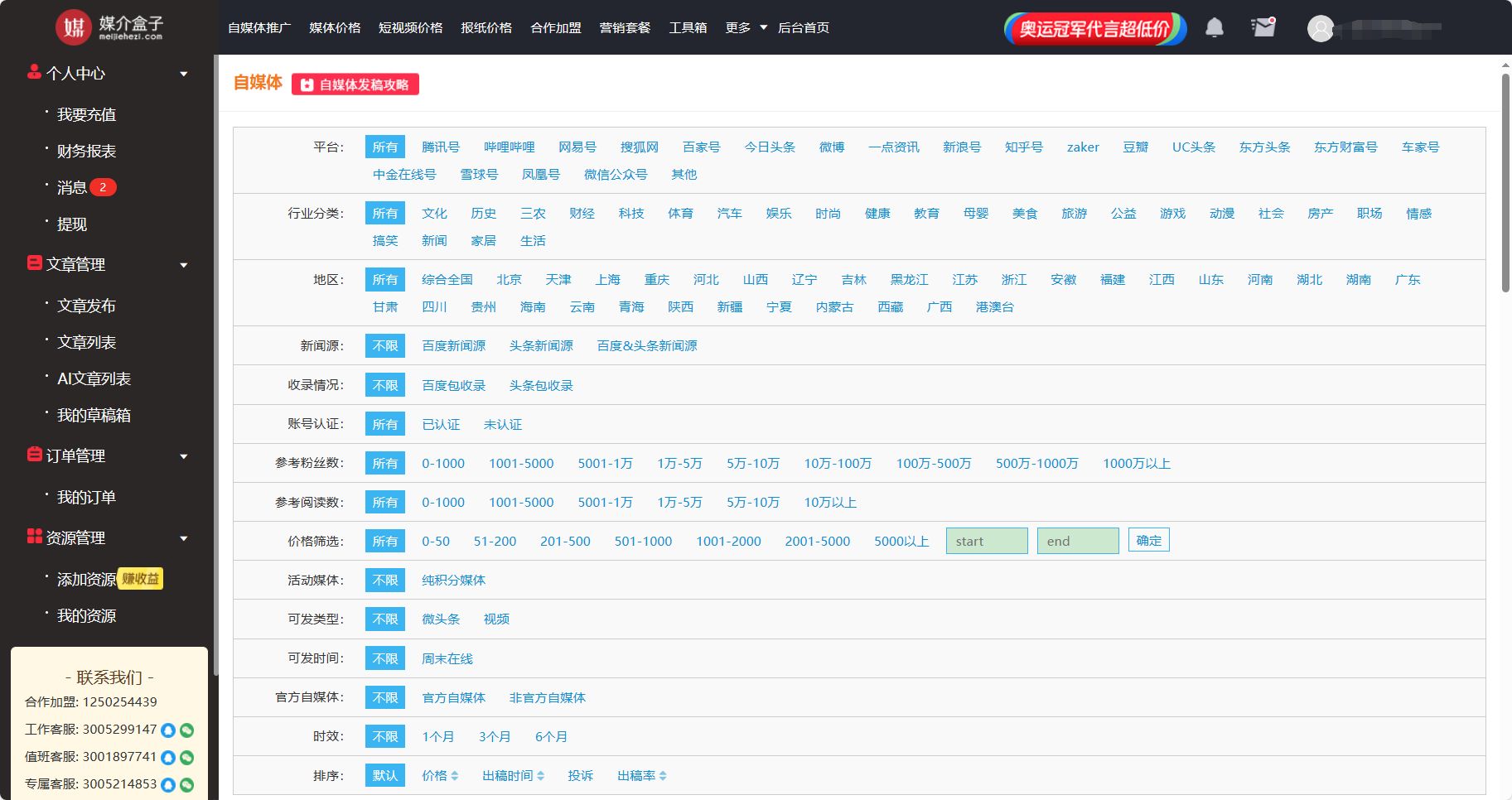
为什么“玄学”与营销联系?媒介盒子分析
在去年有年轻人在上班与上进之中,选择上香,而今年有咖啡品牌买咖啡送木鱼,还有香飘飘在普陀山吸好运,望山楂直接覆盖香火最旺的寺庙,玄学营销的势头甚至盖过了联名营销,呈现节点化的趋势。为什么会这样&…...

C++常用容器总结
容器分为三类,顺序容器,关联容器和适配器。顺序容器又分为连续的容器(vector,array),顺序容器中的离散容器(list,slist,forward_list),离连形的de…...
C# Onnx C2PNet 图像去雾 室外场景
目录 介绍 效果 模型信息 项目 代码 下载 C# Onnx C2PNet 图像去雾 室外场景 介绍 github地址:https://github.com/YuZheng9/C2PNet [CVPR 2023] Curricular Contrastive Regularization for Physics-aware Single Image Dehazing 效果 模型信息 Model P…...

【English Learning】Day13
2024/03/14 和小录打卡的第13天 目录 Words & phrases Words & phrases incrredibly incredibly busy 超级忙merely not merely 不仅仅tragedy a terible tregedy 可怕的悲剧a personal tragedy 个人遭遇strive strive to be best 努力做最好的strive for peace 为和平…...

智障版本GPT3实现
背景,实现GPT3,采用python代码。调库hf及tf2.0+基础。 由于完全实现GPT模型及其预训练过程涉及大量的代码和计算资源,以下是一个基于TensorFlow 2.x的简化版GPT模型构建和调用的示例。请注意,这仅展示了模型的基本结构,实际运行需替换为真实数据集和预处理步骤,且无法直…...
【ubuntu】安装 Anaconda3
目录 一、Anaconda 说明 二、操作记录 2.1 下载安装包 2.1.1 官网下载 2.1.2 镜像下载 2.2 安装 2.2.1 安装必要的依赖包 2.2.2 正式安装 shell 和 base 的切换 2.2.3 检测是否安装成功 方法一 方法二 方法三 2.3 其他 三、参考资料 3.1 安装资料 3.2 验证是否…...

代码随想录|Day20|二叉树09|669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
669. 修剪二叉搜索树 思路:利用二叉搜索树的性质,对于每个节点,判断其是否在区间内: 如果节点值 < low,则此节点和其左子树都不在范围内如果节点值 > high,则此节点和其右子树都不在范围内如果 low &…...

开源的java 代码分析库介绍
本文将为您详细讲解开源的 Java 代码分析库,以及如何安装这些库、它们的特性、区别和应用场景。Java 社区提供了多种代码分析工具,这些工具可以帮助您在 Java 应用程序中进行代码质量评估、性能分析、安全检查等功能。 1. CheckStyle 安装 - 通过…...
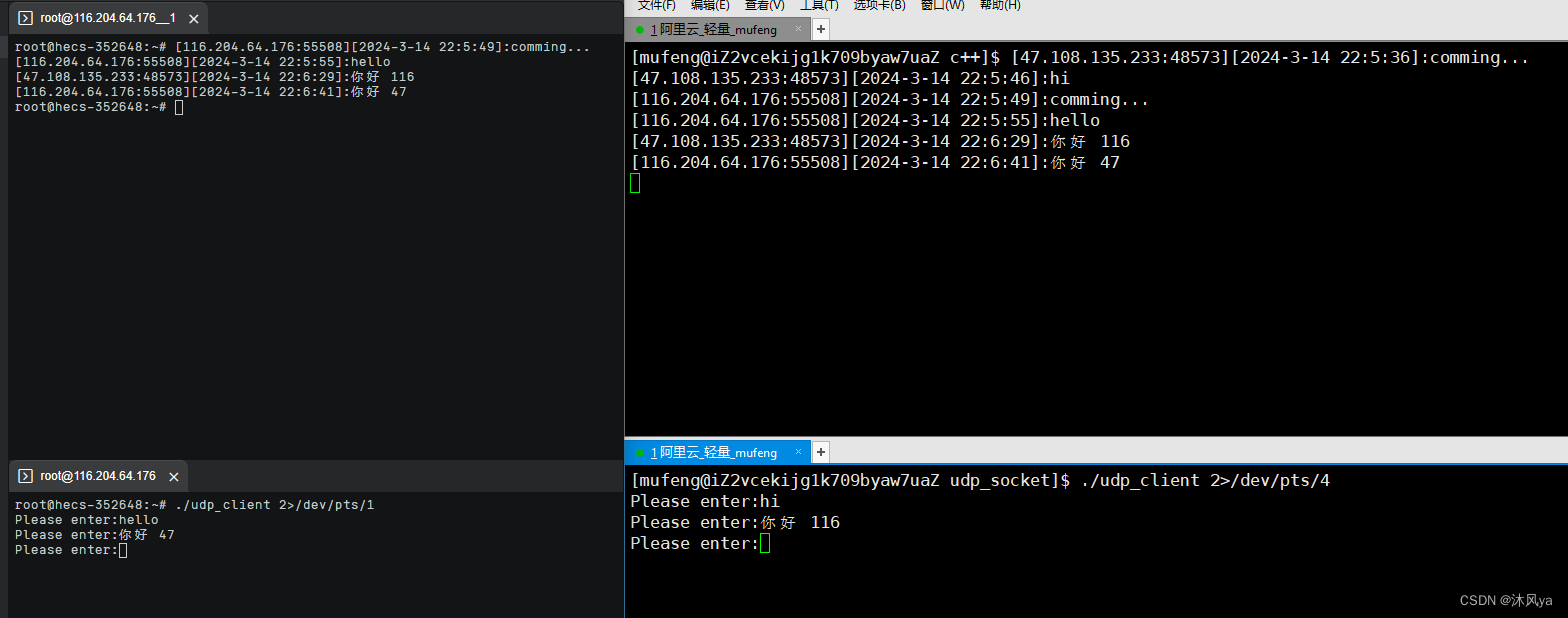
基于udp协议的网络通信(windows客户端版+简易聊天室版),重定向到终端
目录 和windows通信 引入 思路 WSADATA 代码 运行情况 简单的聊天室 思路 重定向 代码 terminal.hpp -- 重定向函数 服务端 客户端 运行情况 和windows通信 引入 linux和windows都需要联网,虽然他们系统设计不同,但网络部分一定是相同的,所以套接字也是一样的 这…...

Qt+FFmpeg+opengl从零制作视频播放器-7.OpenGL播放视频
在上一节Qt+FFmpeg+opengl从零制作视频播放器-6.视频解码中,我们学到了如何将视频数据解码成YUV原始数据,并且保存到本地,最后使用工具来播放YUV文件。 本节使用QOpenGLWidget来渲染解码后的YUV视频数据。 首先简单介绍QOpenGLWidget的使用。 QOpenGLWidget类是用于渲染O…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
