线性代数笔记18--行列式公式、代数余子式
1. 行列式公式推导
二阶行列式推导
[ a b c d ] = [ a 0 c d ] + [ 0 b c d ] = [ a 0 0 d ] + [ a 0 c 0 ] + [ 0 b c 0 ] + [ 0 b 0 d ] = [ a 0 0 d ] − [ b 0 0 c ] = a d − b c \begin{align} \begin{bmatrix} a & b \\ c & d \end{bmatrix}&= \begin{bmatrix} a & 0 \\ c & d \end{bmatrix}+ \begin{bmatrix} 0 & b \\ c & d \end{bmatrix}\nonumber \\ &= \begin{bmatrix} a & 0 \\ 0 & d \end{bmatrix}+ \begin{bmatrix} a & 0 \\ c & 0 \end{bmatrix}+ \begin{bmatrix} 0 & b \\ c & 0 \end{bmatrix}+ \begin{bmatrix} 0 & b \\ 0 & d \end{bmatrix} \nonumber\\ &=\begin{bmatrix} a & 0 \\ 0 & d \end{bmatrix}- \begin{bmatrix} b & 0 \\ 0 & c \end{bmatrix} \nonumber\\ &= ad -bc\nonumber \end{align} [acbd]=[ac0d]+[0cbd]=[a00d]+[ac00]+[0cb0]+[00bd]=[a00d]−[b00c]=ad−bc
三阶行列式推导
[ a b c d e f g h i ] = [ a 0 0 d e f g h i ] + [ 0 b 0 d e f g h i ] + [ 0 0 c d e f g h i ] = [ a 0 0 0 e 0 g h i ] + [ a 0 0 0 0 f g h i ] + [ 0 b 0 d 0 0 g h i ] + [ 0 b 0 0 0 f g h i ] + [ 0 0 c d 0 0 g h i ] + [ 0 0 c 0 e 0 g h i ] = [ a 0 0 0 e 0 0 0 i ] + [ a 0 0 0 0 f 0 h 0 ] + [ 0 b 0 d 0 0 0 0 i ] + [ 0 b 0 0 0 f g 0 0 ] + [ 0 0 c d 0 0 0 h 0 ] + [ 0 0 c 0 e 0 g 0 0 ] = a e i + b f g + c d h − a h f − b d i − c e g \begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i\\ \end{bmatrix} =\begin{bmatrix} a & 0 & 0\\ d & e & f\\ g & h & i\\ \end{bmatrix}+ \begin{bmatrix} 0 & b & 0\\ d & e & f\\ g & h & i\\ \end{bmatrix} +\begin{bmatrix} 0 & 0 & c\\ d & e & f\\ g & h & i\\ \end{bmatrix}\\ =\begin{bmatrix} a & 0 & 0\\ 0 & e & 0\\ g & h & i\\ \end{bmatrix} +\begin{bmatrix} a & 0 & 0\\ 0 & 0 & f\\ g & h & i\\ \end{bmatrix}+ \begin{bmatrix} 0 & b & 0\\ d & 0 & 0\\ g & h & i\\ \end{bmatrix}+ \begin{bmatrix} 0 & b & 0\\ 0 & 0 & f\\ g & h & i\\ \end{bmatrix}+ \begin{bmatrix} 0 & 0 & c\\ d & 0 & 0\\ g & h & i\\ \end{bmatrix}+ \begin{bmatrix} 0 & 0 & c\\ 0 & e & 0\\ g & h & i\\ \end{bmatrix}\\= \begin{bmatrix} a & 0 & 0\\ 0 & e & 0\\ 0 & 0 & i\\ \end{bmatrix}+ \begin{bmatrix} a & 0 & 0\\ 0 & 0 & f\\ 0 & h & 0\\ \end{bmatrix} +\begin{bmatrix} 0 & b & 0\\ d & 0 & 0\\ 0 & 0 & i\\ \end{bmatrix}+ \begin{bmatrix} 0 & b & 0\\ 0 & 0 & f\\ g & 0 & 0\\ \end{bmatrix}+ \begin{bmatrix} 0 & 0 & c\\ d & 0 & 0\\ 0 & h & 0\\ \end{bmatrix} +\begin{bmatrix} 0 & 0 & c\\ 0 & e & 0\\ g & 0 & 0\\ \end{bmatrix} \\= aei+bfg+cdh-ahf-bdi-ceg adgbehcfi = adg0eh0fi + 0dgbeh0fi + 0dg0ehcfi = a0g0eh00i + a0g00h0fi + 0dgb0h00i + 00gb0h0fi + 0dg00hc0i + 00g0ehc0i = a000e000i + a0000h0f0 + 0d0b0000i + 00gb000f0 + 0d000hc00 + 00g0e0c00 =aei+bfg+cdh−ahf−bdi−ceg
行列式公式
d e t A = ∑ j 1 , j 2 , j 3 i s p e r m u t a i o n ± a 1 j 1 a 2 j 2 . . . a n j n ∀ j t 1 , j t 2 ∧ t 1 ≠ t 2 ⇒ j t 1 ≠ j t 2 det\ A=\sum_{j_1,j_2,j_3\quad is\ permutaion}\pm a_{1j_1}a_{2j_2}...a_{nj_n}\\ \forall j_{t_1},j_{t_2} \wedge t_1 \ne t_2 \Rightarrow j_{t_1} \ne j_{t_2} det A=j1,j2,j3is permutaion∑±a1j1a2j2...anjn∀jt1,jt2∧t1=t2⇒jt1=jt2
即选取的列坐标不重复,构成了一个排列。
所以非0项共有 n ! n! n!项。
余子式
M i j : 方阵去掉 i 行 j 列后的方阵的行列式 M_{ij}:方阵去掉i行j列后的方阵的行列式 Mij:方阵去掉i行j列后的方阵的行列式
代数余子式
A i j : ( − 1 ) i + j M i j A_{ij}:(-1)^{i+j}M_{ij} Aij:(−1)i+jMij
方阵行列式:
d e t A = ∑ 1 n A i k , 1 ≤ i ≤ n det\ A=\sum_{1}^{n}A_{ik}, 1 \le i \le n det A=1∑nAik,1≤i≤n
2. 三对角线矩阵
[ 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1 1 ] \begin{bmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 1\\ 0 & 0 & 1 & 1\\ \end{bmatrix} 1100111001110011
∣ A 1 ∣ = 1 |A_1|=1 ∣A1∣=1
∣ A 2 ∣ = 0 |A_2|=0 ∣A2∣=0
∣ A 3 ∣ = − − 1 |A_3|=--1 ∣A3∣=−−1
∣ A 4 ∣ = − 1 |A_4|=-1 ∣A4∣=−1
∣ A 5 ∣ = − 0 |A_5|=-0 ∣A5∣=−0
∣ A 6 ∣ = 1 |A_6|=1 ∣A6∣=1
周期为6
A n A_n An的意思是以 1 , 1 1,1 1,1为起始点的向右向下扩展 k k k个单位的矩阵。
如
A 3 = [ 1 1 0 1 1 1 0 1 1 ] A_3= \begin{bmatrix} 1 & 1 & 0\\1 & 1 & 1 \\0 & 1 & 1 \end{bmatrix} A3= 110111011
相关文章:

线性代数笔记18--行列式公式、代数余子式
1. 行列式公式推导 二阶行列式推导 [ a b c d ] [ a 0 c d ] [ 0 b c d ] [ a 0 0 d ] [ a 0 c 0 ] [ 0 b c 0 ] [ 0 b 0 d ] [ a 0 0 d ] − [ b 0 0 c ] a d − b c \begin{align} \begin{bmatrix} a & b \\ c & d \end{bmatrix}& \begin{bmatrix} a &…...

最新2024年项目基金撰写与技巧及GPT融合应用
随着社会经济发展和科技进步,基金项目对创新性的要求越来越高。申请人需要提出独特且有前瞻性的研究问题,具备突破性的科学思路和方法。因此,基金项目申请往往需要进行跨学科的技术融合。申请人需要与不同领域结合,形成多学科交叉…...

Java八股文(Element Plus)
Java八股文のElement Plus Element Plus Element Plus 什么是Element UI 和 Element Plus? Element UI 和 Element Plus 是基于 Vue.js 的一套非常受欢迎的开源 UI 组件库,用于快速构建具有现代化设计和丰富交互效果的前端界面。 Element UI 和 Element…...
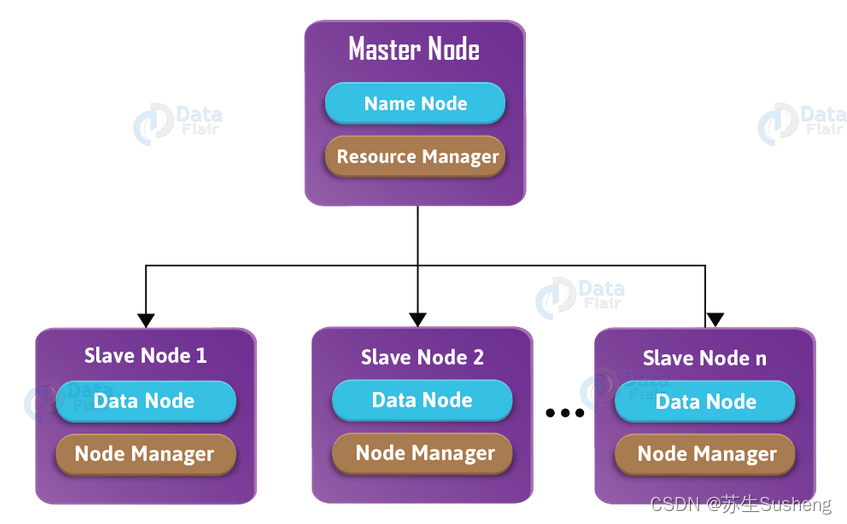
【Hadoop】Hadoop概述与核心组件
目录 Hadoop概述Hadoop 发展历史Hadoop 三大发行版本1.Apache Hadoop(常用)2.Cloudera Hadoop3.Hortonworks Hadoop优势优势总结——4高(高可靠、高扩展、高效、高容错) Hadoop组成1.HDFS管理者:NameNode(n…...
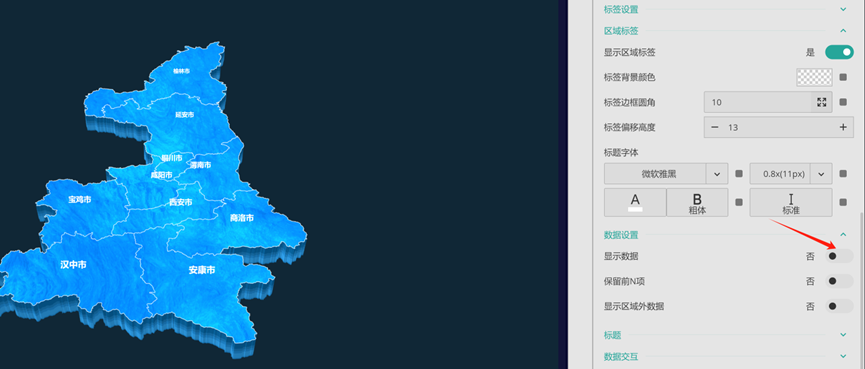
3D地图在BI大屏中的应用实践
前言 随着商业智能的不断发展,数据可视化已成为一项重要工具,有助于用户更好地理解数据和分析结果。其中,3D地图作为一种可视化工具,已经在BI大屏中得到了广泛地应用。 3D地图通过将地理信息与数据相结合,以更加直观…...

JavaScript 进阶(二)
一、深入对象 1.1创建对象三种方式 1. 利用对象字面量创建对象 2. 利用 new Object 创建对象 3.利用构造函数创建对象 1.2 构造函数 构造函数 : 是一种特殊的函数,主要用来初始化对象。 使用场景: 常规的 {...} 语法允许创建一个对象。…...

基于ssm+layui的图书管理系统
基于ssmlayui的图书管理系统 账户类型分为:管理员,用户管理员私有功能用户私有功能公共功能技术栈功能实现图 视频演示 账户类型分为:管理员,用户 图书管理系统主要登录账户类型为管理员账户与用户账户 管理员私有功能 账户管理…...
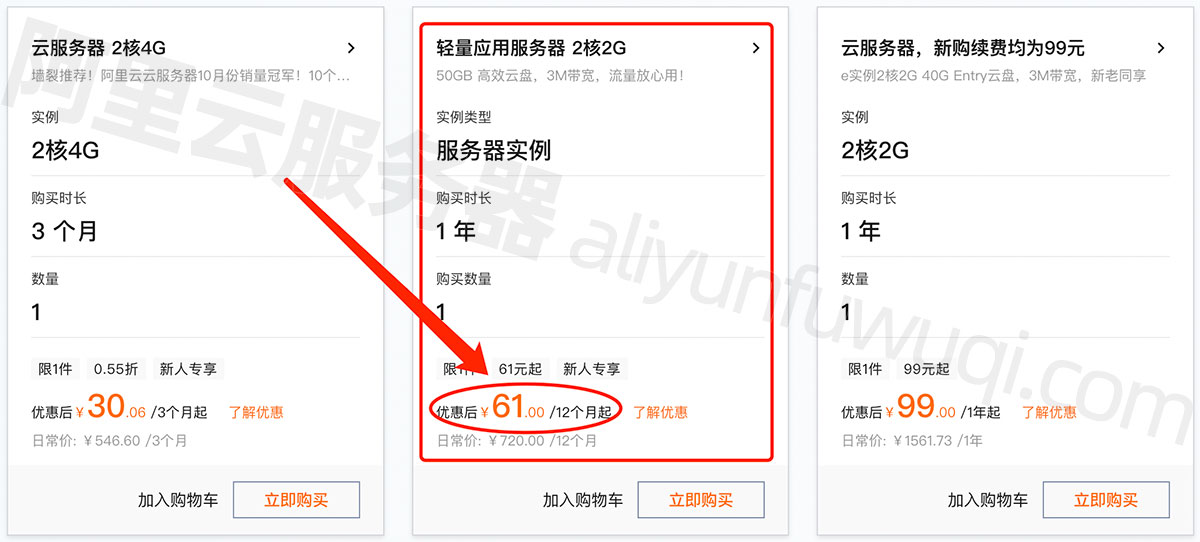
2024年最新阿里云和腾讯云云服务器价格租用对比
2024年阿里云服务器和腾讯云服务器价格战已经打响,阿里云服务器优惠61元一年起,腾讯云服务器61元一年,2核2G3M、2核4G、4核8G、4核16G、8核16G、16核32G、16核64G等配置价格对比,阿腾云atengyun.com整理阿里云和腾讯云服务器详细配…...

双指针算法_复写零
题目: 给一个固定长度的数组arr,将数组中出现的每一个0都复写一遍,并且将其余元素都往右移动 且不要再超过数组长度的位置写入元素,在数组上直接修改 示例: 双数组模拟操作: 从示例来看,因为…...

自习室预订系统|基于springboot框架+ Mysql+Java+B/S架构的自习室预订系统设计与实现(可运行源码+数据库+设计文档+部署说明)
推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 目录 前台功能效果图 学生功能模块 管理员功能登录前台功能效果图 系统功能设计 数据库E-R图设计 lunwen参…...
基于Java+SpringMVC+vue+element宠物管理系统设计实现
基于JavaSpringMVCvueelement宠物管理系统设计实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言 文末获取源…...

用miniconda建立PyTorch、Keras、TensorFlow三个环境
一、配置清华镜像conda源 由于网络问题,直接使用conda默认的源下载包可能会非常慢。为了解决这个问题,可以配置国内镜像源来加速包的下载。清华大学TUNA协会提供了一个常用的conda镜像源。下面是如何配置清华镜像源的步骤: 1. 配置清华conda…...
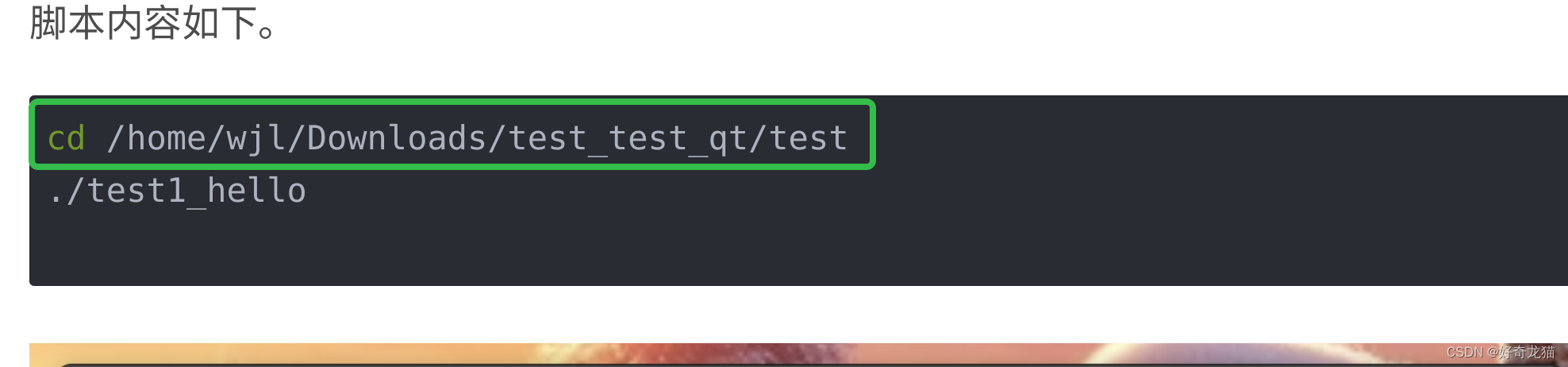
【QT 5 +Linux下qt软件点击.sh脚本运行+Dconf编辑器+学习他人文章+番外篇:点击脚本运行软件】
【QT 5 Linux下qt软件点击.sh脚本运行Dconf编辑器学习他人文章番外篇:点击脚本运行软件】 1、前言2、实验环境3、自我学习总结-本篇总结1、说明:代替qt的快捷方式2、适用性更广3、了解工具:Dconf编辑器注意事项: 4、参考链接-感谢…...

多模态大模型Claude 3正式接入集简云与语聚!对标GPT-4且支持中文
自OpenAI发布GPT-4以来,引发了业务模式与应用使用的巨大变革,掀起了各大企业对于多模态大模型的研究热潮。3月初,AnthropicClaude在官网正式发布Claude 3系列多模态大模型,据了解,该模型在多个维度上超越了GPT-4&#…...

.NET后端返回File文件,及前端处理直接在浏览器下载
后端代码 [AllowAnonymous] public System.Web.Mvc.ActionResult ExportByteExcel(string datatab, string columnnames, string schemecode) { 返回excel。 string ReportName "ExcelTemplete" DateTime.Now.Ticks.ToString(); …...

如何压缩图片文件大小?教大家几种方法
当图片文件较大时,图片压缩可以有效的缩小图片kb,从而使图片储存起来更加方便,也可以解决上传时图片大小被限制的问题,那么我们有什么方法可以简单快速的将图片大小压缩呢?下面就来给大家分享几个如何修改照片大小kb的…...

Qt 如何搭建Lua的运行环境
一、Lua简介 Lua 是一种强大的、高效的、轻量级的、可嵌入的脚本语言。它支持过程(procedural)编程、面向对象编程、函数式编程以及数据描述。Lua 是动态类型的,运行速度快,支持自动内存管理,因此被广泛用于配置、脚本…...
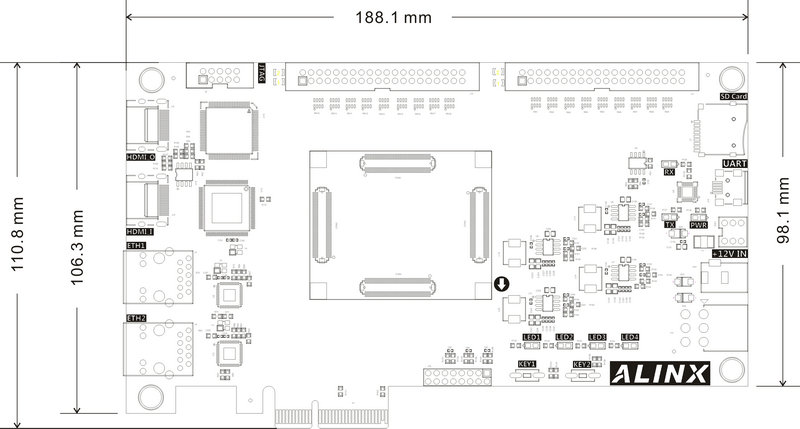
产品推荐 - ALINX XILINX FPGA开发板 Artix-7 XC7A100T-2FGG484I
01开发板介绍 此款开发板采用核心板扩展板的模式,方便用户对核心板的二次开发利用。FPGA使用的是Xilinx公司的ARTIX-7系列的芯片,型号为XC7A100T-2FGG484I。在核心板使用了2片MICRON公司的MT41J256M16HA-125 DDR3芯片,组合成32bit的数据总线…...
Github 2024-03-16 开源项目日报Top10
根据Github Trendings的统计,今日(2024-03-16统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目5非开发语言项目2TypeScript项目1C++项目1Lua项目1Swift项目1《Hello 算法》:动画图解、一键运行的数据结构与算法教程 创建周期:4…...

【使用postman测试python接口】
打开python服务 设置postman如下,并发送: postman新建请求设置请求方式为post设置地址、raw、json方式、内容如下 结果: python如下: from flask import Flask, request, jsonifyapp Flask(__name__) # 实例化对象app.route…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
