C++笔记:从零开始一步步手撕高阶数据结构AVL树
文章目录
- 高度平衡二叉搜索树
- 实现一颗AVL树
- 结点与树的描述——定义类
- AVL树的插入操作
- 步骤1:按照二叉搜索树的方法插入结点
- 步骤2:自底向上调整平衡因子
- 步骤3:触发旋转操作(AVL树平衡的精髓)
- 右单旋
- 左单旋
- 左右双旋
- 右左双旋
- 验证AVL树是否平衡
- 参考文章
高度平衡二叉搜索树
二叉搜索树是一种特殊的树形数据结构,一般情况下,该树能够缩短查找的效率,但是它有个缺陷,在结点的插入或删除顺序较为特殊时结构会退化成链表,导致搜索、插入和删除等操作的时间复杂度从O(log n)退化到O(n)。
【二叉搜索树退化成链表的例子】
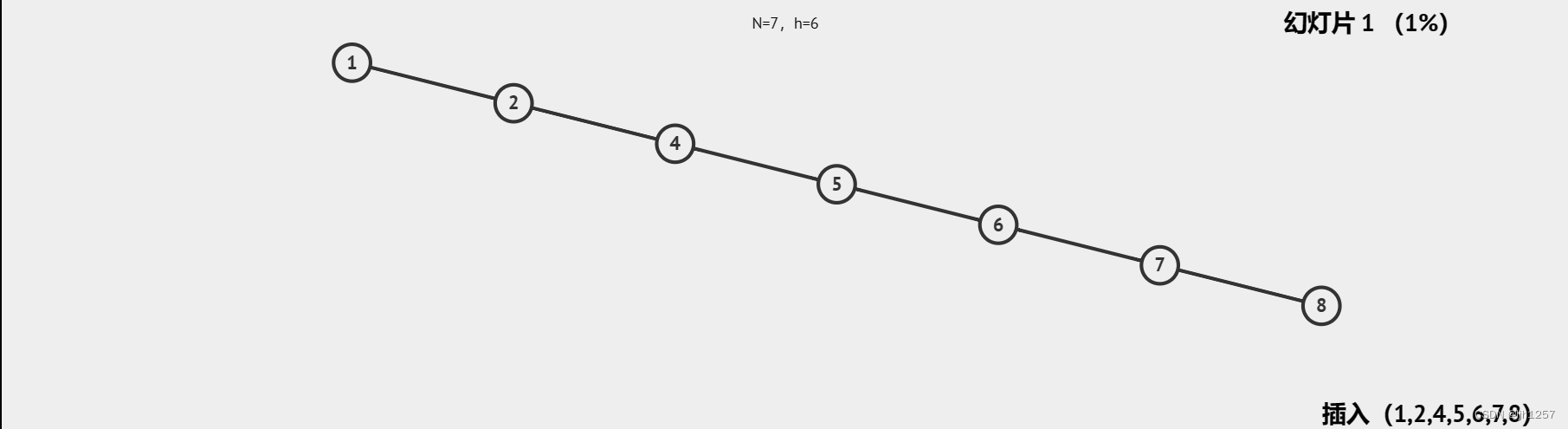
高度平衡二叉搜索树是针对二叉搜索树的缺陷所发明出来的一种改良结构。
高度平衡二叉搜索树常被称为 “ AVL树 ”,这主要是为了纪念发明它两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis,AVL是两位数学家的名字的缩写。
一颗AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 左右子树高度之差(简称为平衡因子)的绝对值不超过1。
- 在这里平衡因子的求法定义为:右子树的高度 - 左子树的高度。
- 结点的左右两棵子树也都是一棵平衡二叉树。


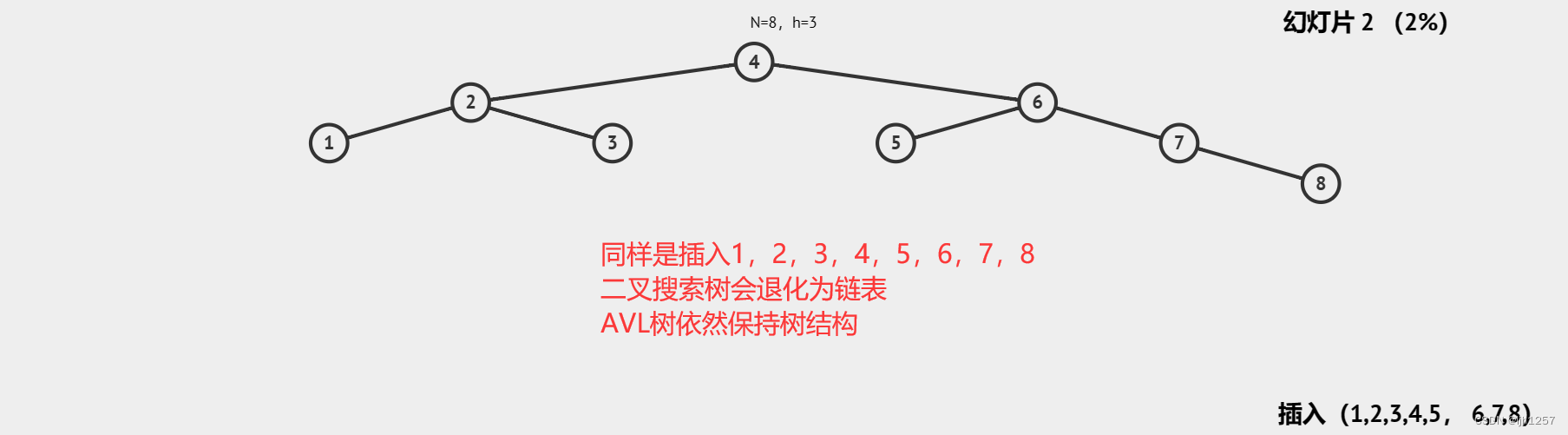
实现一颗AVL树
概念部分讲的差不多了,至于AVL树相较于二叉搜索树是如何保持平衡结构,就在接下来的实现过程中一步步讲解。
结点与树的描述——定义类
namespace ljh
{template<class K, class V>struct AVLTreeNode{AVLTreeNode(const pair<K, V> kv) : _kv(kv) {}AVLTreeNode<K, V>* _parent = nullptr; // A pointer to node's fatherAVLTreeNode<K, V>* _left = nullptr; // A pointer to node's left childAVLTreeNode<K, V>* _right = nullptr; // A pointer to node's right childint _bf = 0; // balance factorpair<K, V> _kv; // key-value};template<class K, class V>class AVLTree{typedef AVLTreeNode<K, V> Node;public:// AVL树的操作方法protected:Node* _root = nullptr;};
}
【说明】
- 模板化设计:
- 使用
template<class K, class V>来定义AVLTreeNode和AVLTree,使得该数据结构能够处理任意类型的键(Key)和值(Value),提高了代码的复用性和灵活性。 K代表键的类型,V代表值的类型。使用者可以根据自己的需求,在AVL树存储任何类型的键值对。
- 使用
- AVLTreeNode类:
AVLTreeNode结构体定义了AVL树中每个节点的结构,用struct定义是为了方便在树类访问。_parent指针:指向父节点,用于在旋转等操作中快速定位父节点(记住这里的旋转,这将是后面的重点)。_left和_right指针:分别指向左孩子和右孩子,是二叉树结构的基础。_bf(平衡因子):存储节点的平衡因子,用于衡量树是否平衡。_kv:存储于结点中的键值对,其中K是键的类型,V是值的类型。
- 构造函数:
AVLTreeNode的构造函数接收一个pair<K, V>对象,并初始化_kv成员变量。这样,当创建新节点时,可以方便地传入键值对。
- AVLTree类:
AVLTree类代表整个AVL树结构。typedef AVLTreeNode<K, V> Node;,在内部使用定义了一个类型别名Node,目的是简化代码书写。_root指针:指向AVL树的根节点,是整棵树的入口点。
- 保护成员:
_root成员变量被设计为protected,意味着它只能在AVLTree类及其派生类中被访问。这种设计是为了将AVL树的内部实现细节隐藏起来,而只暴露必要的公共接口给外部使用。
- 命名空间:
- 为了方便使用库函数,使用
using namespace std;展开标准库,但这容易引发同名类或函数发生冲突,因而将所有定义放在ljh命名空间中。
- 为了方便使用库函数,使用
AVL树的插入操作
AVL树的插入操作实现起来大致分成以下三个大步骤
步骤1:按照二叉搜索树的方法插入结点
- 树为空,则构造新结点,让_root 指针指向该结点,返回
true。 - 树不空,按key的大小寻找插入位置,如果已存在,按插入失败处理,返回
false。 - 走到空表示找到合适位置,然后插入构造的新结点,插入时要判断左边插入或者右边插入。
此时插入并未结束,接下来进行步骤二的平衡因子更新操作!
【步骤1的代码如下:】
bool insert(pair<K, V> kv)
{// empty tree -> 直接插入if(_root == nullptr){_root = new Node(kv);return true;}// not empty tree -> 找到合适的位置再插入else{Node* child = _root;Node* parent = nullptr;while (child){// 大,往右走if (child->_kv.first < kv.first){parent = child;child = child->_right;}// 小,往左走else if (child->_kv.first > kv.first){parent = child;child = child->_left;}// 相同,插入失败else{return false;}}// child == nullptr, 找到合适的位置child = new Node(kv);if (child->_kv.first > parent->_kv.first) parent->_right = child;else parent->_left = child;child->_parent = parent;// 自底向上更新平衡因子// ...}
}
步骤2:自底向上调整平衡因子
我们将新插入结点称为child,新插入结点的双亲结点称为parent。
平衡因子的更新规则如下:
- 如果
child是parent的左孩子,parent的平衡因子-1。 - 如果
child是parent的右孩子,parent的平衡因子+1。
这是第一次更新,更新完之后要不要继续向上更新取决于以parent为根结点的这棵树的高度是否变化,情况有以下3种:
-
平衡因子更新后,
parent的平衡因子为0:
这意味着parent->_bf是从-1 -> 0或者从1 -> 0,以parent为根结点的这棵树的高度没有发生变化,不用再向上更新平衡因子,可以返回true,表示插入成功。 -
平衡因子更新后,
parent的平衡因子为-1或+1:
这意味着parent->_bf是从0 -> -1或者从0 -> 1,以parent为根结点的这棵树的高度发生了变化,但还没有达到需要旋转的程度。
在这种情况下,更新child = child->_parent,更新parent = parent->_parent,继续更新parent的平衡因子,直到情况1:找到平衡因子为0的节点;或者情况2:到达根节点(parent == nullptr)。 -
平衡因子更新后,
parent的平衡因子为-2或+2:
这意味着此时以parent为根结点的这棵树已经违反了AVL树的规则,需要进行旋转处理,处理完之后,可以直接返回true。
【步骤2的代码如下:】
// 自底向上更新平衡因子
while (parent)
{if (child == parent->_left){--parent->_bf;}else{++parent->_bf;}if (parent->_bf == 0){return true;}else if (parent->_bf == 1 || parent->_bf == -1){child = child->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 违反规则,旋转处理// ...}else{// 理论上没错误不会走到这里assert(false);}
}
步骤3:触发旋转操作(AVL树平衡的精髓)
根据节点插入位置的不同,AVL树的旋转分为以下4种:
由于具象图的种类繁多,根本不可能画得完,下面AVL树旋转的图解中大多画的是抽象图。
右单旋
这里给出了一棵以结点90作为根节点的AVL树的抽象图,图中 a / b / c 代表三棵高度为 h 的子树。
这颗AVL树的左子树高度高于右子树高度。

首先,以90为根结点的这棵树有三种可能:
- 它是某棵AVL树的左子树;
- 它是某棵AVL树的右子树;
- 它就是AVL树的根结点;
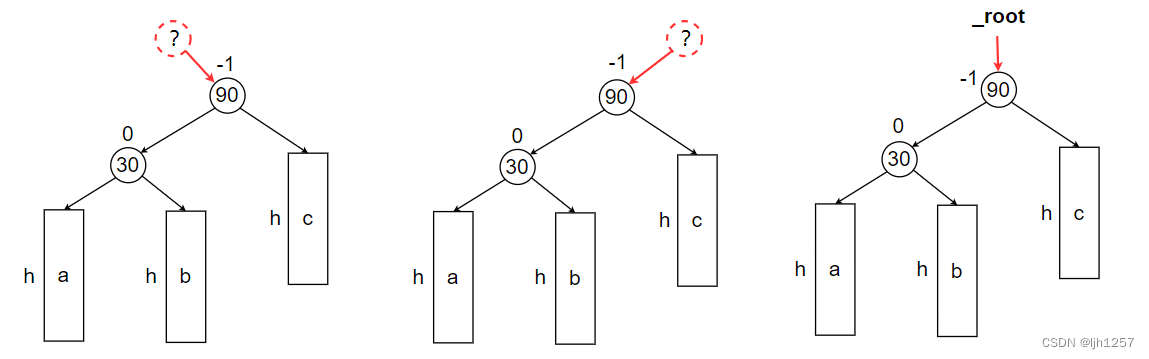
当新结点插入在了较高左子树的左侧,即 a 子树时,child 和 parent 自底向上更新平衡因子,当出现parent->_bf == -2, child->_bf == -1时,该树违反了AVL树的规则,需要进行右单旋操作。

在右单旋中,涉及到改变链接关系的结点主要有以下4个:

当 a / b / c 3棵子树高度为零时插入新结点,平衡因子为 -2 的结点向右旋转:

当 a / b / c 3棵子树高度不为零时插入新结点,平衡因子为 -2 的结点向右旋转:
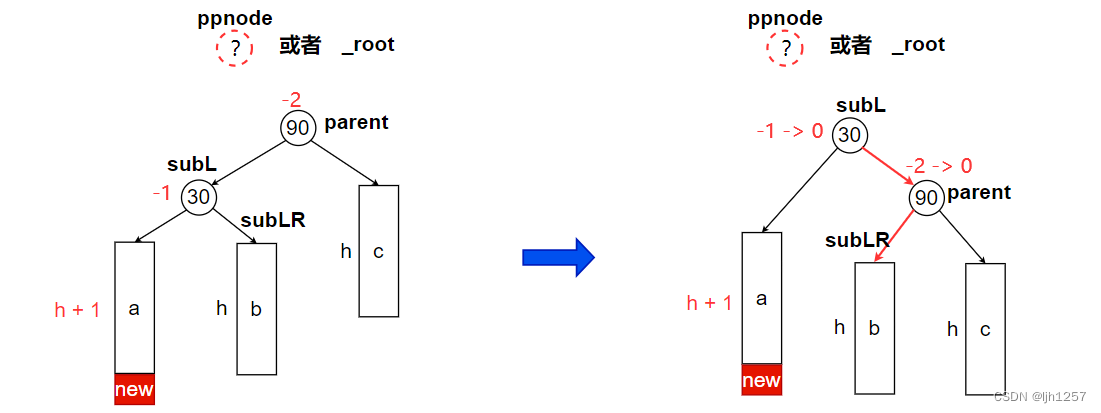
【右单旋操作的代码如下】
void R_Rotate(Node* parent)
{Node* ppnode = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;// subL and parentsubL->_right = parent;parent->_parent = subL;// parent and subLRparent->_left = subLR;if (subLR) subLR->_parent = parent;// ppnode and subLif (ppnode == nullptr){_root = subL;subL->_parent = nullptr;}else{subL->_parent = ppnode;if (parent == ppnode->_left){ppnode->_left = subL;}else{ppnode->_right = subL;}}parent->_bf = subL->_bf = 0;
}
左单旋
这里给出了一棵以结点30作为根节点的AVL树的抽象图,图中 a / b / c 代表三棵高度为 h 的子树。
这颗AVL树的右子树高度高于左子树高度。

首先,以30为根结点的这棵树有三种可能:
- 它是某棵AVL树的左子树;
- 它是某棵AVL树的右子树;
- 它就是AVL树的根结点;
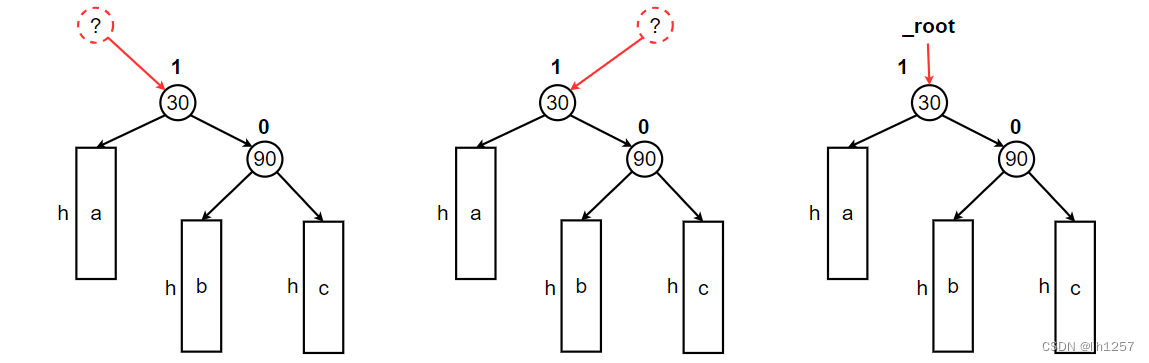
当新结点插入在了较高右子树的右侧,即 c 子树时,child 和 parent 自底向上更新平衡因子,当出现parent->_bf == 2, child->_bf == 1时,该树违反了AVL树的规则,需要进行左单旋操作。
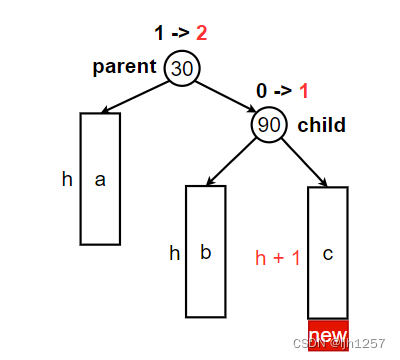
在左单旋中,涉及到改变链接关系的结点同样有4个:

当 a / b / c 3棵子树高度为零时插入新结点,平衡因子为 2 的结点向左旋转:
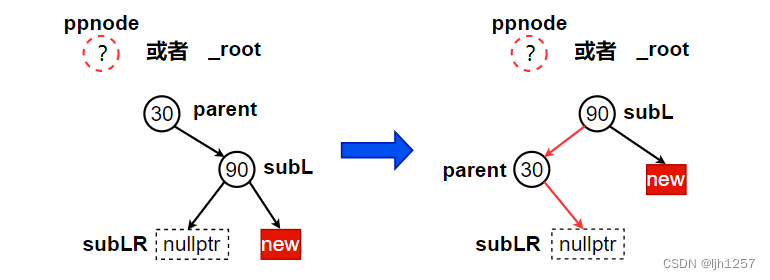
当 a / b / c 3棵子树高度不为零时插入新结点,平衡因子为 2 的结点向左旋转:
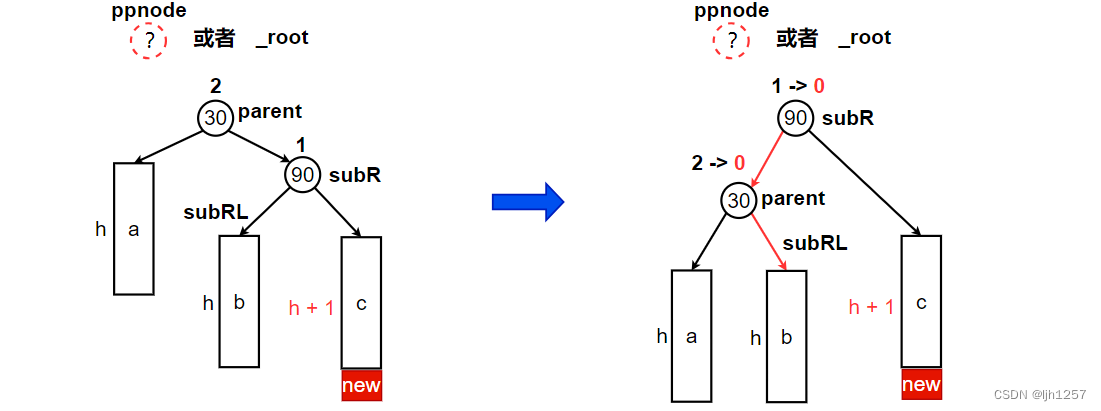
【左单旋操作的代码如下】
void L_Rotate(Node* parent)
{Node* ppnode = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;// subR and parentsubR->_left = parent;parent->_parent = subR;// parent and subRLparent->_right = subRL;if (subRL) subRL->_parent = parent;//ppnode and subRif (ppnode == nullptr){_root = subR;subR->_parent = nullptr;}else{subR->_parent = ppnode;if (parent == ppnode->_left){ppnode->_left = subR;}else{ppnode->_right = subR;}}parent->_bf = subR->_bf = 0;
}
左右双旋
这里给出了一棵以结点90作为根节点的AVL树的抽象图,图中 a / b / c / d 代表四棵子树。
这颗AVL树的左子树高度高于右子树高度。
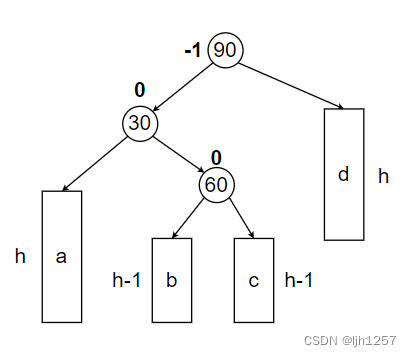
首先,以90为根结点的这棵树有三种可能:
- 它是某棵AVL树的左子树;
- 它是某棵AVL树的右子树;
- 它就是AVL树的根结点;
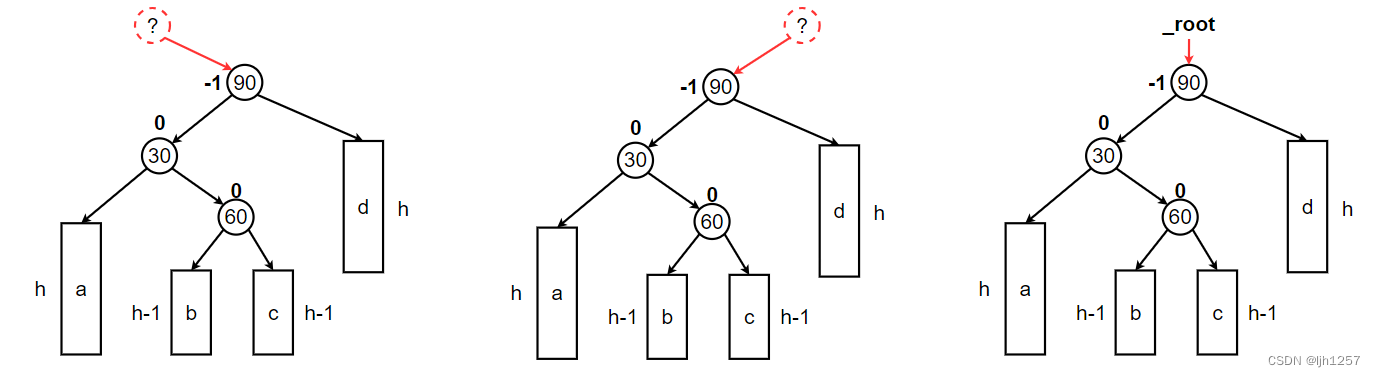
下面三种情况都有一个共同给特点,就是parent->_bf == -2, child->_bf == 1。
我们不难发现,左右双旋可以视为先左旋再右旋,即结点30先左旋,结点90再右旋。


单旋中的subLR不管怎么操作,它的平衡因子都是 0,但是在双旋中,subLR有可能是 -1、0、1中任意一种,因此,虽然双旋操作我们可以复用单旋的代码,但是双旋之后的平衡因子调整需要单独处理。
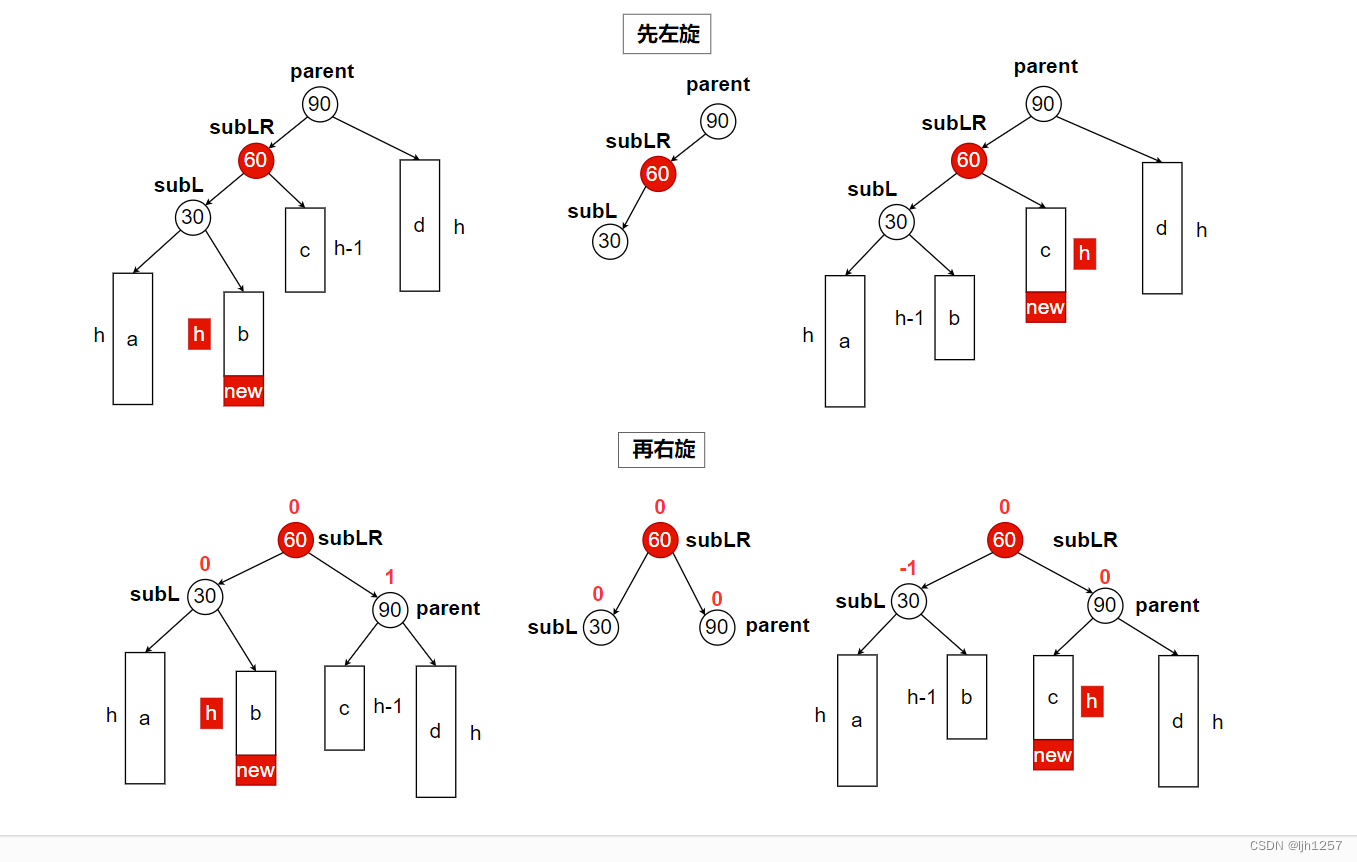
【左右双旋的代码如下】
void LR_Rotate(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;// 双旋之后要靠bf来更新平衡因子int bf = subLR->_bf;L_Rotate(subL);R_Rotate(parent);if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else{subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}
}
右左双旋
这里给出了一棵以结点30作为根节点的AVL树的抽象图,图中 a / b / c / d 代表四棵子树。
这颗AVL树的右子树高度高于左子树高度。
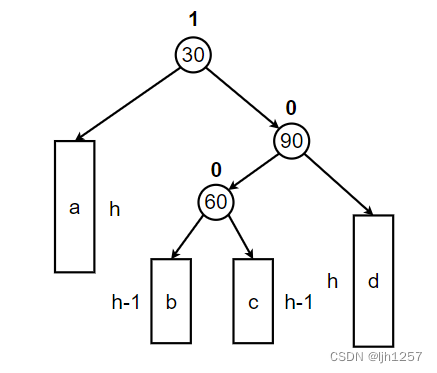
首先,以30为根结点的这棵树有三种可能:
- 它是某棵AVL树的左子树;
- 它是某棵AVL树的右子树;
- 它就是AVL树的根结点;

下面三种情况都有一个共同给特点,就是parent->_bf == 2, child->_bf == -1。
我们不难发现,右左双旋可以视为先右旋再左旋,即结点90先右旋,结点30再左旋。
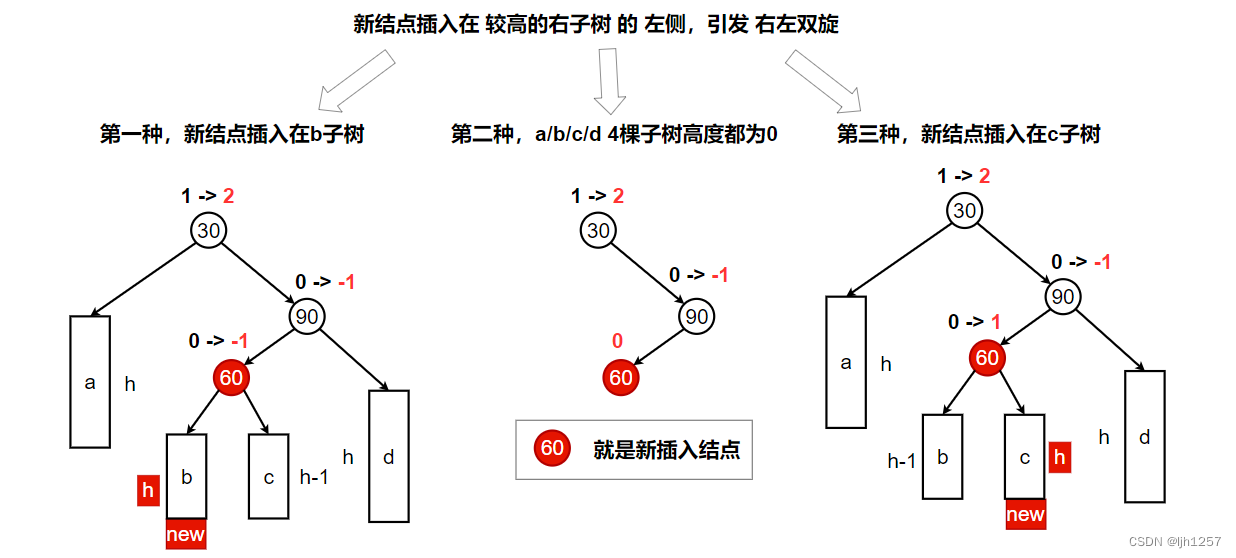

单旋中的subRL不管怎么操作,它的平衡因子都是 0,但是在双旋中,subRL有可能是 -1、0、1中任意一种,因此,虽然双旋操作我们可以复用单旋的代码,但是双旋之后的平衡因子调整需要单独处理。
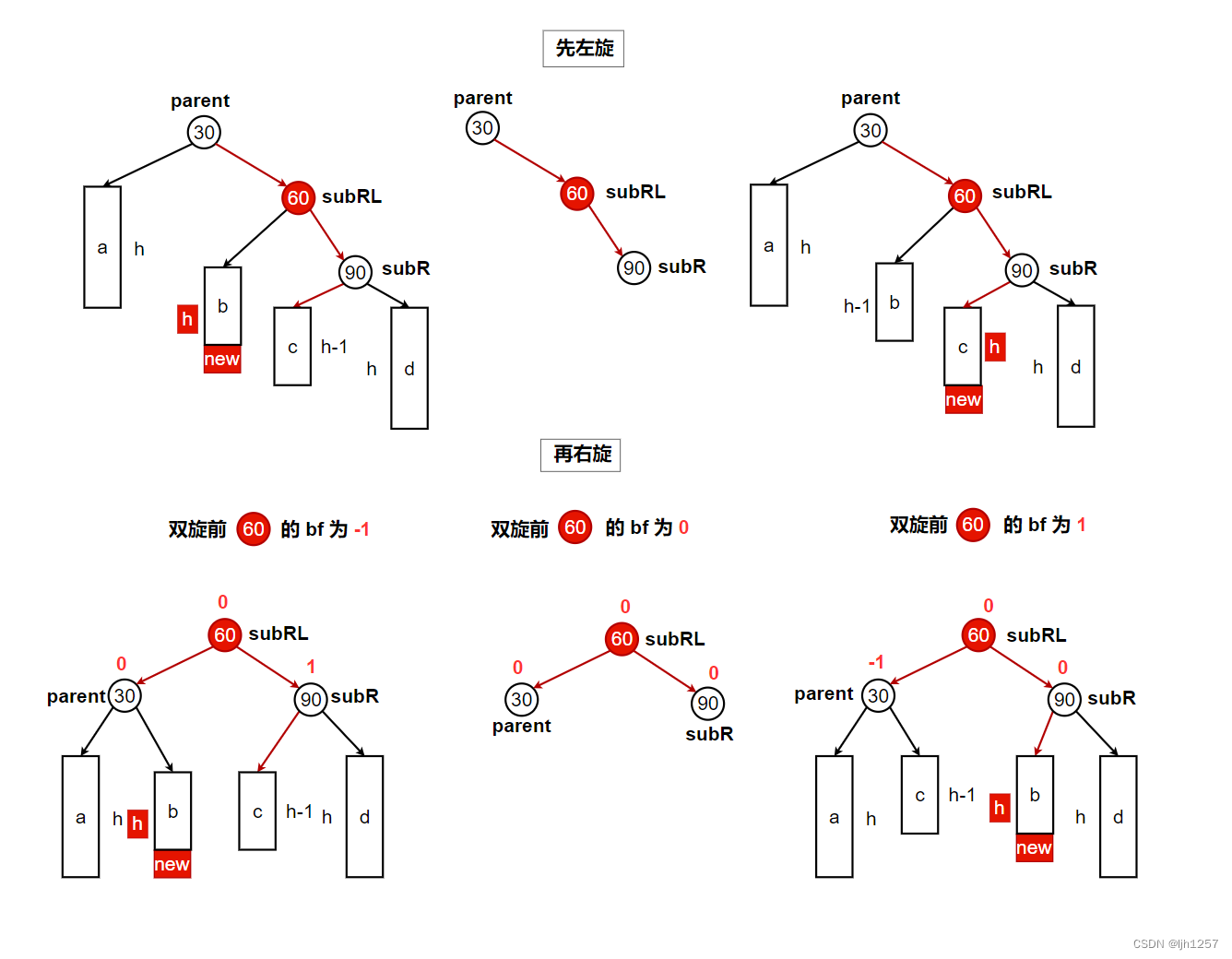
【右左双旋的代码如下】
void RL_Rotate(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;// 双旋之后要靠bf来更新平衡因子int bf = subRL->_bf;R_Rotate(subR);L_Rotate(parent);if (bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else{subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}
}
验证AVL树是否平衡
虽然目前已经将AVL树的插入操作的代码已经写出来了,但是仅仅是写出来了一定能够保证代码就是正确的吗——肯定不是!
所以,接下来还要再实现一个方法,来验证一棵AVL树是不是平衡的。
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树。 - 验证其为平衡树
每个结点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)。
结点的平衡因子是否计算正确。
【写法一代码:简单但是效率低】
// 求AVL树的高度
size_t _Height(Node* root)
{if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}size_t Height()
{return _Height(_root);
}bool _IsBalance(Node* root)
{// 空树也是AVL树if (root == nullptr) return true;// 计算root节点的平衡因子:即root左右子树的高度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者// root平衡因子的绝对值超过1,则一定不是AVL树int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "不平衡" << endl;return false;}if (diff != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}// root的左和右如果都是AVL树,则该树一定是AVL树return _IsBalance(root->_left) && _IsBalance(root ->_right);
}
【写法二代码:效率高但是相较写法一难理解】
// 判断AVL树是否平衡,高效
bool _IsBalance(Node* root, int& height)
{// 空树也是AVL树if (root == nullptr){height = 0;return true;}// 后序递归,leftHeight、rightHeight会分别获取root的左右子树的高度int leftHeight = 0, rightHeight = 0;if (!_IsBalance(root->_left, leftHeight) || !_IsBalance(root->_right, rightHeight)){return false;}// 如果高度差的绝对值 >= 2,AVL树不平衡int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "不平衡" << endl;return false;}// 如果高度差 != root->_bf,AVL树插入过程中的平衡因子更新有问题if (diff != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}// 将root自己的高度通过引用返回给上一层栈帧height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;// root的左子树平衡、右子树平衡、root自身也平衡,那这棵AVL树就平衡return true;
}
参考文章
数据结构 —— 图解AVL树(平衡二叉树)
高度平衡二叉搜索树(AVLTree)
【数据结构】AVL树的删除(解析有点东西哦)
相关文章:

C++笔记:从零开始一步步手撕高阶数据结构AVL树
文章目录 高度平衡二叉搜索树实现一颗AVL树结点与树的描述——定义类AVL树的插入操作步骤1:按照二叉搜索树的方法插入结点步骤2:自底向上调整平衡因子步骤3:触发旋转操作(AVL树平衡的精髓)右单旋左单旋左右双旋右左双旋…...
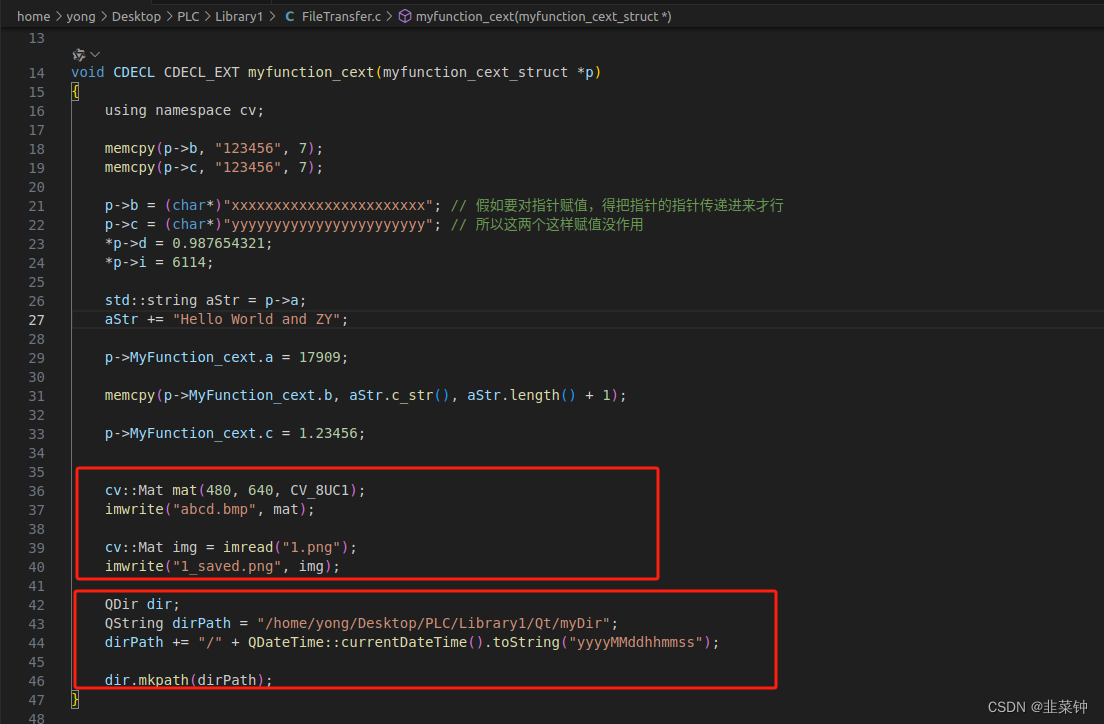
CodeSys通过C函数接口调用Qt
文章目录 1.背景介绍2.修改makefile2.1.将编译器由c改成c2.2.使能opencv库2.3.使能Qt库 3.在代码中使用Qt库函数 1.背景介绍 建议先查看之前的文章【CodeSys中调用C语言写的动态库】,了解如何创建一个能够被codesys调用的动态库。 假如想要在函数中使用Qt或者第三方…...

线性代数笔记18--行列式公式、代数余子式
1. 行列式公式推导 二阶行列式推导 [ a b c d ] [ a 0 c d ] [ 0 b c d ] [ a 0 0 d ] [ a 0 c 0 ] [ 0 b c 0 ] [ 0 b 0 d ] [ a 0 0 d ] − [ b 0 0 c ] a d − b c \begin{align} \begin{bmatrix} a & b \\ c & d \end{bmatrix}& \begin{bmatrix} a &…...

最新2024年项目基金撰写与技巧及GPT融合应用
随着社会经济发展和科技进步,基金项目对创新性的要求越来越高。申请人需要提出独特且有前瞻性的研究问题,具备突破性的科学思路和方法。因此,基金项目申请往往需要进行跨学科的技术融合。申请人需要与不同领域结合,形成多学科交叉…...

Java八股文(Element Plus)
Java八股文のElement Plus Element Plus Element Plus 什么是Element UI 和 Element Plus? Element UI 和 Element Plus 是基于 Vue.js 的一套非常受欢迎的开源 UI 组件库,用于快速构建具有现代化设计和丰富交互效果的前端界面。 Element UI 和 Element…...
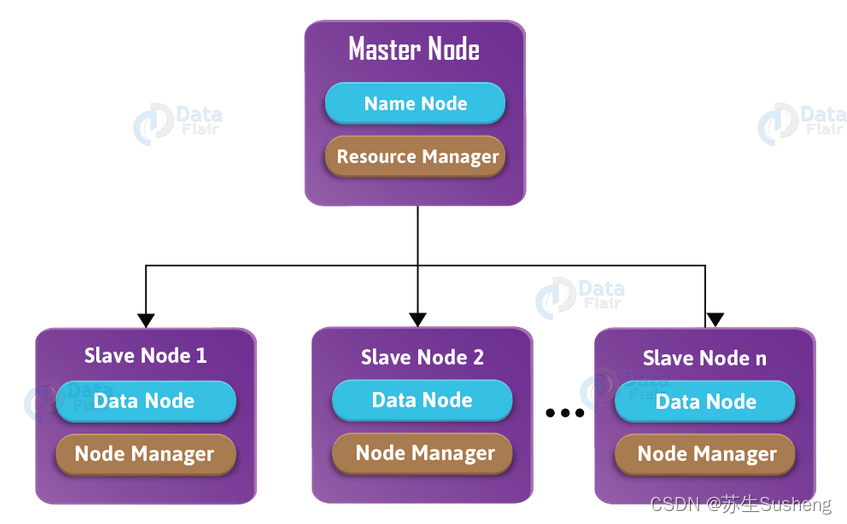
【Hadoop】Hadoop概述与核心组件
目录 Hadoop概述Hadoop 发展历史Hadoop 三大发行版本1.Apache Hadoop(常用)2.Cloudera Hadoop3.Hortonworks Hadoop优势优势总结——4高(高可靠、高扩展、高效、高容错) Hadoop组成1.HDFS管理者:NameNode(n…...
3D地图在BI大屏中的应用实践
前言 随着商业智能的不断发展,数据可视化已成为一项重要工具,有助于用户更好地理解数据和分析结果。其中,3D地图作为一种可视化工具,已经在BI大屏中得到了广泛地应用。 3D地图通过将地理信息与数据相结合,以更加直观…...

JavaScript 进阶(二)
一、深入对象 1.1创建对象三种方式 1. 利用对象字面量创建对象 2. 利用 new Object 创建对象 3.利用构造函数创建对象 1.2 构造函数 构造函数 : 是一种特殊的函数,主要用来初始化对象。 使用场景: 常规的 {...} 语法允许创建一个对象。…...

基于ssm+layui的图书管理系统
基于ssmlayui的图书管理系统 账户类型分为:管理员,用户管理员私有功能用户私有功能公共功能技术栈功能实现图 视频演示 账户类型分为:管理员,用户 图书管理系统主要登录账户类型为管理员账户与用户账户 管理员私有功能 账户管理…...
2024年最新阿里云和腾讯云云服务器价格租用对比
2024年阿里云服务器和腾讯云服务器价格战已经打响,阿里云服务器优惠61元一年起,腾讯云服务器61元一年,2核2G3M、2核4G、4核8G、4核16G、8核16G、16核32G、16核64G等配置价格对比,阿腾云atengyun.com整理阿里云和腾讯云服务器详细配…...

双指针算法_复写零
题目: 给一个固定长度的数组arr,将数组中出现的每一个0都复写一遍,并且将其余元素都往右移动 且不要再超过数组长度的位置写入元素,在数组上直接修改 示例: 双数组模拟操作: 从示例来看,因为…...

自习室预订系统|基于springboot框架+ Mysql+Java+B/S架构的自习室预订系统设计与实现(可运行源码+数据库+设计文档+部署说明)
推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 目录 前台功能效果图 学生功能模块 管理员功能登录前台功能效果图 系统功能设计 数据库E-R图设计 lunwen参…...
基于Java+SpringMVC+vue+element宠物管理系统设计实现
基于JavaSpringMVCvueelement宠物管理系统设计实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言 文末获取源…...

用miniconda建立PyTorch、Keras、TensorFlow三个环境
一、配置清华镜像conda源 由于网络问题,直接使用conda默认的源下载包可能会非常慢。为了解决这个问题,可以配置国内镜像源来加速包的下载。清华大学TUNA协会提供了一个常用的conda镜像源。下面是如何配置清华镜像源的步骤: 1. 配置清华conda…...
【QT 5 +Linux下qt软件点击.sh脚本运行+Dconf编辑器+学习他人文章+番外篇:点击脚本运行软件】
【QT 5 Linux下qt软件点击.sh脚本运行Dconf编辑器学习他人文章番外篇:点击脚本运行软件】 1、前言2、实验环境3、自我学习总结-本篇总结1、说明:代替qt的快捷方式2、适用性更广3、了解工具:Dconf编辑器注意事项: 4、参考链接-感谢…...

多模态大模型Claude 3正式接入集简云与语聚!对标GPT-4且支持中文
自OpenAI发布GPT-4以来,引发了业务模式与应用使用的巨大变革,掀起了各大企业对于多模态大模型的研究热潮。3月初,AnthropicClaude在官网正式发布Claude 3系列多模态大模型,据了解,该模型在多个维度上超越了GPT-4&#…...

.NET后端返回File文件,及前端处理直接在浏览器下载
后端代码 [AllowAnonymous] public System.Web.Mvc.ActionResult ExportByteExcel(string datatab, string columnnames, string schemecode) { 返回excel。 string ReportName "ExcelTemplete" DateTime.Now.Ticks.ToString(); …...

如何压缩图片文件大小?教大家几种方法
当图片文件较大时,图片压缩可以有效的缩小图片kb,从而使图片储存起来更加方便,也可以解决上传时图片大小被限制的问题,那么我们有什么方法可以简单快速的将图片大小压缩呢?下面就来给大家分享几个如何修改照片大小kb的…...

Qt 如何搭建Lua的运行环境
一、Lua简介 Lua 是一种强大的、高效的、轻量级的、可嵌入的脚本语言。它支持过程(procedural)编程、面向对象编程、函数式编程以及数据描述。Lua 是动态类型的,运行速度快,支持自动内存管理,因此被广泛用于配置、脚本…...
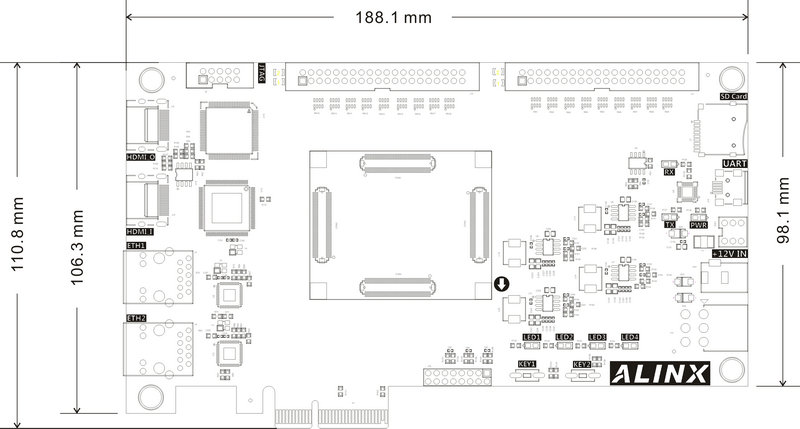
产品推荐 - ALINX XILINX FPGA开发板 Artix-7 XC7A100T-2FGG484I
01开发板介绍 此款开发板采用核心板扩展板的模式,方便用户对核心板的二次开发利用。FPGA使用的是Xilinx公司的ARTIX-7系列的芯片,型号为XC7A100T-2FGG484I。在核心板使用了2片MICRON公司的MT41J256M16HA-125 DDR3芯片,组合成32bit的数据总线…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
