【单目3D目标检测】MonoDDE论文精读与代码解析
文章目录
- Preface
- Pros and Cons
- Abstract
- Contributions
- Preliminary
- Direct depth estimation
- Depth from height
- Pespective-n-point(PnP)
- Pipeline
- Diverse Depth Estimations
- Robust Depth Combination
- Output distribution
- Selecting and combining reliable depths
- 3D Geometry Confidence
Preface
[CVPR2022] Li Z, Qu Z, Zhou Y, et al. Diversity Matters: Fully Exploiting Depth Clues for Reliable Monocular 3D Object Detection[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 2791-2800.
Paper
[Code] Coming soon… …
Pros and Cons
- 和MonoFlex很相似,都是在depth estimation上做的创新,相比于MonoFlex,MonoDDE额外利用了8个顶点坐标信息(又和MonoGround很像)
- 优点:集中了更多的深度假设和几何约束,并不局限于回归物体的中心深度
- 缺点:没有直接回归物体的3D坐标,并且代码未开源
Abstract
单幅图像深度估计是单目三维目标检测(M3OD)中最具挑战性的部分,是一个固有的不适定问题。许多现有的方法依赖于预先的假设来弥补单目图像中缺失的空间信息,并为每个感兴趣的物体预测唯一的深度值。然而,这些假设在实际应用中并不总是成立的。
为了解决这一问题,我们提出了一个深度求解系统,该系统充分探索了单目3D目标检测中子任务的视觉线索,并对每个目标的深度生成多个估计。由于深度估计在本质上依赖于不同的假设,它们呈现出不同的分布。即使一些假设崩溃了,建立在其余假设上的估计仍然是可靠的。
此外,我们还制定了深度选择和组合策略。该策略能够去除由崩溃假设引起的异常估计,并自适应地将剩余的估计组合成一个单一的估计。通过这种方式,我们的深度求解系统变得更加精确和健壮。在不引入任何额外信息的情况下,利用单目3D目标检测的多个子任务线索,在KITTI 3D物体检测基准测试中,我们的方法在中等水平的测试分割上,相对超过目前最好的方法20%以上,同时仍然保持实时效率。
Contributions
- 指出深度估计的多样性是单目三维目标检测的关键。相应地,开发了一种新的深度求解系统,每个目标可求解20个深度
- 1:direct depth estimation
- 3:depth from height
- 16:depth from 8 keypoints
- 设计了一种深度选择和合并策略,消除由崩溃假设引起的异常值,并将剩余的可靠估计合并到单个深度
- 此外,提出了一种新的条件三维置信度建模方法
Preliminary
Direct depth estimation
由backbone直接回归得到,之后根据投影模型得到物体的3D坐标:
x=(uc−cu)zfx,y=(vc−cv)zfy(1)x=\frac{\left(u_c-c_u\right) z}{f_x}, \quad y=\frac{\left(v_c-c_v\right) z}{f_y} \tag{1} x=fx(uc−cu)z,y=fy(vc−cv)z(1)
其中,(x,y)(x,y)(x,y)为物体的3D坐标,(fx,fy)(f_x,f_y)(fx,fy)为内参焦距,(cu,cv)(c_u,c_v)(cu,cv)为内参相机光轴与相机成像平面的交点在像素坐标系下的坐标,(uc,vc)(u_c,v_c)(uc,vc)为物体的像素坐标
Depth from height
与MonoFlex中的一致,分为三组,然后利用几何关系得到物体的depth:
z=fyhh′(2)z=\frac{f_yh}{h'} \tag{2} z=h′fyh(2)
其中,hhh是物体的实际高度,h′h'h′是物体的像素高度,分组示意图如下所示(b):

Pespective-n-point(PnP)
PnP(Perspective-n-Point)是求解3D点到2D点对运动的方法,目的是求解相机坐标系相对世界坐标系的位姿。它描述了已知n个3D点的坐标(相对世界坐标系)以及这些点的像素坐标时,如何估计相机的位姿(即求解世界坐标系到相机坐标系的旋转矩阵RRR和平移向量TTT)
符号说明:
- 世界坐标系的坐标:Po=(xo,yo,zo)T\mathbf{P}^o=\left(x^o, y^o, z^o\right)^TPo=(xo,yo,zo)T
- 相机坐标系的坐标:Pc=(xc,yc,zc)T\mathbf{P}^c=\left(x^c, y^c, z^c\right)^TPc=(xc,yc,zc)T
- 像素坐标系的坐标:[u,v,1]T[u, v, 1]^T[u,v,1]T
从世界坐标系到相机坐标系:
利用旋转矩阵和平移矩阵即可完成:
[xc,yc,zc]T=R[xo,yo,zo]T+T(3)\left[x^c, y^c, z^c\right]^T=\mathbf{R}\left[x^o, y^o, z^o\right]^T+\mathbf{T} \tag{3} [xc,yc,zc]T=R[xo,yo,zo]T+T(3)
其中,R\mathbf{R}R为旋转矩阵,T\mathbf{T}T为平移矩阵:
R=[cosθ0sinθ010−sinθ0cosθ],T=[x,y,z]T\mathbf{R}=\left[\begin{array}{ccc} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{array}\right], \quad \mathbf{T}=\left[\begin{array}{lll} x, & y, & z \end{array}\right]^T R=cosθ0−sinθ010sinθ0cosθ,T=[x,y,z]T
从相机坐标系到图像坐标系:
利用相机内参即可完成:
zc[u,v,1]T=K[xc,yc,zc]T(4)z^c[u, v, 1]^T=\mathbf{K}\left[x^c, y^c, z^c\right]^T \tag{4} zc[u,v,1]T=K[xc,yc,zc]T(4)
其中,K\mathbf{K}K为相机内参:
K=[fx0cu0fycv001]\mathbf{K}=\left[\begin{array}{ccc} f_x & 0 & c_u \\ 0 & f_y & c_v \\ 0 & 0 & 1 \end{array}\right] K=fx000fy0cucv1
核心点:
- 上述转换过程揭示了物体的关键点在世界坐标系与对应的像素坐标系之间的几何关系
- 这种几何关系中,Po\mathbf{P}^oPo是人为预定义的,K\mathbf{K}K是相机内参(已知的),R,(u,v)\mathbf{R},(u,v)R,(u,v)是由网络预测得到的,只有平移矩阵T\mathbf{T}T是需要求解的
- Since every 3D keypoint provides 2 geometric constraints, we can obtain x, y and z simultaneously using the least squares method if we have at least 2 keypoints
Pipeline

- Backbone:DLA34
- Head:多组回归头
- categorical heatmap
- 2D bounding box
- dimension
- keypoint offsets
- orientation
- depth
- multiple uncertainty items
- 之后经过深度选择机制,过滤掉深度异常值,并将剩余的深度值合并为一个值,然后代入公式(1),就可以计算得到物体的坐标信息
Diverse Depth Estimations
在MonoDDE中,作者期望开发的深度求解系统具有三个关键特征:
- 它应该专注于获得深度z,而不是同时计算x、y和z
- 与现有方法相比,它应该产生多种多样的深度估计值
- 它应充分利用所有可用信息,包括视觉线索、估计目标中心、维度、方向和关键点等
Robust Depth Combination
尽管作者设计的深度解决系统产生了多样化的深度表示,并且包括有希望的估计,但它们还包含异常值。因此,作者之后考虑的问题是如何选择更准确的估计并将它们组合成一个值。为此,设计了一种策略,迭代地去除异常值并根据不确定性合并剩余的深度值
Output distribution
假设预测输出的深度都满足高斯分布,在网络head中加一个分支,用于预测该分布的均值和方差,并使用以下损失进行学习:
Lσ=∣p−p∗∣σ+logσ(5)L_\sigma=\frac{\left|p-p^*\right|}{\sigma}+\log \sigma \tag{5} Lσ=σ∣p−p∗∣+logσ(5)
其中,p,σp,\sigmap,σ分别为输出分布的均值和标准差,p∗p^*p∗为GT值,σ\sigmaσ在整个过程中隐式学习,不需要GT值进行监督
然后,作者还定义了包含N个高斯分布变量si∼N(μi,σi2)s_i \sim \mathcal{N}\left(\mu_i, \sigma_i^2\right)si∼N(μi,σi2)的集合S={si}i=1NS=\left\{s_i\right\}_{i=1}^NS={si}i=1N的分布为新的高斯分布,因为所有的head都预测同一目标的深度,注意,这里的新高斯分布,其实是N个高斯分布的权重和,权重{ωi}i=1N\left\{\omega_i\right\}_{i=1}^N{ωi}i=1N表示如下:
ωi=1/σi2∑j=1N1/σj2(6)\omega_i=\frac{1 / \sigma_i^2}{\sum_{j=1}^N 1 / \sigma_j^2} \tag{6} ωi=∑j=1N1/σj21/σi2(6)
因此,集合SSS的均值(最终会被直接当成深度预测结果)和方差计算如下:
μs=∑i=1Nωiμi,σs2=∑i=1Nωi2σi2(7)\mu_s=\sum_{i=1}^N \omega_i \mu_i, \sigma_s^2=\sum_{i=1}^N \omega_i^2 \sigma_i^2 \tag{7} μs=i=1∑Nωiμi,σs2=i=1∑Nωi2σi2(7)
Selecting and combining reliable depths
作者首先使用公式(5)训练网络来预测20个深度分布的均值和方差,并将这20个分布组成集合S,然后基于3σ规则过滤掉离群值,并设计出类似于期望最大化(EM)算法的鲁棒算法:

- 首先将SSS初始化为空集,并将方差最小的深度放到SSS中
- 在maximization步骤中,μs\mu_sμs和σs2\sigma^2_sσs2使用公式(6)-(7)进行更新
- 在expectation步骤中,落入(μs−3σs,μs+3σs)\left(\mu_s-3 \sigma_s, \mu_s+3 \sigma_s\right)(μs−3σs,μs+3σs)的深度被添加到SSS
- 我们重复上述两个步骤,直到μs\mu_sμs和σs2\sigma^2_sσs2收敛
- 之后,将(μs−3σs,μs+3σs)\left(\mu_s-3 \sigma_s, \mu_s+3 \sigma_s\right)(μs−3σs,μs+3σs)的所有深度视为异常值,并将其去除
- 最终,可靠的depth就包含在SSS中,直接使用最终的μs\mu_sμs作为后续操作的组合深度zcz_czc
3D Geometry Confidence
Coming soon…
相关文章:

【单目3D目标检测】MonoDDE论文精读与代码解析
文章目录PrefacePros and ConsAbstractContributionsPreliminaryDirect depth estimationDepth from heightPespective-n-point(PnP)PipelineDiverse Depth EstimationsRobust Depth CombinationOutput distributionSelecting and combining reliable de…...
复习 Kotlin 从小白到大牛 第二版 笔记要点
4.2.2 常量和只读变量 常量和只读变量一旦初始化就不能再被修改。在kotlin中,声明常量是在标识符的前面加上val或const val 关键字。 1. val 声明的是运行时变量,在运行时进行初始化 2.const val 声明的是编译时常量,在编译时初始化 val …...
X264简介-Android使用(二)
X264简介-Android使用(二) 4、Ubuntu上安装ffmpeg: 检查更新本地软件包(如果未更新,reboot Vmware): sudo apt update sudo apt upgrade官网下载的source文件安装: http://ffmpe…...
)
【独家】华为OD机试 - 统计差异值大于相似值二元组个数(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明本期…...

掌握好Framework 才是王道~
现在面试对Android开发者的要求越来越高了!从最开始的阿里、头条、腾讯等大厂,到现在的互联网车企,面试总喜欢问道 Framework底层原理的相关问题 Android Framework的三大核心功能: 1、View.java:View工作原理,实现包…...
 A — C)
Codeforces Round 856 (Div. 2) A — C
Codeforces Round 856 (Div. 2) 文章目录A. Prefix and Suffix Array题目大意题目分析codeB. Not Dividing题目大意题目分析codeC. Scoring Subsequences题目大意题目分析codeA. Prefix and Suffix Array 题目大意 给出一个字符串所有的非空前后缀,判断原字符串是…...

2022年MathorCup数学建模B题无人仓的搬运机器人调度问题解题全过程文档加程序
2022年第十二届MathorCup高校数学建模 B题 无人仓的搬运机器人调度问题 原题再现 本题考虑在无人仓内的仓库管理问题之一,搬运机器人 AGV 的调度问题。更多的背景介绍请参看附件-背景介绍。对于无人仓来说,仓库的地图模型可以简化为图的数据结构。 仓库…...

开源项目的演进会遇到哪些“坑”?KubeVela 从发起到晋级 CNCF 孵化的全程回顾
作者:孙健波、曾庆国 点击查看:「开源人说」第五期《KubeVela:一场向应用交付标准的冲锋》 2023 年 2 月,**KubeVela [ 1] ** 经过全体 ToC 投票成功进入 CNCF Incubation,是云原生领域首个晋级孵化的面向应用的交付…...
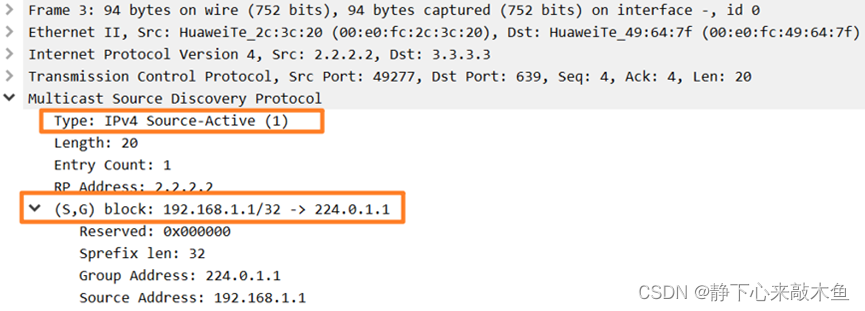
MSDP实验配置
目录 配置MSDP 配置PIM SM协议 配置各PIM SM域内的静态RP 配置MSDP对等体 配置域内的MSDP对等体 AR8和AR9建立EBGP邻居 配置域间的MSDP对等体 进行实验验证 什么是MSDP MSDP(Multicast Source Discovery Protocol)组播源发现协议的简称 用来传递…...

惊!初中生也来卷了……
大家好,我是良许。 前两天在抖音直播的时候,突然来了一位不速之客…… 他自称是初中生,一开始我还有点不太相信,直到跟他连麦,听到他还略带一些稚嫩的声音,我才知道,他没有骗我…… 他说他想学…...

kafka相关配置介绍
kafka默认配置 每个kafka broker中配置文件server.properties默认必须配置的属性如下: broker.id0 num.network.threads2 num.io.threads8 socket.send.buffer.bytes1048576 socket.receive.buffer.bytes1048576 socket.request.max.bytes104857600 log.dirs/tmp/…...
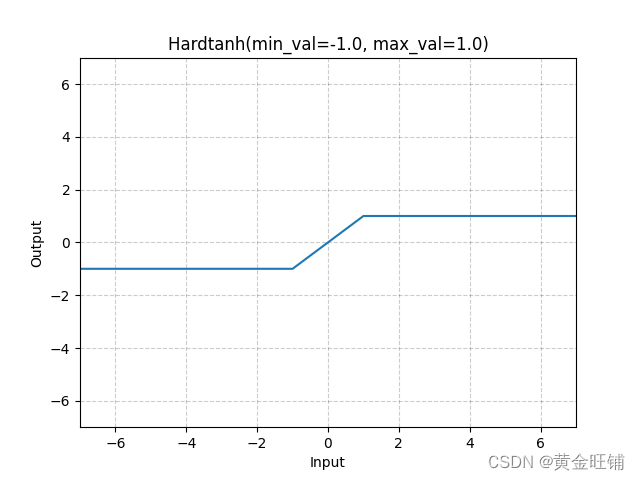
【PyTorch】教程:torch.nn.Hardtanh
torch.nn.Hardtanh 原型 CLASS torch.nn.Hardtanh(min_val- 1.0, max_val1.0, inplaceFalse, min_valueNone, max_valueNone) 参数 min_val ([float]) – 线性区域的最小值,默认为 -1max_val ([float]) – 线性区域的最大值,默认为 1inplace ([bool]) …...

神垕古镇景区5A级十年都没有实现的三大主因
钧 瓷 内 参 第40期(总第371期) 2023年3月5日 神垕古镇景区5A级十年都没有实现的三大主因 这是2013年,禹州市市政府第一次提出创建5A级景区到今年三月份整整十年啊! 目前神垕古镇景区是4A级景区,5A级一直进行中&a…...

react函数组件常用的几个钩子函数useState、useEffect、useRef、useCallback
react框架react框架包括包括两大类:类组件函数组件。类组件构成:constructor自定义方法。调用方法通过this.方法名()。constructor(superstate)构造器里面必有super字段。render()方法里面写页面布局。函数组件构成:各种钩子函数return()方法…...

4N60-ASEMI高压MOS管4N60
编辑-Z 4N60在TO-220封装里的静态漏极源导通电阻(RDS(ON))为2.5Ω,是一款N沟道高压MOS管。4N60的最大脉冲正向电流ISM为16A,零栅极电压漏极电流(IDSS)为1uA,其工作时耐温度范围为-55~150摄氏度。4N60功耗(…...
现代神经网络(VGG),并用VGG16进行实战CIFAR10分类
专栏:神经网络复现目录 本章介绍的是现代神经网络的结构和复现,包括深度卷积神经网络(AlexNet),VGG,NiN,GoogleNet,残差网络(ResNet),稠密连接网络…...
)
Java代码弱点与修复之——Dereference null return value(间接引用空返回值)
弱点描述 Dereference null return value,间接引用空返回值。是Coverity Scan静态代码分析工具中的一个警告,表示代码中有对可能为空(null)的方法或函数返回值进行间接引用(Dereference)操作。 该类型的漏洞可能会导致 NullPointerException 异常,并且会导致程序崩溃或…...

【冲刺蓝桥杯的最后30天】day3
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始更新备战蓝桥30天系列,一共30天,如果对你有帮助或者正在备…...

光伏发电嵌入式ARM工控机
随着智慧电力技术的不断发展和普及,越来越多的电力设备和系统需要采用先进的控制和监测技术来实现自动化管理和优化运行。其中,嵌入式 ARM 控制器技术在智慧电力领域中得到了广泛应用。同时,导轨安装也是该技术的重要应用场景之一。 导轨安装…...

推荐 7 个 Vue.js 插件,也许你的项目用的上(五)
当我们可以通过使用库轻松实现相同的结果时,为什么还要编写自定义功能?开发人员最好的朋友和救星就是这些第三方库。我相信一个好的项目会利用一些可用的最佳库。Vue.js 是创建用户界面的最佳 JavaScript 框架之一。这篇文章是关于 Vue.js 的优秀库系列的…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
