代码随想录 二叉树—填充每个节点的下一个右侧结点指针
今天没精力看了
题解c++:
class Solution {
public:Node* connect(Node* root) {if (root == NULL) return NULL; // 基本情况queue<Node*> q;q.push(root);while (!q.empty()) {int size = q.size();Node* prev = NULL;for (int i = 0; i < size; i++) {Node* node = q.front();q.pop();if (prev != NULL) {prev->next = node; // 连接上一个节点到当前节点}if (node->left) q.push(node->left);if (node->right) q.push(node->right);prev = node; // 更新上一个节点}// 重置上一个节点为NULL,以便下一层prev->next = NULL;}return root; // 返回根节点作为结果}
};
相关文章:

代码随想录 二叉树—填充每个节点的下一个右侧结点指针
今天没精力看了 题解c: class Solution { public:Node* connect(Node* root) {if (root NULL) return NULL; // 基本情况queue<Node*> q;q.push(root);while (!q.empty()) {int size q.size();Node* prev NULL;for (int i 0; i < size; i) {Node* no…...

用 bsdtar 做 Linux 全系统迁移 - 最省空间、最灵活的Linux系统迁移方式,但需要那么一点点技巧
(首发地址:学习日记 https://www.learndiary.com/2024/03/migrate-linux-with-bsdtar/ ) 我们在做 Linux 全系统迁移的时候,可以直接备份磁盘或分区(如 dd ),也可以备份全部文件(如…...
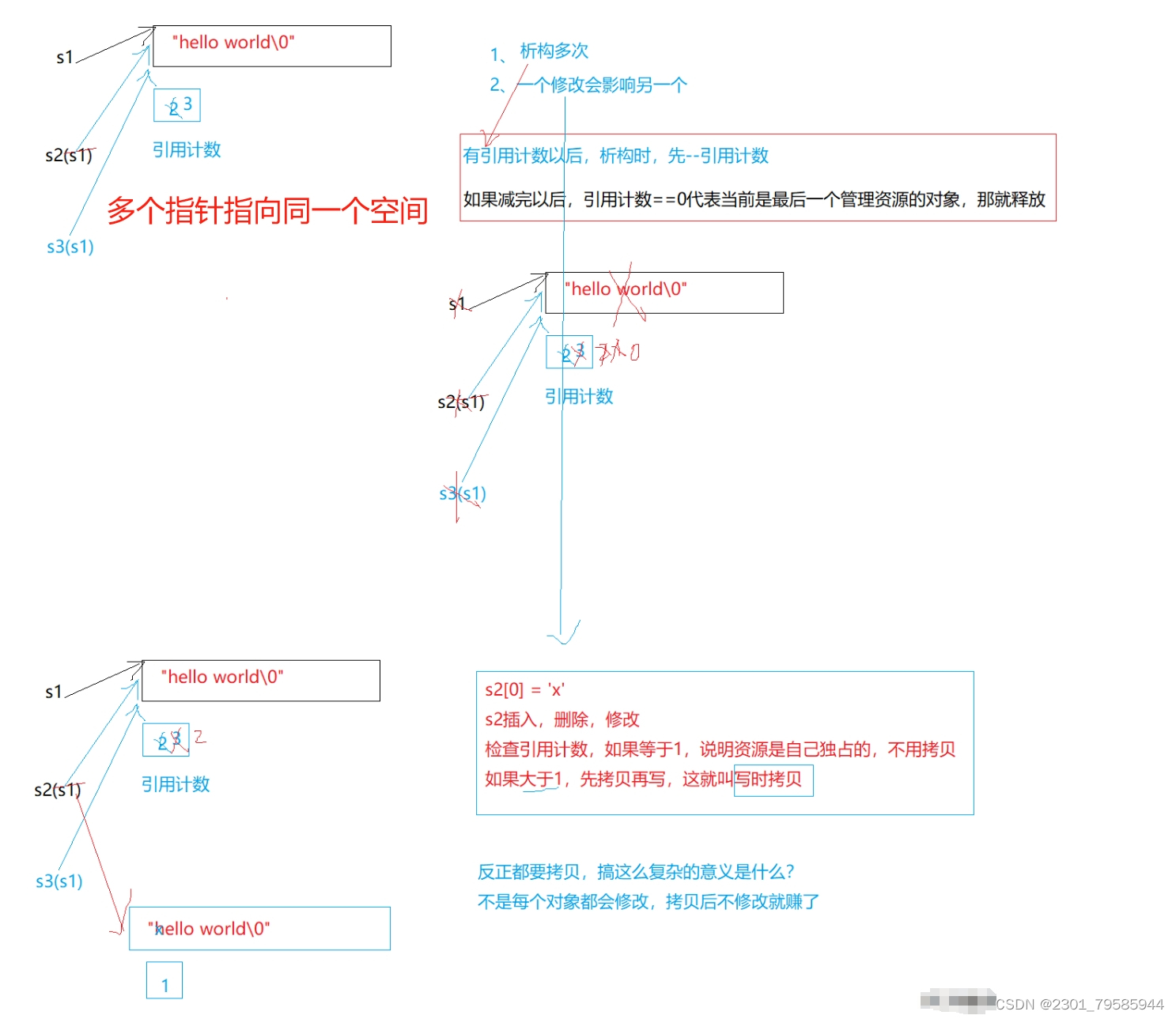
【模拟string函数的实现】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 模拟string函数的实现 浅拷贝 深拷贝 vs和g下string结构的说明 总结 前言 模拟string函数的实现 浅拷贝 深拷贝 总结 前言 世上有两种耀眼的光芒&#…...
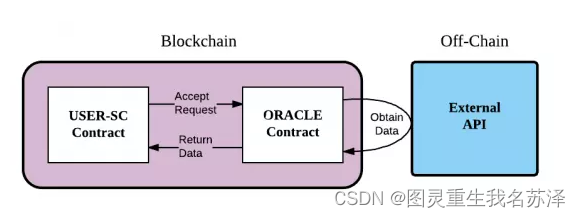
智能合约开发基础知识:最小信任机制、智能合约、EVM
苏泽 大家好 这里是苏泽 一个钟爱区块链技术的后端开发者 本篇专栏 ←持续记录本人自学两年走过无数弯路的智能合约学习笔记和经验总结 如果喜欢拜托三连支持~ 专栏的前面几篇详细了介绍了区块链的核心基础知识 有兴趣学习的小伙伴可以看看http://t.csdnimg.cn/fCD5E关于区块…...
程序人生——Java泛型和反射的使用建议
目录 引出泛型和反射建议93:Java的泛型是类型擦除的建议94:不能初始化泛型参数和数组建议95:强制声明泛型的实际类型 建议96:不同的场景使用不同的泛型通配符建议97:警惕泛型是不能协变和逆变的 建议98:建议…...

JavaSE-----认识异常【详解】
目录 一.异常的概念与体系结构: 1.1异常的概念: 1.2一些常见的异常: 1.3异常的体系结构: 1.4异常的分类: 二.异常的处理机制: 2.1 抛出异常: 2.2异常的捕获: 2.3try-catch-&…...
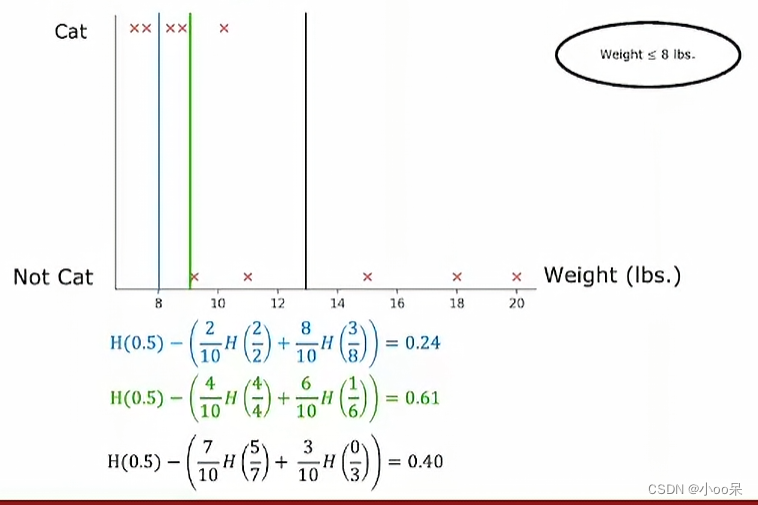
【机器学习300问】34、决策树对于数值型特征如果确定阈值?
还是用之前的猫狗二分类任务举例(这个例子出现在【机器学习300问】第33问中),我们新增一个数值型特征(体重),下表是数据集的详情。如果想了解更多决策树的知识可以看看我之前的两篇文章: 【机器…...

计算机二级(Python)真题讲解每日一题:《绘制雪花》
在横线处填写代码,完成如下功能…...

Rust 的 Arc<Mutex<T>> 的用法示例源代码
在 Rust 中,Arc<Mutex<T>> 是一种组合类型,它结合了 Arc(原子引用计数)和 Mutex(互斥锁)。Arc 用于在多个所有者之间共享数据,而 Mutex 用于确保在任意时刻只有一个线程可以访问被保…...

【NR 定位】3GPP NR Positioning 5G定位标准解读(十六)-UL-AoA 定位
前言 3GPP NR Positioning 5G定位标准:3GPP TS 38.305 V18 3GPP 标准网址:Directory Listing /ftp/ 【NR 定位】3GPP NR Positioning 5G定位标准解读(一)-CSDN博客 【NR 定位】3GPP NR Positioning 5G定位标准解读(…...

如何理解闭包
闭包是编程语言中一个重要的概念,特别是在函数式编程中常常会遇到。以下是对闭包的理解: 1. 定义: 闭包是一种函数,它引用了在其定义范围之外的自由变量(非全局变量),并且这些引用的变量在函数被调用时仍然保持活跃状态。2. 构成: 闭包通常由两部分组成:内部函数(函…...

python知识点总结(一)
这里写目录标题 一、什么是WSGI,uwsgi,uWSGI1、WSGI2、uWSGI3、uwsgi 二、python中为什么没有函数重载?三、Python中如何跨模块共享全局变量?四、内存泄露是什么?如何避免?五、谈谈lambda函数作用?六、写一个函数实现字符串反转,尽可能写出你知道的所…...
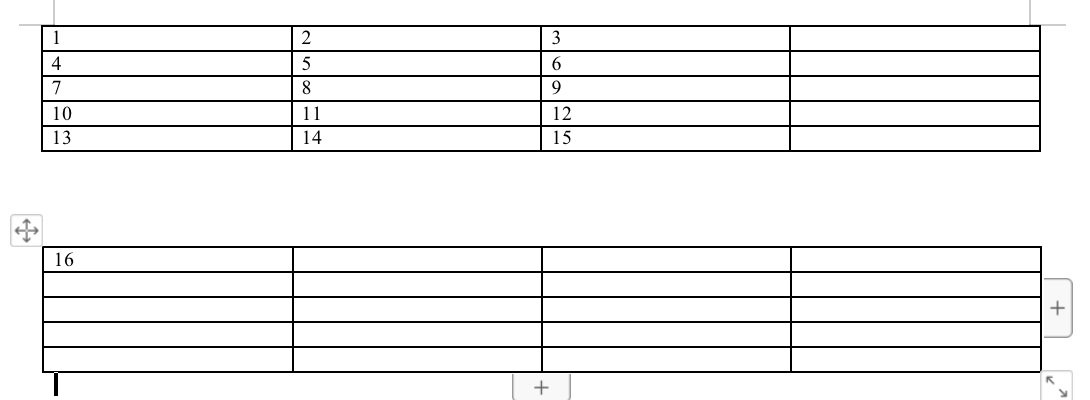
【Poi-tl Documentation】区块对标签显示隐藏改造
前置说明: <dependency><groupId>com.deepoove</groupId><artifactId>poi-tl</artifactId><version>1.12.1</version> </dependency>模板: 删除行表格测试.docx 改造前测试效果 package run.siyuan…...

第十四届蓝桥杯 三国游戏
一开始的思路就是想着暴力,但是呢,如果真的用暴力一个一个列的话,连30%的数据都搞定不了,所以这里需要考虑别的办法。 这道题的思路就是贪心。 我们这样想:既然要满足至少一个国X>YZ,那么我们何不变成…...
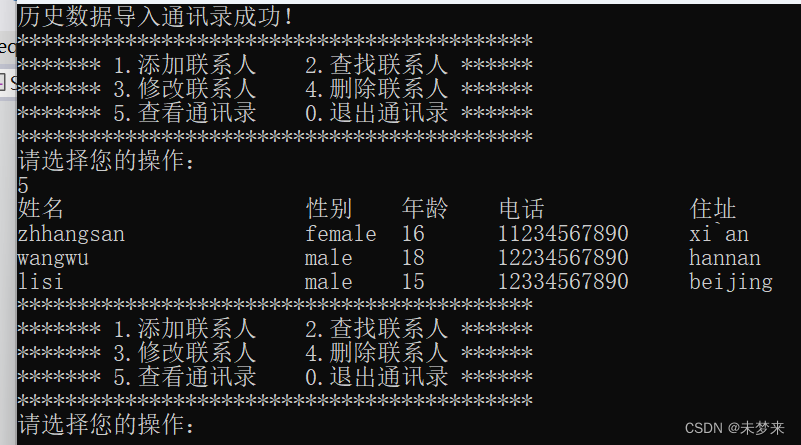
数据结构——通讯录项目
1.通讯录的介绍 顺序表是通讯录的底层结构。 通讯录是将顺序表的类型替换成结构体类型来储存用户数据,通过运用顺序表结构来实现的。 用户数据结构: typedef struct PersonInfo {char name[12];char sex[10];int age;char tel[11];char addr[100]; }…...
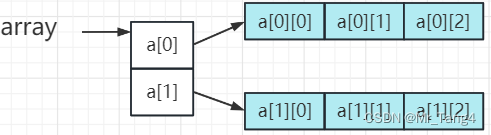
学点Java打小工_Day4_数组_冒泡排序
1 数组基本概念 程序算法数据结构 算法:解决程序的流程步骤 数据结构:将数据按照某种特定的结构来存储 设计良好的数据结构会导致良好的算法。 ArrayList、LinkedList 数组是最简单的数据结构。 数组:存放同一种类型数据的集合,在…...

内存分配方式?
内存分配方式主要有三种: 静态存储区分配:这种方式在程序编译的时候就已经分配好内存,并且这块内存在程序的整个运行期间都存在。全局变量和静态变量通常就是在静态存储区分配的。这种分配方式效率高,因为内存在程序开始执行前就已…...
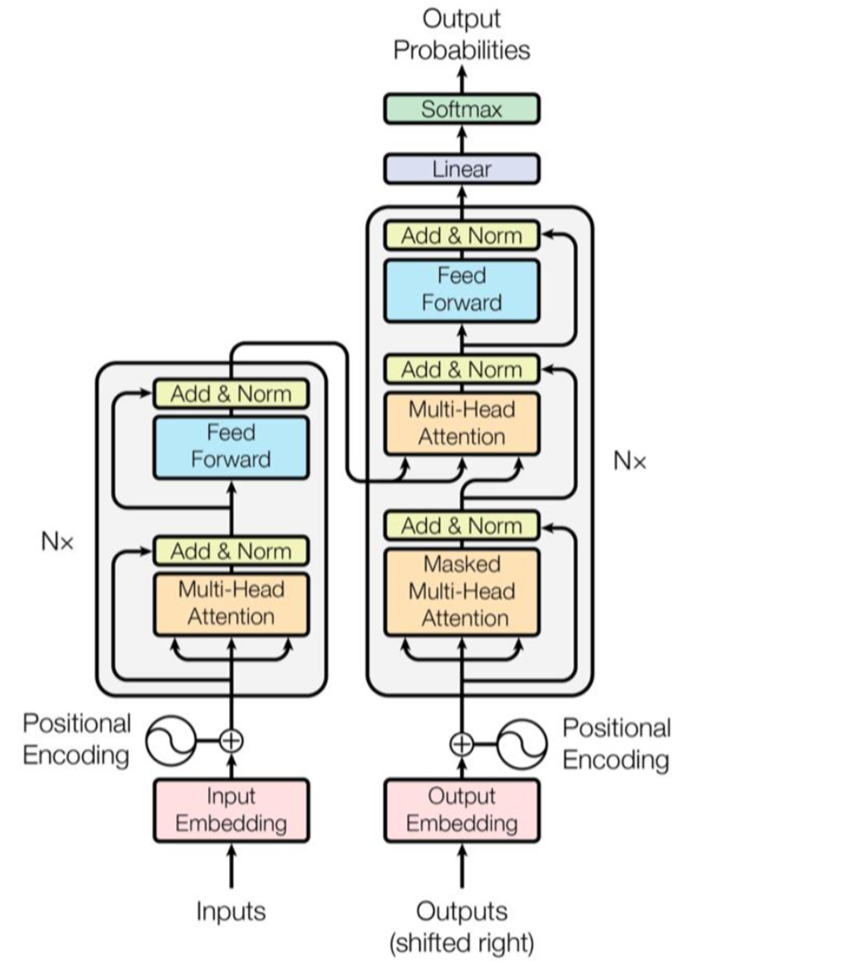
2024/3/17周报
文章目录 摘要Abstract文献阅读题目引言模型架构编码器和解码器堆栈AttentionPosition-wise Feed-Forward NetworksEmbeddings and SoftmaxPositional Encoding 实验数据实验结果 深度学习TransformerEncoderDecoder 总结 摘要 本周阅读了Transformer的开山之作《Attention Is…...

函数连续性和Lipschitz连续性
摘要: 直观上,Lipschitz连续性的含义是函数图像的变化速度有一个全局的上限,即函数的增长速率不会无限增加。这种性质确保了函数在任何地方都不会过于陡峭,有助于分析函数的行为,并且在优化、动力系统理论、机器学习等…...
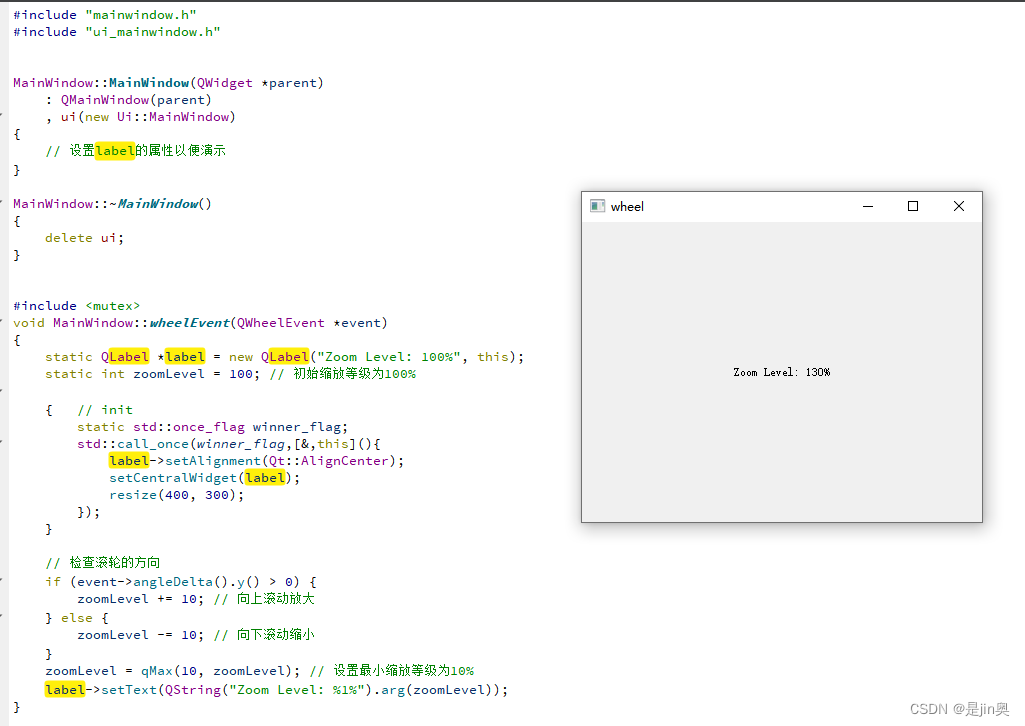
Qt 鼠标滚轮示例
1.声明 void wheelEvent(QWheelEvent *event) override;2.实现(方便复制、测试起见用静态变量) #include <mutex> void MainWindow::wheelEvent(QWheelEvent *event) {static QLabel *label new QLabel("Zoom Level: 100%", this);st…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
