C语言之快速排序
目录
一 简介
二 代码实现
快速排序基本原理:
C语言实现快速排序的核心函数:
三 时空复杂度
A.时间复杂度
B.空间复杂度
C.总结:
一 简介
快速排序是一种高效的、基于分治策略的比较排序算法,由英国计算机科学家C.A.R. Hoare在1960年提出。
二 代码实现
以下是使用C语言实现快速排序的基本步骤和代码示例:
快速排序基本原理:
- 选择一个基准元素(pivot),通常选择数组的第一个元素或者最后一个元素。
- 将所有比基准小的元素移动到基准元素之前,所有比基准大的元素移动到基准之后。这个操作被称为分区操作(partition)。
- 对基准左右两边的子数组分别递归地进行上述操作。
C语言实现快速排序的核心函数:
#include <stdio.h>// 分区操作,返回基准元素最后的位置
int partition(int arr[], int low, int high) {int pivot = arr[high]; // 基准元素(这里选取了数组的最后一个元素)int i = (low - 1); // 指针i初始化为low - 1for (int j = low; j <= high - 1; j++) {// 如果当前元素小于或等于基准元素,则与指针i所指向位置的元素交换,并将i后移一位if (arr[j] <= pivot) {i++;// 交换arr[i]和arr[j]int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}// 把基准元素放到正确的位置(即所有小于它的元素都在它前面)int temp = arr[i + 1];arr[i + 1] = arr[high];arr[high] = temp;return (i + 1);
}// 快速排序主函数
void quickSort(int arr[], int low, int high) {if (low < high) {// pi是基准元素最后所在的位置int pi = partition(arr, low, high);// 对基准元素左侧子数组进行递归排序quickSort(arr, low, pi - 1);// 对基准元素右侧子数组进行递归排序quickSort(arr, pi + 1, high);}
}// 测试快速排序
int main() {int arr[] = {10, 7, 8, 9, 1, 5};int n = sizeof(arr)/sizeof(arr[0]);quickSort(arr, 0, n-1);printf("Sorted array: \n");for (int i=0; i<n; i++)printf("%d ", arr[i]);return 0;
}这段代码首先定义了一个partition函数,该函数负责对输入数组进行一次划分操作,然后通过quickSort函数递归地对左右两个子数组执行同样的操作,直到子数组只剩下一个元素为止(因为只有一个元素的数组被认为是有序的)。最终,整个数组会被排序完成。
三 时空复杂度
A.时间复杂度
-
平均情况:当每次划分都能将数组大致均分为两个子数组时,快速排序的平均时间复杂度为
。这是由于每次递归调用都会将问题规模减半,并且需要对 n 个元素进行
层递归。
-
最好情况:最好的情况即每次选取的基准都能将数组完美地划分为大小相等的两部分,此时时间复杂度也是
。
-
最坏情况:最坏的情况是每次划分后,一个子数组为空或只有一个元素,而另一个子数组包含所有剩余元素。例如,对于已经完全有序的数组,这种情况会导致退化为
的时间复杂度。然而,在实际应用中,可以通过随机化选择基准元素(如三数取中法)来避免这种极端情况的发生,从而保证快速排序在期望下的时间复杂度仍为
。
B.空间复杂度
-
递归栈空间:快速排序是一种递归算法,其递归深度取决于输入数据的结构。在最坏情况下,递归深度可以达到 n,所以空间复杂度为 O(n)。但大多数情况下,递归深度为
,此时的空间复杂度主要来自于递归调用栈,约为
。
-
辅助空间:快速排序在原地排序的情况下不需要额外的数据存储空间,除了递归调用栈所占用的空间外,算法本身不使用其他额外空间,因此辅助空间复杂度可认为是 O(1)。
C.总结:
综上所述,快速排序在理想情况下是一个非常高效的排序算法,具有较好的平均性能。不过需要注意的是,为了避免最坏情况下的性能下降,通常会采取一些策略优化基准元素的选择方法。
相关文章:
C语言之快速排序
目录 一 简介 二 代码实现 快速排序基本原理: C语言实现快速排序的核心函数: 三 时空复杂度 A.时间复杂度 B.空间复杂度 C.总结: 一 简介 快速排序是一种高效的、基于分治策略的比较排序算法,由英国计算机科学家C.A.R. H…...
获取扇区航班数
1、Spark Streaming清洗服务,接收kafka中Topic为“task_ATC”中的数据,保存在MySQL中。 打开SpringBoot项目BigData-Etl-KongGuan 请认真阅读:在前面的“使用Spark清洗统计业务数据并保存到数据库中”任务阶段中应该已经完成了所有Topic的数…...

【已解决】npm install卡主不动的情况
使用 npm install 初始化前端项目时,会出现卡住不动的情况。原因是淘宝镜像源由原来的https://registry.npm.taobao.org 更换为下面这个: https://registry.npmmirror.com 直接在终端执行下面的指令即可: npm config set registry https://re…...
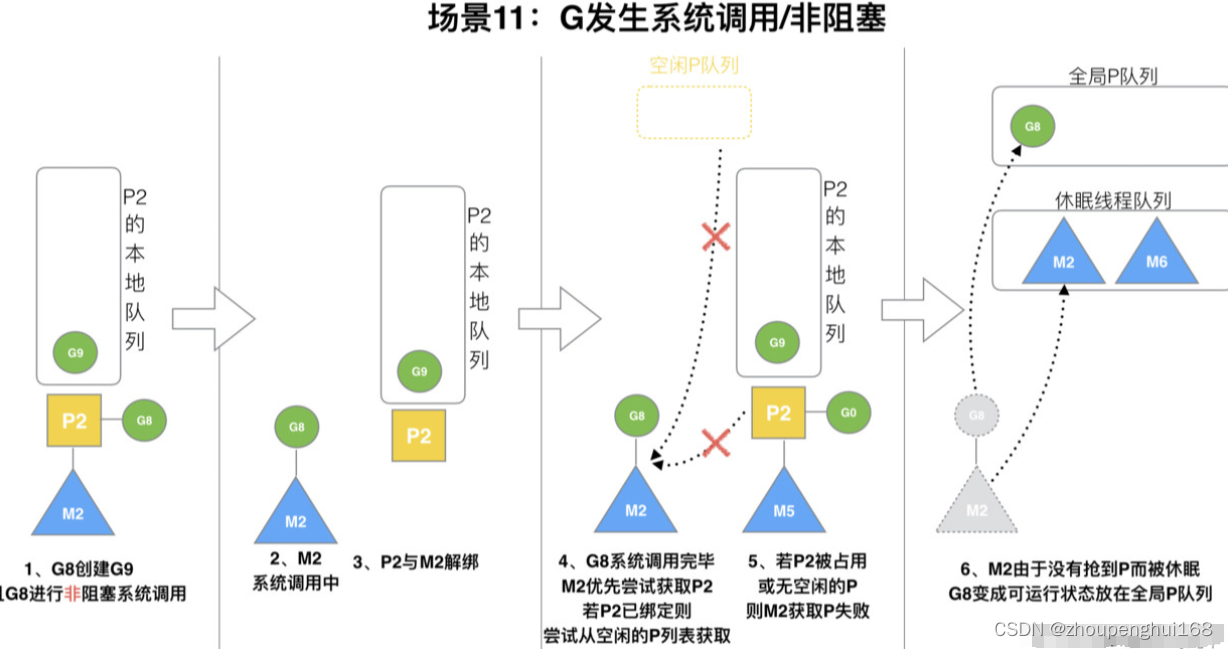
Golang协程详解
一.协程的引入 1.通过案例文章引入并发,协程概念 见:[go学习笔记.第十四章.协程和管道] 1.协程的引入,调度模型,协程资源竞争问题 通过上面文章可以总结出Go并发编程原理: 在一个处理进程中通过关键字 go 启用多个协程,然后在不同的协程中完成不同的子任…...
git:码云仓库提交以及Spring项目创建
git:码云仓库提交 1 前言 码云访问稳定性优于github,首先准备好码云的账户: 官网下载GIT,打开git bash: 查看当前用户的所有GIT仓库,需要查看全局的配置信息,使用如下命令: git …...

【Miniconda】基于conda避免运行多个PyTorch项目时发生版本冲突
【Miniconda】基于conda避免运行多个PyTorch项目时发生版本冲突 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程👈 希望得到…...

【机器学习-02】矩阵基础运算---numpy操作
在机器学习-01中,我们介绍了关于机器学习的一般建模流程,并且在基本没有数学公式和代码的情况下,简单介绍了关于线性回归的一般实现形式。不过这只是在初学阶段、为了不增加基础概念理解难度所采取的方法,但所有的技术最终都是为了…...

《A Second-Order PHD Filter With Mean and Variance in Target Number》学习心得
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. 主要内容2. PHD、CPHD和SO-PHD之间的差别2.1 PHD2.2 CPHD2.3 SO-PHD2.4 关于“CPHD对每个可能的目标数量状态进行建模”3. PHD、CPHD和SO-PHD描述目标数量分布所用的参数3.1 PHD所用参数3.2 CPH…...

React 实现下拉刷新效果
简介 本文基于react实现下拉刷新效果,在下拉的时候会进入loading状态。 实现效果 效果如上图所示,在下拉到底部时候,会出现loading条,在处理完成后loading条消失。 具体代码 布局 & 逻辑 import {useRef, useState} from …...

使用endnote插入引用文献导致word英文和数字变成符号的解决方案
使用endnote插入引用文献导致word英文和数字变成符号的解决方案 如图使用endnote插入引用文献导致word英文和数字变成符号字体Wingdings Wingdings 是一个符号字体系列,它将许多字母渲染成各式各样的符号,用途十分广泛。 解决方法: 直接通过更…...

npm下载慢换国内镜像地址
1 设置淘宝镜像地址 npm config set registry http://registry.npm.taobao.org 2 查看当前下载地址 npm config get registry 3 其它镜像地址列表: 1. 官方镜像:https://registry.npmjs.org/ 2. 淘宝镜像:https://registry.npm.taobao.o…...
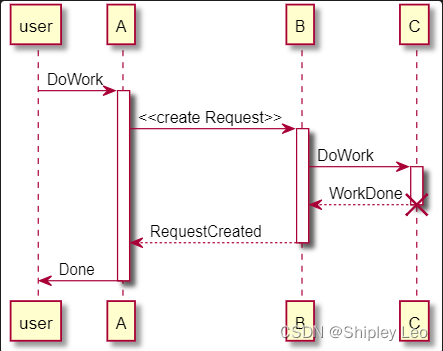
开源绘图工具 PlantUML 入门教程(常用于画类图、用例图、时序图等)
文章目录 一、类图二、用例图三、时序图 一、类图 类的UML图示 startuml skinparam classAttributeIconSize 0 class Dummy {-field1 : String#field2 : int~method1() : Stringmethod2() : void } enduml定义能见度(可访问性) startumlclass Dummy {-f…...
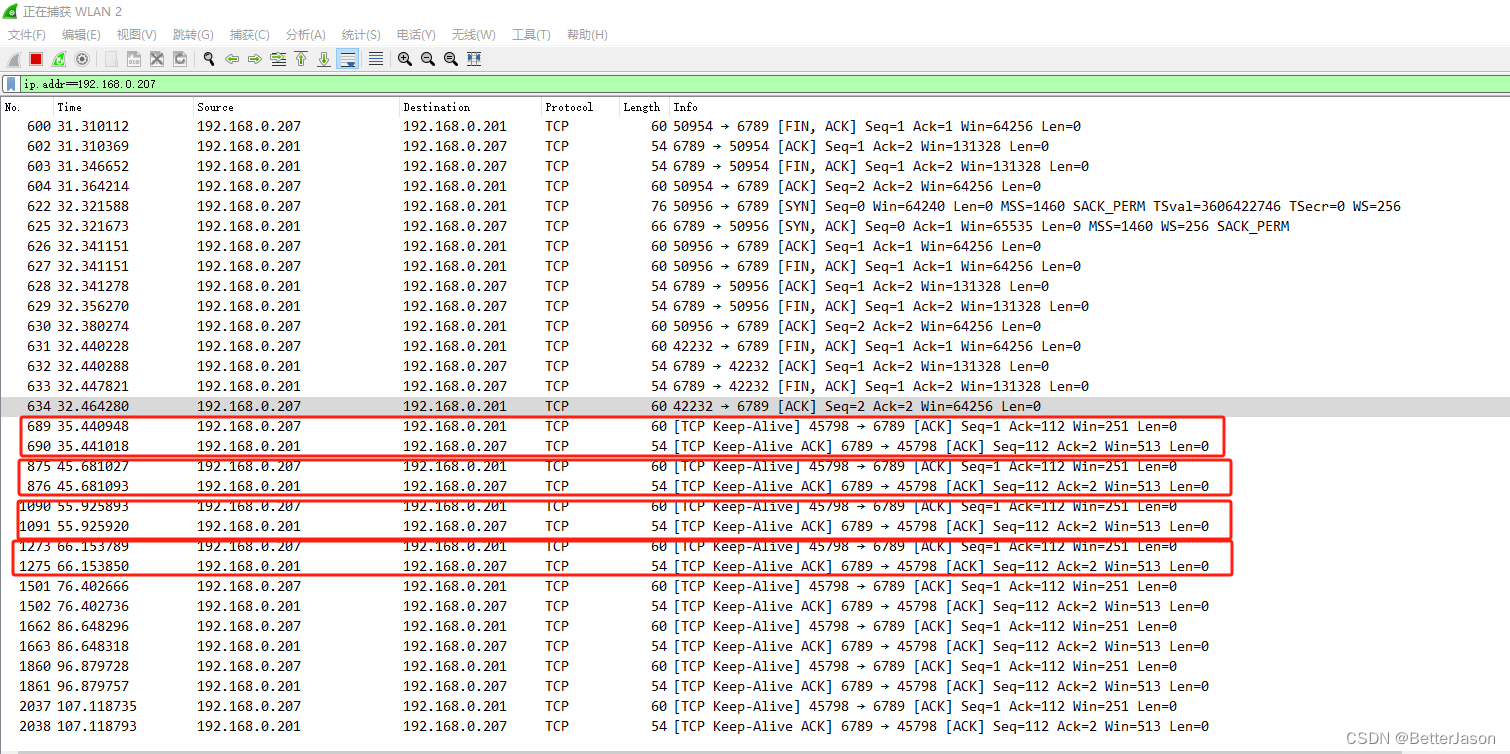
Ubuntu20下C/C++编程开启TCP KeepAlive
1、在linux下,测试tcp保活,可以使用tcp自带keepalive功能。 2、几个重要参数: tcp_keepalive_time:对端在指定时间内没有数据传输,则向对端发送一个keepalive packet,单位:秒 tcp_keep…...
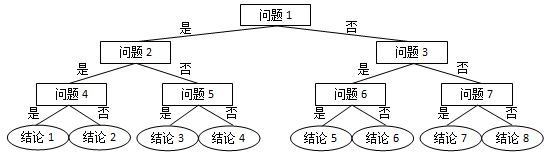
前世档案(不用二叉树语法秒杀版c++)
网络世界中时常会遇到这类滑稽的算命小程序,实现原理很简单,随便设计几个问题,根据玩家对每个问题的回答选择一条判断树中的路径(如下图所示),结论就是路径终点对应的那个结点。 现在我们把结论从左到右顺序…...
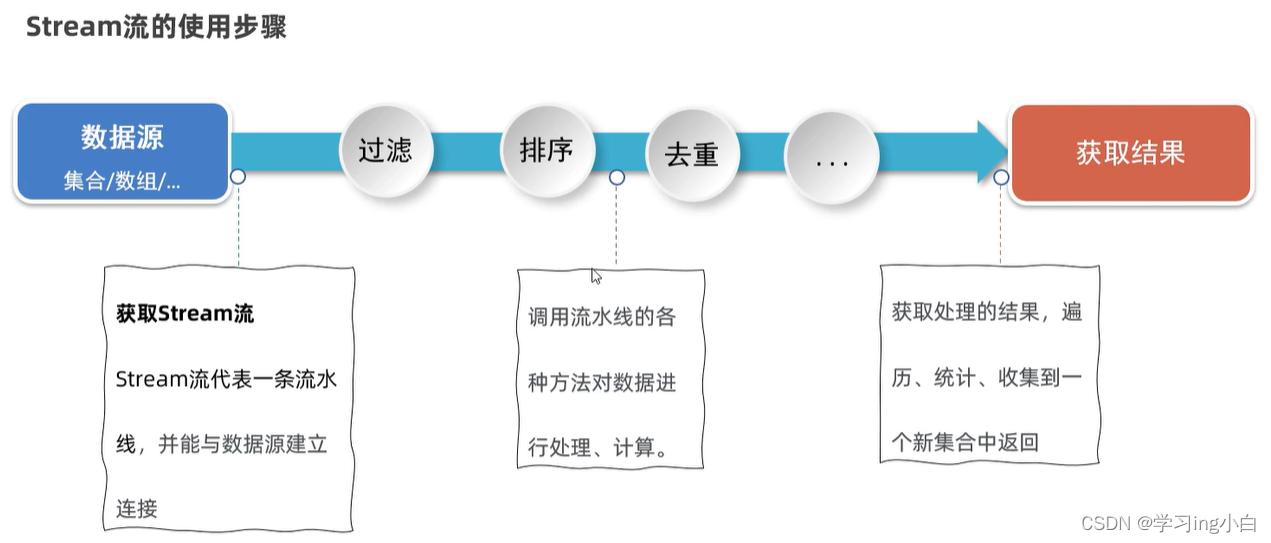
Java基础 - 9 - 集合进阶(二)
一. Collection的其他相关知识 1.1 可变参数 可变参数就是一种特殊形参,定义在方法、构造器的形参列表里,格式是:数据类型…参数名称; 可变参数的特点和好处 特点:可以不传数据给它;可以传一个或者同时传多个数据给…...
javaEE——线程的等待和结束
文章目录 Thread 类及常见方法启动一个线程中断一个线程变量型中断调用 interrupt() 方法来通知观察标志位是否被清除 等待一个线程获取当前线程引用休眠当前线程 线程的状态观察线程的所有状态观察 1: 关注 NEW 、 RUNNABLE 、 TERMINATED 状态的切换 多线程带来的风险为什么会…...

sqlplus设置提示符
作为DBA,需要管理好多数据库,经常会有一台服务器安装多个oracle实例的情况,为避免误操作实例,我们需要在执行sqkplus前,先通过$ echo $ORACLE_SID或 SQL>select name from v$database查看当前实例,这样难…...
macbook删除软件只需几次点击即可彻底完成?macbook删除软件没有叉 苹果笔记本MacBook电脑怎么卸载软件? cleanmymac x怎么卸载
在MacBook的使用过程中,软件安装和卸载是我们经常需要进行的操作。然而,不少用户在尝试删除不再需要的软件时,常常发现这个过程既复杂又耗时。尽管MacOS提供了一些基本的macbook删除软件方法,但很多时候这些方法并不能彻底卸载软件…...

Unity WebGL ios 跳转URL
需求: WebGL跳转网址 现象: Application.OpenURL("https://www.baidu.com"); 这个函数在安卓上可以用,IOS 不管用 解决方案: 编写js插件,unity调用js函数,由js跳转网址 注意事项 : 插件后缀为.jsli…...

机器学习模型—XGBoost
机器学习模型—XGBoost XGBoost(Extreme Gradient Boosting)是由陈天奇等人于2014年提出的一个高效可扩展的梯度提升库。它在梯度提升框架的基础上进行了优化和改进,被广泛应用于机器学习竞赛和实际应用中 作为GBDT(Gradient Boosting Decision Tree)的扩展版本,XGBoost在算…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
