电脑文件误删除如何恢复?分享三个简单数据恢复方法
在日常使用电脑的过程中,文件误删除的情况时有发生。无论是由于操作失误还是病毒感染,丢失的文件都可能对我们的工作和学习造成极大的影响。因此,掌握文件恢复的方法显得尤为重要。下面围绕“电脑文件误删除如何恢复”这一主题,给大家分享三种恢复方法。

一、回收站恢复法
当文件被误删除时,首先要检查的是电脑的回收站。Windows系统的回收站是一个临时存放已删除文件的地方,用户可以从中找回误删的文件。具体操作步骤如下:
1、打开回收站,查找被误删的文件。文件通常按照删除时间排序,因此可以根据大致的删除时间进行查找。

2、找到目标文件后,右键点击该文件,选择“还原”选项。文件将被恢复到原来的位置。
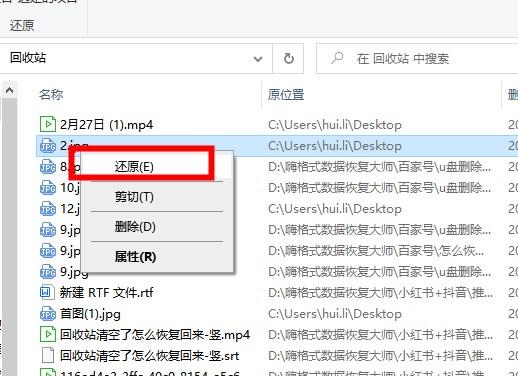
需要注意的是,如果回收站中的文件被清空或者文件过大而无法放入回收站,这种方法可能无法找回文件。此时,我们可以尝试使用专业的数据恢复软件。
二、嗨格式数据恢复大师法
【嗨格式数据恢复大师】是一款功能强大的数据恢复软件,能够支持多种文件格式的恢复,包括文档、图片、音频、视频等。其操作简便,恢复#热点引擎计划#成功率较高。下面是使用嗨格式数据恢复大师恢复文件的步骤:
1、下载并安装嗨格式数据恢复大师软件。确保从官方网站或可信渠道下载,以避免安装恶意软件。
2、打开软件,选择需要的恢复模式,如“误删除恢复”,点击文件丢失的位置进行扫描恢复。
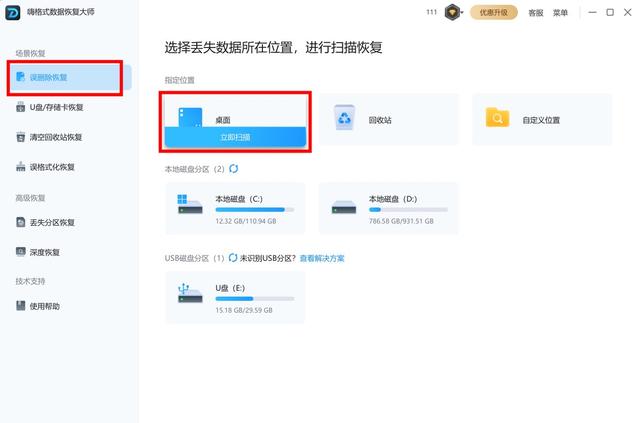
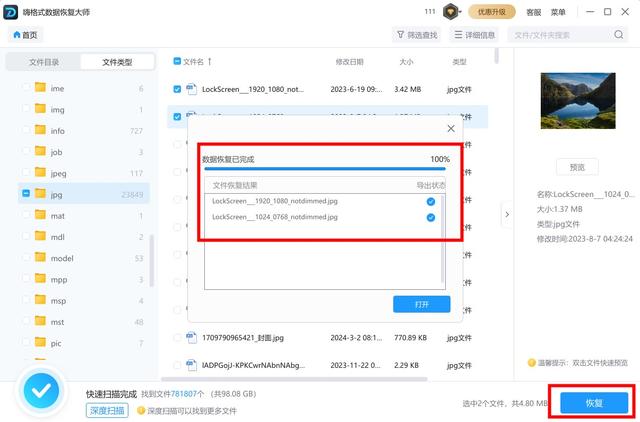
3、软件将扫描指定位置的硬盘,扫描完成后,在扫描结果中查找并勾选需要恢复的文件。
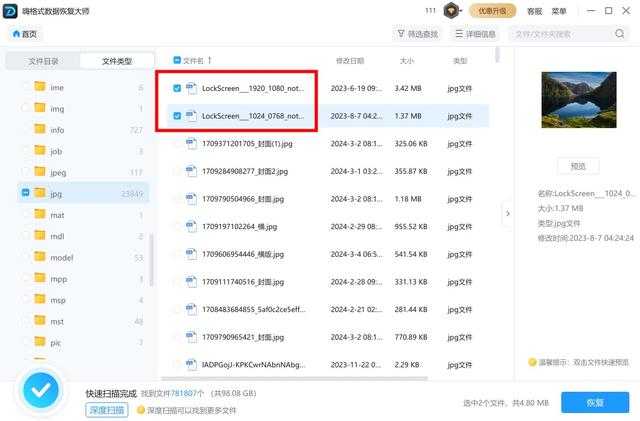
4、点击“恢复”按钮,等选择的数据文件恢复完成就可以了。
三、系统还原法
如果文件误删除发生在不久之前,并且系统设置了还原点,那么可以尝试使用系统还原法来恢复文件。系统还原可以将系统状态恢复到之前设置的还原点,包括文件、设置等。具体操作步骤如下:
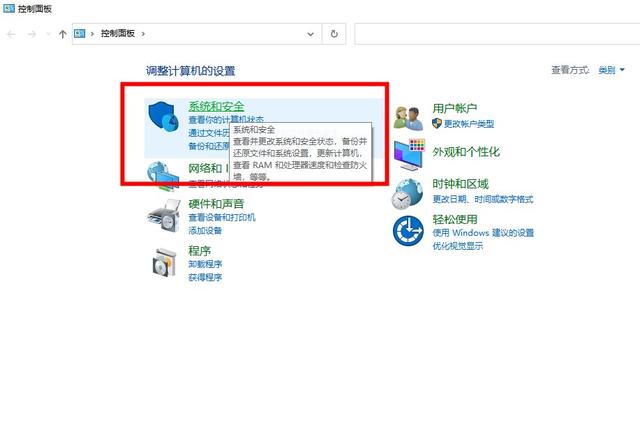
1、打开“控制面板”,找到“系统和安全”选项。
2、在“系统和安全”中,选择“系统”。
3、在左侧导航栏中,点击“系统保护”。
4、点击“系统还原”按钮,按照提示选择一个合适的还原点进行还原。
需要注意的是,系统还原将恢复整个系统的状态,而不仅仅是单个文件。因此,在使用此方法之前,请确保了解还原点的设置和可能带来的影响。
电脑文件误删除如何恢复?综上所述,当电脑文件误删除时,我们可以通过回收站恢复法、使用嗨格式数据恢复大师以及系统还原法来尝试恢复文件。每种方法都有其适用场景和注意事项,用户可以根据实际情况选择合适的方法进行操作。同时,为了避免文件丢失带来的损失,建议定期备份重要文件,并谨慎操作电脑。
相关文章:

电脑文件误删除如何恢复?分享三个简单数据恢复方法
在日常使用电脑的过程中,文件误删除的情况时有发生。无论是由于操作失误还是病毒感染,丢失的文件都可能对我们的工作和学习造成极大的影响。因此,掌握文件恢复的方法显得尤为重要。下面围绕“电脑文件误删除如何恢复”这一主题,给…...

MySQL实战:监控
监控指标 性能类指标 名称说明QPS数据库每秒处理的请求数量TPS数据库每秒处理的事务数量并发数数据库实例当前并行处理的会话数量连接数连接到数据库会话的数量缓存命中率Innodb的缓存命中率 功能类指标 名称说明可用性数据库是否正常对外提供服务阻塞当前是否有阻塞的会话…...

MySQL自增主键自动生成的主键重置
需求描述: 从主键1开始,insert操作自增了五个,库里五条数主键是1、2、3、4、5; 然后把主键是3、4、5的三条数据给删了,再继续insert,主键就是6了 因为这里表会把最大的数即5记住,下次自增即为…...

reverse_iterator实现
对于实现reverse_iterator,我们可以学栈和队列的实现过程,利用适配器,实现如下; #pragma oncetemplate<class Iterator,class Ref,class Ptr> class reverse_Iterator { public://构造函数:reverse_Iterator(Iterator it):…...

C++:什么情况下函数应该声明为纯虚函数
在C中,函数应该在以下情况下声明为纯虚函数: 抽象基类:当你希望定义一个基类,该基类不能被实例化,只能作为其他类的基类时,你应该在基类中声明至少一个纯虚函数。这样的基类被称为抽象基类。纯虚函数通过在…...
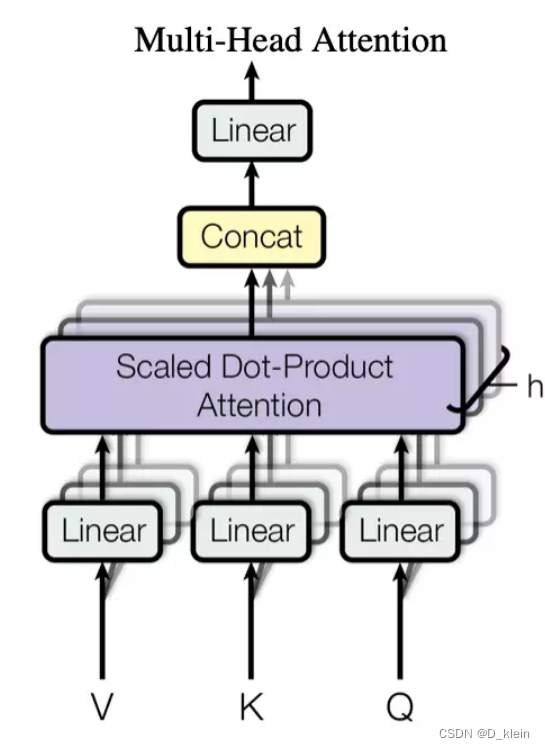
【全面了解自然语言处理三大特征提取器】RNN(LSTM)、transformer(注意力机制)、CNN
目录 一 、RNN1.RNN单个cell的结构2.RNN工作原理3.RNN优缺点 二、LSTM1.LSTM单个cell的结构2. LSTM工作原理 三、transformer1 Encoder(1)position encoding(2)multi-head-attention(3)add&norm 残差链…...
区块链推广海外市场怎么做,CloudNEO服务商免费为您定制个性化营销方案
随着区块链技术的不断发展和应用场景的扩大,区块链项目希望能够进入海外市场并取得成功已成为越来越多公司的目标之一。然而,要在海外市场推广区块链项目,需要采取有效的营销策略和措施。作为您的区块链项目营销服务商,CloudNEO将…...

【S5PV210】 | ARM的指令集合
【S5PV210】 | ARM的指令集合 时间:2024年3月17日23:32:06 目录 文章目录 【S5PV210】 | ARM的指令集合目录 ARM指令集具有一系列显著的特点。首先,它属于RISC(精简指令集计算机)架构,这意味着译码机制相对简单。在AR…...

2024-3-17Go语言入门
在Go语言中: var a chan int 定义了一个名为 a 的变量,其类型为 chan int。这意味着 a 是一个整型值的通道(channel)。通道是Go语言中用于goroutine之间通信的一种机制,你可以通过通道发送和接收特定类型的值。在这个例…...

AJAX-XMLHttpRequest
XMLHttpRequest 定义: XMLHttpRequest对象用于与服务器交互。通过XMLHttpRequest可以在不断刷新页面的情况下请求特定URL,获取数据。这允许网页在不影响用户操作的情况下,更新页面的局部内容。 关系: axios内部采用XMLHttpReques…...
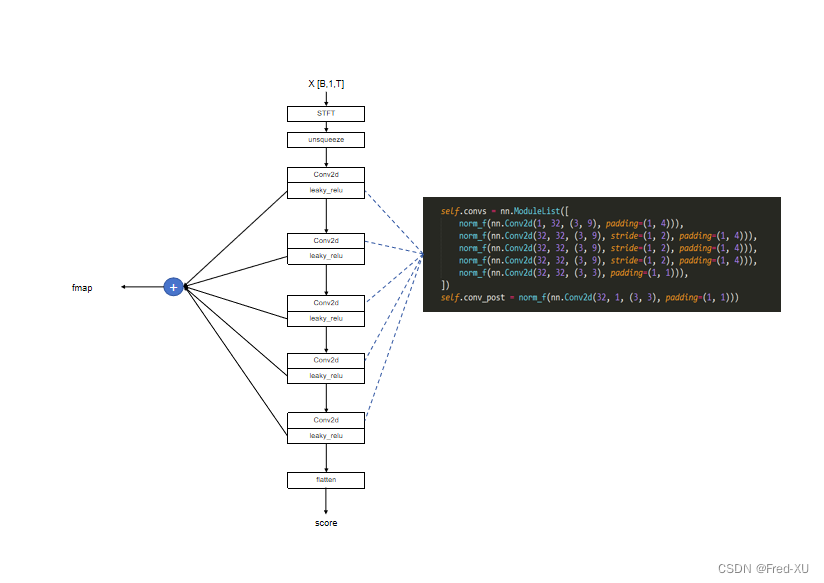
【GPT-SOVITS-04】SOVITS 模块-鉴别模型解析
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...

论文阅读_时序模型_iTransformer
1 2 3 4 5 6 7 8英文名称: ITRANSFORMER: INVERTED TRANSFORMERS ARE EFFECTIVE FOR TIME SERIES FORECASTING 中文名称: ITRANSFORMER:倒置Transformers在时间序列预测中的有效性 链接: https://openreview.net/forum?idX6ZmOsTYVs 代码: https://github.com/thum…...
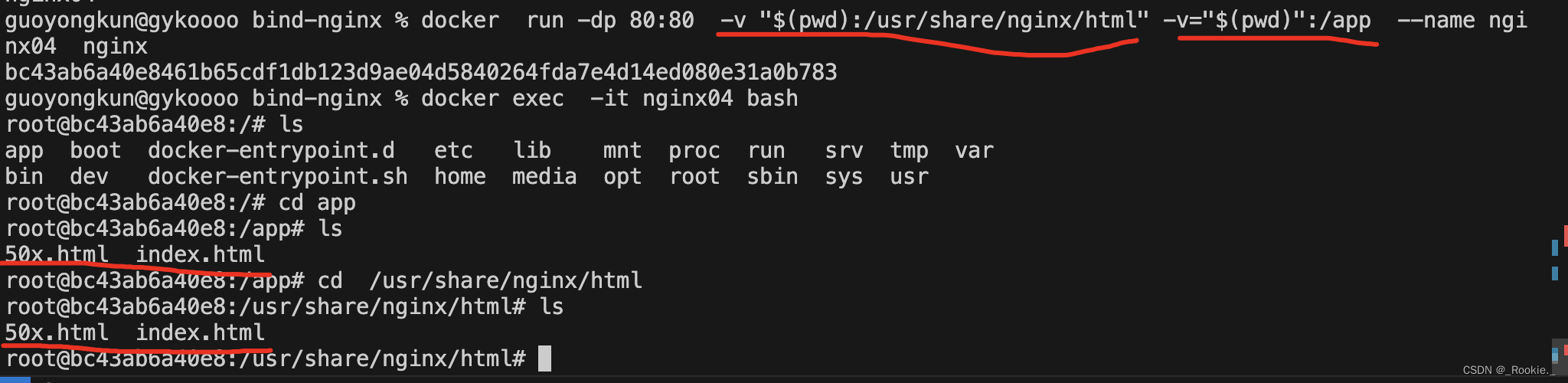
Docker 哲学 - 容器操作 -cp
1、拷贝 容器绑定的 volume的 数据,到指定目录 2、匿名挂载 volume 只定义一个数据咋在容器内的path,docker自动生成一个 sha256 的key作为 volume 名字。这个 sha256 跟 commitID 一致都是唯一的所以 ,docker利用这个机制,可以…...

作品展示ETL
1、ETL 作业定义、作业导入、控件拖拽、执行、监控、稽核、告警、报告导出、定时设定 欧洲某国电信系统数据割接作业定义中文页面(作业顶层,可切英文,按F1弹当前页面帮助) 涉及文件拆分、文件到mysql、库到库、数据清洗、数据转…...

python的集合应用
在Python中,集合是一种无序、可变的数据类型,用于存储不重复的元素。Python提供了内置的集合类型 set,以及 frozenset(不可变的集合)。以下是一些Python集合的常见应用场景: 去重: 集合是存储唯…...
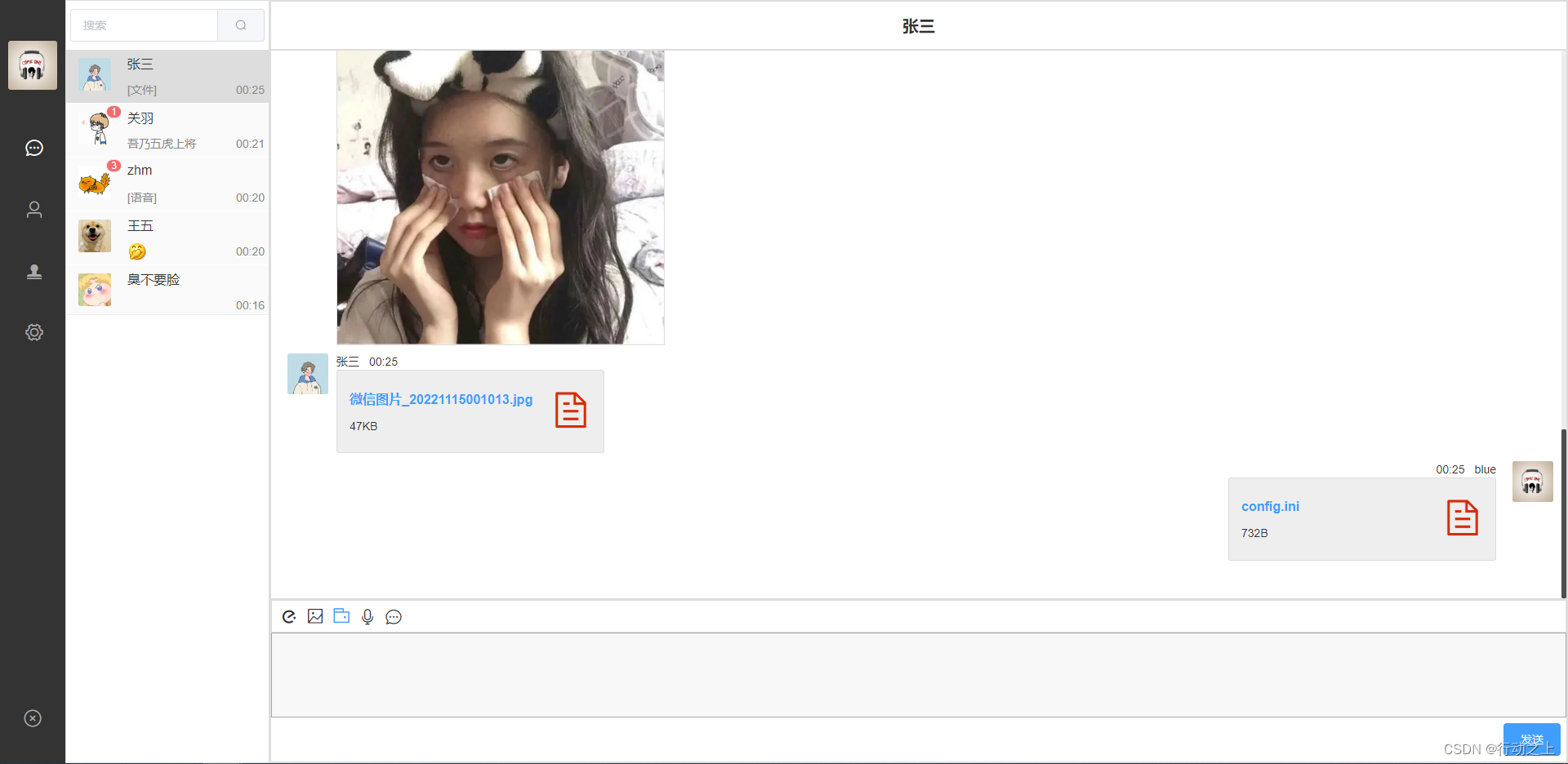
盒子IM开源仿微信聊天程序源码,可以商用
安装教程 1.安装运行环境 安装node:v14.16.0安装jdk:1.8安装maven:3.6.3安装mysql:5.7,密码分别为root/root,运行sql脚本(脚本在im-platfrom的resources/db目录)安装redis:5.0安装minio,命令端口使用9001,并创建一个名为”box-im”的bucket,…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Web)中篇
onBeforeUnload onBeforeUnload(callback: (event?: { url: string; message: string; result: JsResult }) > boolean) 刷新或关闭场景下,在即将离开当前页面时触发此回调。刷新或关闭当前页面应先通过点击等方式获取焦点,才会触发此回调。 参数…...
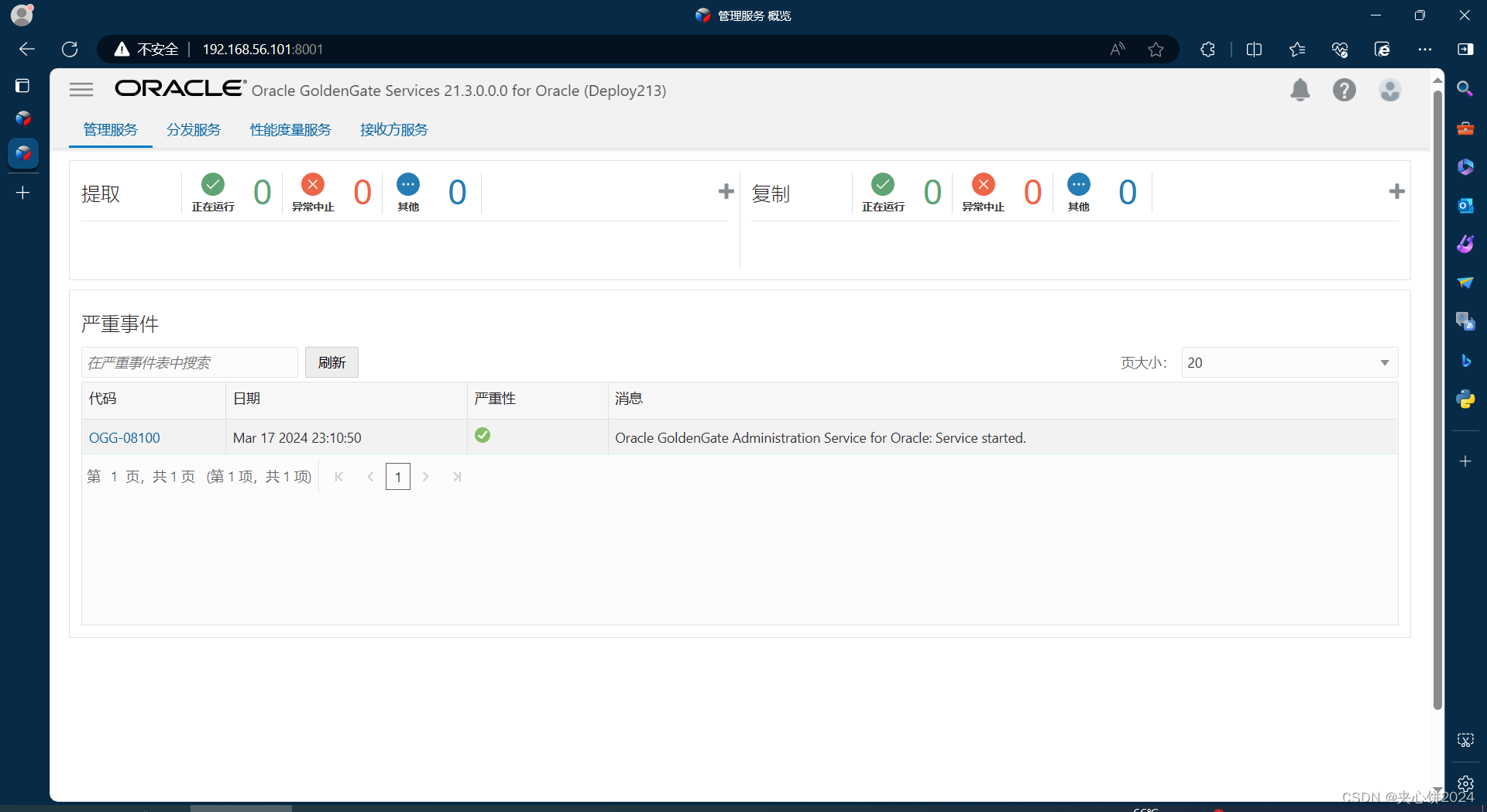
静默安装OGG21.3微服务版本FOR ORACLE版本
静默安装OGG21.3微服务版本FOR ORACLE版本 silent install ogg21.3 for oracle 某度找来找去都没有找到一份可靠的静默安装OGG21.3微服务版本的案例,特别难受,为此将自己静默安装的步骤一步步贴出来分享给大家,请指点,谢谢。 至…...

[二分查找]LeetCode2040:两个有序数组的第 K 小乘积
本文涉及的基础知识点 二分查找算法合集 题目 给你两个 从小到大排好序 且下标从 0 开始的整数数组 nums1 和 nums2 以及一个整数 k ,请你返回第 k (从 1 开始编号)小的 nums1[i] * nums2[j] 的乘积,其中 0 < i < nums1.…...

【Godot4.2】颜色完全使用手册
概述 本篇简单汇总Godot中的颜色的构造和使用,内容包括了: RGB、RGBA,HSV以及HTML16进制颜色值、颜色常量等形式构造颜色颜色的运算以及取反、插值用类型化数组、紧缩数组或PNG图片形式存储多个颜色 构造颜色 因为颜色是一种视觉元素&…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
