Leetcode992-K个不同整数的子数组[两种方法] 关键词 滑窗
文章目录
- 题目
- 方法一:滑窗右端每次+1,左端来回滑动
- 方法二:(最多K种的子串数) - (最多K-1种的子串数) = 恰好K种
题目

1 <= nums.length <= 20000
1 <= nums[i], k <= nums.length
方法一:滑窗右端每次+1,左端来回滑动
这道题初步看上去像滑窗。滑窗解决的问题是“最长”,比如找“无重复字符的最长子串”、“特定排列的子串”。通用方法就是滑窗右侧尽可能向右,直到滑窗内元素的个数不满足要求那么滑窗左侧右移。
本题考虑的不是“最多K个不同整数”,而是“恰好K个不同整数”。
我的办法(方法一)是先用滑窗找到“最多K个不同整数”的每个左右边界,然后对于这其中的每一个右边界,左边界“尝试右移”,找到全部合适的左边界。比如序列12123,对于第二个2来说,“最多2个不同整数”,就是1212,满足条件的左边界有3个,[1]212、[2]12、[1]2.
具体到代码实现,对于每一个右边界(即将加入滑窗)的值来说:
- 如果这个值曾经在滑窗中出现过,则把该值加入滑窗之后,滑窗内仍然是恰好K种数,那么pl“尝试右移”:cnt数组相应减少,直到遇到第一个将cnt的某个非零值减到0位置的位置tmp_pl,那么tmp-pl就是此时右边界对应所有左边界的个数。然后把pl~tmp_pl区间内的数再加回cnt数组(恢复)。
- 如果这个值没有在滑窗中出现,那么把该值加入滑窗之后,滑窗内就有K+1种数了,此时pl必须右移。右移到合适位置后,再进行1中的“尝试右移”操作。
class Solution {int cnt[20010] = {0};int ans = 0;public:int subarraysWithKDistinct(vector<int>& nums, int k) {int pl = 0, pr = 0, k2 = 0;// 先找k个不同的,定下初始滑窗位置 左闭右开for (; pr < nums.size() && k2 < k; pr++)if (++cnt[nums[pr]] == 1) k2++;if (k2 < k) return 0;ans++;// 开始滑动while (pr < nums.size()) {// 先尝试pl右移int tmp_pl = pl;while (cnt[nums[tmp_pl]] > 1) {ans++;cnt[nums[tmp_pl]]--; tmp_pl++;}// 恢复while (tmp_pl > pl) {tmp_pl--;cnt[nums[tmp_pl]]++;}// if 下一个数是旧数,加入if (cnt[nums[pr]] > 0) {cnt[nums[pr]]++; pr++;ans++;}// if 下一个数是新数,pl右移至窗内种类数-1else {cnt[nums[pr]]++; pr++;do {cnt[nums[pl]]--;pl++;} while (cnt[nums[pl - 1]] > 0);ans++;}}// 尝试pl右移int tmp_pl = pl;while (cnt[nums[tmp_pl]] > 1) {ans++;cnt[nums[tmp_pl]]--;tmp_pl++;}return ans;}
};
时间复杂度:最坏是Onn,但是实际还不错。

方法二:(最多K种的子串数) - (最多K-1种的子串数) = 恰好K种
这个方法是官方题解法。
还是12123,且K=2这个例子,对于1212来说,有3个左边界可以满足“恰好K种”,这个3是怎么算出来的呢?最多K-1种的左边界是1个,一共4个潜在的左边界,4-1=3.
(最多K种的子串数) - (最多K-1种的子串数) = 恰好K种
时间复杂度On
相关文章:

Leetcode992-K个不同整数的子数组[两种方法] 关键词 滑窗
文章目录 题目方法一:滑窗右端每次1,左端来回滑动方法二:(最多K种的子串数) - (最多K-1种的子串数) 恰好K种 题目 1 < nums.length < 20000 1 < nums[i], k < nums.length 方法一…...
【闲聊】-后端框架发展史
框架,是为了解决系统复杂性,提升开发效率而产生的工具,主要服务于研发人员。 当然,框架还有更深层的作用,框架的沉淀是一种高级的抽象,会将人类的业务逐步抽象为统一标准又灵活可变的结构,为各行…...
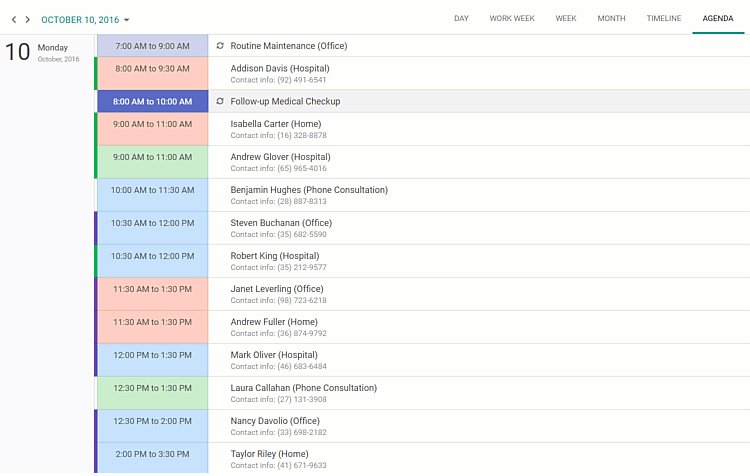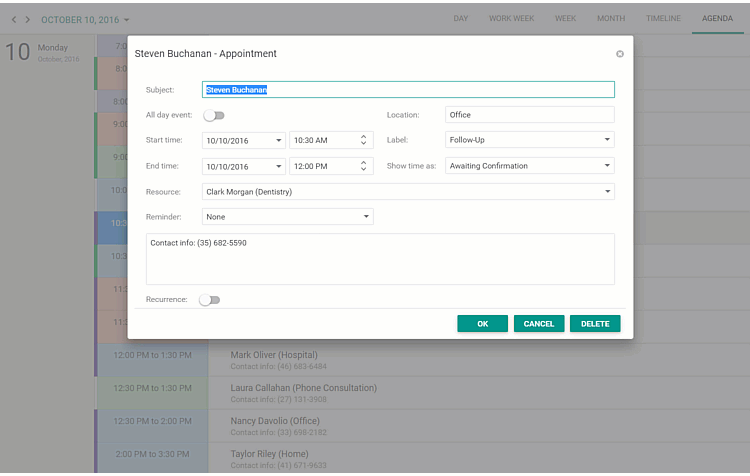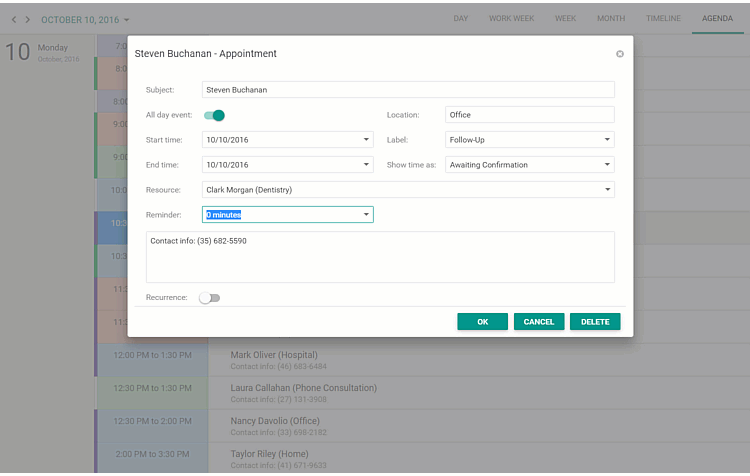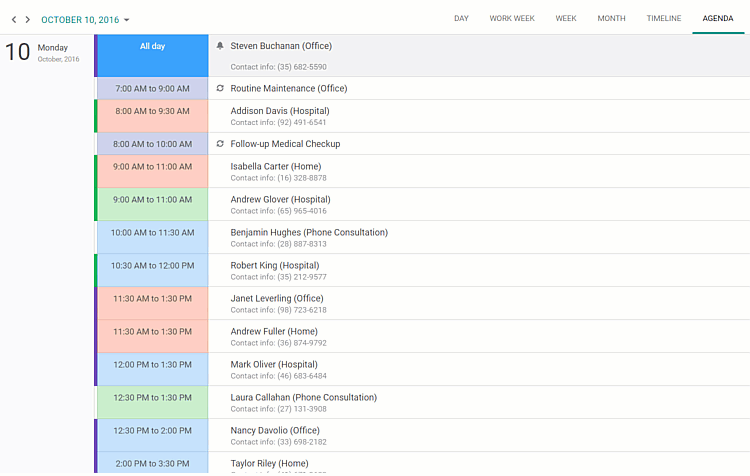
界面控件DevExpress ASP.NET Scheduler - 助力快速交付个人信息管理系统(下)
DevExpress ASP. NET Scheduler组件能完全复制Microsoft Outlook Scheduler的样式和功能,具有日、周、月和时间轴视图,并包括内置的打印支持,因此用户可以在尽可能短的时间内交付全功能的个人信息管理系统。在上文中(点击这里回顾…...
机器学习-04-分类算法-01决策树
总结 本系列是机器学习课程的系列课程,主要介绍机器学习中分类算法,本篇为分类算法开篇与决策树部分。 参考 决策树——ID3和C4.5(理论图解公式推导) 策略产品经理必读系列—第七讲ID3、C4.5和CART算法详解 决策树(…...

探索大数据时代的决策利器:如何有效应对海量数据?
随着信息技术的快速发展,大数据时代已经到来,海量数据成为了我们生活和工作中不可忽视的一部分。这些数据来自各个方面:社交媒体、传感器、网络交易、移动设备等,每天都在以惊人的速度增长。但是,面对如此庞大的数据量,我们该如何有效地应对呢?本文将探索大数据时代的决…...
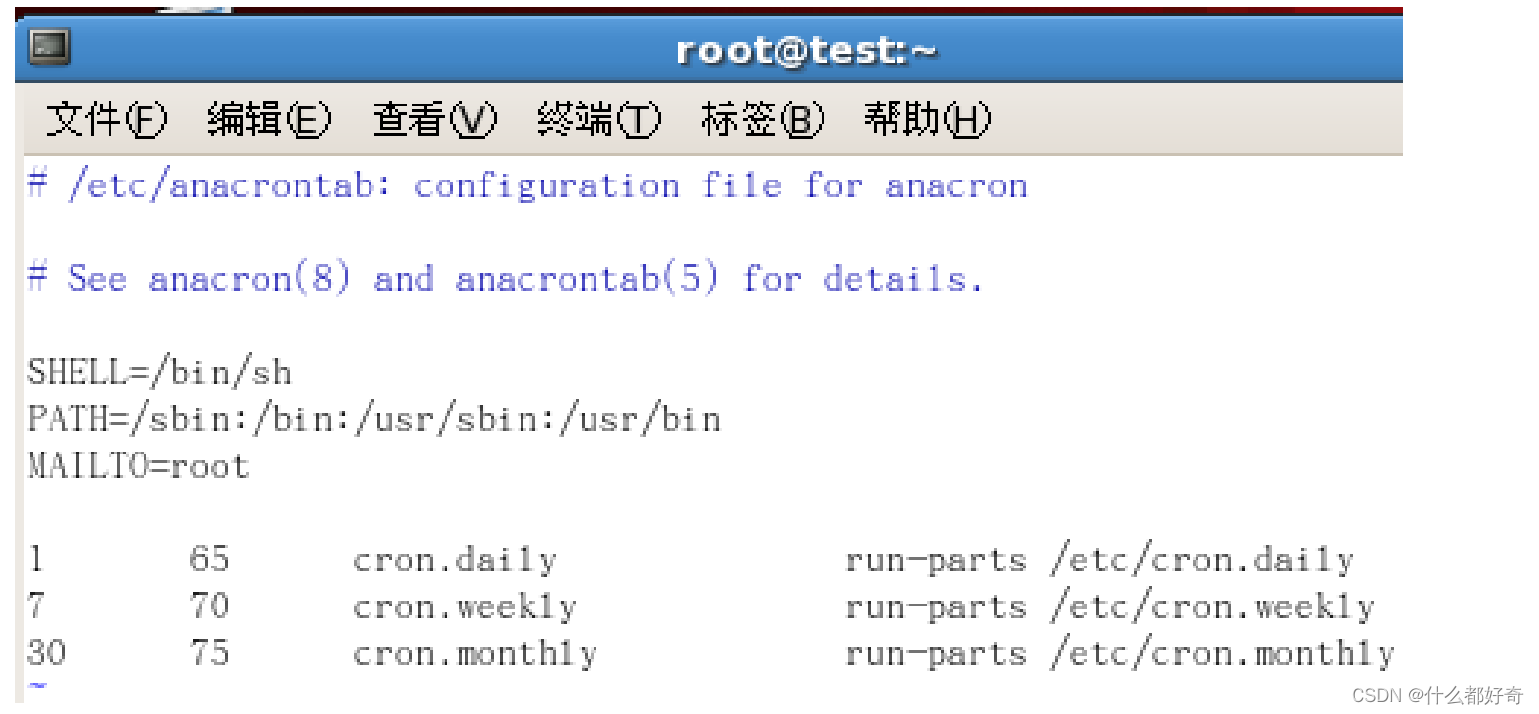
Linux 学习笔记(16)
十六、 计划任务 在很多时候为了自动化管理系统,我们都会用到计划任务,比如关机,管理,备份之类的操作,我 们都可以使用计划任务来完成,这样可以是管理员的工作量大大降低,而且可靠度更好。 l…...

【C语言】打印闰年
输⼊⼀个年份year,判断year是否是闰年 闰年判断的规则: 1, 能被4整除并且不能被100整除是闰年 2,能被400整除是闰年 结合起来如下: if ((year % 4 0 && year % 100 ! 0) || (year % 400 0)) 代码如下&…...

外贸入门,很残忍但很真实的外贸真相
如果你是小白入行外贸,第一家选择的公司大概率会决定你以后的客户开发模式。 外贸老鸟们可以留言讨论下自己是不是被说中了。 如果新人选择的第一家公司是靠B2B网站,展会或者官网询盘分发,公司每年会花大量的广告费用获客,你会很快…...
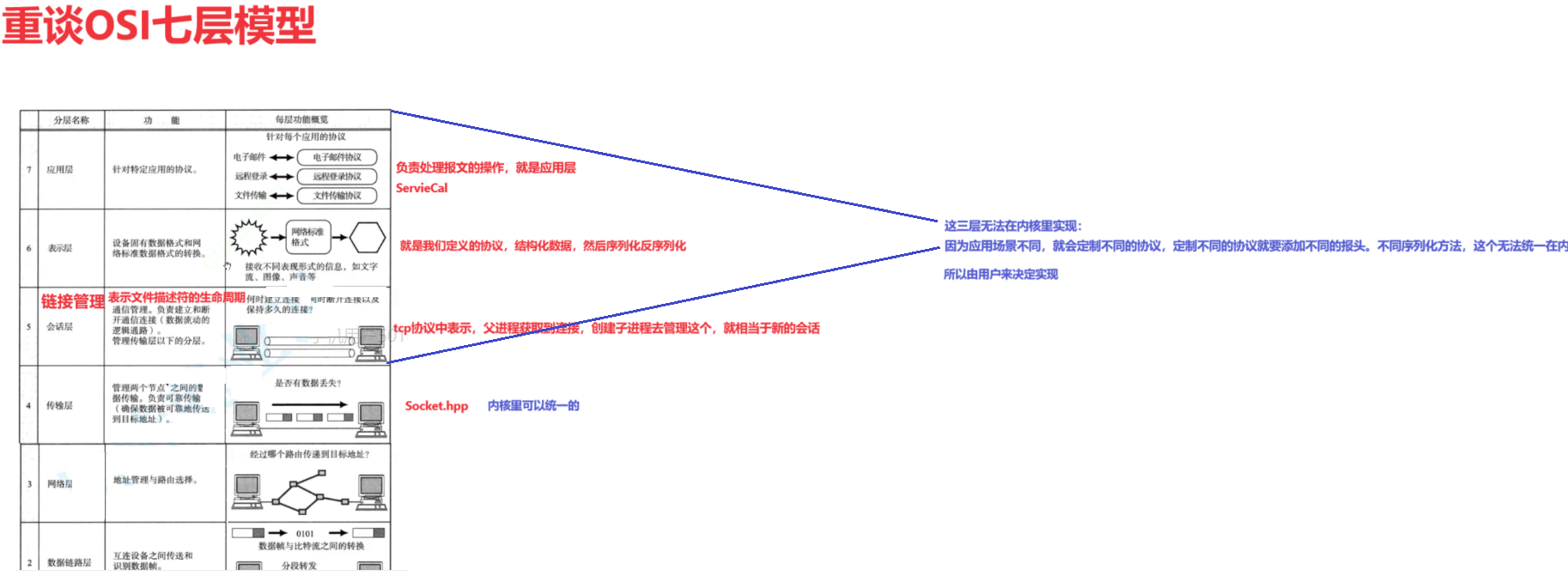
【Linux网络编程七】网络序列化和反序列化(网络版本计算器)
【Linux网络编程七】网络序列化和反序列化(网络版本计算器) 一.网络读取问题【解决方案】1.定制协议2.序列化和反序列化3.添加报头①封包②解包 4.框架总结 二.自定义协议:网络计算器协议Ⅰ.客户端发送请求,服务器端接收请求1.构建请求(结构化…...
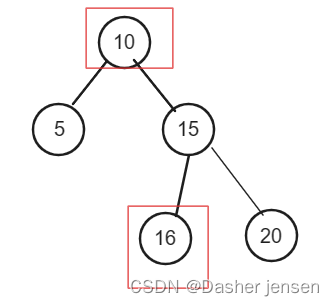
算法打卡day17|二叉树篇06|Leetcode 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
算法题 Leetcode 654.最大二叉树 题目链接:654.最大二叉树 大佬视频讲解:最大二叉树视频讲解 个人思路 大概思路就是在数组中 找最大值的节点作为当前节点,用最大值的index切割左右子树的区间,往复循环到数组元素为0; 解法 递…...
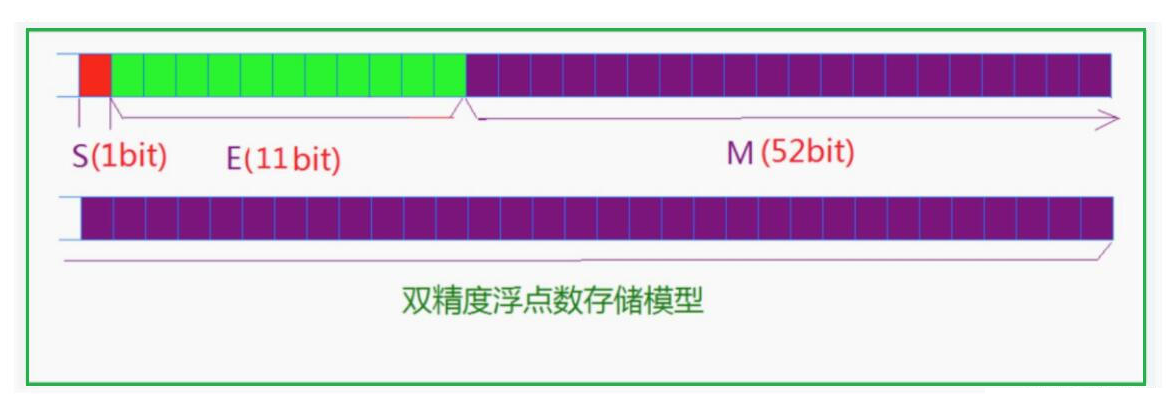
C语言之数据在计算机内部的存储
文章目录 一、前言二、类型的基本归类1、整型家族2、浮点数家族3、构造类型4、指针类型 三、整型在内存中的存储1、原码、反码、补码1.1 概念1.2 原码与补码的转换形式1.3 计算机内部的存储编码 2、大小端介绍~~2.1 为什么要有大端和小端之分?2.2 大(小&…...
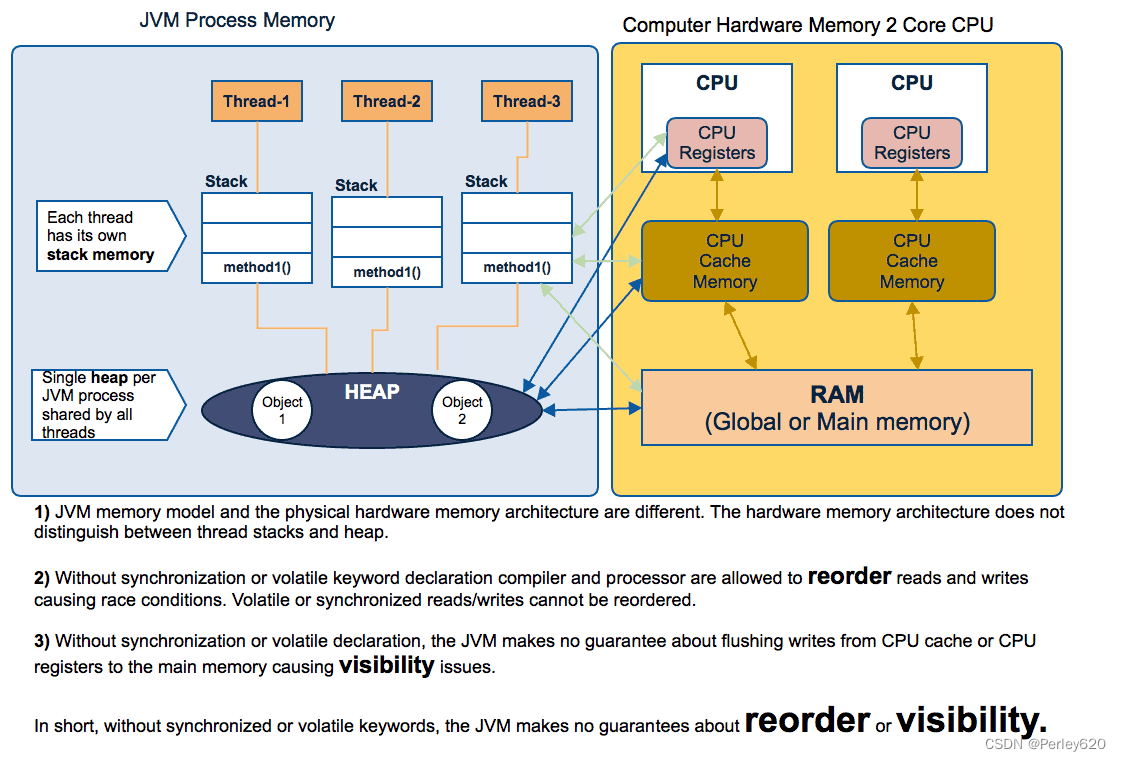
程序人生——Java中基本类型使用建议
目录 引出Java中基本类型使用建议建议21:用偶判断,不用奇判断建议22:用整数类型处理货币建议23:不要让类型默默转换建议24:边界、边界、还是边界建议25:不要让四舍五入亏了一方 建议26:提防包装…...

Pikachu 靶场搭建
文章目录 环境说明1 Pikachu 简介2 Pikachu 安装 环境说明 操作系统:Windows 10PHPStudy 版本: 8.1.1.3Apache 版本:2.4.39MySQL 版本 5.7.26 1 Pikachu 简介 Pikachu是一个使用“PHP MySQL” 开发、包含常见的Web安全漏洞、适合Web渗透测试学习人员练…...

机器学习-绪论
机器学习致力于研究如何通过计算的手段、利用经验来改善系统自身的性能。在计算机系统中,“经验”通常以“数据”的形式存在,因此,机器学习所研究的主要内容,是关于在计算机上从数据中产生“模型”的算法,即“学习算法…...
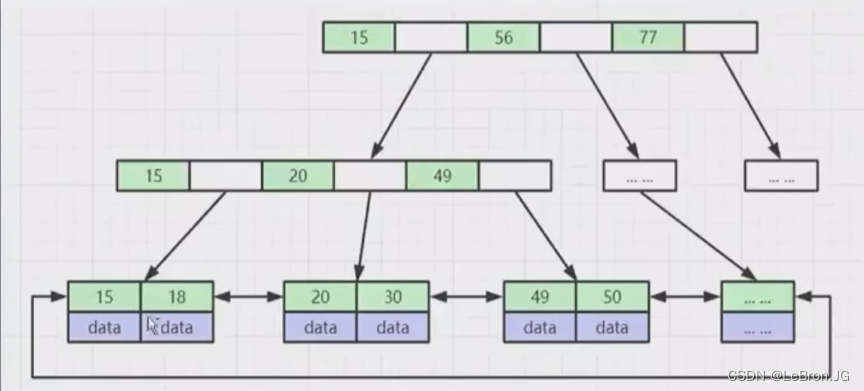
mysql 索引(为什么选择B+ Tree?)
索引实现原理 索引:排好序的数据结构 优点:降低I/O成本,CPU的资源消耗(数据持久化在磁盘中,每次查询都得与磁盘交互) 缺点:更新表效率变慢,(更新表数据,还要…...

蓝桥杯-带分数
法一 /* 再每一个a里去找c,他们共用一个st数组,可以解决重复出现数字 通过ac确定b,b不能出现<0 b出现的数不能和ac重复*/import java.util.Scanner;public class Main {static int n,res;static boolean[] st new boolean[15];static boolean[] backup new boolean[15];…...
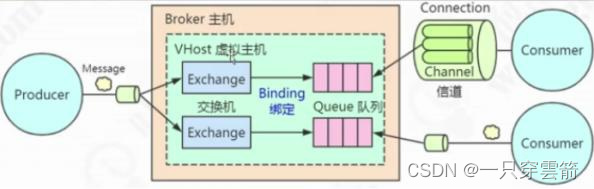
消息队列面试题
目录 1. 为什么使用消息队列 2. 消息队列的缺点 3. 消息队列如何选型? 4. 如何保证消息队列是高可用的 5. 如何保证消息不被重复消费(见第二条) 6. 如何保证消息的可靠性传输? 7. 如何保证消息的顺序性(即消息幂…...

Android和IOS应用开发-Flutter 应用中实现记录和使用全局状态的几种方法
文章目录 在Flutter中记录和使用全局状态使用 Provider步骤1步骤2步骤3 使用 BLoC步骤1步骤2步骤3 使用 GetX:步骤1步骤2步骤3 在Flutter中记录和使用全局状态 在 Flutter 应用中,您可以使用以下几种方法来实现记录和使用全局状态,并在整个应…...

若依 ruoyi-cloud [网关异常处理]请求路径:/system/user/getInfo,异常信息:404
这里遇到的情况是因为nacos中的配置文件与项目启动时的编码不一样,若配置文件中有中文注释,那么用idea启动项目的时候,在参数中加上 -Dfile.encodingutf-8 ,保持编码一致,(用中文注释的配置文件,…...
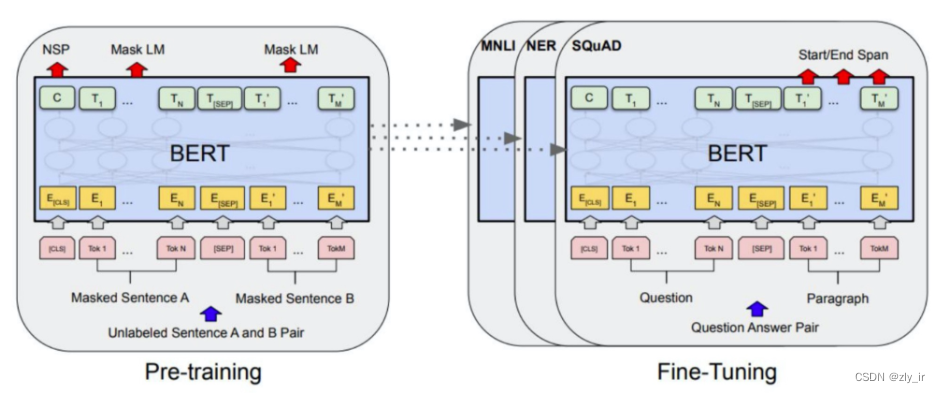
自然语言处理里预训练模型——BERT
BERT,全称Bidirectional Encoder Representation from Transformers,是google在2018年提出的一个预训练语言模型,它的推出,一举刷新了当年多项NLP任务值的新高。前期我在零、自然语言处理开篇-CSDN博客 的符号向量化一文中简单介绍…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
