矩阵A的LU分解
文章目录
- 1. 矩阵的逆矩阵
- 1.1 AB的逆矩阵
- 1.2 转置矩阵
- 2. 2X2矩阵A消元
- 3. 3X3矩阵A消元
- 4. 运算量
- 5. 置换矩阵-左行右列
本文主要目的是为了通过矩阵乘法实现矩阵A的分解。
1. 矩阵的逆矩阵
1.1 AB的逆矩阵
- 假设A,B矩阵都可逆
A ( B B − 1 ) A − 1 = I (1) A(BB^{-1})A^{-1}=I\tag{1} A(BB−1)A−1=I(1) - 可得如下
( A B ) ( B − 1 A − 1 ) = I (2) (AB)(B^{-1}A^{-1})=I\tag{2} (AB)(B−1A−1)=I(2) - 所以当AB矩阵单独可逆下:
( A B ) − 1 = B − 1 A − 1 (3) (AB)^{-1}=B^{-1}A^{-1}\tag{3} (AB)−1=B−1A−1(3)
1.2 转置矩阵
- 由于矩阵A满足如下条件
A A − 1 = I (4) AA^{-1}=I\tag{4} AA−1=I(4) - 对等式两边进行转置如下:
( A − 1 ) T A T = I T = I (5) (A^{-1})^TA^T=I^T=I\tag{5} (A−1)TAT=IT=I(5) - 由此可得如下:
( A T ) − 1 = ( A − 1 ) T (6) (A^T)^{-1}=(A^{-1})^{T}\tag{6} (AT)−1=(A−1)T(6)
2. 2X2矩阵A消元
假设矩阵A经过行与行之间的计算,可以得到上三角矩阵U ,可以简化成如下,
E 21 = [ 1 0 − 4 1 ] ; A = [ 2 1 8 7 ] ; U = [ 2 1 0 3 ] ; (7) E_{21}=\begin{bmatrix}1&0\\\\-4&1\end{bmatrix};A=\begin{bmatrix}2&1\\\\8&7\end{bmatrix};U=\begin{bmatrix}2&1\\\\0&3\end{bmatrix};\tag{7} E21= 1−401 ;A= 2817 ;U= 2013 ;(7)
E 21 A = U (8) E_{21}A=U\tag{8} E21A=U(8)
[ 1 0 − 4 1 ] [ 2 1 8 7 ] = [ 2 1 0 3 ] (9) \begin{bmatrix}1&0\\\\-4&1\end{bmatrix}\begin{bmatrix}2&1\\\\8&7\end{bmatrix}=\begin{bmatrix}2&1\\\\0&3\end{bmatrix}\tag{9} 1−401 2817 = 2013 (9)
- 可以将上式改成如下
A = ( E 21 ) − 1 U = L U (10) A=(E_{21})^{-1}U=LU\tag{10} A=(E21)−1U=LU(10) - ( E 21 ) − 1 (E_{21})^{-1} (E21)−1可得如下:
( E 21 ) − 1 = [ 1 0 4 1 ] (11) (E_{21})^{-1}=\begin{bmatrix}1&0\\\\4&1\end{bmatrix}\tag{11} (E21)−1= 1401 (11) - 将U进行分解可得
U = [ 2 1 0 3 ] = [ 2 0 0 3 ] [ 1 1 2 0 1 ] (12) U=\begin{bmatrix}2&1\\\\0&3\end{bmatrix}=\begin{bmatrix}2&0\\\\0&3\end{bmatrix}\begin{bmatrix}1&\frac{1}{2}\\\\0&1\end{bmatrix}\tag{12} U= 2013 = 2003 10211 (12) - 综上所述可得如下:
A = [ 2 1 8 7 ] ; L = [ 1 0 4 1 ] ; D = [ 2 0 0 3 ] ; U = [ 1 1 2 0 1 ] (13) A=\begin{bmatrix}2&1\\\\8&7\end{bmatrix};L=\begin{bmatrix}1&0\\\\4&1\end{bmatrix};D=\begin{bmatrix}2&0\\\\0&3\end{bmatrix};U=\begin{bmatrix}1&\frac{1}{2}\\\\0&1\end{bmatrix}\tag{13} A= 2817 ;L= 1401 ;D= 2003 ;U= 10211 (13) - A = L D U A=LDU A=LDU
[ 2 1 8 7 ] = [ 1 0 4 1 ] [ 2 0 0 3 ] [ 1 1 2 0 1 ] (14) \begin{bmatrix}2&1\\\\8&7\end{bmatrix}=\begin{bmatrix}1&0\\\\4&1\end{bmatrix}\begin{bmatrix}2&0\\\\0&3\end{bmatrix}\begin{bmatrix}1&\frac{1}{2}\\\\0&1\end{bmatrix}\tag{14} 2817 = 1401 2003 10211 (14)
3. 3X3矩阵A消元
- 同理假设有一个3X3矩阵,我们可以经过行变换来消元。
E 32 E 31 E 21 A = U (15) E_{32}E_{31}E_{21}A=U\tag{15} E32E31E21A=U(15) - 求逆矩阵如下:
L = ( E 21 ) − 1 ( E 31 ) − 1 ( E 32 ) − 1 (16) L=(E_{21})^{-1}(E_{31})^{-1}(E_{32})^{-1}\tag{16} L=(E21)−1(E31)−1(E32)−1(16)
A = ( E 21 ) − 1 ( E 31 ) − 1 ( E 32 ) − 1 U (17) A=(E_{21})^{-1}(E_{31})^{-1}(E_{32})^{-1}U\tag{17} A=(E21)−1(E31)−1(E32)−1U(17) - 假设如下矩阵:
E 21 = [ 1 0 0 − 2 1 0 0 0 1 ] ; E 31 = [ 1 0 0 0 1 0 0 0 1 ] ; E 32 = [ 1 0 0 0 1 0 0 − 5 1 ] ; (18) E_{21}=\begin{bmatrix}1&0&0\\\\-2&1&0\\\\0&0&1\end{bmatrix};E_{31}=\begin{bmatrix}1&0&0\\\\0&1&0\\\\0&0&1\end{bmatrix};E_{32}=\begin{bmatrix}1&0&0\\\\0&1&0\\\\0&-5&1\end{bmatrix};\tag{18} E21= 1−20010001 ;E31= 100010001 ;E32= 10001−5001 ;(18)
E 3221 = E 32 E 21 = [ 1 0 0 − 2 1 0 10 − 5 1 ] (19) E_{3221}=E_{32}E_{21}=\begin{bmatrix}1&0&0\\\\-2&1&0\\\\10&-5&1\end{bmatrix}\tag{19} E3221=E32E21= 1−21001−5001 (19)
E 21 = [ 1 0 0 − 2 1 0 0 0 1 ] ; ⇒ ( E 21 ) − 1 = [ 1 0 0 2 1 0 0 0 1 ] ; (20) E_{21}=\begin{bmatrix}1&0&0\\\\-2&1&0\\\\0&0&1\end{bmatrix};\Rightarrow(E_{21})^{-1}=\begin{bmatrix}1&0&0\\\\2&1&0\\\\0&0&1\end{bmatrix};\tag{20} E21= 1−20010001 ;⇒(E21)−1= 120010001 ;(20)
E 32 = [ 1 0 0 0 1 0 0 − 5 1 ] ; ⇒ ( E 32 ) − 1 = [ 1 0 0 0 1 0 0 5 1 ] ; (20) E_{32}=\begin{bmatrix}1&0&0\\\\0&1&0\\\\0&-5&1\end{bmatrix};\Rightarrow(E_{32})^{-1}=\begin{bmatrix}1&0&0\\\\0&1&0\\\\0&5&1\end{bmatrix};\tag{20} E32= 10001−5001 ;⇒(E32)−1= 100015001 ;(20)
L = ( E 3221 ) − 1 = ( E 21 ) − 1 ( E 32 ) − 1 = [ 1 0 0 2 1 0 0 5 1 ] ; (21) L=(E_{3221})^{-1}=(E_{21})^{-1}(E_{32})^{-1}=\begin{bmatrix}1&0&0\\\\2&1&0\\\\0&5&1\end{bmatrix};\tag{21} L=(E3221)−1=(E21)−1(E32)−1= 120015001 ;(21) - 综上所述:
A = L U (22) A=LU\tag{22} A=LU(22)
4. 运算量
- 假设我们矩阵A是100X100的矩阵,那么将矩阵A通过行变换分解成A=LU 一共要进行如下计算步骤:
C o u n t = n 2 + ( n − 1 ) 2 + ⋯ + 2 2 + 1 2 = 1 3 n 3 = 1000000 3 (23) Count=n^2+(n-1)^2+\dots+2^2+1^2=\frac{1}{3}n^3=\frac{1000000}{3}\tag{23} Count=n2+(n−1)2+⋯+22+12=31n3=31000000(23)
5. 置换矩阵-左行右列
- 左乘置换矩阵-进行行变换XA
- 右乘置换矩阵-进行列变换AX
- 置换矩阵指的是一列中只有一个位置为1,同一列其他位置均为0,用来对矩阵进行位置交换。
- 第一行和第二行位置交换
A = [ 1 2 3 4 5 6 7 8 9 ] (24) A=\begin{bmatrix}1&2&3\\\\4&5&6\\\\7&8&9\end{bmatrix}\tag{24} A= 147258369 (24)
B = [ 4 5 6 1 2 3 7 8 9 ] = [ 0 1 0 1 0 0 0 0 1 ] [ 1 2 3 4 5 6 7 8 9 ] (25) B=\begin{bmatrix}4&5&6\\\\1&2&3\\\\7&8&9\end{bmatrix}=\begin{bmatrix}0&1&0\\\\1&0&0\\\\0&0&1\end{bmatrix}\begin{bmatrix}1&2&3\\\\4&5&6\\\\7&8&9\end{bmatrix}\tag{25} B= 417528639 = 010100001 147258369 (25)
相关文章:

矩阵A的LU分解
文章目录 1. 矩阵的逆矩阵1.1 AB的逆矩阵1.2 转置矩阵 2. 2X2矩阵A消元3. 3X3矩阵A消元4. 运算量5. 置换矩阵-左行右列 本文主要目的是为了通过矩阵乘法实现矩阵A的分解。 1. 矩阵的逆矩阵 1.1 AB的逆矩阵 假设A,B矩阵都可逆 A ( B B − 1 ) A − 1 I (1) A(BB^{-1})A^{-1}…...

深入了解Flutter中Future的全部工厂方法及使用
在Flutter中,Future是一种表示异步操作结果的对象。它代表了一个可能已经完成或尚未完成的计算,可以用来处理异步任务。Flutter提供了多种工厂方法来创建Future对象,每种方法都有其特定的用途和优势。在本文中,我们将深入探讨Flut…...

python的BBS论坛系统flask-django-nodejs-php
为了更好地发挥本系统的技术优势,根据BBS论坛系统的需求,本文尝试以B/S架构设计模式中的django/flask框架,python语言为基础,通过必要的编码处理、BBS论坛系统整体框架、功能服务多样化和有效性的高级经验和技术实现方法ÿ…...
vulnhub-----pWnOS1.0靶机
文章目录 1.信息收集2.漏洞测试3.爆破hash4.提权 首先拿到一台靶机,就需要知道靶机的各种信息(IP地址,开放端口,有哪些目录,什么框架,cms是什么,网页有什么常见的漏洞,如sql注入&…...

vue 消息左右滚动(前后无缝衔接)
演示效果 封装的组件 <!--* Author:* Date: 2024-03-21 19:21:58* LastEditTime: 2024-03-21 20:31:50* LastEditors: Please set LastEditors* Description: 消息左右滚动 --> <template><divid"textScroll"class"text-scroll"mousemove&…...
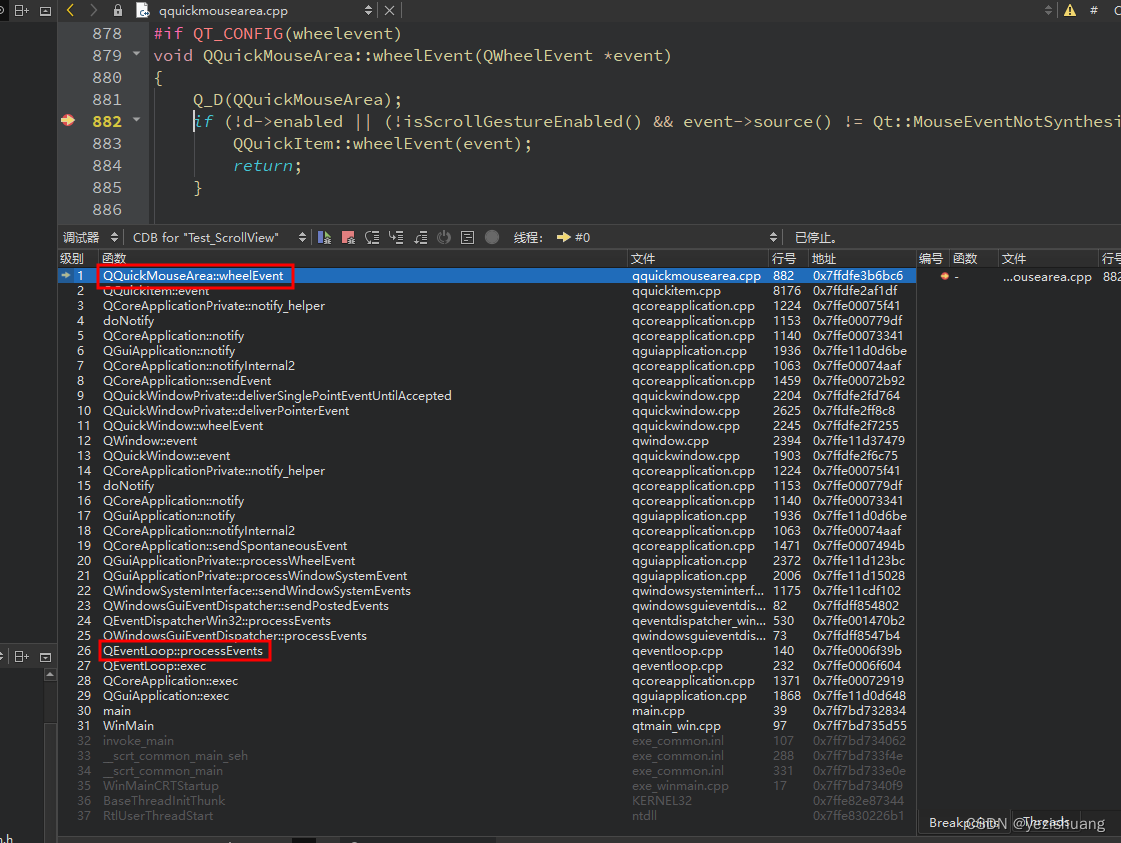
Qt如何直接处理系统事件(比如鼠标事件),而不是post事件
#include <QtGui/5.15.2/QtGui/qpa/qwindowsysteminterface.h> // 方便调试事件 QWindowSystemInterface::setSynchronousWindowSystemEvents(true); 直接再 qWindowsWndProc函数中处理 通常情况: 事件被放到一个队列中...

Web前端笔记+表单练习+五彩导航
一、笔记 表单:数据交互的一种方式 登录、注册、搜索 <from> <input type""> --- <input type"text"> --- 普通输入框,内容在一行显示 <input type"password"> --- 密码框 <input type"…...
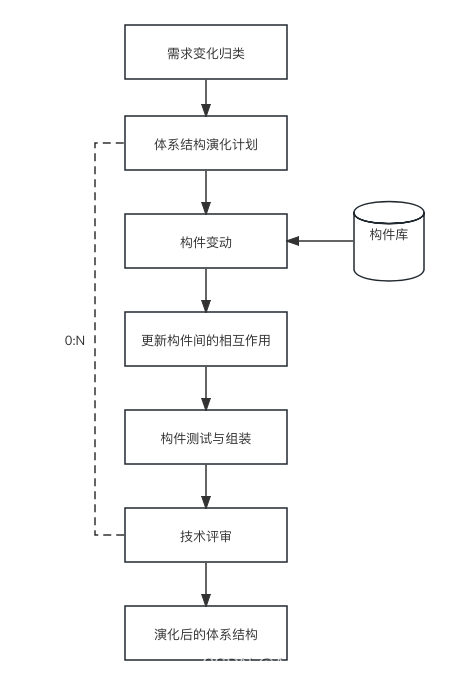
软件架构和基于架构的软件开发方法知识总结
一、软件架构定义 软件架构为软件系统提供了一个结构、行为和属性的高级抽象 软件架构是一种表达,使软件工程师能够: (1)分析设计在满足所规定的需求方面的有效性 (2)在设计变更相对容易的阶段,…...
环信新版单群聊UIKit集成指南——Android篇
前言 环信新版UIKit已重磅发布!目前包含单群聊UIKit、聊天室ChatroomUIKit,本文详细讲解Android端单群聊UIKit的集成教程。 环信单群聊 UIKit 是基于环信即时通讯云 IM SDK 开发的一款即时通讯 UI 组件库,提供各种组件实现会话列表、聊天界…...

最细致最简单的 Arm 架构搭建 Harbor
更好的阅读体验:点这里 ( www.doubibiji.com ) ARM离线版本安装 官方提供了一个 arm 版本,但是好久都没更新了,地址:https://github.com/goharbor/harbor-arm 。 也不知道为什么不更新,我看…...

mysql基础02
1.常用函数 字符串处理函数 length(str) 统计字符长度char_length(str) 统计以(单个字符为单位)的字符长度ucase/upper(str) 小写变大写lcase/lower(str) 大写变小写substr(s,start,end) 从s截start到end的字符串instr(str,"str1") str1在str的位置是? trim(str) 去…...

css的box-shadow详解
CSS的box-shadow属性用于在元素框上添加阴影效果。它可以为元素提供外阴影或内阴影,并且可以控制阴影的颜色、偏移距离、模糊半径以及扩展半径。 box-shadow属性的基本语法如下: box-shadow: h-shadow v-shadow blur spread color inset;下面是各个参数…...

递归的个人总结
递归函数(递去、回归)是函数不断的调用自己; 可以按照如下来理解:func1中调用func2,func2中调用func3; func3函数返回了,继续执行func2中的语句;func2执行完了,继续执行func1之后的…...
使用PDFBox调整PDF每页格式
目录 一、内容没有图片 二、内容有图片 maven依赖,这里使用的是pdfbox的2.0.30版本 <dependency><groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>2.0.30</version></dependency>…...
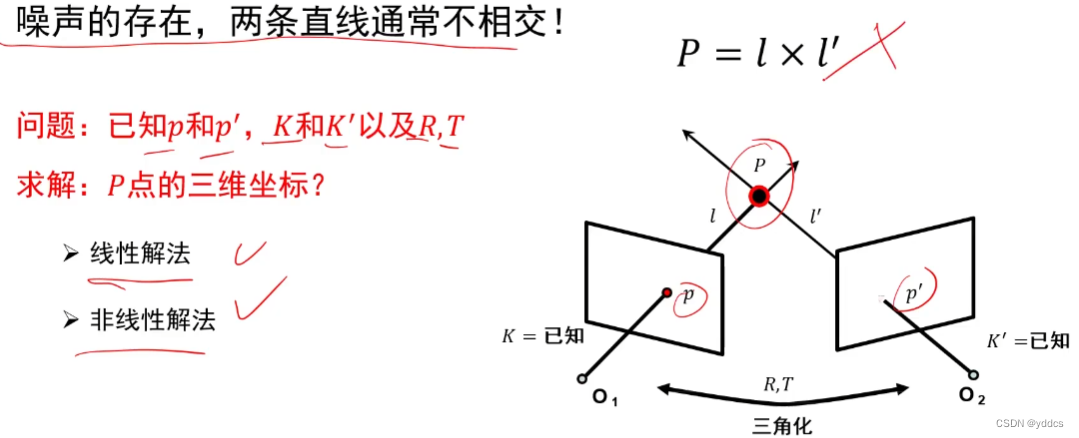
【3D reconstruction 学习笔记】
三维重建 3D reconstruction 1. 相机几何针孔相机摄像机几何 2. 相机标定线性方程组的解齐次线性方程组的解非线性方程组的最小二乘解透镜相机标定带畸变的相机标定 3. 单视图重建2D平面上的变换3D空间上的变换单视测量无穷远点 无穷远线 无穷远平面影消点 影消线单视重构 4. 三…...
(附源码)基于Spring Boot与Vue的宠物用品销售系统设计与实现
前言 💗博主介绍:✌专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻 精彩专栏 推荐订阅👇🏻 2024年Java精品实战案例《100套》 🍅文末获取源码联系🍅 ἱ…...

Qwen及Qwen-audio大模型微调项目汇总
Qwen及Qwen-audio可微调项目调研 可用来微调方法/项目汇总ps.大语言模型基础资料 可用来微调方法/项目汇总 Qwen github 项目自带的finetune脚本 可以参考https://blog.csdn.net/qq_45156060/article/details/135153920PAI-DSW中微调千问大模型(阿里云的一个产品&a…...
浅析ArcGis中的软件——ArcMap、ArcScene、 ArcGlobe、ArcCatalog
为什么要写这么一篇介绍ArcGis的文章呢?因为大部分人也包括ArcGisdada,在使用ArcMap应用程序创建工程时总以为我们就是使用了ArcGis这个软件的所有。其实不然,在后期的接触和使用中慢慢发现原来ArcMap只是ArcGis这个综合平台的一部分…...

AndroidStudio插件出现“Compatible with IntelliJ IDEA only“错误时的解决方案
原因:插件比较老,配置可能存在问题 1.修改plugins文件夹下的jar包(插件) 找到AndroidStudio所在位置 打开plugins文件夹,找到需要修改的jar包,通过压缩软件用zip方式打开,找到\META-INF\plugin.xml并编辑,在<version>xxxx</versi…...

探索未来的编程趋势与挑战
摘要: 本文将探讨未来编程领域可能面临的挑战和发展趋势,包括人工智能、量子计算、区块链等新兴技术对编程的影响,以及程序员需要具备的新技能和素质。 随着人工智能技术的快速发展,机器学习、深度学习等算法在编程领域的应用越来…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
