力扣● 503.下一个更大元素II ● 42. 接雨水
- 503.下一个更大元素II
与496.下一个更大元素 I的不同是要循环地搜索元素的下一个更大的数。那么主要是对于遍历结束后,单调栈里面剩下的那些元素。
如果直接把两个数组拼接在一起,然后使用单调栈求下一个最大值就可以。
代码实现的话,不用直接把数组后面再接一个数组,而是单调栈走2遍这个数组即可。
代码如下。第二次遍历使用取余的方法。
class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n=nums.size();vector<int> result(n,-1);stack<int> st;for(int i=0;i<2*n;++i){int k=i%n;while(!st.empty() && nums[k]>nums[st.top()]){result[st.top()]=nums[k];st.pop();}st.push(k);}return result;}
};- 42. 接雨水
依据列来计算更好理解,能引入单调栈:可以看出,因为左侧最高柱子和右侧最高柱子肯定不会存储雨水(左侧和右侧包含自己,因为自己是一侧最高的话不会存储雨水),所以每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
下面图片以柱子4为例,可以看见中间所有柱子都满足这个结论,最两边的柱子不会存储雨水。
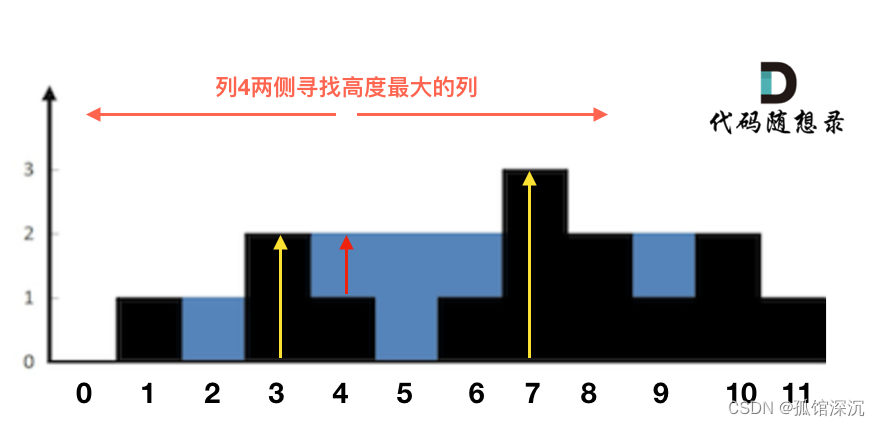
转化问题后,有3种办法解决:
- 会超时的暴力解法。
- 双指针优化。
- 重点的单调栈。
1、暴力解法。
对于每个元素,都从左、从右找最大高度的柱子lheight、rheight,所以外层循环是0到n-1,内层循环从i往左,然后从i往右找最大高度的柱子lheight、rheight,最多会查找n次。所以时间复杂度是O(n^2),空间复杂度O(1)。但是会超时。
2、双指针优化。
当前元素的左边、右边最大高度的柱子lheight、rheight其实跟前一个元素的lheight、rheight有关。注意左边最大和右边最大要把自己考虑进去,如果不包含,左边最大/右边最大的可能比自己还小,那么相减是负数,最终结果比正确结果小。
当前i的lheight取决于左边i-1的lheight,rheight取决于右边i+1的rheight。具体如下:
当前i的lheight=max(前一个lheight,height[i]),所以需要从左到右得到lheight。
那么参照lheight,当前i的rheight应该=max(后一个lheight,height[i]),与上面相反,从右到左得到。
根据这个过程先把所有元素的lheight数组和rheight数组求出来,然后再遍历元素的时候,直接就是min(lheight[i],rheight[i])-height[i]。时间复杂度是O(n),空间复杂度O(n)。
代码如下。
class Solution {
public:int trap(vector<int>& height) {int n=height.size();int l1,r1,l2,r2;int count=0;vector<int> lheight(n);vector<int> rheight(n);//初始化lheight[0]=height[0];rheight[n-1]=height[n-1];for(int i=1;i<n-1;++i){//中间元素的lheight和rheightlheight[i]=max(lheight[i-1],height[i]);rheight[i]=max(rheight[i+1],height[i]);}for(int i=n-2;i>0;--i){rheight[i]=max(rheight[i+1],height[i]);}for(int i=0;i<n;++i){if(i==0 || i==n-1)continue;int cur=min(lheight[i],rheight[i])-height[i];count+=cur;}return count;}
};上面的1、2都是按照列的方式去装水,因为是找左右两边最大元素。
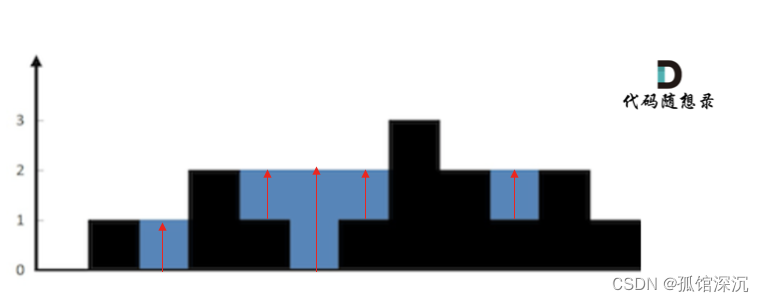
3、单调栈
如果按行装水的话,就可以通过下一个更大元素和上一个最大元素来求。
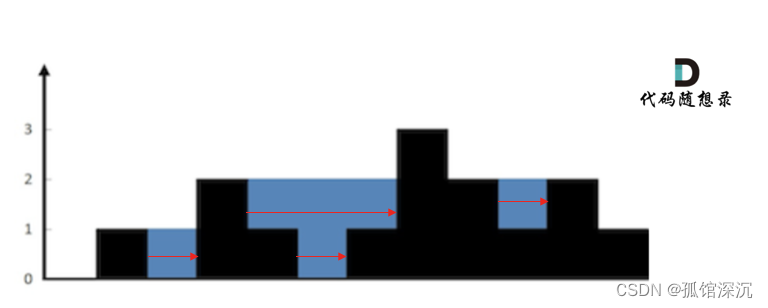
以上图为例,下标2左边更大是1,右边更大是2,所以自己这行(以下标2柱高0为底,以min(左边更大值,右边更大值)为高,宽度是2个更大值的距离1)可以存储1的雨水;下标4左边更大是2,右边更大是3,所以自己这行(以下标4柱高1为底,以min(左边更大值,右边更大值)=2为高,宽度是2个更大值的距离3)可以存储3的雨水……左边更大和右边更大有1个不存在的则存储雨水为0。
所以要用单调栈计算出上一个更大值和下一个更大值的下标leftmax和rightmax。然后i柱子处可以存储的雨水是:(min(height[leftmax],height[rightmax])-height[i])*(rightmax-leftmax-1)。
怎么计算上一个更大值和下一个更大值呢?还想着2次单调栈,实际上,1次单调栈即可。采用单调递增栈,在元素 i 比栈顶大的情况下,如果栈顶同时也比次栈顶要小,这个时候就出现一个凹槽,也就找到了上一个更大值(次栈顶)和下一个更大值(元素i)。所以这个单调递增栈,必须是严格的单增,这个凹槽一定是次栈顶>栈顶<比栈顶大的元素i。
所以如果元素i==栈顶的话,要么不操作,要么替换这个栈顶,才能满足单调栈。这里需要选择的操作是替换栈顶,因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
如果<栈顶,就直接入栈。
清晰说明了3种情况:
class Solution {
public:int trap(vector<int>& height) {int n=height.size();int count=0;stack<int> st;st.push(0);for(int i=1;i<n;++i){if(height[i]==height[st.top()]){st.pop();st.push(i);}else if(height[i]<height[st.top()])st.push(i);else{while(!st.empty()&&height[i]>height[st.top()]){//有凹槽,top是中间int mid=st.top();st.pop();if(!st.empty()){//取栈顶,都要判断非空int h=min(height[i],height[st.top()])-height[mid];//高int w=i-st.top()-1;//宽count+=w*h;}}st.push(i);}}return count;}
};相等的情况pop()之前应该检查是否为空,但是初始和每一次循环结尾都有入栈操作,所以这里不用加。
简化。简化后的3个pop()操作都有可能遇栈空,所以都要加条件,否则报错:
class Solution {
public:int trap(vector<int>& height) {int n=height.size();int count=0;stack<int> st;st.push(0);for(int i=1;i<n;++i){while(!st.empty()&&height[i]>height[st.top()]){//有凹槽,top是中间int mid=st.top();st.pop();if(!st.empty()){//取栈顶,都要判断非空int h=min(height[i],height[st.top()])-height[mid];//高int w=i-st.top()-1;//宽count+=w*h;}}if(!st.empty()&&height[i]==height[st.top()]){st.pop();}st.push(i);}return count;}
};相关文章:

力扣● 503.下一个更大元素II ● 42. 接雨水
503.下一个更大元素II 与496.下一个更大元素 I的不同是要循环地搜索元素的下一个更大的数。那么主要是对于遍历结束后,单调栈里面剩下的那些元素。 如果直接把两个数组拼接在一起,然后使用单调栈求下一个最大值就可以。 代码实现的话,不用直…...

Java中的包装类
Java中的包装类 一、包装类是什么?二、对应关系:三、举例说明:Integer构造器:包装类特有的机制:自动装箱 自动拆箱常用方法 总结 一、包装类是什么? 以前定义变量,经常使用基本数据类型&#x…...

实时数仓的另一种构建方法starRocks的物化视图
一、 StarRocks是什么 StarRocks是一个分布式的、高性能的OLAP(联机分析处理)数据库,物化视图在StarRocks中具有重要作用。 二、 StarRocks物化视图能干啥 物化视图(Materialized Views)是数据库中的预先计算结果的存储。它们是由一个或多个基础表的聚合数据组成的,这…...

【PHP】通过PHP实时监控Apache、MySQL服务运行状态
一、前言 有些时候我们需要监控一些服务的运行状态,比如说Apach或MySQL的运行状态,最近工作中也开发了这方面的功能,记录下来怎样使用PHP语言来实时监控Apache、MySQL服务的运行状态。 如果想一键开启Apache或MySQL等其他服务可以看这篇文章…...
ETL的全量和增量模式
在当今信息爆炸的时代,数据管理已经成为各行各业必不可少的一环。而在数据管理中,全量与增量模式作为两种主要的策略,各自具有独特的优势和适用场景,巧妙地灵活运用二者不仅能提升数据处理效率,更能保障数据的准确性。…...

常用的IDE推荐
程序员在选择集成开发环境(IDE)时,会考虑多种因素,包括易用性、功能丰富性、性能以及是否支持他们正在使用的编程语言。以下是一些建议的IDE及其优点: 1.JetBrains PyCharm:专为Python开发而设计的IDE。 优…...
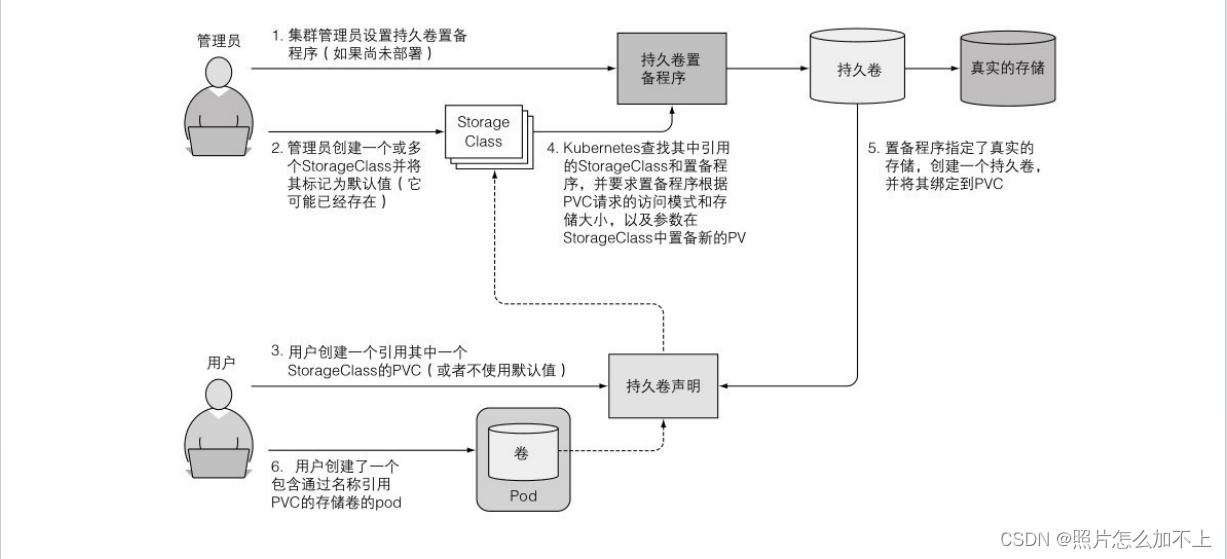
6、kubenetes 卷
1、什么是卷 在某些场景下,我们可能希望新的容器可以在之前容器结束的位 置继续运⾏,⽐如在物理机上重启进程。可能不需要(或者不想要) 整个⽂件系统被持久化,但又希望能保存实际数据的⽬录。 Kubernetes通过定义存储…...

前端学习笔记 | Node.js
一、Node.js入门 1、什么是Node.js 定义:是跨平台JS运行环境(可以独立执行JS的环境)作用: 编写数据接口,提供网页资源功能等等前端工程化:为后续学Vue和React等框架做铺垫 2、Node.js为何能执行JSÿ…...
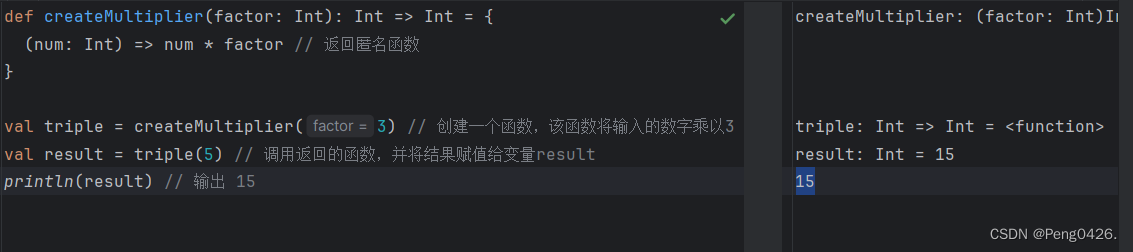
Spark-Scala语言实战(3)
在之前的文章中,我们学习了如何在来如何在IDEA离线和在线安装Scala,想了解的朋友可以查看这篇文章。同时,希望我的文章能帮助到你,如果觉得我的文章写的不错,请留下你宝贵的点赞,谢谢。 Spark-Scala语言实…...

diffusion model(十四): prompt-to-prompt 深度剖析
infopaperPrompt-to-Prompt Image Editing with Cross Attention Controlgithubhttps://github.com/google/prompt-to-promptOrg:Google Research个人复现https://github.com/myhz0606/diffusion_learning个人博客主页http://myhz0606.com/article/p2p 1 前言 基于扩散模型&a…...
)
线性表的顺序表示(顺序表)
静态分配: #include <stdbool.h> #include <stdio.h>typedef int ElementType;#define MaxSize 50 typedef struct {ElementType data[MaxSize];int length; }SqList;//初始化 //SqList L; void InitList(SqList L) {L.length 0; }//插入 bool ListIn…...

矩阵A的LU分解
文章目录 1. 矩阵的逆矩阵1.1 AB的逆矩阵1.2 转置矩阵 2. 2X2矩阵A消元3. 3X3矩阵A消元4. 运算量5. 置换矩阵-左行右列 本文主要目的是为了通过矩阵乘法实现矩阵A的分解。 1. 矩阵的逆矩阵 1.1 AB的逆矩阵 假设A,B矩阵都可逆 A ( B B − 1 ) A − 1 I (1) A(BB^{-1})A^{-1}…...

深入了解Flutter中Future的全部工厂方法及使用
在Flutter中,Future是一种表示异步操作结果的对象。它代表了一个可能已经完成或尚未完成的计算,可以用来处理异步任务。Flutter提供了多种工厂方法来创建Future对象,每种方法都有其特定的用途和优势。在本文中,我们将深入探讨Flut…...

python的BBS论坛系统flask-django-nodejs-php
为了更好地发挥本系统的技术优势,根据BBS论坛系统的需求,本文尝试以B/S架构设计模式中的django/flask框架,python语言为基础,通过必要的编码处理、BBS论坛系统整体框架、功能服务多样化和有效性的高级经验和技术实现方法ÿ…...
vulnhub-----pWnOS1.0靶机
文章目录 1.信息收集2.漏洞测试3.爆破hash4.提权 首先拿到一台靶机,就需要知道靶机的各种信息(IP地址,开放端口,有哪些目录,什么框架,cms是什么,网页有什么常见的漏洞,如sql注入&…...

vue 消息左右滚动(前后无缝衔接)
演示效果 封装的组件 <!--* Author:* Date: 2024-03-21 19:21:58* LastEditTime: 2024-03-21 20:31:50* LastEditors: Please set LastEditors* Description: 消息左右滚动 --> <template><divid"textScroll"class"text-scroll"mousemove&…...
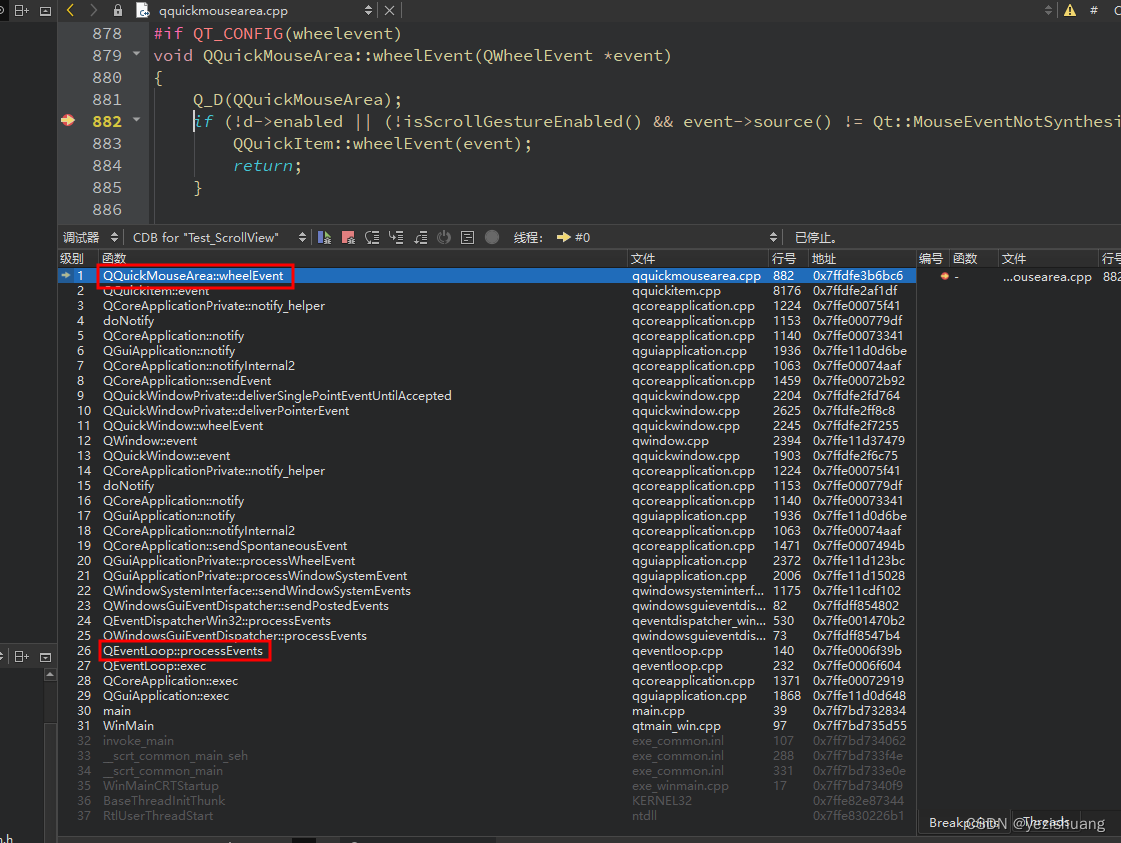
Qt如何直接处理系统事件(比如鼠标事件),而不是post事件
#include <QtGui/5.15.2/QtGui/qpa/qwindowsysteminterface.h> // 方便调试事件 QWindowSystemInterface::setSynchronousWindowSystemEvents(true); 直接再 qWindowsWndProc函数中处理 通常情况: 事件被放到一个队列中...

Web前端笔记+表单练习+五彩导航
一、笔记 表单:数据交互的一种方式 登录、注册、搜索 <from> <input type""> --- <input type"text"> --- 普通输入框,内容在一行显示 <input type"password"> --- 密码框 <input type"…...
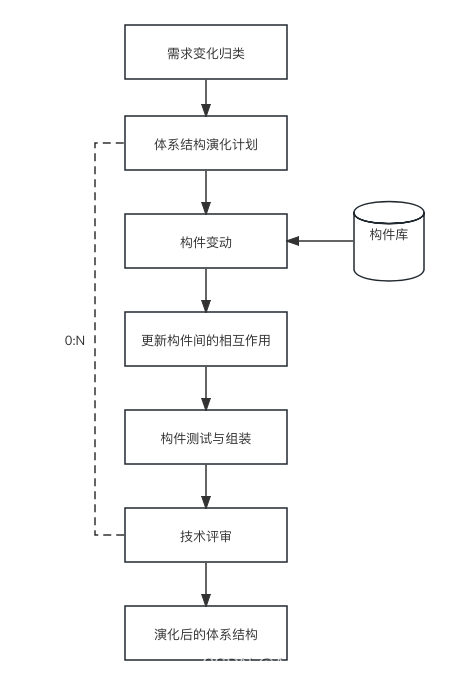
软件架构和基于架构的软件开发方法知识总结
一、软件架构定义 软件架构为软件系统提供了一个结构、行为和属性的高级抽象 软件架构是一种表达,使软件工程师能够: (1)分析设计在满足所规定的需求方面的有效性 (2)在设计变更相对容易的阶段,…...
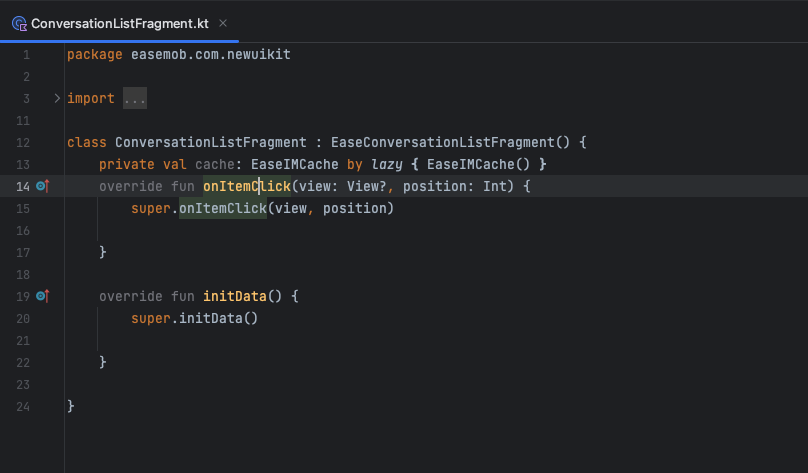
环信新版单群聊UIKit集成指南——Android篇
前言 环信新版UIKit已重磅发布!目前包含单群聊UIKit、聊天室ChatroomUIKit,本文详细讲解Android端单群聊UIKit的集成教程。 环信单群聊 UIKit 是基于环信即时通讯云 IM SDK 开发的一款即时通讯 UI 组件库,提供各种组件实现会话列表、聊天界…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
