深度强化学习(九)(改进策略梯度)

深度强化学习(九)(改进策略梯度)
一.带基线的策略梯度方法
Theorem:
设 b b b 是任意的函数, b b b与 A A A无关。把 b b b 作为动作价值函数 Q π ( S , A ) Q_\pi(S, A) Qπ(S,A) 的基线, 对策略梯度没有影响:
∇ θ J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ ( Q π ( S , A ) − b ) ⋅ ∇ θ ln π ( A ∣ S ; θ ) ] ] . \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})=\mathbb{E}_S\left[\mathbb{E}_{A \sim \pi(\cdot \mid S ; \boldsymbol{\theta})}\left[\left(Q_\pi(S, A)-b\right) \cdot \nabla_{\boldsymbol{\theta}} \ln \pi(A \mid S ; \boldsymbol{\theta})\right]\right] . ∇θJ(θ)=ES[EA∼π(⋅∣S;θ)[(Qπ(S,A)−b)⋅∇θlnπ(A∣S;θ)]].
proof:
E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ b ⋅ ∇ θ ln π ( A ∣ S ; θ ) ] ] = E A , S [ b ⋅ ∇ θ ln π ( A ∣ S ; θ ) ] = ∑ A , S b ⋅ ∇ θ π ( a ∣ s ; θ ) p ( a , s ) π ( a ∣ s ; θ ) = ∑ A , S b ⋅ ∇ θ π ( a ∣ s ; θ ) ⋅ p ( s ) = ∑ S [ b ⋅ p ( s ) ∑ A ∇ θ π ( a ∣ s ; θ ) ] = ∑ S [ b ⋅ p ( s ) ∇ θ ∑ A π ( a ∣ s ; θ ) ] = ∑ S [ b ⋅ p ( s ) ∇ θ 1 ] = 0 \begin{aligned} \Bbb E_{S}[\Bbb E_{A\sim\pi(\cdot\mid S;\boldsymbol \theta)}[b\cdot\nabla_{\boldsymbol \theta}\ln \pi(A\mid S;\boldsymbol \theta)]]&=\Bbb E_{A,S}[b\cdot \nabla_{\boldsymbol \theta}\ln \pi(A\mid S;\boldsymbol \theta)]\\ &=\sum_{A,S}b\cdot\nabla_{\boldsymbol \theta}\pi(a\mid s;\boldsymbol \theta)\frac{p(a,s)}{\pi(a\mid s;\boldsymbol \theta)}\\ &=\sum_{A,S}b\cdot\nabla_{\boldsymbol \theta}\pi(a\mid s;\boldsymbol \theta)\cdot p(s)\\ &=\sum_{S}[b\cdot p(s)\sum_{A}\nabla_{\boldsymbol \theta}\pi(a\mid s;\boldsymbol \theta)]\\ &=\sum_{S}[b\cdot p(s)\nabla_{\boldsymbol \theta}\sum_{A}\pi(a\mid s;\boldsymbol \theta)]\\ &=\sum_{S}[b\cdot p(s)\nabla_{\boldsymbol \theta}1]\\ &=0 \end{aligned} ES[EA∼π(⋅∣S;θ)[b⋅∇θlnπ(A∣S;θ)]]=EA,S[b⋅∇θlnπ(A∣S;θ)]=A,S∑b⋅∇θπ(a∣s;θ)π(a∣s;θ)p(a,s)=A,S∑b⋅∇θπ(a∣s;θ)⋅p(s)=S∑[b⋅p(s)A∑∇θπ(a∣s;θ)]=S∑[b⋅p(s)∇θA∑π(a∣s;θ)]=S∑[b⋅p(s)∇θ1]=0
所以策略梯度 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta}) ∇θJ(θ) 可以近似为下面的随机梯度:
g b ( s , a ; θ ) = [ Q π ( s , a ) − b ] ⋅ ∇ θ ln π ( a ∣ s ; θ ) \boldsymbol{g}_b(s, a ; \boldsymbol{\theta})=\left[Q_\pi(s, a)-b\right] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi(a \mid s ; \boldsymbol{\theta}) gb(s,a;θ)=[Qπ(s,a)−b]⋅∇θlnπ(a∣s;θ)
无论 b b b取何值, E A , S [ g b ( s , a ; θ ) ] \Bbb E_{A,S}[\boldsymbol g_{b}(s,a;\boldsymbol \theta)] EA,S[gb(s,a;θ)]都是策略梯度的无篇估计,但是随着 b b b取值的变化,方差会出现变化。
V a r = E A , S [ ( g b ( S , A ; θ ) − ∇ θ J ( θ ) ) 2 ] = E A , S [ g b ( S , A ; θ ) 2 ] − [ ∇ θ J ( θ ) ] 2 = E A , S [ ( Q π ( S , A ) − b ) 2 ∇ θ 2 ln π ( A ∣ S ; θ ) ] − [ ∇ θ J ( θ ) ] 2 \begin{aligned} \Bbb{Var}&=\Bbb E_{A,S}[(\boldsymbol{g}_b(S, A ; \boldsymbol{\theta})-\nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta}))^2]\\ &=\Bbb E_{A,S}[\boldsymbol{g}_b(S, A ; \boldsymbol{\theta})^2]-[\nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})]^2\\ &=\Bbb E_{A,S}[(Q_{\pi}(S,A)-b)^2\nabla_{\boldsymbol{\theta}}^2\ln \pi(A\mid S;\boldsymbol{\theta})]-[\nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})]^2\\ \end{aligned} Var=EA,S[(gb(S,A;θ)−∇θJ(θ))2]=EA,S[gb(S,A;θ)2]−[∇θJ(θ)]2=EA,S[(Qπ(S,A)−b)2∇θ2lnπ(A∣S;θ)]−[∇θJ(θ)]2
由于 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta}) ∇θJ(θ)是与 b b b无关的常数,所以仅需极小化 E A , S [ ( Q π ( S , A ) − b ) 2 ∇ θ 2 ln π ( A ∣ S ; θ ) ] \Bbb E_{A,S}[(Q_{\pi}(S,A)-b)^2\nabla_{\boldsymbol{\theta}}^2\ln \pi(A\mid S;\boldsymbol{\theta})] EA,S[(Qπ(S,A)−b)2∇θ2lnπ(A∣S;θ)]
E A , S [ ( Q π ( S , A ) − b ) 2 ∇ θ 2 ln π ( A ∣ S ; θ ) ] = E S [ E A ∼ π ( A ∣ S ; θ ) [ ( Q π ( S , A ) − b ) 2 ∇ θ 2 ln π ( A ∣ S ; θ ) ] ] = E S [ E A ∼ ∇ θ 2 π ( A ∣ S ; θ ) π ( A ∣ S ; θ ) [ ( Q π ( S , A ) − b ) 2 ] ] \begin{aligned} \Bbb E_{A,S}[(Q_{\pi}(S,A)-b)^2\nabla_{\boldsymbol{\theta}}^2\ln \pi(A\mid S;\boldsymbol{\theta})]&=\Bbb E_{S}[\Bbb E_{A\sim \pi(A\mid S;\boldsymbol \theta)}[(Q_{\pi}(S,A)-b)^2\nabla_{\boldsymbol \theta}^2\ln\pi(A\mid S;\boldsymbol \theta)]]\\ &=\Bbb E_{S}[\Bbb E_{A\sim \frac{\nabla_{\boldsymbol \theta}^2\pi(A\mid S;\boldsymbol \theta)}{\pi(A\mid S;\boldsymbol \theta)}}[(Q_{\pi}(S,A)-b)^2]] \end{aligned} EA,S[(Qπ(S,A)−b)2∇θ2lnπ(A∣S;θ)]=ES[EA∼π(A∣S;θ)[(Qπ(S,A)−b)2∇θ2lnπ(A∣S;θ)]]=ES[EA∼π(A∣S;θ)∇θ2π(A∣S;θ)[(Qπ(S,A)−b)2]]
所以要最小化方差,令 A ∼ ∇ θ 2 π ( A ∣ S ; θ ) π ( A ∣ S ; θ ) A\sim \frac{\nabla_{\boldsymbol \theta}^2\pi(A\mid S;\boldsymbol \theta)}{\pi(A\mid S;\boldsymbol \theta)} A∼π(A∣S;θ)∇θ2π(A∣S;θ)为N-K密度,则
b = E A ∼ ∇ θ 2 π ( A ∣ S ; θ ) π ( A ∣ S ; θ ) [ Q π ( S , A ) ] / E A ∼ ∇ θ 2 π ( A ∣ S ; θ ) π ( A ∣ S ; θ ) [ ] = E A ∼ π θ [ ∇ θ log π θ ( A ∣ S ) T ∇ θ log π ( A ∣ S ) Q ( S , A ) ] E A ∼ π θ [ ∇ θ log π θ ( A ∣ S ) T ∇ θ log π θ ( A ∣ S ) ] \begin{aligned} b&=\Bbb E_{A\sim \frac{\nabla_{\boldsymbol \theta}^2\pi(A\mid S;\boldsymbol \theta)}{\pi(A\mid S;\boldsymbol \theta)}}[Q_{\pi}(S,A)]/\Bbb E_{A \sim \frac{\nabla_{\boldsymbol \theta}^2\pi(A\mid S;\boldsymbol \theta)}{\pi(A\mid S;\boldsymbol \theta)}}[]\\ &=\frac{\mathbb{E}_{A \sim \pi_\theta}\left[\nabla_\theta \log \pi_\theta(A \mid S)^T \nabla_\theta \log \pi(A \mid S) Q(S, A)\right]}{\mathbb{E}_{A \sim \pi_\theta}\left[\nabla_\theta \log \pi_\theta(A \mid S)^T \nabla_\theta \log \pi_\theta(A \mid S)\right]} \end{aligned} b=EA∼π(A∣S;θ)∇θ2π(A∣S;θ)[Qπ(S,A)]/EA∼π(A∣S;θ)∇θ2π(A∣S;θ)[]=EA∼πθ[∇θlogπθ(A∣S)T∇θlogπθ(A∣S)]EA∼πθ[∇θlogπθ(A∣S)T∇θlogπ(A∣S)Q(S,A)]
,我们使用 b = E A ∼ π ( A ∣ S ) [ Q π ( S , A ) ] = V π ( S ) b=\Bbb E_{A\sim \pi(A\mid S)}[Q_{\pi}(S,A)]=V_\pi(S) b=EA∼π(A∣S)[Qπ(S,A)]=Vπ(S)作为近似代替。
我们使用状态价值 V π ( s ) V_\pi(s) Vπ(s) 作基线,得到策略梯度的一个无偏估计:
g ( s , a ; θ ) = [ Q π ( s , a ) − V π ( s ) ] ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boldsymbol{g}(s, a ; \boldsymbol{\theta})=\left[Q_\pi(s, a)-V_\pi(s)\right] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi(a \mid s ; \boldsymbol{\theta}) . g(s,a;θ)=[Qπ(s,a)−Vπ(s)]⋅∇θlnπ(a∣s;θ).
REINFORCE使用实际观测的回报 u u u 来代替动作价值 Q π ( s , a ) Q_\pi(s, a) Qπ(s,a) 。此处我们同样用 u u u 代替 Q π ( s , a ) Q_\pi(s, a) Qπ(s,a) 。此外, 我们还用一个神经网络 v ( s ; w ) v(s ; \boldsymbol{w}) v(s;w) 近似状态价值函数 V π ( s ) V_\pi(s) Vπ(s) 。这样一来, g ( s , a ; θ ) \boldsymbol{g}(s, a ; \boldsymbol{\theta}) g(s,a;θ) 就被近似成了:
g ~ ( s , a ; θ ) = [ u − v ( s ; w ) ] ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \tilde{\boldsymbol{g}}(s, a ; \boldsymbol{\theta})=[u-v(s ; \boldsymbol{w})] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi(a \mid s ; \boldsymbol{\theta}) . g~(s,a;θ)=[u−v(s;w)]⋅∇θlnπ(a∣s;θ).
可以用 g ~ ( s , a ; θ ) \tilde{\boldsymbol{g}}(s, a ; \boldsymbol{\theta}) g~(s,a;θ) 作为策略梯度 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta}) ∇θJ(θ) 的近似, 更新策略网络参数:
θ ← θ + β ⋅ g ~ ( s , a ; θ ) \boldsymbol{\theta} \leftarrow \boldsymbol{\theta}+\beta \cdot \tilde{\boldsymbol{g}}(s, a ; \boldsymbol{\theta}) θ←θ+β⋅g~(s,a;θ)
训练价值网络的方法是回归 (regression)。回忆一下, 状态价值是回报的期望:
V π ( s t ) = E [ U t ∣ S t = s t ] , V_\pi\left(s_t\right)=\mathbb{E}\left[U_t \mid S_t=s_t\right], Vπ(st)=E[Ut∣St=st],
期望消掉了动作 A t , A t + 1 , ⋯ , A n A_t, A_{t+1}, \cdots, A_n At,At+1,⋯,An 和状态 S t + 1 , ⋯ , S n S_{t+1}, \cdots, S_n St+1,⋯,Sn 训练价值网络的目的是让 v ( s t ; w ) v\left(s_t ; \boldsymbol{w}\right) v(st;w)拟合 V π ( s t ) V_\pi\left(s_t\right) Vπ(st), 即拟合 u t u_t ut 的期望。定义
损失失函数:
L ( w ) = 1 2 n ∑ t = 1 n [ v ( s t ; w ) − u t ] 2 . L(\boldsymbol{w})=\frac{1}{2 n} \sum_{t=1}^n\left[v\left(s_t ; \boldsymbol{w}\right)-u_t\right]^2 . L(w)=2n1t=1∑n[v(st;w)−ut]2.
设 v ^ t = v ( s t ; w ) \widehat{v}_t=v\left(s_t ; \boldsymbol{w}\right) v t=v(st;w) 。损失函数的梯度是:
∇ w L ( w ) = 1 n ∑ t = 1 n ( v ^ t − u t ) ⋅ ∇ w v ( s t ; w ) . \nabla_{\boldsymbol{w}} L(\boldsymbol{w})=\frac{1}{n} \sum_{t=1}^n\left(\widehat{v}_t-u_t\right) \cdot \nabla_{\boldsymbol{w}} v\left(s_t ; \boldsymbol{w}\right) . ∇wL(w)=n1t=1∑n(v t−ut)⋅∇wv(st;w).
做一次梯度下降更新 w \boldsymbol{w} w :
w ← w − α ⋅ ∇ w L ( w ) . \boldsymbol{w} \leftarrow \boldsymbol{w}-\alpha \cdot \nabla_{\boldsymbol{w}} L(\boldsymbol{w}) . w←w−α⋅∇wL(w).
接下来的训练过程与 r e i n f o r c e reinforce reinforce一样。
二.Advantage Actor-Critic (A2C)
训练价值网络:reinforce使用蒙特卡洛方法直接求出了所有 u t u_t ut,从而可以直接训练 v π ( s ) v_{\pi}(s) vπ(s)而在 a c t o r − c r i t i c actor-critic actor−critic中并未使用蒙特卡洛方法,我们依据贝尔曼方程进行自举训练。
V π ( s t ) = E A t , S t + 1 [ R t + γ ⋅ V π ( S t + 1 ) ∣ S t = s t ] = E A t [ E S t + 1 [ R t + γ ⋅ V π ( S t + 1 ) ∣ S t = s t , A t ] ∣ S t = s t ] \begin{aligned} V_\pi\left(s_t\right)&=\mathbb{E}_{A_t, S_{t+1}}\left[R_t+\gamma \cdot V_\pi\left(S_{t+1}\right) \mid S_t=s_t\right]\\ &= \Bbb E_{A_t}[\Bbb E_{S_{t+1}}[R_{t}+\gamma \cdot V_{\pi}(S_{t+1})\mid S_t=s_t,A_t] \mid S_t=s_t] \end{aligned} Vπ(st)=EAt,St+1[Rt+γ⋅Vπ(St+1)∣St=st]=EAt[ESt+1[Rt+γ⋅Vπ(St+1)∣St=st,At]∣St=st]
从初始状态 s t s_t st出发,依据策略 π ( A ∣ S ) \pi(A\mid S) π(A∣S)选取动作 a t a_t at,再依据状态转移概率 p ( S t + 1 ∣ A t , S t ) p(S_{t+1}\mid A_t,S_t) p(St+1∣At,St),选中下一刻状态 s t + 1 s_{t+1} st+1,得出 r t r_{t} rt.
则 y t = r t + v π ( s t + 1 ; w ) y_t=r_t+v_{\pi}(s_{t+1};\boldsymbol{w}) yt=rt+vπ(st+1;w)
具体这样更新价值网络参数 w \boldsymbol{w} w 。定义损失函数
L ( w ) ≜ 1 2 [ v ( s t ; w ) − y t ^ ] 2 . L(\boldsymbol{w}) \triangleq \frac{1}{2}\left[v\left(s_t ; \boldsymbol{w}\right)-\widehat{y_t}\right]^2 . L(w)≜21[v(st;w)−yt ]2.
设 v ^ t ≜ v ( s t ; w ) \widehat{v}_t \triangleq v\left(s_t ; \boldsymbol{w}\right) v t≜v(st;w) 。损失函数的梯度是:
∇ w L ( w ) = ( v ^ t − y ^ t ) ⏟ TD 误差 δ t ⋅ ∇ w v ( s t ; w ) . \nabla_{\boldsymbol{w}} L(\boldsymbol{w})=\underbrace{\left(\widehat{v}_t-\widehat{y}_t\right)}_{\text {TD 误差 } \delta_t} \cdot \nabla_{\boldsymbol{w}} v\left(s_t ; \boldsymbol{w}\right) . ∇wL(w)=TD 误差 δt (v t−y t)⋅∇wv(st;w).
定义 TD 误差为 δ t ≜ v ^ t − y ^ t \delta_t \triangleq \widehat{v}_t-\widehat{y}_t δt≜v t−y t 。做一轮梯度下降更新 w : \boldsymbol{w}: w:
w ← w − α ⋅ δ t ⋅ ∇ w v ( s t ; w ) . \boldsymbol{w} \leftarrow \boldsymbol{w}-\alpha \cdot \delta_t \cdot \nabla_{\boldsymbol{w}} v\left(s_t ; \boldsymbol{w}\right) . w←w−α⋅δt⋅∇wv(st;w).
训练策略网络:贝尔曼公式:
Q π ( s t , a t ) = E S t + 1 ∼ p ( ⋅ ∣ s t , a t ) [ R t + γ ⋅ V π ( S t + 1 ) ] . Q_\pi\left(s_t, a_t\right)=\mathbb{E}_{S_{t+1} \sim p\left(\cdot \mid s_t, a_t\right)}\left[R_t+\gamma \cdot V_\pi\left(S_{t+1}\right)\right] . Qπ(st,at)=ESt+1∼p(⋅∣st,at)[Rt+γ⋅Vπ(St+1)].
把近似策略梯度 g ( s t , a t ; θ ) \boldsymbol{g}\left(s_t, a_t ; \boldsymbol{\theta}\right) g(st,at;θ) 中的 Q π ( s t , a t ) Q_\pi\left(s_t, a_t\right) Qπ(st,at) 替换成上面的期望, 得到:
g ( s t , a t ; θ ) = [ Q π ( s t , a t ) − V π ( s t ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) = [ E S t + 1 [ R t + γ ⋅ V π ( S t + 1 ) ] − V π ( s t ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \begin{aligned} \boldsymbol{g}\left(s_t, a_t ; \boldsymbol{\theta}\right) & =\left[Q_\pi\left(s_t, a_t\right)-V_\pi\left(s_t\right)\right] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi\left(a_t \mid s_t ; \boldsymbol{\theta}\right) \\ & =\left[\mathbb{E}_{S_{t+1}}\left[R_t+\gamma \cdot V_\pi\left(S_{t+1}\right)\right]-V_\pi\left(s_t\right)\right] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi\left(a_t \mid s_t ; \boldsymbol{\theta}\right) . \end{aligned} g(st,at;θ)=[Qπ(st,at)−Vπ(st)]⋅∇θlnπ(at∣st;θ)=[ESt+1[Rt+γ⋅Vπ(St+1)]−Vπ(st)]⋅∇θlnπ(at∣st;θ).
当智能体执行动作 a t a_t at 之后, 环境给出新的状态 s t + 1 s_{t+1} st+1 和奖励 r t r_t rt; 利用 s t + 1 s_{t+1} st+1 和 r t r_t rt 对上面的期望做蒙特卡洛近似, 得到:
g ( s t , a t ; θ ) ≈ [ r t + γ ⋅ V π ( s t + 1 ) − V π ( s t ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \boldsymbol{g}\left(s_t, a_t ; \boldsymbol{\theta}\right) \approx\left[r_t+\gamma \cdot V_\pi\left(s_{t+1}\right)-V_\pi\left(s_t\right)\right] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi\left(a_t \mid s_t ; \boldsymbol{\theta}\right) . g(st,at;θ)≈[rt+γ⋅Vπ(st+1)−Vπ(st)]⋅∇θlnπ(at∣st;θ).
进一步把状态价值函数 V π ( s ) V_\pi(s) Vπ(s) 替换成价值网络 v ( s ; w ) v(s ; \boldsymbol{w}) v(s;w), 得到:
g ~ ( s t , a t ; θ ) ≜ [ r t + γ ⋅ v ( s t + 1 ; w ) ⏟ T D 目标 y ^ t − v ( s t ; w ) ] ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) \tilde{\boldsymbol{g}}\left(s_t, a_t ; \boldsymbol{\theta}\right) \triangleq[\underbrace{r_t+\gamma \cdot v\left(s_{t+1} ; \boldsymbol{w}\right)}_{\mathrm{TD} \text { 目标 } \hat{y}_t}-v\left(s_t ; \boldsymbol{w}\right)] \cdot \nabla_{\boldsymbol{\theta}} \ln \pi\left(a_t \mid s_t ; \boldsymbol{\theta}\right) g~(st,at;θ)≜[TD 目标 y^t rt+γ⋅v(st+1;w)−v(st;w)]⋅∇θlnπ(at∣st;θ)
前面定义了 TD 目标和 TD 误差:
y ^ t ≜ r t + γ ⋅ v ( s t + 1 ; w ) 和 δ t ≜ v ( s t ; w ) − y ^ t . \widehat{y}_t \triangleq r_t+\gamma \cdot v\left(s_{t+1} ; \boldsymbol{w}\right) \quad \text { 和 } \quad \delta_t \triangleq v\left(s_t ; \boldsymbol{w}\right)-\widehat{y}_t . y t≜rt+γ⋅v(st+1;w) 和 δt≜v(st;w)−y t.
因此, 可以把 g ~ \tilde{\boldsymbol{g}} g~ 写成:
g ~ ( s t , a t ; θ ) ≜ − δ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) . \tilde{\boldsymbol{g}}\left(s_t, a_t ; \boldsymbol{\theta}\right) \triangleq-\delta_t \cdot \nabla_{\boldsymbol{\theta}} \ln \pi\left(a_t \mid s_t ; \boldsymbol{\theta}\right) . g~(st,at;θ)≜−δt⋅∇θlnπ(at∣st;θ).
g ~ \tilde{\boldsymbol{g}} g~ 是 g \boldsymbol{g} g 的近似,所以也是策略梯度 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta}) ∇θJ(θ) 的近似。用 g ~ \tilde{\boldsymbol{g}} g~ 更新策略网络参数 θ \boldsymbol{\theta} θ :
θ ← θ + β ⋅ g ~ ( s t , a t ; θ ) . \boldsymbol{\theta} \leftarrow \boldsymbol{\theta}+\beta \cdot \tilde{\boldsymbol{g}}\left(s_t, a_t ; \boldsymbol{\theta}\right) . θ←θ+β⋅g~(st,at;θ).
训练流程。设当前策略网络参数是 θ now \boldsymbol{\theta}_{\text {now }} θnow , 价值网络参数是 w now \boldsymbol{w}_{\text {now }} wnow 。执行下面的步骤, 将参数更新成 θ new \theta_{\text {new }} θnew 和 w new \boldsymbol{w}_{\text {new }} wnew :
- 观测到当前状态 s t s_t st, 根据策略网络做决策: a t ∼ π ( ⋅ ∣ s t ; θ now ) a_t \sim \pi\left(\cdot \mid s_t ; \boldsymbol{\theta}_{\text {now }}\right) at∼π(⋅∣st;θnow ), 并让智能体执行动作 a t a_t at 。
- 从环境中观测到奖励 r t r_t rt 和新的状态 s t + 1 s_{t+1} st+1 。
- 让价值网络打分:
v ^ t = v ( s t ; w now ) 和 v ^ t + 1 = v ( s t + 1 ; w now ) \widehat{v}_t=v\left(s_t ; \boldsymbol{w}_{\text {now }}\right) \quad \text { 和 } \quad \widehat{v}_{t+1}=v\left(s_{t+1} ; \boldsymbol{w}_{\text {now }}\right) v t=v(st;wnow ) 和 v t+1=v(st+1;wnow ) - 计算 TD 目标和 TD 误差:
y ^ t = r t + γ ⋅ v ^ t + 1 和 δ t = v ^ t − y ^ t . \widehat{y}_t=r_t+\gamma \cdot \widehat{v}_{t+1} \quad \text { 和 } \quad \delta_t=\widehat{v}_t-\widehat{y}_t . y t=rt+γ⋅v t+1 和 δt=v t−y t. - 更新价值网络:
w new ← w now − α ⋅ δ t ⋅ ∇ w v ( s t ; w now ) . \boldsymbol{w}_{\text {new }} \leftarrow \boldsymbol{w}_{\text {now }}-\alpha \cdot \delta_t \cdot \nabla_{\boldsymbol{w}} v\left(s_t ; \boldsymbol{w}_{\text {now }}\right) . wnew ←wnow −α⋅δt⋅∇wv(st;wnow ). - 更新策略网络:
θ new ← θ now − β ⋅ δ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ now ) . \boldsymbol{\theta}_{\text {new }} \leftarrow \boldsymbol{\theta}_{\text {now }}-\beta \cdot \delta_t \cdot \nabla_{\boldsymbol{\theta}} \ln \pi\left(a_t \mid s_t ; \boldsymbol{\theta}_{\text {now }}\right) . θnew ←θnow −β⋅δt⋅∇θlnπ(at∣st;θnow ).
相关文章:

深度强化学习(九)(改进策略梯度)
深度强化学习(九)(改进策略梯度) 一.带基线的策略梯度方法 Theorem: 设 b b b 是任意的函数, b b b与 A A A无关。把 b b b 作为动作价值函数 Q π ( S , A ) Q_\pi(S, A) Qπ(S,A) 的基线, 对策略梯度没有影响: ∇ θ J …...

Oracle修改Number类型精度报错:ORA-01440
修改Number类型的字段的精度SQL ALTER TABLE XXXX MODIFY RATE NUMBER(30,6); 如果表已经存在数据,报错信息如下: ORA-01440: column to be modified must be empty to decrease precision or scale 废话不多说,解决方案如下:…...

美团到店-后端开发一面
1. 介绍一下spring的两大核心思想 2. 介绍一下java的代理,以及动态代理和静态代理的区别 3. spring动态代理是如何生成的,jdk动态代理和cglib的区别 4. 介绍一下synchronized关键字、以及synchronized锁和lock的区别 5. 讲一下java中synchronized的锁升级…...

面试算法-77-括号生成
题目 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”] 解 class Solution {publ…...

webpack5零基础入门-12搭建开发服务器
1.目的 每次写完代码都需要手动输入指令才能编译代码,太麻烦了,我们希望一切自动化 2.安装相关包 npm install --save-dev webpack-dev-server 3.添加配置 在webpack.config.js中添加devServer相关配置 /**开发服务器 */devServer: {host: localhos…...

opengl日记10-opengl使用多个纹理示例
文章目录 环境代码CMakeLists.txt文件内容不变。fragmentShaderSource.fsvertexShaderSource.vsmain.cpp 总结 环境 系统:ubuntu20.04opengl版本:4.6glfw版本:3.3glad版本:4.6cmake版本:3.16.3gcc版本:10.…...
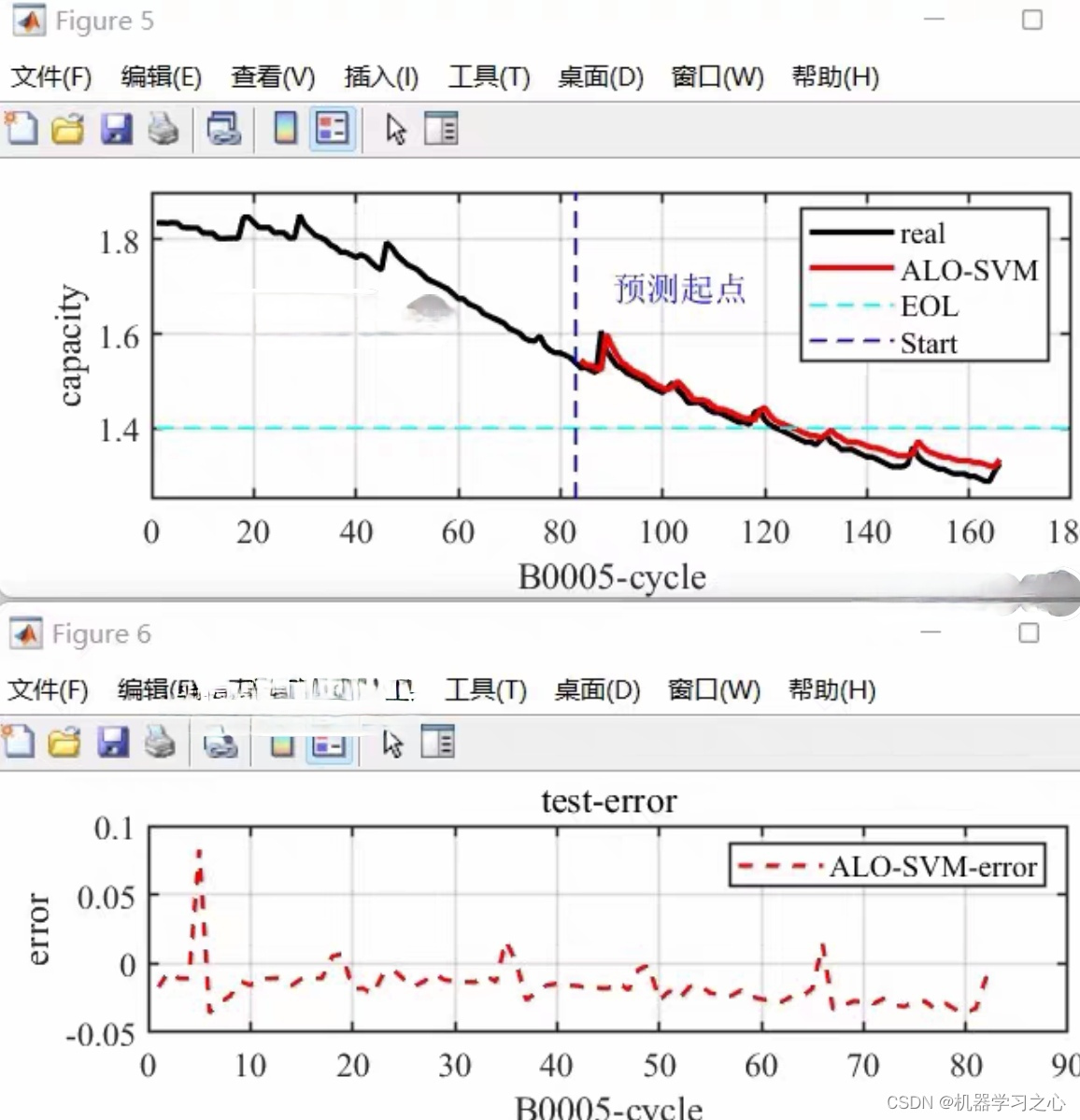
锂电池寿命预测 | Matlab基于ALO-SVR蚁狮优化支持向量回归的锂离子电池剩余寿命预测
目录 预测效果基本介绍程序设计参考资料 预测效果 基本介绍 锂电池寿命预测 | Matlab基于ALO-SVR蚁狮优化支持向量回归的锂离子电池剩余寿命预测 基于蚁狮优化和支持向量回归的锂离子电池剩余寿命预测: 1、提取NASA数据集的电池容量,以历史容量作为输入,…...

动态规划15 | ● 392.判断子序列 ● *115.不同的子序列
392.判断子序列 https://programmercarl.com/0392.%E5%88%A4%E6%96%AD%E5%AD%90%E5%BA%8F%E5%88%97.html 考点 子序列问题 我的思路 dp[i][j]的含义是,两个序列分别取到下标为i和j的时候,他们是否满足前者是后者的子序列,满足为True&#x…...

APP UI自动化测试思路总结
首先想要说明一下,APP自动化测试可能很多公司不用,但也是大部分自动化测试工程师、高级测试工程师岗位招聘信息上要求的,所以为了更好的待遇,我们还是需要花时间去掌握的,毕竟谁也不会跟钱过不去。 接下来,…...
)
Codeforces Round 936 (Div. 2)
C. Tree Cutting 题意:给定一棵树,需要删除 k 条边,使得 k1 个联通块中的最小结点数最大。求出这个最大值 思路:求最小值最大--想到二分答案--然后深搜满足条件的连通块是否大于k即可 #include<iostream> #include<al…...
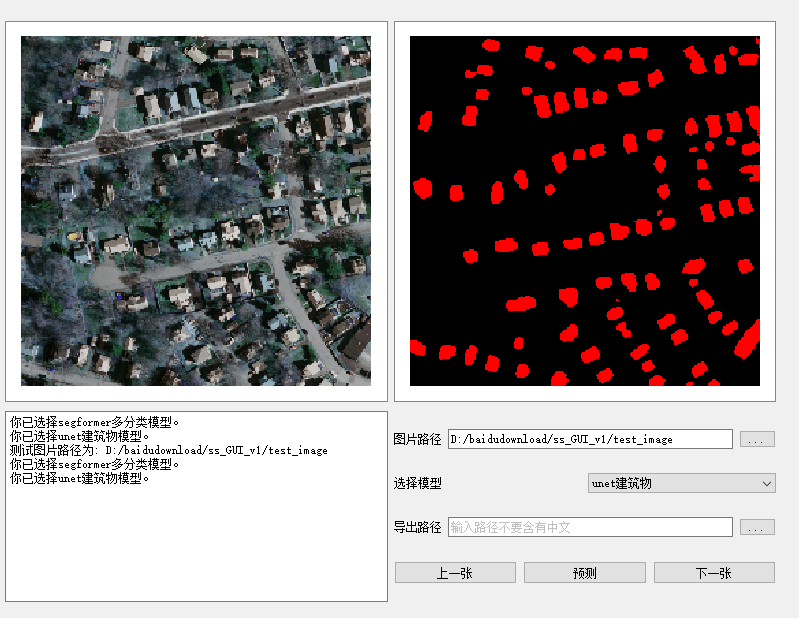
yolov6实现遥感影像目标识别|以DIOR数据集为例
1 目标检测是计算机视觉领域中的一项重要任务,它的目标是在图像或视频中检测出物体的位置和类别。YOLO(You Only Look Once)是一系列经典的目标检测算法,最初由Joseph Redmon等人于2016年提出。YOLO算法具有快速、简单、端到端的特…...

stable-diffusion-electron-clickstart 支持windows AMD显卡
前言 使用vue3 vite electron element-plus构建,正好学习下electrongithub stable-diffusion “画境导航者” 启动器 简介 stable-diffusion “画境导航者” 启动器支持功能 一键启动打开文件夹(tmp、txt2img-images)等模型所在文件夹&…...

ES进程除了kill之外,有什么优雅关闭的方式吗?
问题 Linux环境中,Elasticsearch 8的进程除了kill之外,有什么优雅关闭的方式吗? 具体实施方式 在Linux环境中,Elasticsearch(ES)进程可以通过多种方式实现优雅关闭,这种方式允许它完成必要的…...
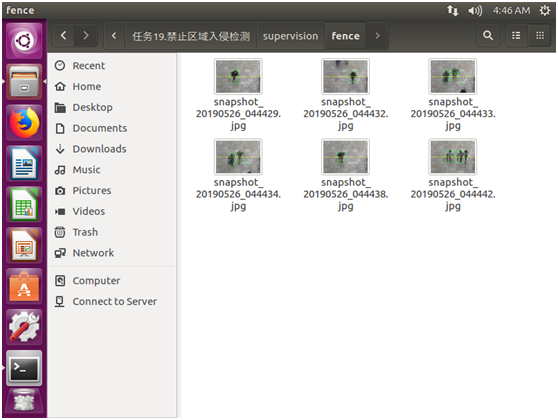
院子摄像头的监控
院子摄像头的监控和禁止区域入侵检测相比,多了2个功能:1)如果检测到有人入侵,则把截图保存起来,2)如果检测到有人入侵,则向数据库插入一条事件数据。 打开checkingfence.py,添加如下…...

SpringBoot3使用响应Result类返回的响应状态码为406
Resolved [org.springframework.web.HttpMediaTypeNotAcceptableException: No acceptable representation] 解决方法:Result类上加上Data注解...
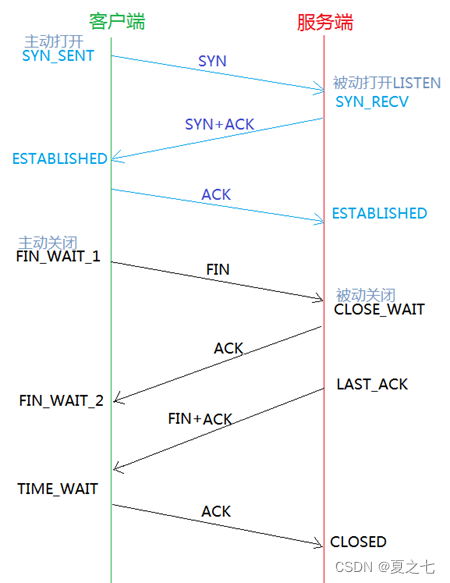
基础:TCP四次挥手做了什么,为什么要挥手?
1. TCP 四次挥手在做些什么 1. 第一次挥手 : 1)挥手作用:主机1发送指令告诉主机2,我没有数据发送给你了。 2)数据处理:主机1(可以是客户端,也可以是服务端),…...

Android Studio实现内容丰富的安卓校园二手交易平台(带聊天功能)
获取源码请点击文章末尾QQ名片联系,源码不免费,尊重创作,尊重劳动 项目编号083 1.开发环境android stuido jdk1.8 eclipse mysql tomcat 2.功能介绍 安卓端: 1.注册登录 2.查看二手商品列表 3.发布二手商品 4.商品详情 5.聊天功能…...

第十一届蓝桥杯省赛第一场真题
2065. 整除序列 - AcWing题库 #include <bits/stdc.h> using namespace std; #define int long long//记得开long long void solve(){int n;cin>>n;while(n){cout<<n<< ;n/2;} } signed main(){int t1;while(t--)solve();return 0; } 2066. 解码 - …...
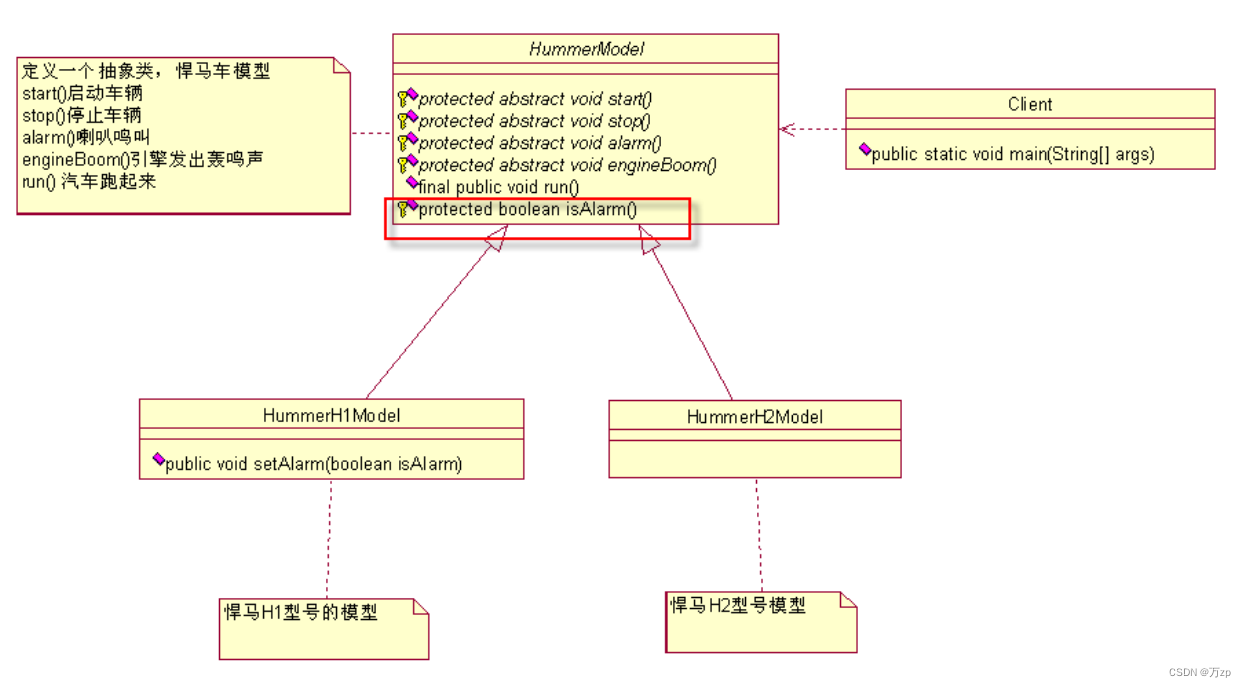
设计模式 模板方法模式
01.如果接到一个任务,要求设计不同型号的悍马车 02.设计一个悍马车的抽象类(模具,车模) public abstract class HummerModel {/** 首先,这个模型要能够被发动起来,别管是手摇发动,还是电力发动…...
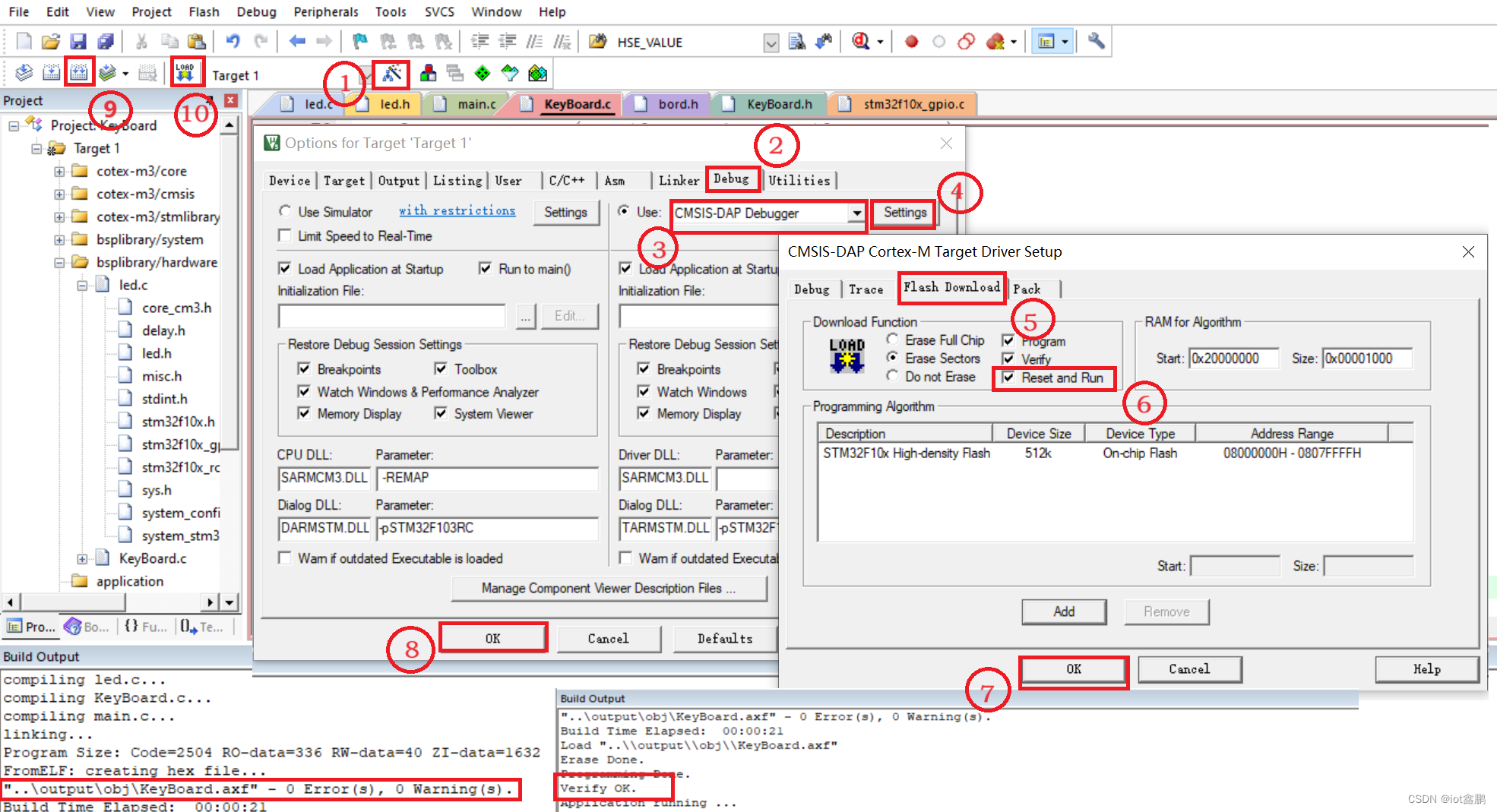
【STM32嵌入式系统设计与开发】——6矩阵按键应用(4x4)
这里写目录标题 一、任务描述二、任务实施1、SingleKey工程文件夹创建2、函数编辑(1)主函数编辑(2)LED IO初始化函数(LED_Init())(3)开发板矩阵键盘IO初始化(ExpKeyBordInit())&…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
