把本地代码初始化到远程git仓库
本地代码,推送到远程的git仓库。
第一种方法
第一步:建立远程的git仓库
第二步:拉取git仓库到本地
第三步:将本地代码复制到本地的git拉下来的文件夹中
第四步:代码提交即可
git add . --> git commit -m 初始化 --> git push
第二种方法
第一步:建立远程的git仓库
第二步:
输入git add . 这个是将项目上所有的文件添加到仓库中的意思,如果想添加某个特定的文件,只需把.换成这个特定的文件名即可。
我是使用了".",把整个文件夹下信息都提交了。
第三步:输入git commit -m "first commit",表示你对这次提交的注释,双引号里面的内容可以根据个人的需要改。指的是当前提交说明
第四步:输入git remote add origin https://自己的仓库url地址(这个url可以到自己的git中创建的仓库页面找就是最上面一个输入栏中的url) 将本地的仓库关联到github上,
最后一步,输入git push -u origin master,这是把代码上传到github仓库的意思。
执行完后,如果没有异常,会等待几秒,然后跳出一个让你输入Username和Password 的窗口,你只要输人github的登录账号和密码就行了。
问题
1:
You are in 'detached HEAD' state, which means that you're not on any branch Checkout a branch to make update possible.
解决:切换到你的工作分支即可,命令如下:git checkout XXXX(分支名)
2:hint: Updates were rejected because a pushed branch tip is behind its remote
解决:强推 git push --force-with-lease origin 本地分支名:远端分支名
3:git pull 提示错误 fatal: refusing to merge unrelated histories
解决:在git pull 命令中添 --allow-unrelated-histories
在实际使用中还会遇到各种各样的问题和各种坑,希望大家补充
相关文章:

把本地代码初始化到远程git仓库
本地代码,推送到远程的git仓库。第一种方法第一步:建立远程的git仓库第二步:拉取git仓库到本地第三步:将本地代码复制到本地的git拉下来的文件夹中第四步:代码提交即可git add . --> git commit -m 初始化 --> g…...

关于angular中的生命周期函数
生命周期函数,也叫生命周期钩子。 Angular的每个组件(包括根组件和子组件)都存在一个生命周期,从创建、更新、到销毁,Angular提供组件生命周期钩子函数, 组件的生命周期从实例化组件类并渲染组件视图及其…...

【拼图】拼图游戏-微信小程序开发流程详解
还记得小时候玩过的经典拼图游戏吗,上小学时,在路边摊用买个玩具,是一个正方形盒子形状,里面装的是图片分割成的很多块,还差一块,怎么描述好呢,和魔方玩具差不多,有没有听说叫二维的…...
)
第六章 opengl之光照(颜色)
OpenGL光照颜色创建一个光照场景光照 颜色 颜色由RGB组成,分别是红色,绿色,蓝色。举例定义一个颜色向量: glm::vec3 coral(1.0f, 0.5f, 0.31f);而在现实中,人眼看到的是 物体反射后的颜色,也就是说不能被…...

C语言-基础了解-19-C位域
C位域 一、C位域 如果程序的结构中包含多个开关量,只有 TRUE/FALSE 变量,如下: struct {unsigned int widthValidated;unsigned int heightValidated; } status;这种结构需要 8 字节的内存空间,但在实际上,在每个变…...

MapReduce全排序和二次排序
排序是MapReduce框架中最重要的操作之一。MapTask和ReduceTask均会对数据按照key进行排序。该操作属于Hadoop的默认行为。任何应用程序中的数据均会被排序,而不管逻辑上是否需要。默认排序是按照字典顺序排序,且实现该排序的方法是快速排序。对于MapTask…...

【Vue3】封装数字框组件
数量选择组件-基本结构 (1)准备基本结构 <script lang"ts" setup name"Numbox"> // </script> <template><div class"numbox"><div class"label">数量</div><div cla…...

C++-简述strcpy、sprintf 和 memcpy 的区别
回答如下: strcpy 函数:用于将一个字符串(以 NULL 结尾)从源地址复制到目标地址。函数原型为 char* strcpy(char* destination, const char* source)。需要注意的是,该函数会复制整个字符串,包括 NULL 终止…...

用CPU大法忽悠ChatGPT写前端,油猴子工具库+1
文章目录用CPU大法忽悠ChatGPT写前端,油猴子工具库1源起对话1. 作为一名天才js程序员,开发一个油猴子脚本,实现所有浏览器网页的自动下滑功能,每一个步骤都加上中文注释2. 加一个按钮,只有我点击了按钮才会开始自动下滑…...
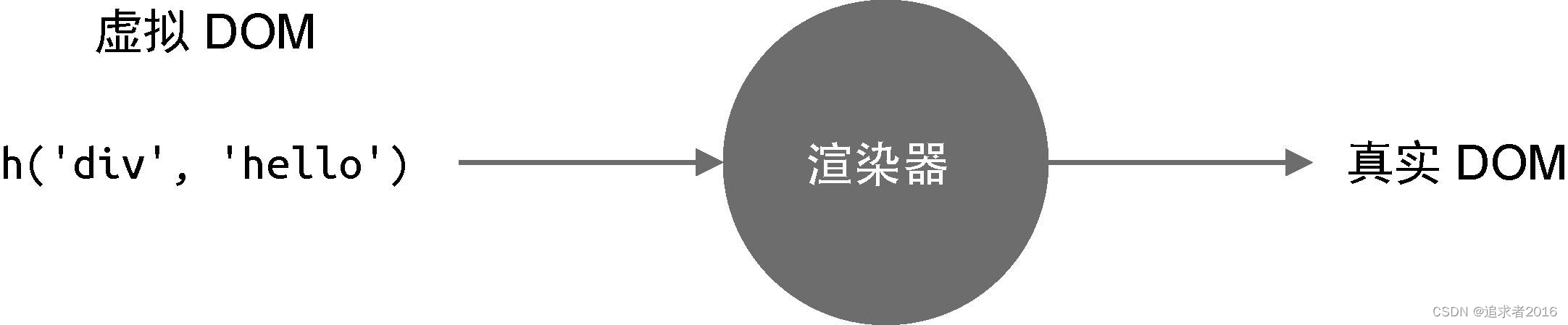
初识虚拟DOM渲染器
初识虚拟DOM渲染器什么是虚拟DOM什么是渲染器渲染器的实现组件是什么什么是虚拟DOM 首先简单说一下什么是虚拟DOM,虚拟DOM就是一个描述真实DOM的JS对象 例如: 真实的DOM元素 <div onClick"alert(click me)">click me</div>可以…...
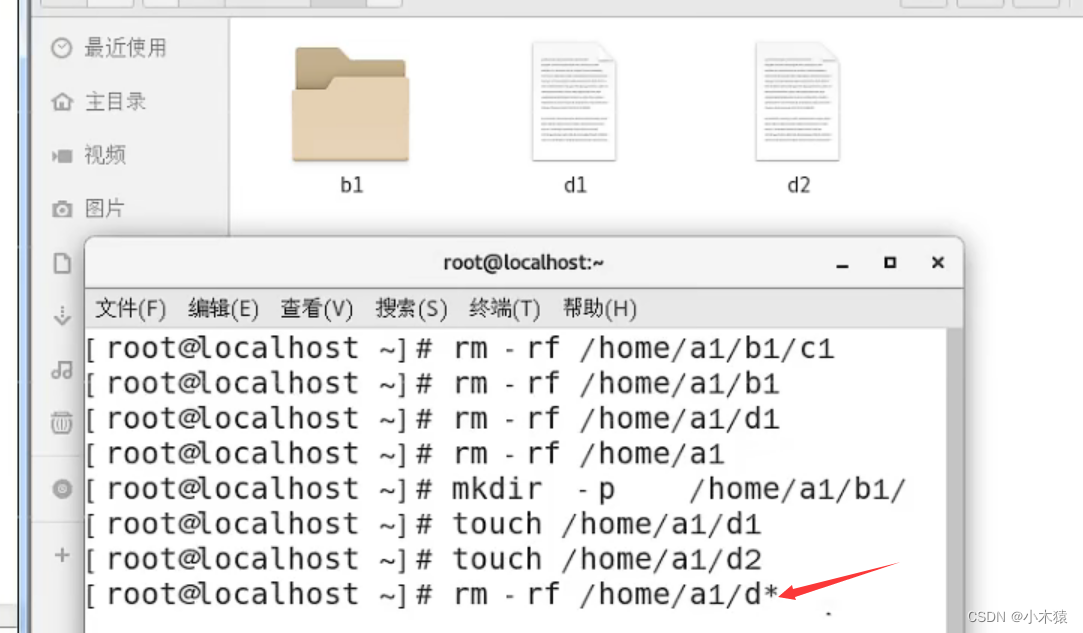
工作日志day03
同时构建静态和动态库 //如果用这种方式,只会构建一个动态库,虽然静态库的后缀是.a ADD_LIBRARY(hello SHARED ${LIBHELLO_SRC}) ADD_LIBRARY(hello STATIC ${LIBHELLO_SRC}) //修改静态库的名字,这样是可以的,但是我们往往希望他…...

【数据挖掘与商务智能分析】第三章 线性回归模型
一元线性回归 一元线性回归的代码实现 1. 绘制散点图 import matplotlib.pyplot as plt X = [[1], [2], [4], [5]] Y...
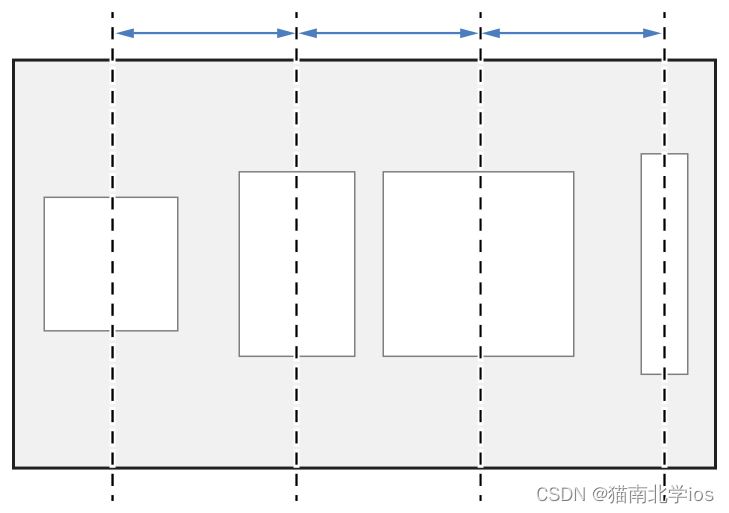
iOS开发之UIStackView基本运用
UIStackView UIStackView是基于自动布局AutoLayout,创建可以动态适应设备方向、屏幕尺寸和可用空间的任何变化的用户界面。UIStackView管理其ArrangedSubview属性中所有视图的布局。这些视图根据它们在数组中的顺序沿堆栈视图的轴排列。由axis, distribution, align…...

【java】为什么 main 方法是 public static void ?
main 方法是我们学习Java编程语言时知道的第一个方法,你是否曾经想过为什么 main 方法是 public、static、void 的。当然,很多人首先学的是C和C,但是在Java中main方法与前者有些细微的不同,它不会返回任何值,为什么 ma…...
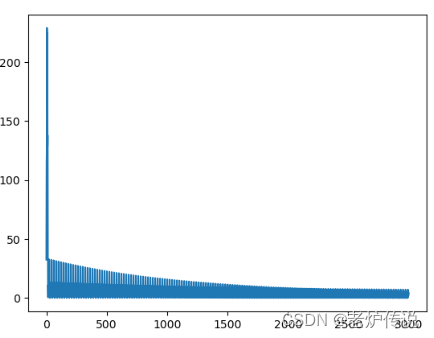
最简单的线性回归模型-标量
首先考虑yyy为标量,www为标量的情况,那么我们的线性函数为ywxbywxbywxb。每批输入的量batch size 为111,每批输入的xxx为一个标量,设为x∗x^*x∗,标签yyy同样为一个标量,设为y∗y^*y∗。因此每批训练的损失…...

k8s-Kubernetes集群升级
文章目录前言一、集群升级1.部署cri-docker (所有集群节点)2.升级master节点3.升级worker节点前言 一、集群升级 https://v1-24.docs.kubernetes.io/zh-cn/docs/tasks/administer-cluster/kubeadm/kubeadm-upgrade/ 1.部署cri-docker (所有…...
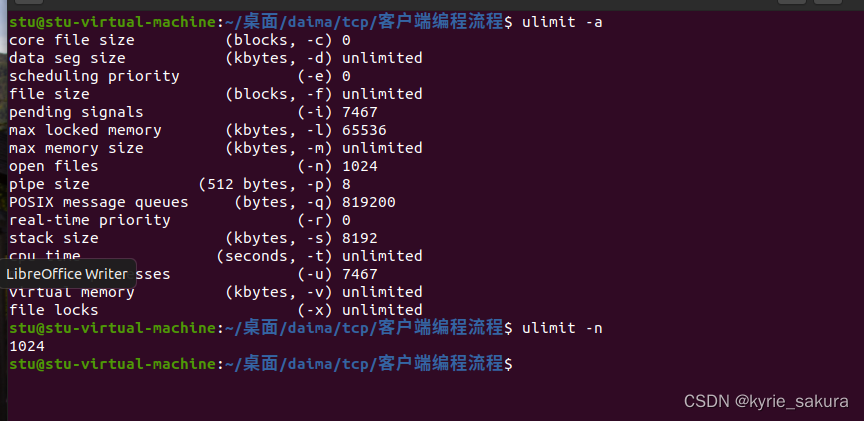
Linux25 -- 监听队列链接上限测试、命令uname、ulimit
一、监听队列链接上限测试 1、res listen(sockfd,5); //创建监听队列res listen(sockfd,5);不懂版本有不同的限制,2.6早期版本有限制为128,超过默认为128,可使用uname -a 查看版本 2、测试将链接数到达上限, 方法࿱…...

idea:地址被占用
问题启动idea报:java.net.BindException: Address already in use: bind,具体截图如下:解决步骤1、首先想到的是改idea端口,但按网上方法试下了几个4位数和5位数的端口,没啥作用2、根据idea抛异常的弹出框提示…...
)
JavaScript常用小技巧(js优化)
JavaScript常用小技巧(js优化)常见JS操作1、解构交换两数2、短路赋值3、if 判断优化4、 switch 判断优化6、动态正则匹配Number1、幂运算2、安全计算String1、反转字符串、判断是否回文数2、数组求和3、初始化二维数组Object1、对象遍历2、冻结对象3、解…...

【项目实战】MySQL 5.7中的关键字与保留字详解
一、什么是关键字和保留字 关键字是指在SQL中有意义的字。 某些关键字(例如SELECT,DELETE或BIGINT)是保留的,需要特殊处理才能用作表和列名称等标识符。 这一点对于内置函数的名称也适用。 二、如何使用关键字和保留字 非保留关…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

Caliper 配置文件解析:config.yaml 和 fisco-bcos.json 附加在caliper中执行不同的合约方法
Caliper 配置文件解析:config.yaml 和 fisco-bcos.json Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO…...

全面解析网络端口:概念、分类与安全应用
在计算机网络的世界里,数据的传输与交互如同一场繁忙的物流运输,而网络端口就是其中不可或缺的 “货运码头”。无论是日常浏览网页、收发邮件,还是运行各类网络服务,都离不开网络端口的参与。本文将深入介绍网络端口的相关知识&am…...

leetcode238-除自身以外数组的乘积
leetcode 238 思路 可以在不使用除法的情况下,利用前缀积和后缀积来实现解答 前缀积:对每个位置,计算当前数字左侧的所有数字的乘积后缀积:对每个位置,计算当前数字右侧的所有数字的乘积 结合这两种思想࿰…...

AI短视频创富营
课程内容: 相关资料 【第一章】前期准备 001.【涨粉技巧】新账号如何快速涨粉?_ev(1).mp4 002.【带贷权限】如何开通账号带贷权限?(1).mp4 003.【费用缴纳】如何缴纳账号保证金?_ev(1).mp4 004.【账号检测】如何检测账号是否限流?(1).mp4 005.【风险规避…...

MySQL 索引优化(Explain执行计划) 详细讲解
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 MySQL 索引优化(Explain执行计划…...
