20240319-2-机器学习基础面试题
-
⽼板给了你⼀个关于癌症检测的数据集,你构建了⼆分类器然后计算了准确率为 98%, 你是否对这个模型很满意?为什么?如果还不算理想,接下来该怎么做?
首先模型主要是找出患有癌症的患者,模型关注的实际是坏样本。其次一般来说癌症的数据集中坏样本比较少,正负样本不平衡。
准确率指的是分类正确的样本占总样本个数的比率
Accuracy = n correct n total \text { Accuracy }=\frac{n_{\text {correct }}}{n_{\text {total }}} Accuracy =ntotal ncorrect
其中 n c o r r e c t n_{correct} ncorrect为正确分类样本的个数, n t o t a l n_{total} ntotal为总样本分类的个数。当好样本(未患病)的样本数占99%时,模型把所有的样本全部预测为好样本也可以获得99%的准确率,所以当正负样本非常不平衡时,准确率往往会偏向占比大的类别,因此这个模型使用准确率作为模型的评估方式并不合适。
鉴于模型关注的实际是坏样本,建议使用召回率(Recall )作为模型的评估函数。
Recall 是分类器所预测正确的正样本占所有正样本的比例,取值范围为[0,1],取值越大,模型预测能力越好。
R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP其次,使用类别不平衡的解决方案:
常见的处理数据不平衡的方法有:重采样、Tomek links、SMOTE、NearMiss等
除此之外:还可以使用模型处理:使用多种树模型算法,使用多种重采样的训练集,对少数样本预测错误增大惩罚,避免使用Accuracy,可以用confusion matrix,precision,recall,f1-score,AUC,ROC等指标。
-
怎么判断⼀个训练好的模型是否过拟合? 如果判断成了过拟合,那通过什么办法 可以解决过拟合问题?
模型在验证集合上和训练集合上表现都很好,而在测试集合上变现很差。
解决过拟合的办法:
-
特征降维
-
添加正则化,降低模型的复杂度
-
Dropout
-
Early stopping
-
交叉验证
-
决策树剪枝
-
选择合适的网络结构
-
-
对于线性回归,我们可以使⽤ Closed-Form Solution, 因为可以直接把导数设置 为 0,并求出参数。在这个 Closed-Form ⾥涉及到了求逆矩阵的过程,什么时候不能求出其逆矩阵?这时候如何处理?
-
什么是闭式解(Closed-Form Solution)
解析解(Analytical solution) 就是根据严格的公式推导,给出任意的自变量就可以求出其因变量,也就是问题的解,然后可以利用这些公式计算相应的问题。所谓的解析解是一种包含分式、三角函数、指数、对数甚至无限级数等基本函数的解的形式。用来求得解析解的方法称为解析法(Analytical techniques),解析法即是常见的微积分技巧,例如分离变量法等。解析解是一个封闭形式(Closed-form) 的函数,因此对任一自变量,我们皆可将其带入解析函数求得正确的因变量。因此,解析解也被称为封闭解(Closed-form solution)。
数值解(Numerical solution) 是采用某种计算方法,如有限元法, 数值逼近法,插值法等得到的解。别人只能利用数值计算的结果,而不能随意给出自变量并求出计算值。当无法藉由微积分技巧求得解析解时,这时便只能利用数值分析的方式来求得其数值解了。在数值分析的过程中,首先会将原方程加以简化,以利于后来的数值分析。例如,会先将微分符号改为差分(微分的离散形式)符号等,然后再用传统的代数方法将原方程改写成另一种方便求解的形式。这时的求解步骤就是将一自变量带入,求得因变量的近似解,因此利用此方法所求得的因变量为一个个离散的数值,不像解析解为一连续的分布,而且因为经过上述简化的操作,其正确性也不如解析法可靠。
简而言之,解析解就是给出解的具体函数形式,从解的表达式中就可以算出任何对应值;数值解就是用数值方法求出近似解,给出一系列对应的自变量和解。
参考:https://blog.csdn.net/weicao1990/article/details/90742414
-
什么时候不能求出其逆矩阵
满秩矩阵或者方阵才有逆矩阵,当一个矩阵不满秩,在对角线上存在为0的特征值,求逆的时候 1 0 \frac{1}{0} 01无法计算从而不可逆,那我们给它加上一个单位矩阵,这样它就不为0了,
求解的时候加上单位矩阵其实就是对线性回归引入正则化的过程
-
-
关于正则,我们⼀般采⽤ L2 或者 L1, 这两个正则之间有什么区别? 什么时候需要⽤ L2, 什么时候需要⽤ L1?
L1正则化(也叫Lasso回归)是在目标函数中加上与系数的绝对值相关的项,而L2正则化(也叫岭回归)则是在目标函数中加上与系数的平方相关的项。
Lasso 和岭回归系数估计是由椭圆和约束函数域的第一个交点给出的。因为岭回归的约束函数域没有尖角,所以这个交点一般不会产生在一个坐标轴上,也就是说岭回归的系数估计全都是非零的。然而,Lasso 约束函数域在每个轴上都有尖角,因此椭圆经常和约束函数域相交。发生这种情况时,其中一个系数就会等于 0。
L2正则化会使参数的绝对值变小,增强模型的稳定性(不会因为数据变化而产生很大的震荡);而L1正则化会使一些参数为零,可以实现特征稀疏, 增强模型解释性。
-
正则项是否是凸函数?请给出证明过程。
相关概念:凸集,凸函数
因此证明正则项是否是凸函数,需要证明:
-
f ( x ) f(\boldsymbol{x}) f(x) 在 D D D 上二阶连续可微
-
$f(\boldsymbol{x}) $的Hessian(海塞)矩阵在 D D D上是半正定
-
半正定矩阵的判定定理之一:若实对称矩阵的所有顺序主子式均为非负,则该矩阵为半 正定矩阵。
参考:https://www.bilibili.com/video/BV1Mh411e7VU?p=2
-
-
什么叫 ElasticNet? 它主要⽤来解决什么问题? 具体如何去优化?
弹性回归是岭回归和lasso回归的混合技术,它同时使用 L2 和 L1 正则化。当有多个相关的特征时,弹性网络是有用的。lasso回归很可能随机选择其中一个,而弹性回归很可能都会选择。
β ^ = argmin β ( ∥ y − X β ∥ 2 + λ 2 ∥ β ∥ 2 + λ 1 ∥ β ∥ 1 ) \hat{\beta}=\underset{\beta}{\operatorname{argmin}}\left(\|y-X \beta\|^{2}+\lambda_{2}\|\beta\|^{2}+\lambda_{1}\|\beta\|_{1}\right) β^=βargmin(∥y−Xβ∥2+λ2∥β∥2+λ1∥β∥1)- 在高度相关变量的情况下,它支持群体效应。
- 它对所选变量的数目没有限制
- 它具有两个收缩因子 λ1 和 λ2。
参考:https://www.zhihu.com/search?type=content&q=ElasticNet
-
基于 Coordinate Descent 算法给出 LASSO 的优化推导过程。
参考:https://www.cnblogs.com/zzqingwenn/p/10874522.html
-
请推导逻辑回归模型: ⽬标函数的构建,最优解的求解过程(SGD)需要详细写出。
-
在数据线性可分的情况下,为什么逻辑回归模型的参数会变得⽆穷⼤?怎么避免?
-
逻辑回归是线性还是⾮线性模型? 为什么? 请给出推导过程。
logistic回归属于线性模型还是非线性模型?
-
我们在使⽤逻辑回归模型的时候,通常把连续性变量切分成离散型变量,为什么? 有什么好处?
-
朴素⻉贝叶斯应为叫 Naïve Bayes, 请说出朴素⻉贝叶斯模型的构建过程以及预测过程, 并说出为什么叫“naive”?
-
什么叫⽣成模型,什么叫判别模型? 朴素⻉贝叶斯,逻辑回归,HMM,语⾔模型 中哪⼀个是⽣成模型,哪⼀个是判别模型?
生成式模型先对数据的联合分布 进行建模,然后再通过贝叶斯公式计算样本属于各类别的后验概率 。
判别式模型直接进行条件概率建模,由数据直接学习决策函数 或条件概率分布 作为预测的模型。判别方法不关心背后的数据分布,关心的是对于给定的输入,应该预测什么样的输出。
-
特点
生成式模型的特点在于,其可以从统计的角度表示数据的分布情况,能反映同类数据本身的相似度,不关心各类的边界在哪;
而判别式模型直接学习的是条件概率分布,所以其不能反映训练数据本身的特性,其目的在于寻找不同类别之间的最优分界面,反映异类数据之间的差异。
由生成模型可以得到判别模型,但由判别模型得不到生成模型。
当存在隐变量(当我们找不到引起某一现象的原因的时候,我们就把这个在起作用但是无法确定的因素,叫“隐变量”) 时,仍可以利用生成方法学习,此时判别方法不能用。因为生成式模型同时对 x 和 y 建立概率模型,所以如果 x 中有出现没有观察到的量或者只有部分 y 的时候,就可以很自然地使用 EM 算法 来进行处理。极端情况下,在完全没有 y 信息的情况下,GM 仍然是可以工作的——无监督学习可以看成是 GM 的一种。
优点 缺点 代表算法 生成式模型 1. 由于统计了数据的分布情况,所以其实际带的信息要比判别模型丰富,对于研究单类问题来说也比判别模型灵活性强;
2. 模型可以通过增量学习得到(增量学习是指一个学习系统能不断地从新样本中学习新的知识,并能保存大部分以前已经学习到的知识。);
3. 收敛速度更快,当样本容量增加的时,生成模型可以更快的收敛于真实模型;
4. 隐变量存在时,也可以使用。1. 学习和计算过程比较复杂,由于学习了更多的样本信息,所以计算量大,如果我们只是做分类,就浪费了这部分的计算量;
2. 准确率较差;
3. 往往需要对特征进行假设,比如朴素贝叶斯中需要假设特征间独立同分布,所以如果所选特征不满足这个条件,将极大影响生成式模型的性能。朴素贝叶斯、贝叶斯网络、隐马尔可夫模型、隐马尔可夫模型 判别式模型 1. 由于关注的是数据的边界,所以能清晰的分辨出多类或某一类与其他类之间的差异,所以准确率相对较高;
2. 计算量较小,需要的样本数量也较小;1. 不能反映训练数据本身的特性;
2. 收敛速度较慢k 近邻法、决策树、逻辑斯谛回归模型、最大熵模型、支持向量机、条件随机场 参考 :https://cloud.tencent.com/developer/article/1544597
-
-
决策树与随机森林的区别是什么? 如果让你选择,你会使⽤哪个模型,为什么?
-
请介绍 k-means 算法的流程, 写出 k-means 模型的⽬标函数。K-means 求解 过程跟 EM 算法之间有什么关系? K-MEANS ⽬标函数是否是 convex?
-
什么叫 EM 算法?有哪些经典模型的求解过程会⽤到 EM 算法?
-
EM 算法是否⼀定会收敛?EM 算法给出的全局最优还是局部最优?
-
请解释什么叫 MLE,什么叫 MAP? 请说明它们之间的区别。 在数据量⽆穷多的 时候,是否 MAP 趋近于 MLE 估计?
-
请解释什么叫召回率,精确率,F1 Measure,ROC, AUC? 什么时候需要⽤到这 些?
-
数据集拥有⾮常多的特征,但样本个数有限,所以计划做特征选择,有哪些⽅法 可以⽤来做特征选择呢?
-
随机森林和 Gradient Boosting Tree 之间的区别是什么?
-
在构建决策树模型的时候,我们⼀般不会构建到底,也就做⼀些剪枝的操作,为 什么? 然⽽,在构建随机森林的时候剪枝的操作不像决策树⾥那么重要,为什么?
-
什么样的数据是不均衡数据(imbalance data)? 需要怎么样的处理?
-
什么是 kernel trick? 它有什么好处?并写出 RBF kernel, Gaussian Kernel 的公 式。
-
什么 Mercer’s Theorem, 阐述⼀下具体的细节。
-
使⽤⾮线性 Kernel 有哪些优缺点?重点介绍⼀下效率上的缺点,并说明为什么会 产⽣效率上的缺点?
-
SVM 是 margin-based classifier, 试着推导 SVM,并说明什么是 KKT 条件。
-
如果不考虑 kernel, 逻辑回归和 SVM 的区别是什么?
-
在随机梯度下降法⾥怎么有效地选择学习率?有哪些常⻅见的动态改变学习率的策略?
-
深度学习是什么? 它跟所谓的传统的学习模型有什么本质的区别?从模型的 Capacity, Hierarchical Representation 的⻆角度举例说明。
-
PCA 的原理是什么? 推导⼀下 PCA 的过程。
-
什么叫 PAC 理论? 它主要⽤来解决什么问题?
-
解释⼀下矩阵分解算法以及怎么⽤到推荐系统⾥,并利⽤梯度下降法来推导矩阵 分解过程。
-
模型参数和超参数的区别是什么?
-
什么叫因变量,以及因变量模型?
-
超参数的选择⽅法有哪些?⾄少列出 4 种以上来说明,并说出其优缺点。
-
什么是 XGBoost 模型?说明⼀下其技术细节。
-
怎么把 K-means 算法应⽤到⼤规模的数据上? 有什么 Scalable 的⽅法?(hint:mini-batch, triangle inequality)
-
K-means 算法与 GMM 之间有什么关系?
-
在深度学习模型⾥,有哪些技术可以⽤来避免过拟合现象?
-
CNN ⾥⾯ POOLING 的作⽤是什么? 卷积的作⽤是什么?
-
在分类问题⾥,最后⼀层通常使⽤ softmax,请写 softmax 函数。
-
描述⼀下 SGD, Adagrad, Adam 算法之间的区别,什么时候使⽤ SGD? Adagrad? Adam 算法?
-
简 单 描 述 ⼀ 下 什 么 是 Variational Autoencoder(VAE), 什 么 是 Generative Adversial Network(GAN)
-
Dropout 和 Bagging 模型的关系是什么? 为什么 Dropout 可以起到避免过拟合 的作⽤?
-
对于拥有两层隐含层的神经⽹络(MLP), 请⼿动推导其 BP 算法的细节。
-
使⽤ KNN 会遇到⼀些效率上的问题,请说明如何使⽤ LSH(latent semantic hashing)来做近似操作?
-
在朴素⻉贝叶斯和语⾔模型中我们通常会使⽤ smoothing 技术,请简述⼏个常⻅见 的 smoothing ⽅法以及它们优缺点。
相关文章:

20240319-2-机器学习基础面试题
⽼板给了你⼀个关于癌症检测的数据集,你构建了⼆分类器然后计算了准确率为 98%, 你是否对这个模型很满意?为什么?如果还不算理想,接下来该怎么做? 首先模型主要是找出患有癌症的患者,模型关注的…...

0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…...

python中的__dict__
类的__dict__返回的是:类的静态函数、类函数、普通函数、全局变量以及一些内置的属性都是放在类的__dict__里的, 而实例化对象的:__dict__中存储了一些类中__init__的一些属性值。 import的py文件 __dict__返回的是:__init__的…...

数学分析复习:无穷乘积
文章目录 无穷乘积定义:无穷乘积的收敛性命题:无穷乘积的Cauchy收敛准则正项级数和无穷乘积的联系 本篇文章适合个人复习翻阅,不建议新手入门使用 无穷乘积 设复数列 { a n } n ≥ 1 \{a_n\}_{n\geq 1} {an}n≥1,设对任意 …...

02 React 组件使用
import React, { useState } from react;// 定义一个简单的函数式组件 function Counter() {// 使用 useState hook 来创建一个状态变量 count,并提供修改该状态的函数 setCountconst [count, setCount] useState(0);// 在点击按钮时增加计数器的值const increment…...
你就是上帝
你就是上帝:Jv程序员,请你站在上帝或神的角度 1.万物皆有裂缝 按照西方文化(宗教神话,古希腊、古罗马等),上帝创建了人; 创建人之前,还创建了人的居所或地盘/栖息地(伊…...

Spring Cloud: openFegin使用
文章目录 一、OpenFeign简介二、Springboot集成OpenFeign1、引入依赖2、EnableFeignClients注解(1)应用(2)属性解析 3、 FeignClient(1)应用(2)属性解析(3)向…...

流畅的 Python 第二版(GPT 重译)(二)
第三章:字典和集合 Python 基本上是用大量语法糖包装的字典。 Lalo Martins,早期数字游牧民和 Pythonista 我们在所有的 Python 程序中都使用字典。即使不是直接在我们的代码中,也是间接的,因为dict类型是 Python 实现的基本部分。…...

Flutter 旋转动画 线性变化的旋转动画
直接上代码 图片自己添加一张就好了 import dart:math;import package:flutter/material.dart;import package:flutter/animation.dart;void main() > runApp(MyApp()); //旋转动画 class MyApp extends StatelessWidget {overrideWidget build(BuildContext context) {re…...

【Web应用技术基础】HTML(5)——案例1:展示简历信息
样式: 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>展示简历信息…...
)
ethers.js:wallet(创建钱包,导入助记词,导入私钥)
Wallet Wallet类继承了Signer,可以使用私钥作为外部拥有帐户(EOA)的标准对交易和消息进行签名。 npm install ethers@5.4.0// 引入 import {ethers } from ethers创建新钱包 this.provider = new ethers.providers.Web3Provider(window...

面试笔记——Java集合篇
Java集合框架体系 重点:单列集合——ArrayList、LinkedList;双列集合——HashMap、ConcurrentHashMap。 List相关 数组(Array) 是一种用连续的内存空间存储相同数据类型数据的线性数据结构。 数组获取其他元素: 为什…...

在 IntelliJ IDEA 中使用 Terminal 执行 git log 命令后的退出方法
前言 IntelliJ IDEA 是一款广受欢迎的集成开发环境,它内置了强大的终端工具,使得开发者无需离开IDE就能便捷地执行各种命令行操作,包括使用 Git 进行版本控制。在 IDEA 的 Terminal 中执行 git log 命令时,由于该命令会显示项目的…...
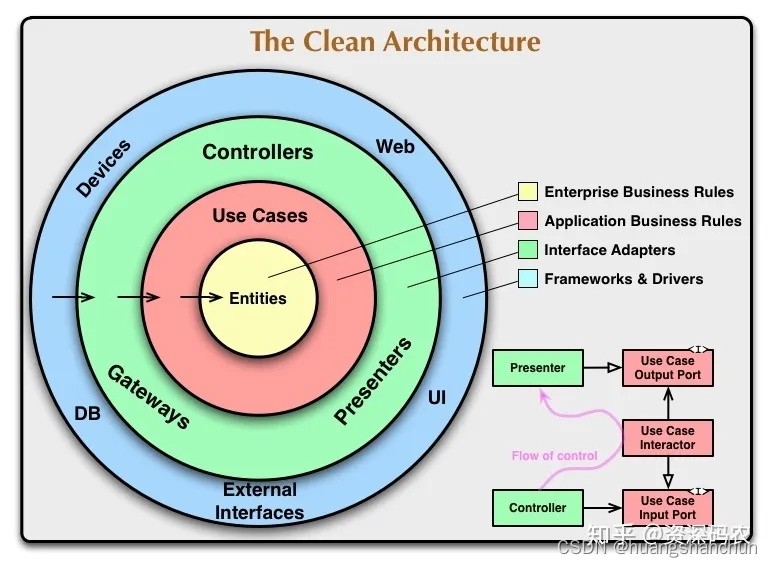
架构整洁之道-读书总结
1 概述 1.1 关于本书 《架构整洁之道》(Clean Architecture: A Craftsman’s Guide to Software Structure and Design)是由著名的软件工程师Robert C. Martin(又称为Uncle Bob)所著。这本书提供了软件开发和架构设计的指导原则…...

蓝桥杯学习笔记(贪心)
在很久很久以前,有几个部落居住在平原上,依次编号为1到n。第之个部落的人数为 t 有一年发生了灾荒,年轻的政治家小蓝想要说服所有部落一同应对灾荒,他能通过谈判来说服部落进行联台。 每次谈判,小蓝只能邀请两个部落参…...

【无标题】如何使用 MuLogin 设置代理
如何使用 MuLogin 设置代理 使用 MuLogin 浏览器设置我们的代理,轻松管理多个社交媒体或电子商务帐户。 什么是MuLogin? MuLogin 是一款虚拟反检测浏览器,使用户能够管理多个电子商务、社交媒体和广告帐户,而无需验证码或 IP 禁…...

芒果YOLOv8改进135:主干篇GCNet,统一为全局上下文建模global context结构,即插即用,助力小目标检测,轻量化的同时精度性能涨点
该专栏完整目录链接: 芒果YOLOv8深度改进教程 芒果专栏 基于 GCNet 的改进结构,改进源码教程 | 详情如下🥇 💡本博客 改进源代码改进 适用于 YOLOv8 按步骤操作运行改进后的代码即可 即插即用 结构。博客 包括改进所需的 核心结构代码 文件 论文:https://arxiv.org/a…...
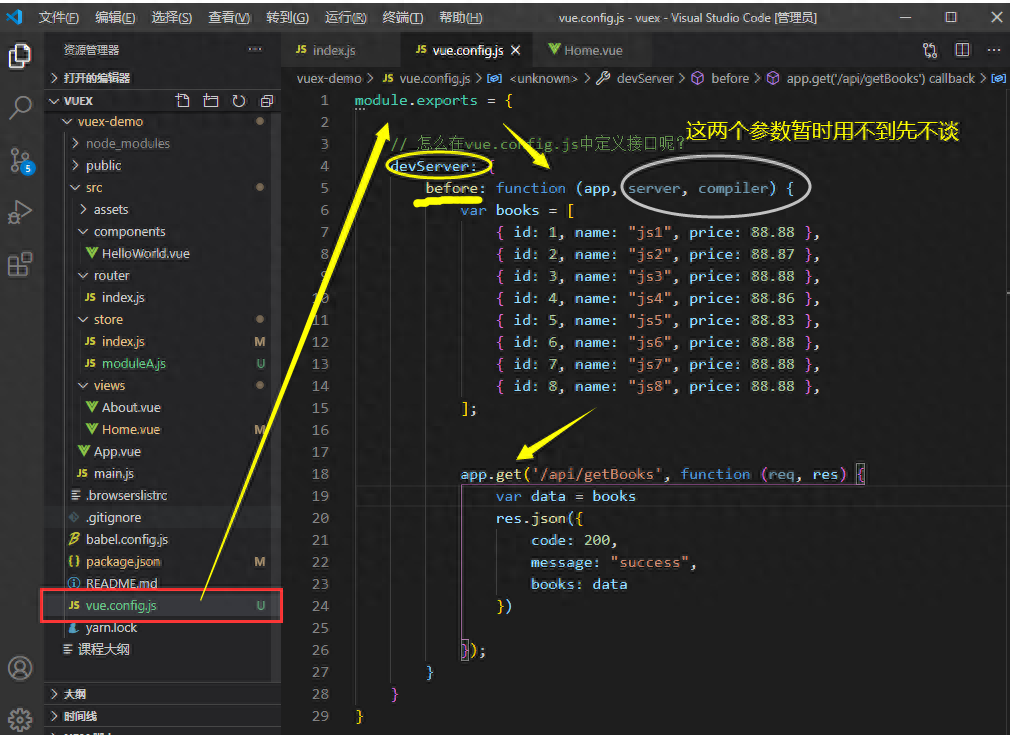
全面:vue.config.js 的完整配置
vue.config.js是Vue项目的配置文件,用于配置项目的构建、打包和开发环境等。 在Vue CLI 3.0之后,项目的配置文件从原来的build和config目录下的多个配置文件,合并成了一个vue.config.js文件。这个文件可以放在项目的根目录下,用于…...

海量数据处理项目-账号微服务注册Nacos+配置文件增加
海量数据处理项目-账号微服务注册Nacos配置文件增加 导入生成好的代码 model (为啥不放common项目,如果是确定每个服务都用到的依赖或者类才放到common项目) mapper 类接口拷贝 resource/mapper文件夹 xml脚本拷贝 controller service 不拷贝 Mybatis plus配置控制…...

DNS 服务 Unbound 部署最佳实践
文章目录 安装unbound-control配置启动服务测试 参考: 官网地址:https://nlnetlabs.nl/projects/unbound/about/ 详细文档:https://unbound.docs.nlnetlabs.nl/en/latest/index.html DNS服务Unbound部署于使用 https://cloud.tencent.com/…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
