基于Givens旋转完成QR分解进而求解实矩阵的逆矩阵
基于Givens旋转完成QR分解进而求解实矩阵的逆矩阵
目录
前言
一、Givens旋转简介
二、Givens旋转解释
三、Givens旋转进行QR分解
四、Givens旋转进行QR分解数值计算例子
五、求逆矩阵
六、MATLAB仿真
七、参考资料
总结
前言
在进行QR分解时,HouseHolder变换一次将一个向量除第一个元素以外都转化成零。而有一种方法,可以每次将向量的一个元素转化成0,也可以最终达到正交化的目的,它就是Givens旋转。Givens旋转矩阵是正交矩阵,使用Givens旋转很容易就可以将一个向量的某个分量的某个指定分量化为0。本文会通过列举例子说明如何将一个矩阵通过Givens旋转分解为Q矩阵和R矩阵,最后,会用MATLAB进行仿真,当然,代码也会分享出来。
提示:以下是本篇文章正文内容,希望能帮助到各位,转载请附上链接。
一、Givens旋转简介
Givens旋转矩阵是正交矩阵,使用Givens旋转很容易就可以将一个向量的某个分量的某个指定分量化为0。
本文中主要考虑实数的情况。
2×2的Givens旋转矩阵如下:
其中
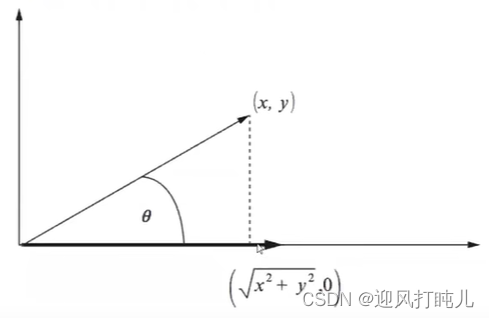
那么就可以将向量旋转到x轴上面去,如下图所示。当然改变正余弦函数也能旋转到y轴上面去。
即
可以把简写三角函数,如下所示
二、Givens旋转解释
我们将向量看成一个复数,即
则
将其也看成一个复数
对比和
,学过复数的话,显然就能看出这是顺时针旋转了
的角度。
三、Givens旋转进行QR分解
下面我们来说明如何通过Givens旋转来实现QR分解。其实原理很简单,就是通过将原矩阵A的主对角线下方的元素都通过Givens旋转置换成0,形成上三角矩阵R,同时左乘的一系列Givens矩阵相乘得到一个正交阵Q。
如下图所示,G(m,n)是Givens旋转矩阵,相当于用某一列的第m个元素去将第n个元素清零。

也可以通过下图来理解,其中×表示没有发生变化的元素,m表示值改变的元素,每一个向右的箭头表示原矩阵左乘了1次Givens矩阵。

由上图我们会发现清一个0时只影响两行,所以对一个高阶矩阵,在清某一列的几个0时可以同时执行,加快计算速度。比如对于4×4阶矩阵,可以在选第1列的第1个元素去将第一列的第2个元素清零的同时,也选择第1列的第3个元素去将第一列的第4个元素清零。
四、Givens旋转进行QR分解数值计算例子
设矩阵,用Givens旋转的方法对其进行QR分解。
解:由于其第1列的第2个元素已经为0了,不用对它进行消0操作,我们首先用第1列的第1个元素对第1列的第3个元素清0。
易求
则Givens矩阵可写为
所以
接下来对上面结果右下角的四个元素进行Givens旋转,用3去将-4消为0。
易求
则Givens矩阵可写为
所以
所以
所以
故
五、求逆矩阵
分解得到Q矩阵和R矩阵后可参考下面两篇文章进行求逆矩阵:
施密特正交化QR分解求逆矩阵与MATLAB仿真:http://t.csdnimg.cn/d1IGR
一种基于约化因子上三角矩阵求逆方法与MATLAB仿真:http://t.csdnimg.cn/uZJkG
六、MATLAB仿真
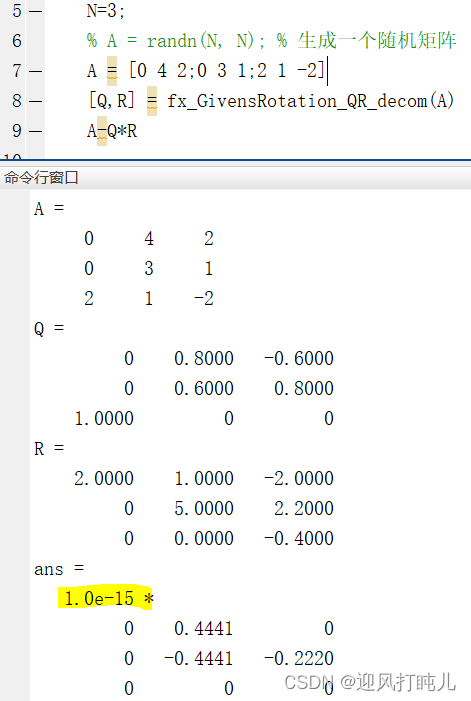
可见,仿真结果和上面的数值计算结果吻合。
七、参考资料
参考资料:https://download.csdn.net/download/m0_66360845/89043215
总结
以上就是今天要讲的内容,本文介绍了Givens旋转,在我理解的基础上讲解了它的几何意义,以及怎样用它将可逆矩阵分解成Q矩阵和R矩阵。同时,也用MATLAB验证了Givens旋转 QR分解算法。
相关文章:

基于Givens旋转完成QR分解进而求解实矩阵的逆矩阵
基于Givens旋转完成QR分解进而求解实矩阵的逆矩阵 目录 前言 一、Givens旋转简介 二、Givens旋转解释 三、Givens旋转进行QR分解 四、Givens旋转进行QR分解数值计算例子 五、求逆矩阵 六、MATLAB仿真 七、参考资料 总结 前言 在进行QR分解时,HouseHolder变换…...
学习使用xbox手柄控制小乌龟节点移动
使用xbox手柄控制小乌龟,首先要下载joy功能包,发布sensor_msgs话题也就是手柄和ros通信的话题。 下载的步骤就根据官方文档即可 joy/Tutorials/ConfiguringALinuxJoystick - ROS Wiki 这里我提供一下具体步骤 第一步 安装joy 首先安装对应系统版本的…...

OpenLayers6实战,OpenLayers绘制特殊图形,OpenLayers绘制四角形(菱形),OpenLayers绘制菱形
专栏目录: OpenLayers实战进阶专栏目录 前言 本章讲解如何使用OpenLayers6实现绘制特殊图形,以绘制四角形(菱形),OpenLayers绘制菱形的功能为例。 本章核心代码不依赖任何第三方插件,只依赖OpenLayers。 需要注意的是两个操作按钮需要引入ElementUI 二、依赖和使用 &q…...

虚拟机如何在原有磁盘上扩容
虚拟机未开启状态–菜单栏–虚拟机–快照–拍摄快照–拍摄快照– 菜单栏–虚拟机–快照–快照管理器–点击刚刚的快照1–删除–是– 文件–新建或者打开–硬盘(以本人Win 10.64.3GL为例)–虚拟机设置–硬件– 硬盘(SATA)–磁盘实…...
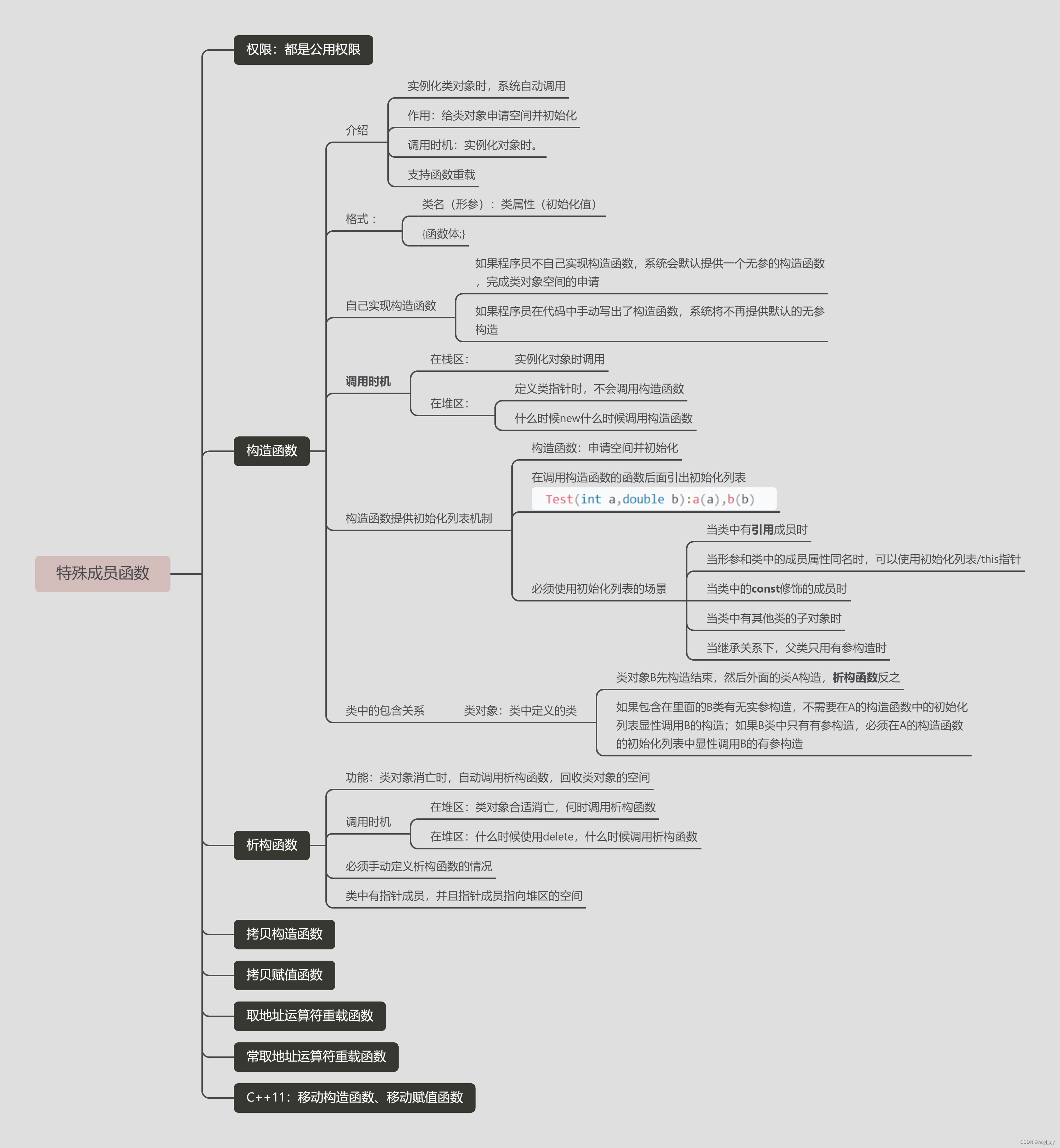
2024-03-27 作业
作业要求: 整理课上代码整理思维导图完成下面类 作业1: 完成了 作业2: 作业3: class myString {private:char *str; //记录c风格的字符串int size; //记录字符串的实际长度public://无参构造myString():si…...
C语言二叉树和堆(个人笔记)
二叉树和堆 二叉树1二叉树的概念和结构1.1特殊的二叉树1.2二叉树的性质(规定根节点的层数为1)1.3二叉树的存储结构 2.二叉树的顺序结构和实现2.1二叉树的顺序结构2.2堆的概念和结构2.3堆的实现2.4堆的应用2.4.1堆排序 2.5TOP-K问题 3.二叉树的遍历4.二叉…...
重学SpringBoot3-Profiles介绍
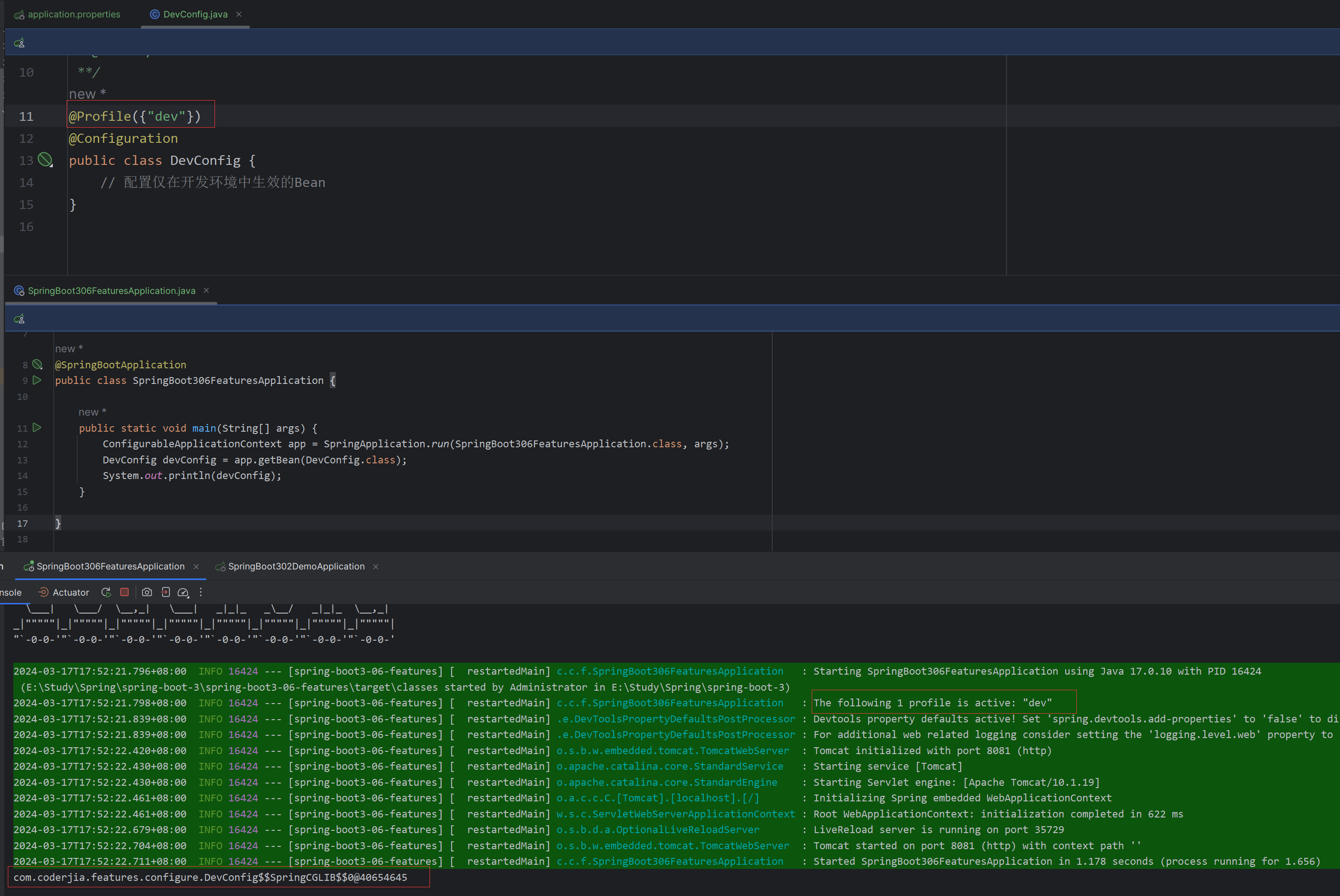
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-Profiles介绍 Profiles简介如何在Spring Boot中使用Profiles定义Profiles激活ProfilesIDEA设置active profile使用Profile-specific配置文件 条件化Bean…...

Transformer 论文阅读笔记
文章目录 前言论文阅读研究现状工作内容模型架构训练过程实验结果模型代码 其他评价 前言 Transformer可以说是深度学习领域最重要的,里程碑式的工作之一,发表于2017年的NIPS。该模型开创了自MLP(多层感知机)、CNN(卷…...

Vue 3中ref和reactive的区别
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
oracle19c adg搭建
一、环境搭建 主机IPora19192.168.232.111ora19std192.168.232.112 本文结合:https://blog.csdn.net/weixin_63131036/article/details/136635553 1.配置网络yum源 1.删除redhat7.0系统自带的yum软件包; rpm -qa|grep yum >oldyum.pkg 备份原信息 …...
关闭Elasticsearch built-in security features are not enabled
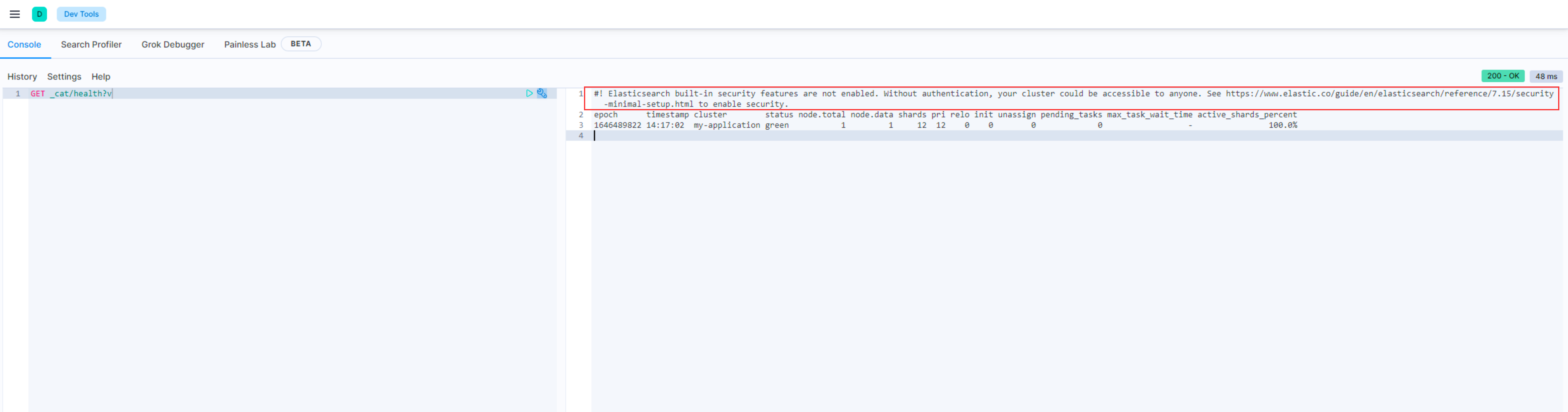
禁用Kibana安全提示(Elasticsearch built-in security features are not enabled) Kibana提示#! Elasticsearch built-in security features are not enabled. Without authentication, your cluster could be accessible to anyone. See https://www.e…...

MC0248 密码判断器(判断强弱密码)
原题链接<---- islower 小写字母判断 isupper 大写字母判断 isdigit 数字判断 题目: 小码哥在是一位密码领域的初学者,有一天他的老师给他了一串密码,要他判断这个密码是否是强密码,老师和他说强密码就是需要同时达到以下要求࿱…...
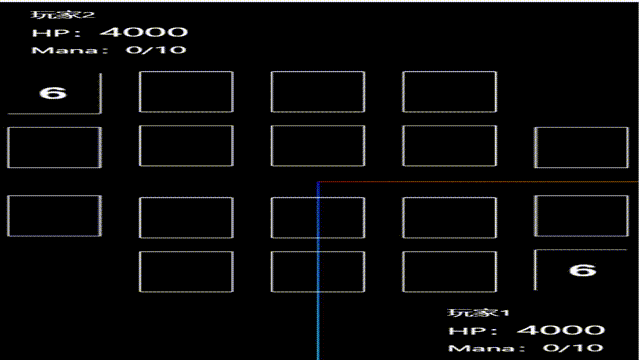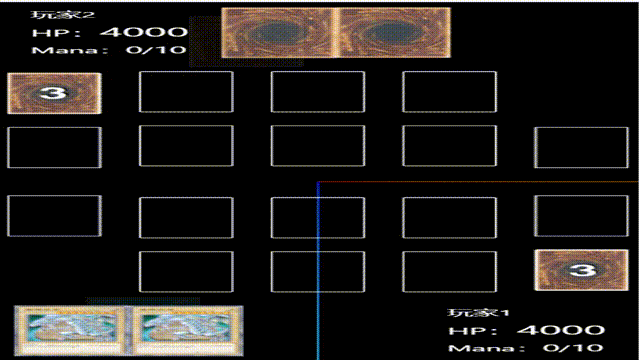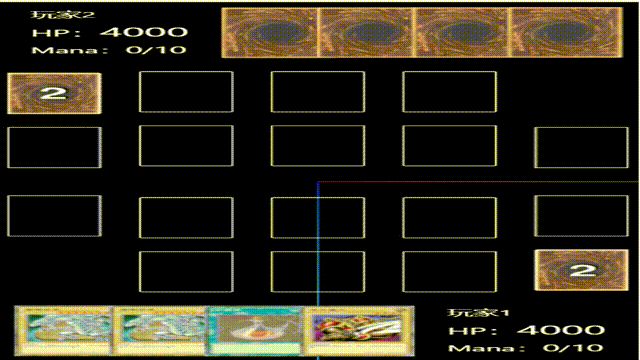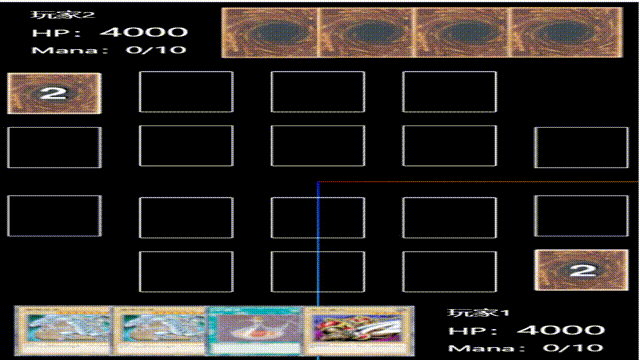
vue3+threejs新手从零开发卡牌游戏(十六):初始化对方手牌
添加对方手牌区时注意位置调整,以及手牌应该是背面朝上,加个rotateX翻转即可,其他代码和p1.vue代码一致,game/hand/p2.vue代码如下: <template><div></div> </template><script setup lan…...
网页无插件视频播放器,支持录像、截图、音视频播放,多路播放等,提供源码下载
前言 本播放器内部采用jessibuca插件接口,支持录像、截图、音视频播放等功能。播放器播放基于ws流,分屏操作支持1分屏、4分屏、6分屏、9分屏方式。 jessibuca工作原理是通过Emscripten将音视频解码库编译成Js(WebAssembly,简称was…...
Openstack创建和操作实例,实现与外部网络通信
一、熟悉OpenStack图形界面操作 1、了解Horizon项目 Horizon项目 各OpenStack服务的图形界面都是由Horizon提供的。Horizon提供基于Web的模块化用户界面。Horizon为云管理员提供一个整体的视图。Horizon为终端用户提供一个自主服务的门户。Horizon由云管理员进行管理与控制&a…...
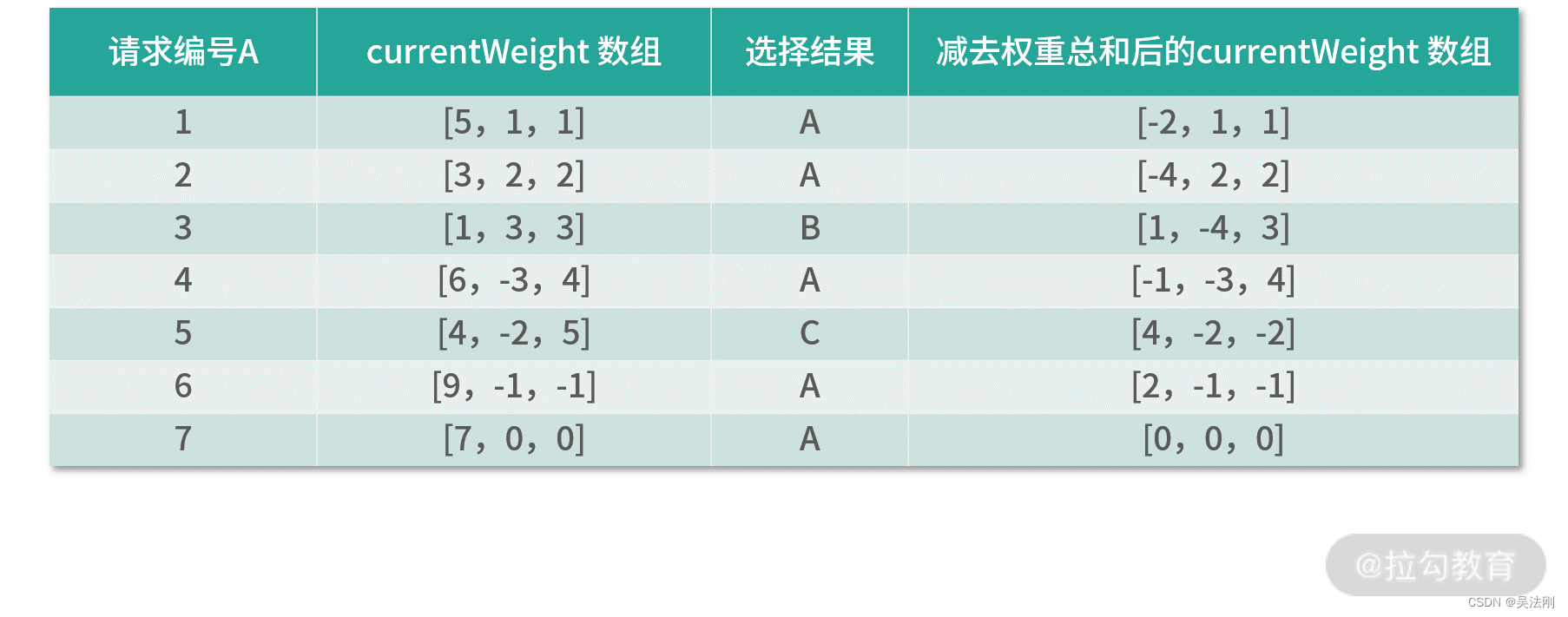
dubbo 源码系列之-集群三板斧---负载均衡(二)
在上一课时我们了解了 LoadBalance 接口定义以及 AbstractLoadBalance 抽象类的内容,还详细介绍了 ConsistentHashLoadBalance 以及 RandomLoadBalance 这两个实现类的核心原理和大致实现。本课时我们将继续介绍 LoadBalance 的剩余三个实现。 LeastActiveLoadBala…...

【一周一篇小题解】洛谷P1035级数求和
还是很简单的…… 首先,输入k,再定义一个双精度浮点数s,不停的循环 for(i1;;i) 每次循环加上1.0/i s1.0/i; 如果大于k就停止循环,并输出,也可以输出后直接结束程序 写法一: if(s>k) { printf("%…...

2024-03-26 AIGC-大模型学习路线
摘要: 2024-03-26 AIGC-大模型学习路线 大模型学习路线 建议先从主流的Llama开始,然后选用中文的Qwen/Baichuan/ChatGLM,先快速上手体验prompt工程,然后再学习其架构,跑微调脚本 如果要深入学习,建议再按以下步骤&am…...
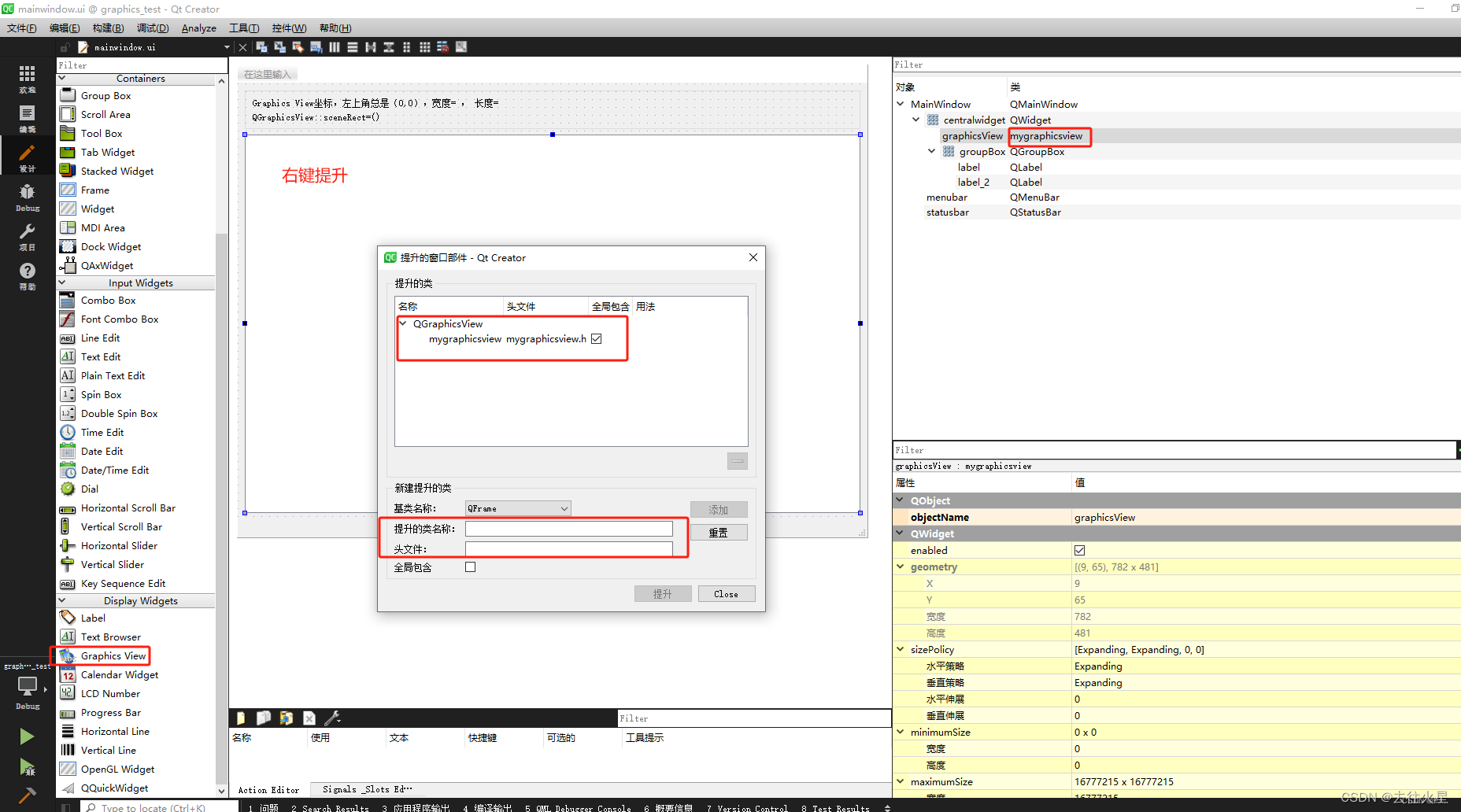
QGraphicsView的使用,view坐标,scene坐标,item坐标
Graphics View绘图构架 QGraphicsScene(场景):可以管理多个图形项QGraphicsItem(图形项):也就是图元,支持鼠标事件响应。QGraphicsView(视图):关联场景可以让…...
from_pretrained 做了啥
transformers的三个核心抽象类是Config, Tokenizer和Model,这些类根据模型种类的不同,派生出一系列的子类。构造这些派生类的对象也很简单,transformers为这三个类都提供了自动类型,即AutoConfig, AutoTokenizer和AutoModel。三个…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...
